Penyelidikan operasi dipacu AI mengoptimumkan 'mesin litografi'! Universiti Sains dan Teknologi China dan lain-lain mencadangkan model jujukan hierarki untuk meningkatkan kecekapan penyelesaian pengaturcaraan matematik.

Penyelesai pengaturcaraan matematik dikenali sebagai "mesin litografi" dalam bidang penyelidikan operasi dan pengoptimuman kerana kepentingan dan serba bolehnya.

Antaranya, Mixed-Integer Linear Programming (MILP) ialah komponen utama penyelesai pengaturcaraan matematik dan boleh memodelkan sejumlah besar aplikasi praktikal, seperti penjadualan pengeluaran industri, penjadualan logistik, reka bentuk cip dan perancangan laluan ., pelaburan kewangan dan bidang utama lain.

Baru-baru ini, pasukan Profesor Wang Jie di Makmal MIRA Universiti Sains dan Teknologi China dan Makmal Bahtera Nuh Huawei telah bersama-sama mencadangkan Model Jujukan Hierarki (HEM), yang meningkatkan kecekapan penyelesaian integer campuran. penyelesai pengaturcaraan linear, dan hasil yang berkaitan telah diterbitkan pada ICLR 2023.

Pada masa ini, algoritma telah disepadukan ke dalam perpustakaan model MindSpore ModelZoo Huawei, dan teknologi serta keupayaan yang berkaitan akan disepadukan ke dalam penyelesai AI OptVerse Huawei tahun ini. Penyelesai ini bertujuan untuk menggabungkan penyelidikan operasi dan AI untuk menembusi had pengoptimuman penyelidikan operasi industri, membantu perusahaan dalam membuat keputusan kuantitatif dan operasi yang diperhalusi, dan mencapai pengurangan kos dan peningkatan kecekapan!

Senarai pengarang: Wang Zhihai*, Li Xijun*, Wang Jie**, Kuang Yufei, Yuan Mingxuan, Zeng Jia, Zhang Yongdong, Wu Feng

Pautan kertas: https://openreview.net/forum?id=Zob4P9bRNcK

Set data sumber terbuka: https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH- Tx3U6hiTJ79sCzxY?usp=sharing

Kod sumber terbuka versi PyTorch: https://github.com/MIRALab-USTC/L2O-HEM-Torch

Kod sumber terbuka versi MindSpore: https:// gitee.com/mindspore/models/ tree/master/research/l2o/hem-learning-to-cut

Penyelesai AI Tianchou (OptVerse): https://www.huaweicloud.com/product/modelarts/ optverse.html

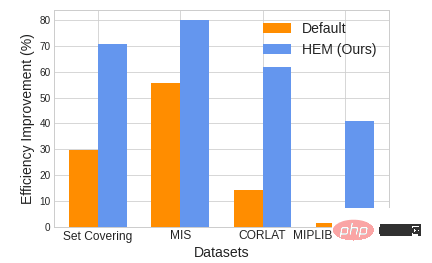
Rajah 1. Perbandingan kecekapan penyelesaian antara HEM dan strategi lalai penyelesai (Lalai kecekapan penyelesaian HEM boleh dipertingkatkan sehingga 47.28%

1 Pengenalan

Pemotongan satah (potongan) adalah penting untuk menyelesaikan masalah pengaturcaraan linear integer campuran dengan cekap.

Antaranya, pemilihan potong (cut selection) bertujuan untuk memilih subset yang sesuai bagi satah potong untuk dipilih bagi meningkatkan kecekapan menyelesaikan MILP. Pemilihan satah pemotongan banyak bergantung pada dua sub-masalah: (P1) satah pemotongan yang manakah harus diutamakan, dan (P2) berapa satah pemotongan harus dipilih.

Walaupun banyak penyelesai MILP moden mengendalikan (P1) dan (P2) dengan heuristik yang direka secara manual, kaedah pembelajaran mesin mempunyai potensi untuk mempelajari heuristik yang lebih cekap.

Walau bagaimanapun, banyak kaedah pembelajaran sedia ada memfokuskan pada pembelajaran satah pemotongan yang harus diutamakan, tetapi abaikan mempelajari bilangan satah pemotongan yang perlu dipilih. Di samping itu, kami telah memerhati daripada sebilangan besar keputusan eksperimen bahawa satu lagi masalah kecil, iaitu (P3), yang memotong susunan satah harus diutamakan, juga mempunyai kesan yang signifikan terhadap kecekapan menyelesaikan MILP.

Untuk menangani cabaran ini, kami mencadangkan Model Jujukan Hierarki (HEM) novel dan mempelajari strategi pemilihan satah pemotongan melalui rangka kerja pembelajaran pengukuhan.

Setahu kita HEM merupakan kaedah pembelajaran pertama yang boleh mengendalikan (P1), (P2) dan (P3) secara serentak. Eksperimen menunjukkan bahawa HEM meningkatkan kecekapan menyelesaikan MILP dengan ketara berbanding garis dasar yang direka dan dipelajari secara manual pada set data MILP dunia sebenar yang dijana secara buatan dan berskala besar.

2 Latar belakang dan pengenalan masalah

2.1 Pengenalan kepada satah pemotongan (potongan)

Mixed-Integer Linear Programming (MILP) ialah model pengoptimuman umum yang digunakan secara meluas dalam pelbagai bidang aplikasi praktikal, seperti pengurusan rantaian bekalan [1], perancangan pengeluaran [2], perancangan dan penghantaran [3], pemilihan lokasi kilang [4], masalah pembungkusan [5], dsb.

MILP standard mempunyai bentuk berikut:

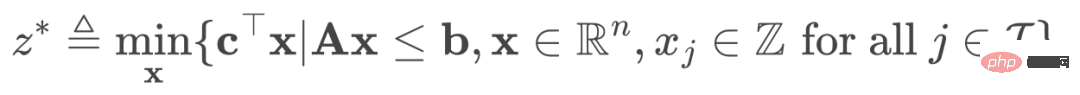
(1)

Masalah yang diberikan ( 1), kami membuang semua kekangan integernya dan mendapatkan masalah kelonggaran pengaturcaraan linear (LPR), yang dalam bentuk:

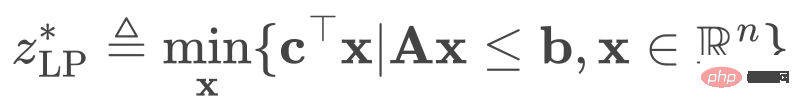
(2)

Memandangkan masalah (2) memanjangkan set masalah yang boleh dilaksanakan (1), kita boleh mempunyai bahawa nilai optimum masalah LPR adalah sempadan bawah masalah MILP asal.

Memandangkan masalah LPR dalam (2), satah pemotongan (potongan) ialah kelas ketaksamaan linear undang-undang yang, apabila ditambah kepada masalah kelonggaran pengaturcaraan linear, mengecilkan kemungkinan ruang domain masalah LPR tanpa mengalih keluar sebarang penyelesaian boleh dilaksanakan integer bagi masalah MILP asal.

2.2 Pengenalan kepada pemilihan potong

Penyelesai MILP boleh menjana sejumlah besar satah pemotong dalam proses menyelesaikan masalah MILP, dan akan terus menambah satah pemotongan kepada masalah asal dalam pusingan berturut-turut.

Secara khusus, setiap pusingan merangkumi lima langkah:

(1) Selesaikan masalah LPR semasa

(2) Hasilkan satu siri satah pemotongan untuk dipilih ;

(3) Pilih subset yang sesuai daripada satah pemotongan untuk dipilih;

(4) Tambahkan subset yang dipilih kepada masalah LPR dalam (1) untuk mendapatkan masalah LPR Baharu;

(5) Kitaran diulang, berdasarkan masalah LPR baharu, dan memasuki pusingan seterusnya.

Menambah semua satah pemotongan yang dijana kepada masalah LPR mengecilkan ruang domain yang boleh dilaksanakan bagi masalah tersebut ke tahap maksimum yang mungkin untuk memaksimumkan sempadan bawah.

Walau bagaimanapun, menambah terlalu banyak satah pemotongan boleh menyebabkan masalah mempunyai terlalu banyak kekangan, meningkatkan overhed pengiraan penyelesaian masalah dan menyebabkan masalah ketidakstabilan berangka [6,7].

Oleh itu, penyelidik telah mencadangkan pemilihan satah pemotongan (cut selection), yang bertujuan untuk memilih subset satah pemotongan calon yang sesuai untuk meningkatkan kecekapan penyelesaian masalah MILP sebanyak mungkin. Pemilihan satah pemotongan adalah penting untuk meningkatkan kecekapan menyelesaikan masalah pengaturcaraan linear integer bercampur [8, 9, 10].

2.3 Percubaan heuristik - tertib penambahan satah pemotongan

Kami mereka bentuk dua algoritma heuristik untuk pemilihan satah memotong, iaitu RandomAll dan RandomNV (lihat Bab 3 kertas asal untuk butiran).

Mereka semua menambah potongan yang dipilih pada masalah MILP dalam susunan rawak selepas memilih kumpulan potongan. Seperti yang ditunjukkan dalam keputusan dalam Rajah 2, apabila satah pemotongan yang sama dipilih, menambah satah pemotongan terpilih ini dalam susunan yang berbeza mempunyai kesan yang besar terhadap kecekapan penyelesaian penyelesai (lihat Bab 3 kertas asal untuk analisis keputusan terperinci).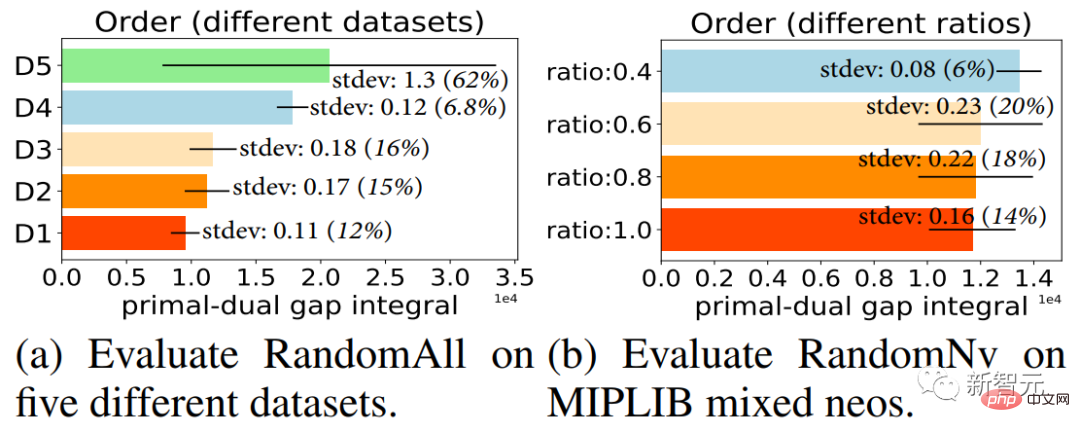

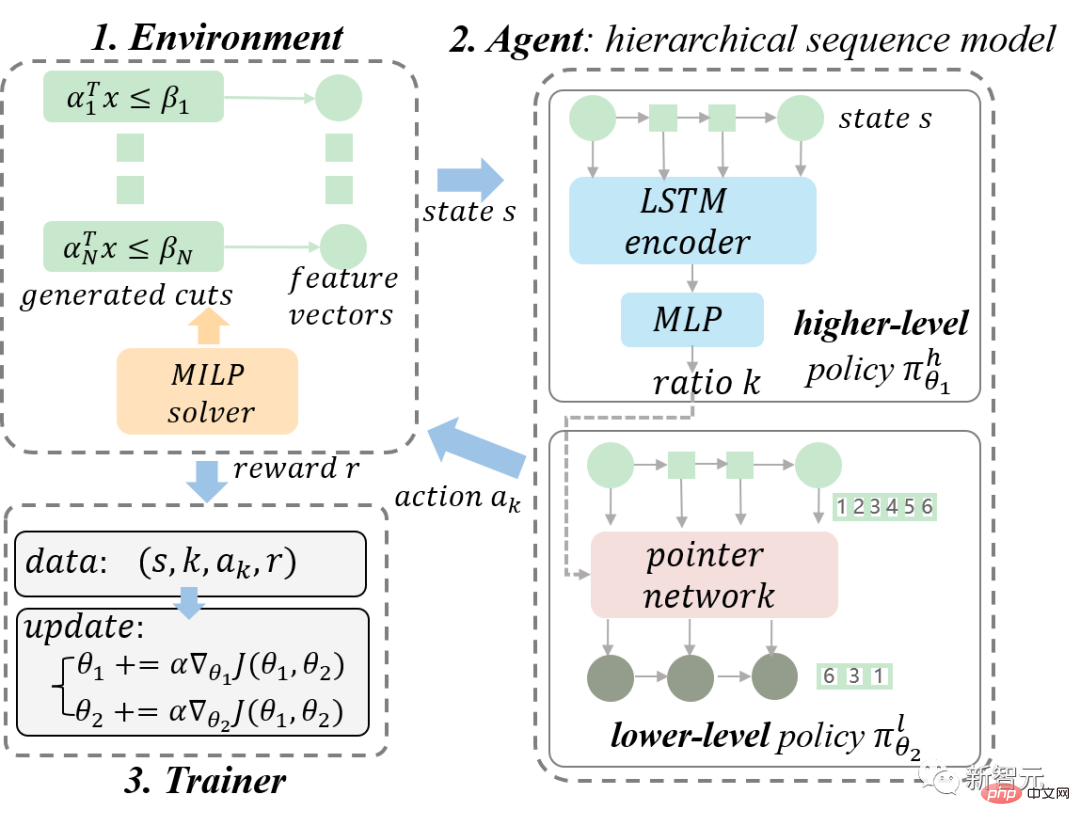
Rajah 2. Setiap lajur mewakili kelompok satah pemotongan yang sama yang dipilih dalam penyelesai, dan ini ditambah dalam 10 susunan berbeza Satah pemotongan adalah dipilih, nilai min kecekapan penyelesaian akhir penyelesai, dan garis sisihan piawai dalam lajur mewakili sisihan piawai kecekapan penyelesaian di bawah susunan yang berbeza. Lebih besar sisihan piawai, lebih besar kesan susunan ke atas kecekapan penyelesaian penyelesai.

3 Pengenalan Kaedah

Dalam tugas pemilihan satah pemotongan, subset optimum yang harus dipilih tidak boleh diperolehi terlebih dahulu.

Walau bagaimanapun, kami boleh menggunakan penyelesai untuk menilai kualiti mana-mana subset yang dipilih dan menggunakan penilaian ini sebagai maklum balas kepada algoritma pembelajaran.

Oleh itu, kami menggunakan paradigma Pembelajaran Pengukuhan (RL) untuk mempelajari strategi pemilihan satah pemotongan melalui percubaan dan kesilapan.

Dalam bahagian ini, kami menghuraikan rangka kerja RL yang dicadangkan kami.

Pertama, kami memodelkan tugas pemilihan satah pemotongan sebagai Proses Keputusan Markov (MDP); kemudian, kami memperkenalkan model jujukan hierarki (HEM) yang dicadangkan secara terperinci Akhirnya, kami memperoleh kecerunan dasar hierarki yang boleh melatih dengan cekap HEM. Gambar rajah rangka kerja RL keseluruhan kami ditunjukkan dalam Rajah 3.

Rajah 3. Gambar rajah rangka kerja RL keseluruhan kami yang dicadangkan. Kami memodelkan penyelesai MILP sebagai persekitaran dan model HEM sebagai ejen. Kami mengumpul data latihan melalui interaksi berterusan antara ejen dan persekitaran, dan melatih model HEM menggunakan kecerunan dasar hierarki.

3.1 Pemodelan Masalah

Ruang negeri: Memandangkan kelonggaran LP semasa dan pemotongan calon yang dijana mengandungi maklumat teras pemilihan satah pemotongan, kami mentakrifkan keadaan. Di sini mewakili model matematik kelonggaran LP semasa, mewakili set satah pemotongan calon, dan mewakili penyelesaian optimum bagi kelonggaran LP. Untuk mengekod maklumat negeri, kami mereka bentuk 13 ciri untuk setiap satah pemotong calon berdasarkan maklumat. Iaitu, kami mewakili keadaan s melalui vektor ciri 13 dimensi. Sila lihat Bab 4 artikel asal untuk butiran khusus.

Ruang tindakan: Untuk mempertimbangkan kedua-dua perkadaran dan susunan pemotongan yang dipilih, kami mentakrifkan ruang tindakan sebagai semua subset tertib bagi set pemotongan calon.

Fungsi ganjaran: Untuk menilai kesan penambahan potongan ke atas penyelesaian MILP, kami boleh menggunakan masa penyelesaian, kamiran jurang primal-dwi dan peningkatan terikat dua. Sila lihat Bab 4 artikel asal untuk butiran khusus.

Fungsi peralihan: Fungsi pemindahan mengeluarkan keadaan seterusnya berdasarkan keadaan semasa dan tindakan yang diambil. Fungsi pemindahan dalam tugas pemilihan satah pemotongan disediakan secara tersirat oleh penyelesai.

Untuk butiran pemodelan lanjut, sila lihat Bab 4 artikel asal.

3.2 Model Strategi: Model Jujukan Hierarki

Seperti yang ditunjukkan dalam Rajah 3, kami memodelkan penyelesai MILP sebagai persekitaran dan HEM sebagai ejen Kaedah yang dicadangkan diperkenalkan secara terperinci di bawah model HEM . Untuk memudahkan pembacaan, kami memudahkan motivasi kaedah dan memberi tumpuan kepada menerangkan dengan jelas pelaksanaan kaedah. Pembaca yang berminat dialu-alukan untuk merujuk Bab 4 kertas asal untuk butiran yang berkaitan.

Seperti yang ditunjukkan dalam modul Ejen dalam Rajah 3, HEM terdiri daripada model dasar atas dan bawah. Model lapisan atas dan bawah masing-masing mempelajari dasar lapisan atas (dasar) dan dasar lapisan bawah.

Pertama, dasar peringkat atas mempelajari bilangan pemotongan yang harus dipilih dengan meramalkan perkadaran yang sesuai. Dengan mengandaikan bahawa panjang keadaan ialah dan nisbah ramalan ialah , maka bilangan potongan yang harus dipilih untuk ramalan ialah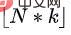

, dengan 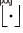mewakili fungsi pembundaran ke bawah. Kami mentakrifkan .

Kedua, dasar peringkat rendah belajar memilih subset tertib bagi saiz tertentu. Dasar peringkat bawah boleh mentakrifkan 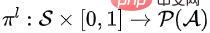, dengan 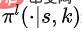mewakili taburan kebarangkalian pada ruang tindakan yang diberi keadaan S dan perkadaran K. Secara khusus, kami memodelkan dasar asas sebagai urutan kepada model jujukan (model jujukan).

Akhir sekali, strategi pemilihan potong diperolehi melalui hukum jumlah kebarangkalian, iaitu

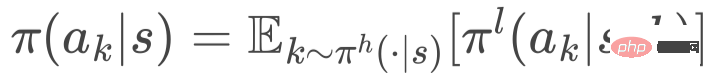
3.3 Kaedah latihan: hierarki kecerunan dasar

Fungsi objektif pengoptimuman yang diberikan

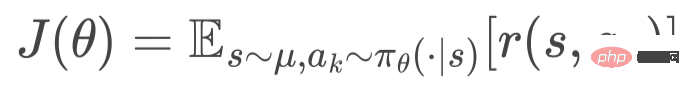
Rajah 4. Kecerunan dasar hierarki. Kami mengoptimumkan model HEM dalam cara penurunan kecerunan stokastik ini.

4 Pengenalan Eksperimen

Eksperimen kami mempunyai lima bahagian utama:

Eksperimen 1. Pada 3 masalah MILP yang dijana secara buatan dan 6 masalah dengan Kaedah kami dinilai pada masalah MILP yang mencabar penanda aras.

Eksperimen 2. Jalankan eksperimen ablasi yang direka dengan teliti untuk memberikan cerapan yang mendalam tentang HEM.

Eksperimen 3. Uji prestasi generalisasi HEM untuk saiz masalah.

Percubaan 4. Visualisasikan ciri-ciri satah pemotongan yang dipilih mengikut kaedah dan garis dasar kami.

Percubaan 5. Gunakan kaedah kami kepada masalah penjadualan pengeluaran sebenar Huawei untuk mengesahkan keunggulan HEM.

Kami hanya memperkenalkan Eksperimen 1 dalam artikel ini Untuk lebih banyak hasil percubaan, sila lihat Bab 5 kertas asal. Sila ambil perhatian bahawa semua keputusan percubaan yang dilaporkan dalam kertas kami adalah keputusan yang diperoleh berdasarkan latihan dengan kod versi PyTorch.

Keputusan Eksperimen 1 ditunjukkan dalam Jadual 1. Kami membandingkan keputusan HEM dan 6 garis dasar pada 9 set data sumber terbuka. Keputusan eksperimen menunjukkan bahawa HEM boleh meningkatkan kecekapan penyelesaian kira-kira 20% secara purata.

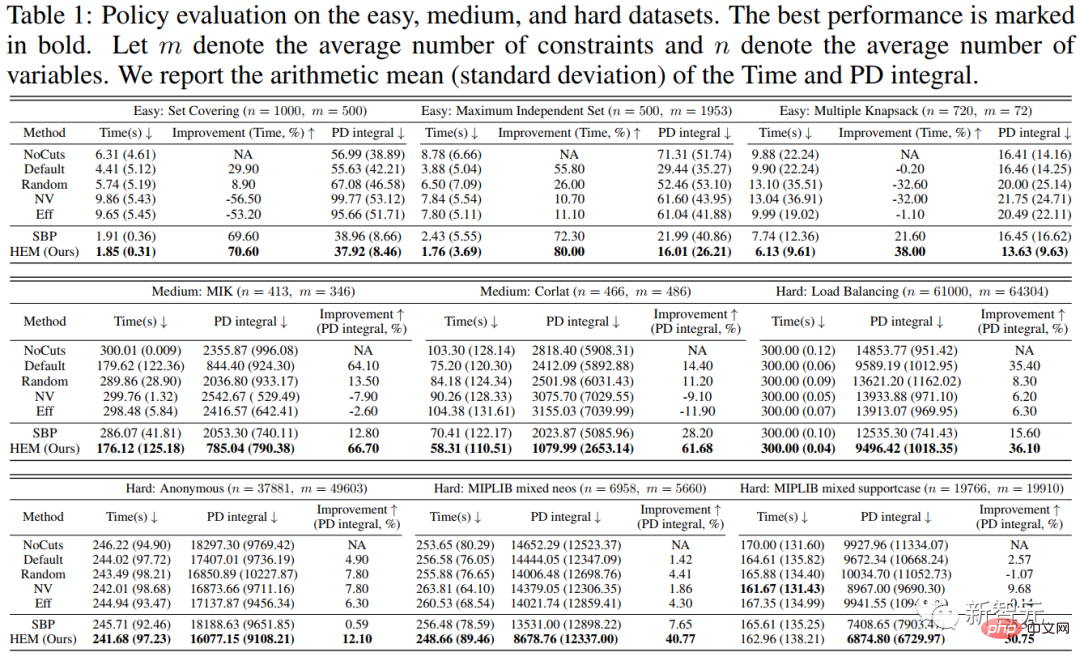
Rajah 5. Penilaian strategi pada set data mudah, sederhana dan keras. Prestasi optimum ditandakan dalam huruf tebal. Biarkan m mewakili purata bilangan kekangan, dan n mewakili purata bilangan pembolehubah. Kami menunjukkan min aritmetik (sisihan piawai) masa penyelesaian dan kamiran jurang primal-dwi.

Atas ialah kandungan terperinci Penyelidikan operasi dipacu AI mengoptimumkan 'mesin litografi'! Universiti Sains dan Teknologi China dan lain-lain mencadangkan model jujukan hierarki untuk meningkatkan kecekapan penyelesaian pengaturcaraan matematik.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!