
Pada 5 Oktober, AlphaTensor telah dilahirkan, dan DeepMind mengumumkan bahawa ia telah menyelesaikan masalah algoritma matematik yang tidak dapat diselesaikan dalam bidang matematik selama 50 tahun, iaitu pendaraban matriks. AlphaTensor menjadi sistem AI pertama yang menemui algoritma baru, cekap dan betul untuk masalah matematik seperti pendaraban matriks. Kertas kerja "Menemui algoritma pendaraban matriks yang lebih pantas dengan pembelajaran pengukuhan" juga muncul pada kulit Alam Semula Jadi.
Walau bagaimanapun, rekod AlphaTensor hanya bertahan selama seminggu sebelum ia dipecahkan oleh ahli matematik manusia.
Dalam karya terbaru mereka, penyelidik Manuel Kauers dan Jakob Moosbauer dari Johann Kepler University Linz, Austria, mengatakan mereka telah memecahkan rekod pendaraban matriks AlphaTensor. Mereka membangunkan kaedah yang melakukan pendaraban matriks 5×5 dalam 95 langkah, kurang satu langkah daripada rekod AlphaTensor sebanyak 96 langkah dan rekod sebelumnya sebanyak 98 langkah. Pracetak kertas itu telah disiarkan di arxiv pada 13 Oktober.

Alamat kertas: https://arxiv.org/abs/2210.04045
"FBHHRBNRSSSHK" dalam tajuk kertas sebenarnya adalah huruf pertama nama akhir semua pengarang kertas DeepMind ini juga sangat menarik:

Penerokaan masalah matematik tidak akan pernah berakhir Seperti yang dikatakan oleh penulis, penyelesaian algoritma DeepMind "masih bukan penghujung cerita". Namun, kejayaan mereka kali ini adalah untuk berdiri di atas bahu gergasi, iaitu AI Penulis berkata bahawa penyelesaian mereka adalah untuk menerapkan satu siri transformasi berdasarkan penyelesaian DeepMind untuk menghapuskan pendaraban satu langkah. pengiraan.
Mari kita semak secara ringkas keputusan AlphaTensor.
Banyak tugasan matematik dalam sains komputer dikendalikan melalui pendaraban matriks, seperti pembelajaran mesin, penciptaan grafik komputer, pelbagai simulasi atau pemampatan data. Komputer mengira pendaraban jauh lebih perlahan daripada penambahan, jadi walaupun peningkatan kecil dalam kecekapan pendaraban matriks boleh memberi impak yang besar Selama beberapa dekad, ahli matematik telah mencari algoritma pendaraban matriks yang lebih cekap.
Pada tahun 1969, ahli matematik Jerman Volker Strassen membangunkan algoritma yang buat pertama kalinya mengurangkan penyelesaian pendaraban matriks 4×4 daripada 64 langkah kepada 49 langkah, mengejutkan dunia matematik.
Sistem AI AlphaTensor yang dikeluarkan oleh Deepmind kali ini menemui algoritma baharu yang lebih pantas daripada algoritma Strassen. Demis Hassabis berkata algoritma baharu itu berpotensi meningkatkan kecekapan sebanyak 10% hingga 20% dalam trilion pengiraan setiap hari.
AlphaTensor ialah lonjakan daripada permainan kepada matematik, berdasarkan AlphaZero, sistem AI permainan papan tujuan umum yang dikeluarkan oleh Deepmind pada 2018. Untuk melatih AlphaTensor, pasukan penyelidik Deepmind mengubah masalah pendaraban matriks menjadi permainan papan 3D, dengan setiap langkah menghasilkan blok binaan algoritma baharu. AlphaTensor diberi ganjaran kerana menjana algoritma baharu dalam beberapa langkah yang mungkin dengan memilih antara berpuluh-puluh ribu pergerakan setiap kali. Deepmind memanggil ini sebagai "permainan tensor."
Dalam matriks input 5×5, AlphaTensor secara bebas menemui algoritma Strassen dan algoritma lain yang diketahui. Selain itu, ia telah membangunkan algoritma baharu yang lebih cekap daripada yang lama.
Sebagai contoh, pendaraban matriks 5×5 (n=4) sebelum ini memerlukan 80 langkah pengiraan, tetapi algoritma baharu AlphaTensor hanya memerlukan 76 langkah apabila n=5, AlphaTensor akan menyelesaikan masalah daripada 98 langkah asal dikurangkan kepada 96 langkah. Pendaraban matriks 4×4 dikurangkan kepada 49 langkah oleh Strassen dan dioptimumkan kepada 47 langkah oleh AlphaTensor. Kecekapan ini dicapai dengan lebih daripada 70 algoritma untuk pendaraban matriks yang dijana oleh AlphaTensor.
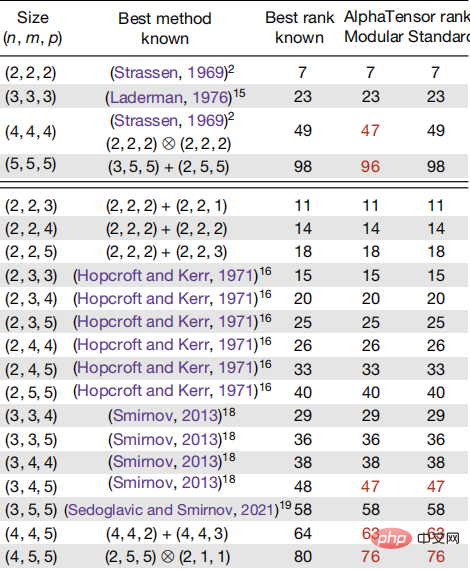
Kapsyen: Perbandingan kerumitan algoritma yang ditemui oleh AlphaTensor dengan algoritma pendaraban matriks yang diketahui
Selain itu, AlphaTensor juga boleh membangunkan algoritma khusus perkakasan , untuk pembelajaran mesin. Ia dikatakan pada masa ini berjalan 20% lebih pantas daripada algoritma pada Google TPU dan NVIDIA V100s.
Sukar bagi manusia untuk melaraskan algoritma pendaraban secara autonomi untuk menyesuaikan diri dengan perkakasan, jadi penambahbaikan AlphaTensor bagi algoritma Strassen mencipta had atas baharu untuk pendaraban matriks 4×4, iaitu kemajuan AI. Satu bukti besar kepada bantuan yang diberikan oleh disiplin lain. Ia juga menunjukkan bahawa sistem AlphaZero, yang pada asalnya dibangunkan untuk permainan tradisional, boleh menyelesaikan masalah matematik di luar domain.
Dalam penyelidikan terbaru oleh Manuel Kauers dan Jakob Moosbauer, mereka terutamanya membuat dua penemuan baharu, Pertama, untuk matriks 4×4, mereka mencadangkan satu lagi algoritma penyelesaian pendaraban 47 langkah, tetapi ia berbeza daripada penyelesaian sebelumnya, untuk matriks 5×5, mereka mencadangkan penyelesaian yang memerlukan 95 langkah pendaraban untuk kali pertama;
Dalam artikel ini, penulis menunjukkan secara ringkas dua skema pendaraban matriks Satu kertas rasmi akan diterbitkan tidak lama lagi untuk memperkenalkan teknologi carian algoritma penyelesaian dengan lebih terperinci.
Skim baharu untuk matriks 4 × 4 mengandungi sejumlah 47 pendaraban, seperti berikut:
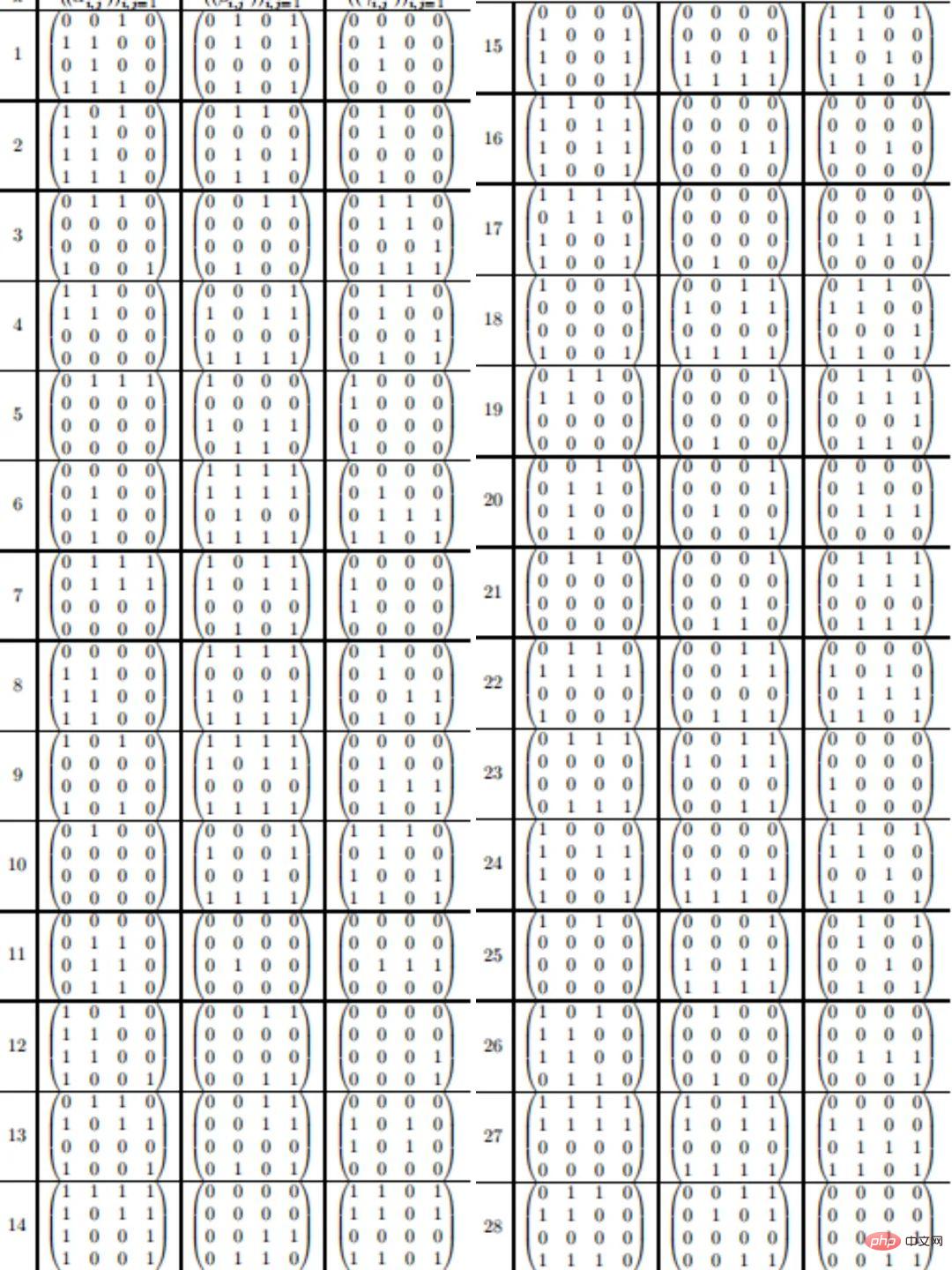
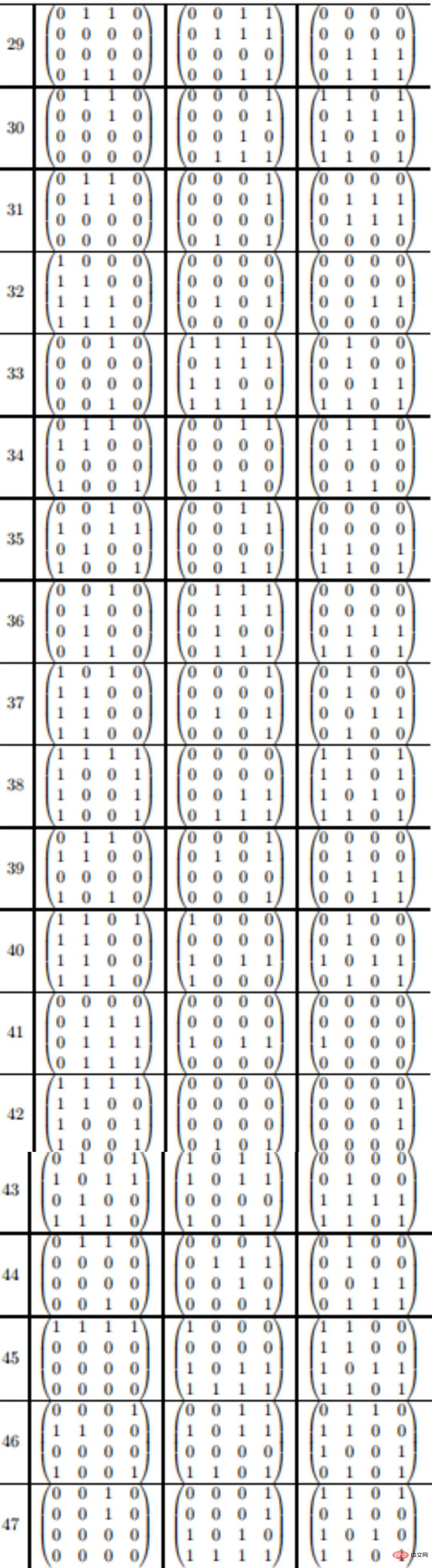
5 Skim pendaraban 95 langkah untuk >
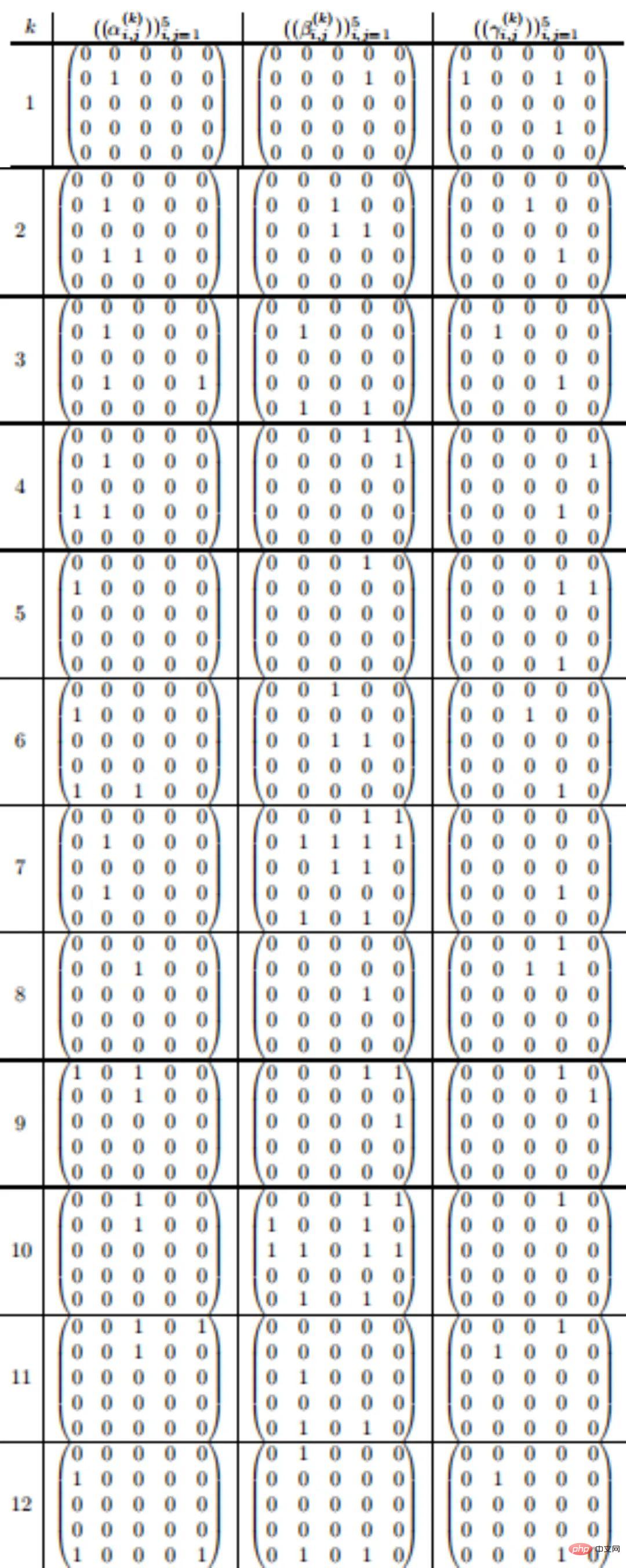 Memandangkan GPU melakukan trilion pengiraan matriks setiap hari, jadi daripada 98 langkah kepada 96 langkah dan daripada 96 langkah Peningkatan tambahan yang kelihatan kecil seperti langkah 95 sebenarnya boleh meningkatkan kecekapan pengiraan dan membolehkan aplikasi AI berjalan lebih pantas pada perkakasan sedia ada.
Memandangkan GPU melakukan trilion pengiraan matriks setiap hari, jadi daripada 98 langkah kepada 96 langkah dan daripada 96 langkah Peningkatan tambahan yang kelihatan kecil seperti langkah 95 sebenarnya boleh meningkatkan kecekapan pengiraan dan membolehkan aplikasi AI berjalan lebih pantas pada perkakasan sedia ada.
Manuel Kauers, profesor algebra di Universiti Johannes Kepler di Linz, ketua Institut Algebra orang universiti. Minat penyelidikannya ialah algebra komputer, penjumlahan dan penyepaduan simbolik, identiti fungsi khas, dsb.
Jakob Moosbauer, pelajar PhD di Institut Algebra, Universiti Johannes Kepler Linz.
Atas ialah kandungan terperinci Manusia mengatasi AI: Seminggu selepas DeepMind menggunakan AI untuk memecahkan rekod 50 tahun untuk kelajuan pengiraan darab matriks, ahli matematik memecahkannya sekali lagi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




