
Sejak kebelakangan ini, lukisan AI sangat popular.
Semasa anda mengagumi keupayaan lukisan AI, perkara yang anda mungkin tidak tahu ialah model resapan memainkan peranan yang besar di dalamnya. Ambil model OpenAI's DALL·E 2 sebagai contoh Hanya masukkan teks ringkas (prompt) dan ia boleh menjana berbilang imej definisi tinggi 1024*1024.
Tidak lama selepas DALL·E 2 diumumkan, Google kemudiannya mengeluarkan Imagen, model AI teks-ke-imej yang boleh menjana imej realistik pemandangan daripada imej teks yang diberikan .
Hanya beberapa hari yang lalu, Stability.Ai mengeluarkan versi terkini Stable Diffusion secara terbuka, model imej penjanaan teks dan imej yang dijananya mencapai gred komersial.
Sejak Google mengeluarkan DDPM pada 2020, model resapan telah beransur-ansur menjadi tempat hangat baharu dalam bidang penjanaan. Kemudian, OpenAI melancarkan model GLIDE, ADM-G, dsb., yang menjadikan model penyebaran popular.
Ramai penyelidik percaya bahawa model penjanaan imej teks berdasarkan model resapan bukan sahaja mempunyai bilangan parameter yang kecil, tetapi juga menjana imej berkualiti tinggi, dan berpotensi untuk menggantikan GAN.
Walau bagaimanapun, formula matematik di sebalik model resapan telah menggerunkan ramai penyelidik, dan ramai penyelidik percaya bahawa ia adalah lebih sukar untuk difahami berbanding VAE dan GAN.
Baru-baru ini, penyelidik dari Penyelidikan Google menulis "Memahami Model Penyebaran: Perspektif Bersepadu" Artikel ini menunjukkan prinsip matematik di sebalik model resapan dengan cara yang sangat terperinci, dengan tujuan membenarkan orang lain. Penyelidik boleh mengikuti dan mempelajari model resapan dan cara ia berfungsi. 
Alamat kertas: https://arxiv.org/pdf/2208.11970.pdf Mengenai bagaimana "matematik" kertas ini, penulis menerangkannya seperti ini : Kami menunjukkan matematik di sebalik model ini dengan terperinci yang menyiksa.
Kertas ini dibahagikan kepada 6 bahagian, terutamanya termasuk model generatif ELBO, VAE dan hierarki model resapan variasi;

Berikut ialah petikan daripada kertas untuk pengenalan:
Memandangkan sampel pemerhatian x dalam taburan, matlamat model generatif adalah untuk belajar memodelkan taburan data sebenar p(x). Selepas model dipelajari, kita boleh menjana sampel baharu. Selain itu, dalam beberapa bentuk, kita juga boleh menggunakan model pembelajaran untuk menilai pemerhatian atau data sampel.
Dalam literatur penyelidikan semasa, terdapat beberapa arahan penting Artikel ini hanya memperkenalkan secara ringkasnya pada tahap yang tinggi, terutamanya termasuk: GAN, yang memodelkan proses pensampelan Learn secara bermusuhan. Model generatif, yang juga boleh kita panggil kaedah "berasaskan kemungkinan", boleh menetapkan kemungkinan tinggi kepada sampel data yang diperhatikan dan biasanya termasuk autoregresi, aliran normal dan VAE. Pemodelan berasaskan tenaga, dalam pendekatan ini, pengagihan dipelajari sebagai fungsi tenaga fleksibel sewenang-wenangnya dan kemudian dinormalisasi. Dalam model generatif berasaskan skor, bukannya belajar memodelkan fungsi tenaga itu sendiri, skor berdasarkan model tenaga dipelajari sebagai rangkaian saraf.
Dalam kajian ini, kertas kerja ini meneroka dan mengkaji model resapan, seperti yang ditunjukkan dalam kertas kerja, mereka mempunyai tafsiran berasaskan kemungkinan dan berasaskan skor.
Dalam istilah mudah, Model Resapan Variasi (VDM) boleh dianggap sebagai mempunyai tiga Pengekod Variasi Hierarki Markov (atau diandaikan) utama ( MHVAE), mereka ialah:
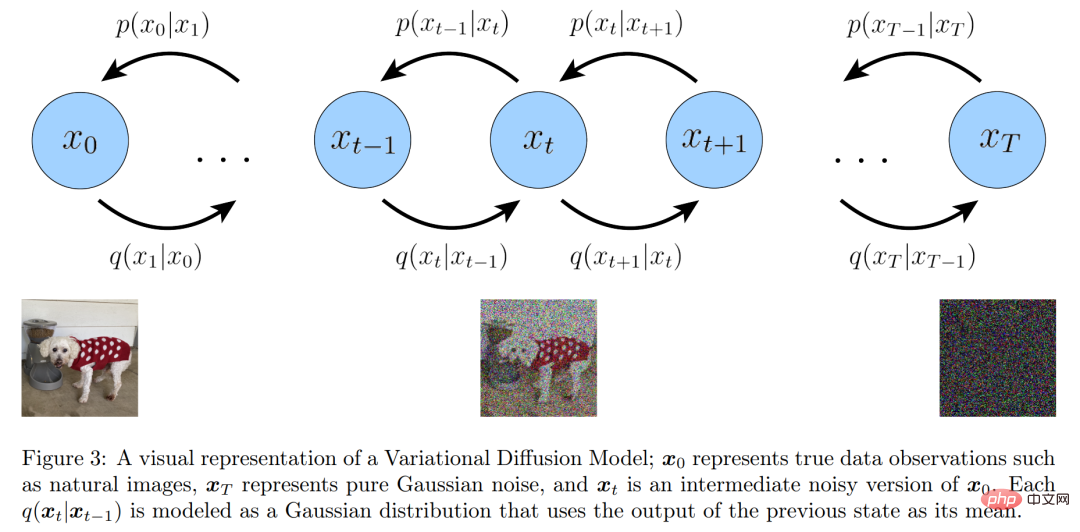
Bermula dari andaian pertama, disebabkan penyalahgunaan simbol, sampel data sebenar dan pembolehubah pendam kini boleh diwakili sebagai x_t, di mana t=0 mewakili data sampel sebenar, t ∈ [1 , T] mewakili pembolehubah pendam yang sepadan, dan struktur hierarkinya diindeks oleh t. Posterior VDM adalah sama dengan posterior MHVAE, tetapi kini boleh ditulis semula seperti berikut:
Daripada hipotesis kedua , Adalah diketahui bahawa taburan setiap pembolehubah terpendam dalam pengekod adalah taburan Gaussian yang berpusat pada pembolehubah pendam hierarki sebelum ini. Berbeza daripada MHVAE, struktur pengekod pada setiap langkah masa tidak dipelajari, ia ditetapkan sebagai model Gaussian linear, di mana min dan sisihan piawai boleh dipratetap sebagai hiperparameter atau dipelajari sebagai parameter. Secara matematik, transformasi pengekod dinyatakan seperti berikut:

Untuk hipotesis ketiga, α_t adalah tetap atau boleh dipelajari mengikut The jadual yang diperolehi berkembang dari semasa ke semasa, supaya taburan pembolehubah pendam akhir p(x_T) ialah taburan Gaussian standard. Pengedaran bersama MHVAE kemudiannya boleh dikemas kini dan pengedaran bersama VDM boleh ditulis seperti berikut:
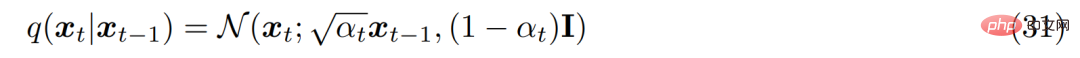
Dalam ringkasan, Satu siri andaian ini menerangkan bunyi stabil imej apabila ia berkembang dari semasa ke semasa. Para penyelidik secara beransur-ansur merosakkan imej dengan menambah hingar Gaussian sehingga akhirnya menjadi sama dengan hingar Gaussian.
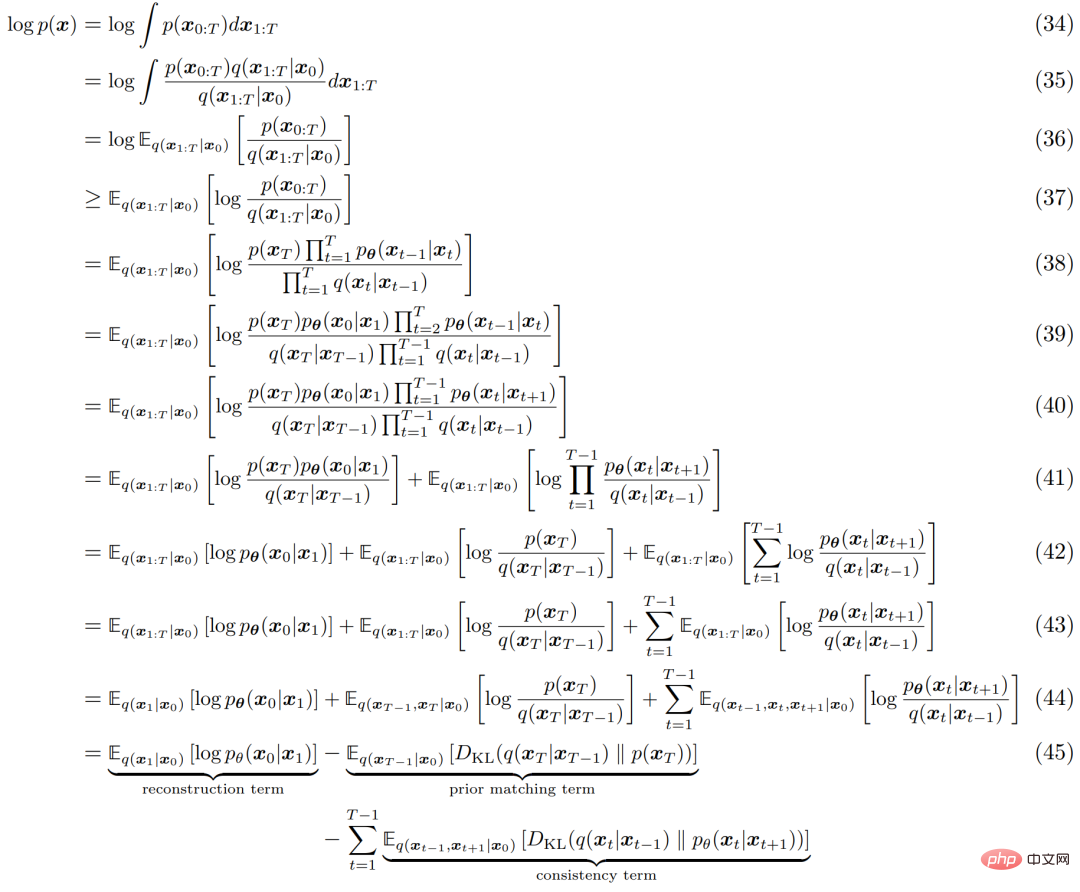
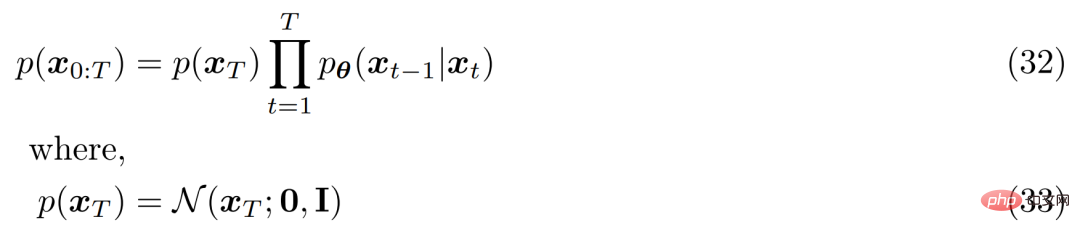 Sama seperti mana-mana HVACE, VDM boleh dioptimumkan dengan memaksimumkan Evidence Lower Bound (ELBO), yang boleh diperoleh seperti berikut:
Sama seperti mana-mana HVACE, VDM boleh dioptimumkan dengan memaksimumkan Evidence Lower Bound (ELBO), yang boleh diperoleh seperti berikut:
Proses tafsiran ELBO ditunjukkan dalam Rajah 4 di bawah:
Tiga penjelasan yang setara
Seperti yang ditunjukkan sebelum ini, model resapan variasi boleh dilatih hanya dengan mempelajari rangkaian saraf untuk meramalkan asal daripada versi x_t yang bising sewenang-wenangnya dan indeks masanya t Imej semula jadi x_0. Walau bagaimanapun, terdapat dua parameterisasi yang setara bagi x_0, membenarkan dua tafsiran lanjut VDM dibangunkan. 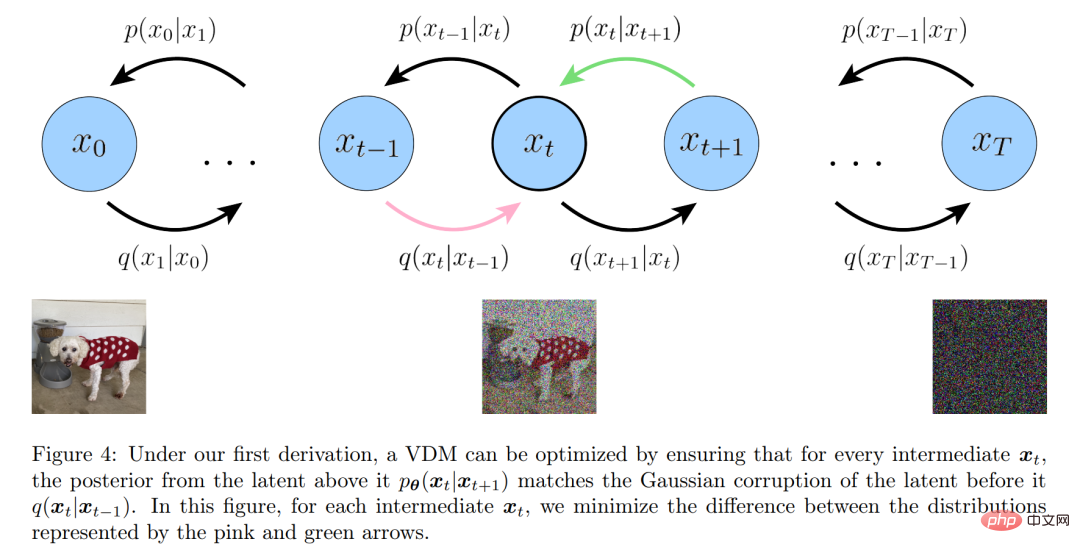
Bawa ia ke dalam min transformasi denoising sebenar yang diperoleh sebelum ini µ_q(x_t, x_0), anda boleh mendapatkannya semula seperti berikut: 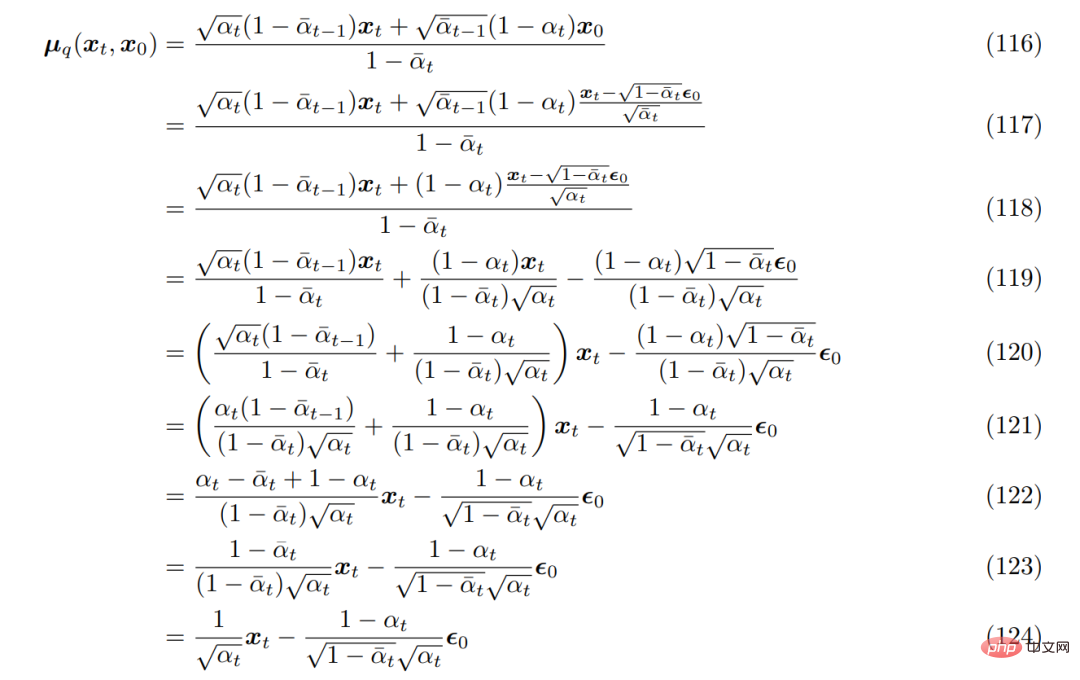
Oleh itu anda boleh Anggaran penyahnoikan yang diubah min µ_θ(x_t, t) ditetapkan seperti berikut:
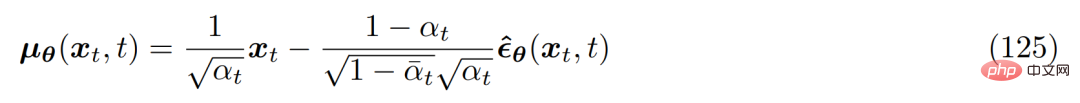
dan masalah pengoptimuman yang sepadan menjadi seperti berikut :
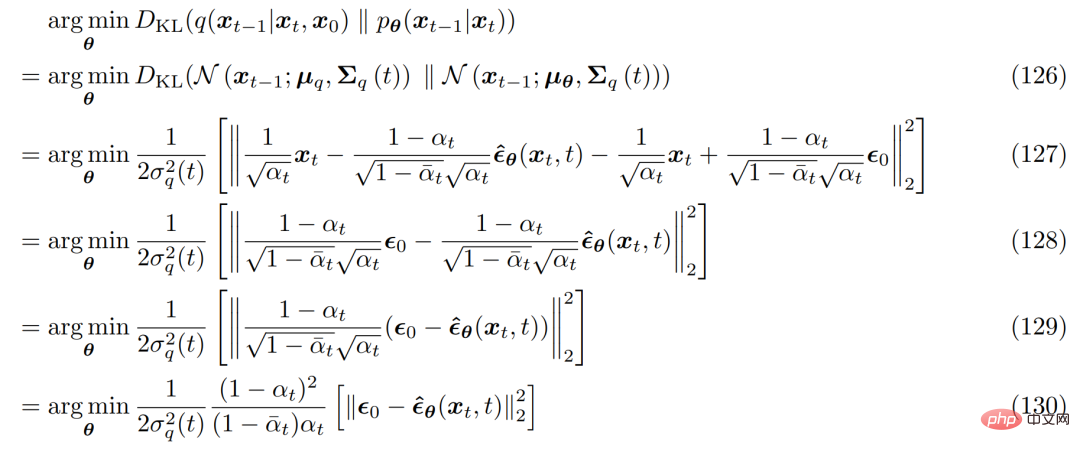
Untuk mendapatkan tiga tafsiran biasa model resapan variasi, seseorang perlu beralih kepada formula Tweedie , yang merujuk kepada ialah apabila sampel diberikan, min sebenar taburan keluarga eksponen boleh dianggarkan dengan anggaran kemungkinan maksimum sampel (juga dipanggil min empirikal) ditambah beberapa istilah pembetulan yang melibatkan skor anggaran.
Secara matematik, untuk pembolehubah Gaussian z ∼ N (z; µ_z, Σ_z), formula Tweedie dinyatakan seperti berikut:
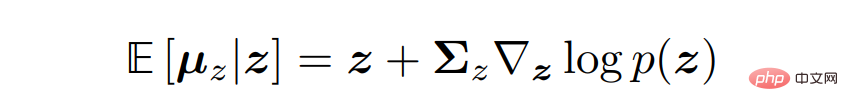
Penyelidik telah menunjukkan bahawa model resapan variasi boleh dipelajari hanya dengan mengoptimumkan rangkaian saraf s_θ(x_t, t) diperolehi untuk meramal fungsi skor ∇ log p(x_t). Walau bagaimanapun, istilah pemarkahan dalam terbitan berasal daripada penggunaan formula Tweedie. Ini tidak semestinya memberikan intuisi yang baik atau cerapan tentang apakah sebenarnya fungsi skor atau mengapa ia patut dimodelkan.
Mujurlah intuisi ini boleh diperolehi dengan bantuan model generatif jenis lain iaitu model generatif berasaskan skor. Para penyelidik sememangnya menunjukkan bahawa rumusan VDM yang diperoleh sebelum ini mempunyai rumusan pemodelan generatif berasaskan pecahan yang setara, membolehkan penukaran fleksibel antara kedua-dua tafsiran.
Untuk memahami sebab mengoptimumkan fungsi skor masuk akal, penyelidik menyemak semula model berasaskan tenaga. Taburan kebarangkalian fleksibel arbitrari boleh ditulis dalam bentuk berikut: Kaedahnya adalah dengan menggunakan rangkaian saraf s_θ(x) untuk mempelajari fungsi skor ∇ log p(x) taburan p(x). Adalah diperhatikan bahawa kedua-dua belah Persamaan 152 boleh dibezakan secara logaritma:

yang boleh dinyatakan secara bebas sebagai saraf rangkaian , tidak melibatkan sebarang pemalar normalisasi. Fungsi skor boleh dioptimumkan dengan meminimumkan perbezaan Fisher menggunakan fungsi skor sebenar.
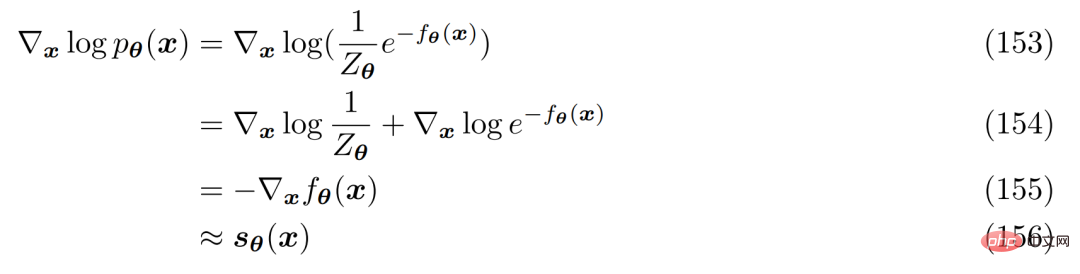
Secara intuitif, fungsi skor mentakrifkan medan vektor di seluruh ruang tempat data x terletak dan titik kepada Model ditunjukkan dalam Rajah 6 di bawah.

Akhir sekali, penyelidik menubuhkan model resapan variasi dan berasaskan skor Menjana perkaitan eksplisit antara model.
Sila rujuk kertas asal untuk butiran lanjut. 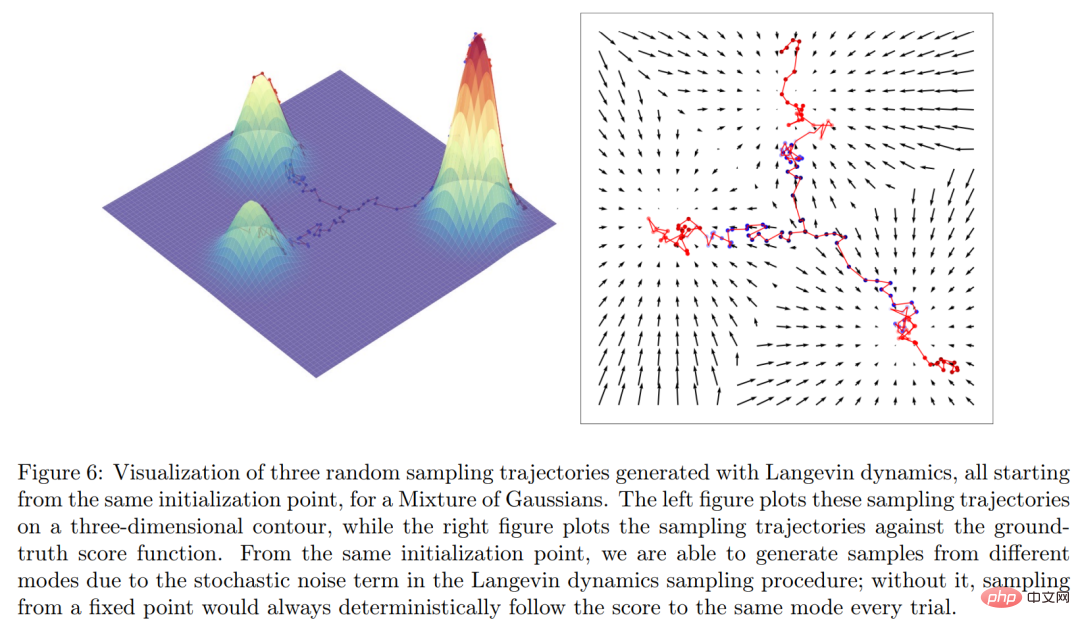
Atas ialah kandungan terperinci Adakah matematik di sebalik model resapan terlalu sukar untuk dihadam? Google menjelaskannya dengan perspektif yang bersatu. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




