 Peranti teknologi
Peranti teknologi
 AI
AI
 Rangkaian saraf graf telah diterbitkan dalam sub-jurnal Alam, tetapi ia telah didedahkan bahawa ia adalah 104 kali lebih perlahan daripada algoritma biasa Penanya: Adakah ia ketinggian baru?
Rangkaian saraf graf telah diterbitkan dalam sub-jurnal Alam, tetapi ia telah didedahkan bahawa ia adalah 104 kali lebih perlahan daripada algoritma biasa Penanya: Adakah ia ketinggian baru?
Rangkaian saraf graf telah diterbitkan dalam sub-jurnal Alam, tetapi ia telah didedahkan bahawa ia adalah 104 kali lebih perlahan daripada algoritma biasa Penanya: Adakah ia ketinggian baru?
GNN ialah bidang yang sangat popular sejak beberapa tahun kebelakangan ini. Baru-baru ini, kertas sub-jurnal Nature mencadangkan kaedah untuk menggunakan GNN untuk menyelesaikan masalah pengoptimuman gabungan, dan mendakwa bahawa prestasi pengoptimum GNN adalah setara atau bahkan melebihi penyelesai sedia ada. Walau bagaimanapun, kertas kerja ini telah menarik beberapa keraguan: sesetengah orang menunjukkan bahawa prestasi GNN ini sebenarnya tidak sebaik algoritma tamak klasik, dan kelajuannya jauh lebih perlahan daripada algoritma tamak (untuk masalah dengan satu juta pembolehubah, tamak algoritma adalah lebih baik daripada GNN 104 kali lebih pantas). Oleh itu, orang yang ragu-ragu berkata, "Kami tidak melihat sebarang alasan yang baik untuk menggunakan GNN ini untuk menyelesaikan masalah ini, ia seperti menggunakan tukul besi untuk memecahkan kacang." keunggulan kaedah tersebut.
Dalam beberapa tahun kebelakangan ini, rangkaian saraf telah menyelesaikan banyak masalah sukar dalam aplikasi dan sains asas, termasuk masalah pengoptimuman gabungan diskret, yang juga merupakan asas untuk pemahaman kita tentang had pengkomputeran.
Kajian 2022 Martin JA Schuetz et al. "Pengoptimuman gabungan dengan rangkaian saraf graf yang diilhamkan fizik" [4] dicadangkan untuk menggunakan rangkaian neural graf tanpa pengawasan (GNN) yang diilhamkan oleh fizik untuk Pendekatan ini nampaknya menjanjikan untuk menyelesaikan masalah pengoptimuman gabungan pada graf dan telah diterbitkan dalam jurnal berimpak tinggi (Nature Machine Intelligence). Kajian itu menguji prestasi GNN pada dua masalah pengoptimuman standard: potongan maksimum dan set bebas maksimum (MIS). Pengoptimum GNN yang baru dicadangkan ini mempunyai sifat yang sangat bagus: ia boleh diperluaskan kepada banyak masalah contoh yang lebih besar.

Alamat kertas: https://arxiv.org/pdf/2107.01188.pdf
Walau bagaimanapun, kertas baru baru-baru ini "Memecahkan kacang dengan tukul besi: apabila rangkaian saraf graf moden lebih teruk daripada algoritma tamak klasik" telah mempersoalkan penyelidikan Martin JA Schuetz et al., dengan alasan bahawa Martin JA Schuetz et al. Pengoptimum GNN ialah "memecahkan kacang dengan tukul besi, sama seperti memukul nyamuk dengan mortar", yang membazir sumber dan mempunyai hasil yang buruk.

Alamat kertas: https://arxiv.org/abs/2206.13211
Masalah MIS ditakrifkan seperti berikut: Memandangkan graf biasa rawak tidak terarah (d-RRG) dengan n nod dan darjah ditetapkan kepada d, set bebas (IS) merujuk kepada subset bucu yang tidak mengandungi jiran terdekat. pasangan ; Masalah MIS memerlukan mencari IS terbesar, yang saiznya dipanggil α. MIS ialah masalah NP-hard, tetapi seseorang ingin mencari algoritma untuk mencari IS dengan saiz sehampir mungkin kepada maksimum dalam masa polinomial. Tambahan pula, algoritma yang baik tidak seharusnya mengalami kemerosotan prestasi untuk nilai n yang lebih besar.
GNN baharu yang dicadangkan oleh Martin JA Schuetz et al boleh mencari IS untuk graf yang sangat besar (n≤ 10^6): masa berjalan algoritma adalah berkadar dengan saiz masalah: t. ∼ n^ 1.7, dan prestasi algoritma kekal stabil apabila n meningkat, seperti ditunjukkan dalam Rajah 1 di bawah.
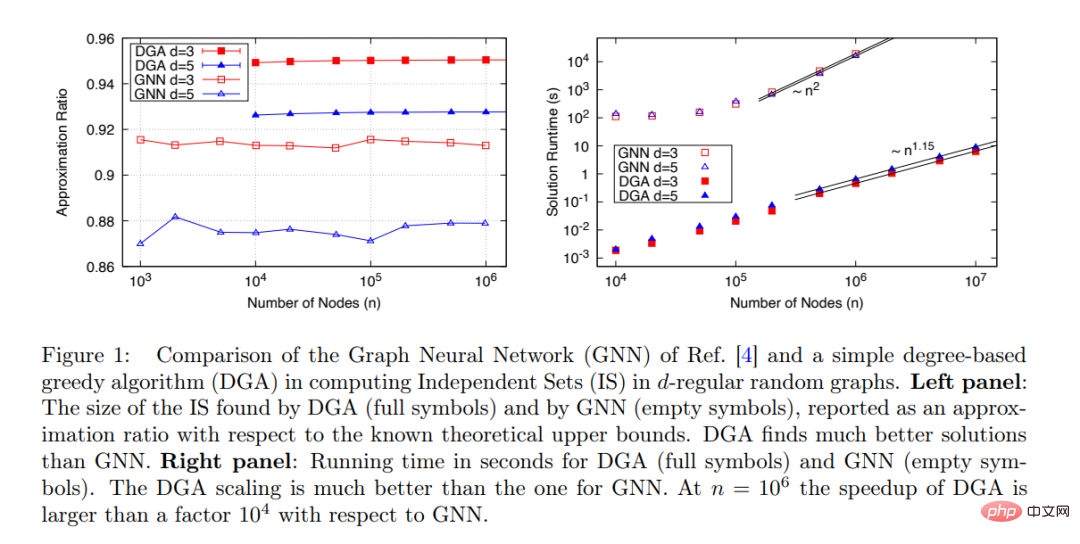
Walau bagaimanapun, apabila membandingkan prestasi GNN yang dicadangkan dengan algoritma lain yang tersedia, kajian ini hanya membandingkan dengan Boppana- Algoritma penghampiran Halldorsson (BH) [8] telah dibandingkan Apabila n≤500, algoritma ini mempunyai masa berjalan t∼n^2.9.
Sebenarnya terdapat banyak algoritma lain untuk mengira IS yang jauh lebih pantas daripada BH, dan kajian itu harus membandingkan pengoptimum GNN yang dicadangkan dengan algoritma ini. Antaranya, algoritma yang paling mudah ialah algoritma tamak (GA) [9]. Selepas algoritma tamak berasaskan darjah (DGA) dioptimumkan, masa berjalan adalah hampir linear dengan bilangan nod n.
Kajian ini membandingkan pengoptimum GNN (terbuka) dan DGA (pepejal) yang dicadangkan oleh Martin JA Schuetz et al untuk mencari MIS pada d-RRG dengan d=3 dan d=5 prestasi. Seperti yang ditunjukkan dalam Rajah 1 (kanan), dari hubungan antara masa berjalan dan saiz masalah (bilangan nod), DGA jauh lebih baik daripada GNN Masa berjalan yang pertama adalah hampir berkadar dengan bilangan nod n. Terdapat hubungan linear (eksponen ialah 1.15 mungkin disebabkan oleh kesan pra-asimptotik), manakala masa berjalan GNN mempunyai hubungan hampir kuadratik dengan bilangan nod n.
Kajian ini percaya bahawa dakwaan Martin JA Schuetz et al. bahawa "prestasi pengoptimum berdasarkan rangkaian saraf graf adalah bersamaan atau lebih baik daripada penyelesai sedia ada, dan mempunyai keupayaan untuk mengatasi model SOTA semasa. "Boleh diperluaskan kepada masalah dengan berjuta-juta pembolehubah" tidak dapat menahan penelitian dan tidak konsisten dengan keputusan percubaan sebenar Martin JA Schuetz dan yang lain harus menyemak kertas itu.
Kajian ini menghuraikan prestasi DGA dan percaya bahawa algoritma tamak mudah ini harus dianggap sebagai penanda aras minimum, dan prestasi mana-mana algoritma baharu mestilah sekurang-kurangnya lebih baik daripada DGA Bakat yang baik diterima pakai.
Sudah tentu, DGA hanyalah algoritma yang sangat mudah, dan terdapat banyak algoritma standard lain yang lebih baik daripada DGA. Makalah 2019 Maria Chiara et al. "Algoritma Monte carlo sangat berkesan dalam mencari set bebas terbesar dalam graf rawak jarang" menyediakan kajian mendalam tentang prestasi berbilang algoritma untuk menyelesaikan masalah MIS.
Berdasarkan perkara ini, kajian ini menimbulkan persoalan: "Apabila menilai algoritma pengoptimuman baharu, apakah masalah yang benar-benar sukar yang harus digunakan sebagai penanda aras untuk menguji prestasi algoritma?"
Sebagai contoh, kajian ini percaya bahawa MIS pada d-RRG d16. Di sini keputusan untuk d=20 dan d=100 boleh dibandingkan dengan keputusan yang diberikan dalam kertas 2019 "Algoritma Monte carlo sangat berkesan dalam mencari set bebas terbesar dalam graf rawak jarang".
Jelas sekali, algoritma pengoptimuman yang baik harus diselesaikan dalam masa polinomial adalah lebih baik jika hubungannya adalah linear . , dan kualiti tidak sepatutnya menurun apabila n meningkat.
Kajian menyimpulkan: Pada masa ini, pengoptimum berasaskan rangkaian saraf (seperti yang dicadangkan oleh Martin JA Schuetz et al.) tidak memenuhi keperluan di atas dan tidak boleh bersaing dengan algoritma standard mudah untuk menyelesaikan masalah pengoptimuman yang sukar. Adalah penting untuk meneroka sama ada rangkaian saraf boleh memenuhi keperluan ini, atau sama ada terdapat sebab yang lebih mendalam untuk kegagalannya.
Atas ialah kandungan terperinci Rangkaian saraf graf telah diterbitkan dalam sub-jurnal Alam, tetapi ia telah didedahkan bahawa ia adalah 104 kali lebih perlahan daripada algoritma biasa Penanya: Adakah ia ketinggian baru?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Ramalan Harga Worldcoin (WLD) 2025-2031: Adakah WLD akan mencapai $ 4 menjelang 2031?
Apr 21, 2025 pm 02:42 PM
Ramalan Harga Worldcoin (WLD) 2025-2031: Adakah WLD akan mencapai $ 4 menjelang 2031?
Apr 21, 2025 pm 02:42 PM
Worldcoin (WLD) menonjol dalam pasaran cryptocurrency dengan mekanisme pengesahan biometrik dan perlindungan privasi yang unik, menarik perhatian banyak pelabur. WLD telah melakukan yang luar biasa di kalangan altcoin dengan teknologi inovatifnya, terutamanya dalam kombinasi dengan teknologi kecerdasan buatan terbuka. Tetapi bagaimanakah aset digital akan berkelakuan dalam beberapa tahun akan datang? Mari kita meramalkan harga masa depan WLD bersama -sama. Ramalan harga WLD 2025 dijangka mencapai pertumbuhan yang signifikan di WLD pada tahun 2025. Analisis pasaran menunjukkan bahawa harga WLD purata boleh mencapai $ 1.31, dengan maksimum $ 1.36. Walau bagaimanapun, dalam pasaran beruang, harga mungkin jatuh ke sekitar $ 0.55. Harapan pertumbuhan ini disebabkan terutamanya oleh WorldCoin2.
 Kedudukan pertukaran leverage dalam lingkaran mata wang Cadangan terkini sepuluh pertukaran leverage dalam lingkaran mata wang
Apr 21, 2025 pm 11:24 PM
Kedudukan pertukaran leverage dalam lingkaran mata wang Cadangan terkini sepuluh pertukaran leverage dalam lingkaran mata wang
Apr 21, 2025 pm 11:24 PM
Platform yang mempunyai prestasi cemerlang dalam perdagangan, keselamatan dan pengalaman pengguna yang dimanfaatkan pada tahun 2025 adalah: 1. Okx, sesuai untuk peniaga frekuensi tinggi, menyediakan sehingga 100 kali leverage; 2. Binance, sesuai untuk peniaga berbilang mata wang di seluruh dunia, memberikan 125 kali leverage tinggi; 3. Gate.io, sesuai untuk pemain derivatif profesional, menyediakan 100 kali leverage; 4. Bitget, sesuai untuk orang baru dan peniaga sosial, menyediakan sehingga 100 kali leverage; 5. Kraken, sesuai untuk pelabur mantap, menyediakan 5 kali leverage; 6. Bybit, sesuai untuk penjelajah altcoin, menyediakan 20 kali leverage; 7. Kucoin, sesuai untuk peniaga kos rendah, menyediakan 10 kali leverage; 8. Bitfinex, sesuai untuk bermain senior
 Apakah yang dimaksudkan dengan transaksi rantaian rantaian? Apakah urus niaga salib?
Apr 21, 2025 pm 11:39 PM
Apakah yang dimaksudkan dengan transaksi rantaian rantaian? Apakah urus niaga salib?
Apr 21, 2025 pm 11:39 PM
Pertukaran yang menyokong urus niaga rantaian: 1. Binance, 2. Uniswap, 3 Sushiswap, 4. Kewangan Curve, 5. Thorchain, 6. 1 inci Pertukaran, 7.
 Platform Perdagangan Web3 Ranking_Web3 Global Exchanges Top Ten Ringkasan
Apr 21, 2025 am 10:45 AM
Platform Perdagangan Web3 Ranking_Web3 Global Exchanges Top Ten Ringkasan
Apr 21, 2025 am 10:45 AM
Binance adalah tuan rumah ekosistem perdagangan aset digital global, dan ciri -cirinya termasuk: 1. Jumlah dagangan harian purata melebihi $ 150 bilion, menyokong 500 pasangan perdagangan, yang meliputi 98% mata wang arus perdana; 2. Matriks inovasi meliputi pasaran Derivatif, susun atur Web3 dan sistem pendidikan; 3. Kelebihan teknikal adalah enjin yang sepadan dengan milisaat, dengan jumlah pemprosesan puncak sebanyak 1.4 juta transaksi sesaat; 4. Kemajuan pematuhan memegang lesen 15 negara dan menetapkan entiti yang mematuhi di Eropah dan Amerika Syarikat.
 Cara Memenangi Ganjaran Airdrop Kernel pada Strategi Proses Penuh Binance
Apr 21, 2025 pm 01:03 PM
Cara Memenangi Ganjaran Airdrop Kernel pada Strategi Proses Penuh Binance
Apr 21, 2025 pm 01:03 PM
Dalam dunia kriptografi yang ramai, peluang baru selalu muncul. Pada masa ini, aktiviti udara Kerneldao (kernel) menarik banyak perhatian dan menarik perhatian banyak pelabur. Jadi, apakah asalnya projek ini? Apakah faedah yang boleh diperoleh oleh pemegang BNB? Jangan risau, perkara berikut akan mendedahkannya satu demi satu untuk anda.
 'Black Monday Sell' adalah hari yang sukar untuk industri cryptocurrency
Apr 21, 2025 pm 02:48 PM
'Black Monday Sell' adalah hari yang sukar untuk industri cryptocurrency
Apr 21, 2025 pm 02:48 PM
Jatuh di pasaran cryptocurrency telah menyebabkan panik di kalangan pelabur, dan Dogecoin (Doge) telah menjadi salah satu kawasan terkena paling sukar. Harganya jatuh dengan ketara, dan jumlah nilai kunci kewangan yang terdesentralisasi (DEFI) (TVL) juga menyaksikan penurunan yang ketara. Gelombang jualan "Black Monday" menyapu pasaran cryptocurrency, dan Dogecoin adalah yang pertama dipukul. Defitvlnya jatuh ke tahap 2023, dan harga mata wang jatuh 23.78% pada bulan lalu. Defitvl Dogecoin jatuh ke tahap rendah $ 2.72 juta, terutamanya disebabkan oleh penurunan 26.37% dalam indeks nilai SOSO. Platform defi utama lain, seperti DAO dan Thorchain yang membosankan, TVL juga menurun sebanyak 24.04% dan 20.
 Mengapa kenaikan atau kejatuhan harga mata wang maya? Mengapa kenaikan atau kejatuhan harga mata wang maya?
Apr 21, 2025 am 08:57 AM
Mengapa kenaikan atau kejatuhan harga mata wang maya? Mengapa kenaikan atau kejatuhan harga mata wang maya?
Apr 21, 2025 am 08:57 AM
Faktor kenaikan harga mata wang maya termasuk: 1. Peningkatan permintaan pasaran, 2. Menurunkan bekalan, 3. Berita positif yang dirangsang, 4. Sentimen pasaran optimis, 5. Persekitaran makroekonomi; Faktor penurunan termasuk: 1. Mengurangkan permintaan pasaran, 2. Peningkatan bekalan, 3.
 Aavenomics adalah cadangan untuk mengubah suai token protokol AAVE dan memperkenalkan pembelian semula token, yang telah mencapai bilangan kuorum orang.
Apr 21, 2025 pm 06:24 PM
Aavenomics adalah cadangan untuk mengubah suai token protokol AAVE dan memperkenalkan pembelian semula token, yang telah mencapai bilangan kuorum orang.
Apr 21, 2025 pm 06:24 PM
Aavenomics adalah cadangan untuk mengubah token protokol AAVE dan memperkenalkan repos token, yang telah melaksanakan kuorum untuk Aavedao. Marc Zeller, pengasas Rantaian Projek AAVE (ACI), mengumumkan ini pada X, dengan menyatakan bahawa ia menandakan era baru untuk perjanjian itu. Marc Zeller, pengasas Inisiatif Rantaian AAVE (ACI), mengumumkan pada X bahawa cadangan aavenomik termasuk mengubah token protokol AAVE dan memperkenalkan repos token, telah mencapai kuorum untuk Aavedao. Menurut Zeller, ini menandakan era baru untuk perjanjian itu. Ahli -ahli Aavedao mengundi untuk menyokong cadangan itu, yang 100 seminggu pada hari Rabu





