 Peranti teknologi
Peranti teknologi
 AI
AI
 Model penyebaran meletup, ini adalah ulasan dan ringkasan pertama kertas Github
Model penyebaran meletup, ini adalah ulasan dan ringkasan pertama kertas Github
Model penyebaran meletup, ini adalah ulasan dan ringkasan pertama kertas Github
Ulasan ini (Model Penyebaran: Tinjauan Komprehensif Kaedah dan Aplikasi) datang daripada Ming-Hsuan Yang dari University of California & Penyelidikan Google, Cui Bin Laboratory of Peking University, CMU, UCLA, Montreal Mila Research Institute , dsb. Pasukan ini menjalankan ringkasan dan analisis komprehensif model resapan sedia ada buat kali pertama, bermula daripada klasifikasi terperinci algoritma model resapan, kaitannya dengan lima model generatif utama yang lain, dan aplikasinya dalam tujuh bidang utama, dan akhirnya dicadangkan Batasan sedia ada dan arah pembangunan masa depan model resapan dijelaskan.

Pautan artikel: https://arxiv.org/abs/2209.00796 Pautan github ringkasan klasifikasi kertas: https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy
Pengenalan
Model resapan ialah penjanaan mendalam SOTA baharu dalam model . Model resapan mengatasi SOTA asal: GAN dalam tugas penjanaan imej, dan mempunyai prestasi cemerlang dalam banyak bidang aplikasi, seperti penglihatan komputer, NLP, pemprosesan isyarat bentuk gelombang, pemodelan pelbagai mod, pemodelan graf molekul dan pemodelan siri masa , antagonis penyucian, dsb. Selain itu, model resapan berkait rapat dengan bidang penyelidikan lain, seperti pembelajaran teguh, pembelajaran perwakilan, dan pembelajaran pengukuhan. Walau bagaimanapun, model resapan asal juga mempunyai kekurangan Kelajuan pensampelannya adalah perlahan, biasanya memerlukan beribu-ribu langkah penilaian untuk membuat anggaran kebarangkalian maksimumnya tidak setanding dengan model berasaskan kemungkinan kurang berkemampuan. Pada masa kini, banyak kajian telah melakukan banyak usaha untuk menyelesaikan batasan di atas dari perspektif aplikasi praktikal, atau menganalisis keupayaan model dari perspektif teori.
Walau bagaimanapun, terdapat kekurangan semakan sistematik terhadap kemajuan terkini dalam model resapan daripada algoritma kepada aplikasi. Untuk mencerminkan kemajuan dalam bidang yang berkembang pesat ini, kami membentangkan tinjauan komprehensif pertama model penyebaran. Kami membayangkan bahawa kerja kami akan memberi penerangan tentang pertimbangan reka bentuk dan kaedah lanjutan model penyebaran, menunjukkan aplikasinya dalam bidang yang berbeza, dan menunjukkan arah penyelidikan masa depan. Ringkasan ulasan ini ditunjukkan dalam rajah di bawah:
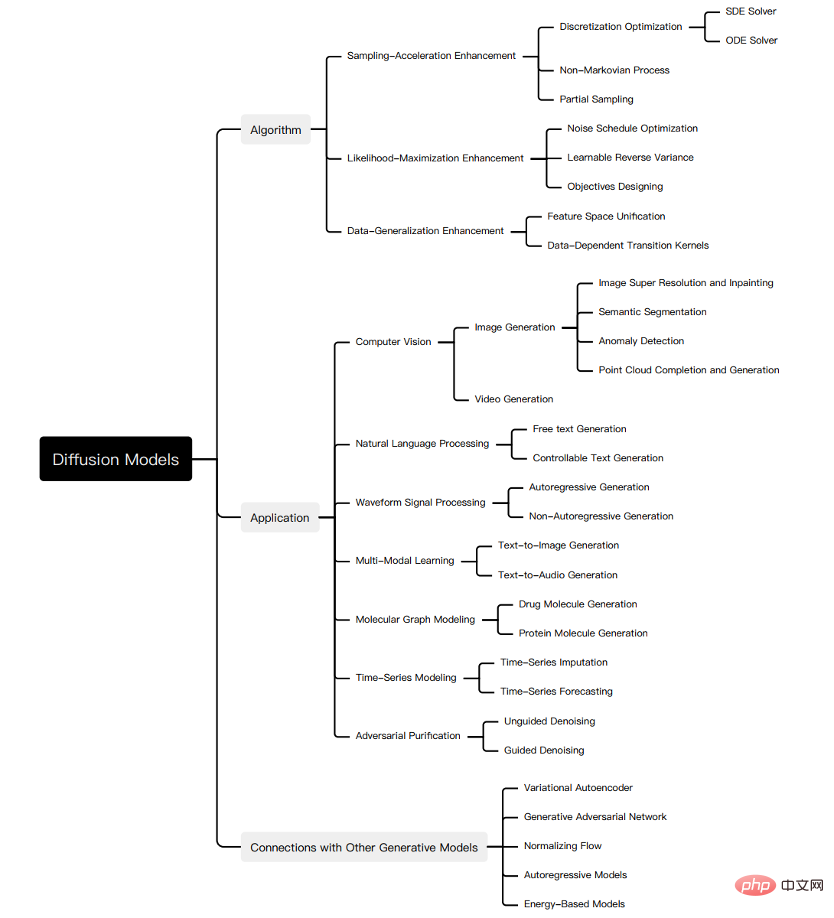
Walaupun model penyebaran mempunyai prestasi hebat dalam pelbagai tugas Ia mempunyai prestasi cemerlang dalam kedua-dua model, tetapi ia masih mempunyai kelemahannya sendiri, dan banyak kajian telah menambah baik model resapan. Untuk menjelaskan secara sistematik kemajuan penyelidikan model resapan, kami meringkaskan tiga kelemahan utama model resapan asal, kelajuan pensampelan yang perlahan, kemungkinan pemaksimuman yang lemah, dan keupayaan generalisasi data yang lemah, dan dicadangkan untuk membahagikan penyelidikan penambahbaikan pada model resapan kepada yang sepadan. Tiga kategori: peningkatan kelajuan pensampelan, peningkatan kemungkinan maksimum dan peningkatan generalisasi data. Kami mula-mula menerangkan motivasi untuk penambahbaikan, dan kemudian mengklasifikasikan penyelidikan dalam setiap arah penambahbaikan mengikut ciri-ciri kaedah, supaya jelas menunjukkan hubungan dan perbezaan antara kaedah. Di sini kami hanya memilih beberapa kaedah penting sebagai contoh Setiap jenis kaedah diperkenalkan secara terperinci dalam kerja kami, seperti yang ditunjukkan dalam rajah:
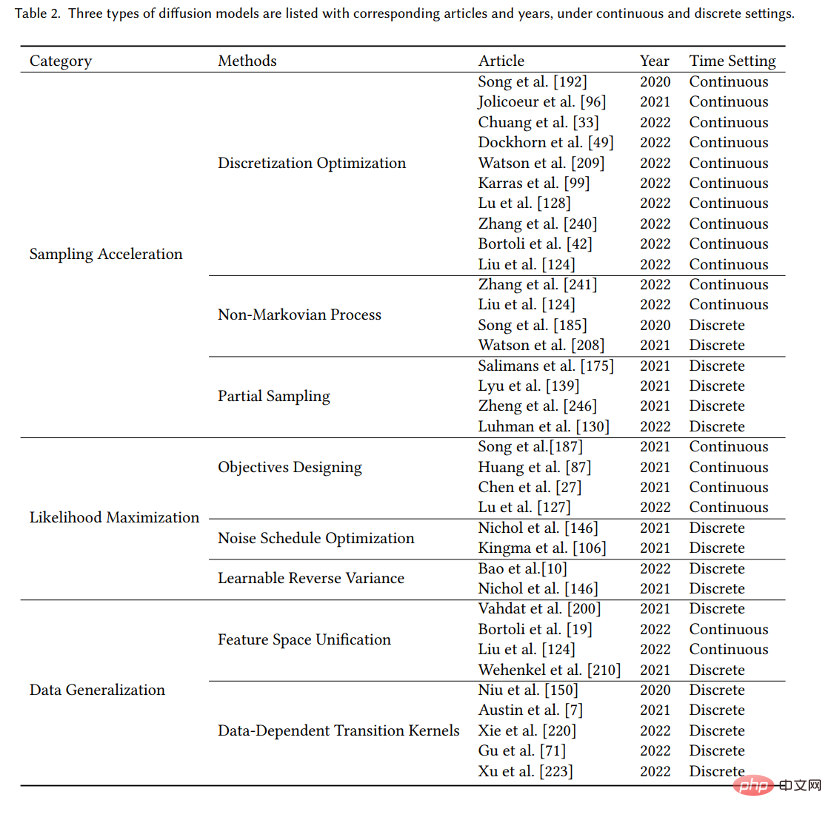
Selepas. menganalisis tiga jenis model resapan, kami akan memperkenalkan lima lagi model generatif GAN, VAE, model Autoregressive, Aliran Normalisasi dan model berasaskan Tenaga. Memandangkan sifat cemerlang model resapan, penyelidik telah menggabungkan model resapan dengan model generatif lain mengikut ciri-cirinya Oleh itu, untuk menunjukkan lagi ciri dan kerja penambahbaikan model resapan, kami memperkenalkan secara terperinci gabungan resapan. model dan model generatif lain berfungsi dan menggambarkan penambahbaikan berbanding model generatif asal. Model resapan mempunyai prestasi cemerlang dalam banyak bidang, dan memandangkan model resapan mempunyai ubah bentuk yang berbeza dalam aplikasi dalam bidang yang berbeza, kami secara sistematik memperkenalkan penyelidikan aplikasi model resapan, termasuk bidang berikut: penglihatan komputer, NLP, Pemprosesan isyarat bentuk gelombang, pemodelan multimodal, pemodelan graf molekul, pemodelan siri masa, penulenan musuh.
Untuk setiap tugasan, kami mentakrifkan tugasan dan memperkenalkan kerja menggunakan model resapan untuk mengendalikan tugasan, Kami meringkaskan sumbangan utama kerja ini seperti berikut:
- Kaedah pengelasan baharu: Kami mencadangkan kaedah pengelasan sistematik baharu untuk model resapan dan aplikasinya . Secara khusus, kami membahagikan model kepada tiga kategori: peningkatan kelajuan pensampelan, peningkatan anggaran kemungkinan maksimum dan peningkatan generalisasi data. Tambahan pula, kami mengklasifikasikan aplikasi model resapan kepada tujuh kategori: penglihatan komputer, NLP, pemprosesan isyarat bentuk gelombang, pemodelan multimodal, pemodelan graf molekul, pemodelan siri masa dan penulenan lawan.
- Semakan Komprehensif: Kami menyediakan gambaran keseluruhan komprehensif pertama model penyebaran moden dan aplikasinya. Kami membentangkan penambahbaikan utama untuk setiap model resapan, membuat perbandingan yang diperlukan dengan model asal, dan meringkaskan kertas yang sepadan. Bagi setiap jenis aplikasi model resapan, kami membentangkan masalah utama yang ditangani oleh model resapan dan menerangkan cara mereka menyelesaikan masalah ini.
- Arah Penyelidikan Masa Depan: Kami membangkitkan soalan terbuka untuk penyelidikan masa depan dan menilai aplikasi model resapan dalam algoritma Beberapa cadangan disediakan untuk perkembangan masa hadapan dalam aplikasi.
Asas Model Penyebaran
Isu teras dalam pemodelan generatif ialah pertukaran antara fleksibiliti model dan kebolehkiraan. Idea asas model resapan adalah untuk mengganggu pengedaran dalam data secara sistematik melalui proses resapan ke hadapan, dan kemudian memulihkan pengedaran data dengan mempelajari proses resapan terbalik, dengan itu menghasilkan yang sangat fleksibel dan mudah dikira. model generatif.
A.Denoising Diffusion Probabilistic Models (DDPM)
A DDPM terdiri daripada dua komposisi rantai Markov berparameter, dan menggunakan inferens variasi untuk menghasilkan sampel yang konsisten dengan pengagihan data asal selepas masa yang terhad. Fungsi rantaian hadapan adalah untuk mengganggu data Ia secara beransur-ansur menambah hingar Gaussian kepada data mengikut jadual hingar yang telah direka bentuk sehingga pengagihan data cenderung kepada pengagihan sebelumnya, iaitu, pengagihan Gaussian standard. Rantaian ke belakang bermula dari sebelumnya yang diberikan dan menggunakan kernel transformasi Gaussian berparameter, belajar untuk memulihkan pengedaran data asal secara beransur-ansur. Menggunakan  untuk mewakili data asal dan pengedarannya, pengedaran rantai hadapan boleh dinyatakan dengan formula berikut:
untuk mewakili data asal dan pengedarannya, pengedaran rantai hadapan boleh dinyatakan dengan formula berikut:
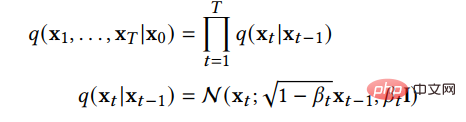
Ini menunjukkan bahawa rantai hadapan ialah proses Markov, x_t ialah sampel selepas menambah t langkah hingar, dan β_t ialah parameter yang mengawal kemajuan hingar yang diberikan terlebih dahulu. Apabila  cenderung kepada 1, x_T boleh kira-kira dianggap mematuhi taburan Gaussian standard. Apabila β_t kecil, isirong pemindahan proses terbalik boleh kira-kira dianggap sebagai Gaussian:
cenderung kepada 1, x_T boleh kira-kira dianggap mematuhi taburan Gaussian standard. Apabila β_t kecil, isirong pemindahan proses terbalik boleh kira-kira dianggap sebagai Gaussian:
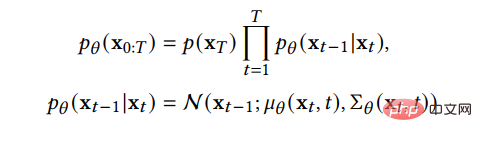
Kita boleh mempelajari sempadan bawah variasi sebagai fungsi kehilangan:
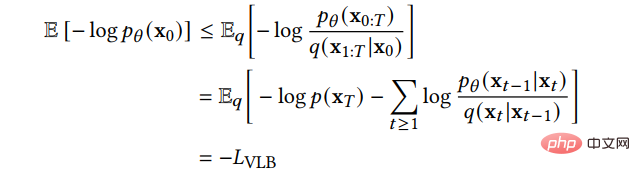
B.Model Generatif Berasaskan Skor (SGM)
Di atas DDPM boleh dianggap sebagai bentuk diskret SGM. SGM membina persamaan pembezaan stokastik (SDE) untuk mengganggu pengedaran data dengan lancar dan mengubah pengedaran data asal kepada pengedaran terdahulu yang diketahui:
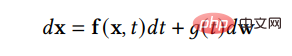
dan SDE songsang sepadan untuk mengubah pengedaran terdahulu kembali kepada pengedaran data asal:
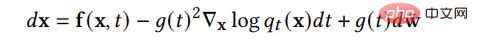
Jadi, untuk membalikkan proses resapan dan menjana data, satu-satunya maklumat yang kami perlukan ialah fungsi pecahan pada setiap titik masa. Menggunakan teknik pemadanan skor, kita boleh mempelajari fungsi skor melalui fungsi kehilangan berikut:
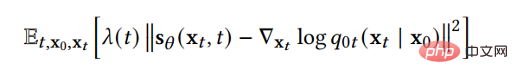
Pengenalan lanjut kepada kedua-dua kaedah dan hubungan antara mereka Lihat artikel kami untuk pengenalan.
Tiga kelemahan utama model resapan asal ialah kelajuan pensampelan yang perlahan, kemungkinan maksimum yang lemah dan keupayaan generalisasi data yang lemah. Banyak kajian terbaru telah menangani kelemahan ini, jadi kami mengklasifikasikan model resapan yang dipertingkatkan kepada tiga kategori: peningkatan kelajuan pensampelan, peningkatan kemungkinan maksimum dan peningkatan generalisasi data. Dalam tiga, empat dan lima bahagian seterusnya kami akan memperkenalkan ketiga-tiga jenis model ini secara terperinci.
Kaedah pecutan pensampelan
Apabila digunakan, untuk mencapai kualiti terbaik bagi sampel baharu, model resapan selalunya memerlukan beribu-ribu langkah pengiraan untuk mendapatkan sampel baharu. sampel. Ini mengehadkan nilai aplikasi praktikal model resapan, kerana dalam aplikasi sebenar, kita selalunya perlu menjana sejumlah besar sampel baharu untuk menyediakan bahan untuk langkah pemprosesan seterusnya. Penyelidik telah menjalankan banyak penyelidikan untuk meningkatkan kelajuan pensampelan model resapan. Kami menerangkan kajian ini secara terperinci. Kami memperhalusinya kepada tiga kaedah: Pengoptimuman Diskretisasi, Proses Bukan Markovian dan Persampelan Separa.
A. Kaedah Pengoptimuman Diskretisasi Kaedah pengoptimuman untuk menyelesaikan SDE penyebaran. Oleh kerana menyelesaikan SDE kompleks dalam realiti hanya boleh menggunakan penyelesaian diskret untuk menganggarkan penyelesaian sebenar, kaedah jenis ini cuba mengoptimumkan kaedah pendiskretan SDE untuk mengurangkan bilangan langkah diskret sambil memastikan kualiti sampel. SGM mencadangkan kaedah umum untuk menyelesaikan proses terbalik, iaitu, kaedah pendiskretan yang sama diguna pakai untuk proses ke hadapan dan ke belakang. Jika SDE hadapan diberi pendiskretan:
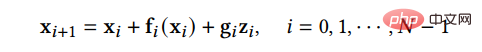
maka kita boleh mendiskrisikan SDE songsang dengan cara yang sama:
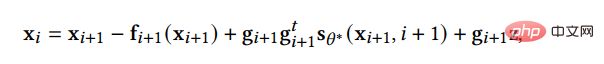
Kaedah ini lebih baik sedikit daripada DDPM mudah. Tambahan pula, SGM menambah pembetul kepada penyelesai SDE supaya sampel yang dihasilkan pada setiap langkah mempunyai pengedaran yang betul. Pada setiap langkah penyelesaian, selepas penyelesai diberi sampel, pelurus menggunakan kaedah Markov rantai Monte Carlo untuk meluruskan pengedaran sampel yang baru dijana. Eksperimen menunjukkan bahawa menambah pembetul kepada penyelesai adalah lebih cekap daripada secara langsung meningkatkan bilangan langkah dalam penyelesai.
B.Proses Bukan Markovian Kaedah ini menembusi batasan Proses Markovian yang asal, dan kaedahnya proses terbalik Setiap langkah boleh bergantung pada lebih banyak sampel lepas untuk meramalkan sampel baharu, jadi ramalan yang lebih baik boleh dibuat walaupun saiz langkahnya besar, sekali gus mempercepatkan proses pensampelan. Kerja utama DDIM tidak lagi menganggap bahawa proses ke hadapan adalah proses Markov, tetapi mematuhi pengedaran berikut:
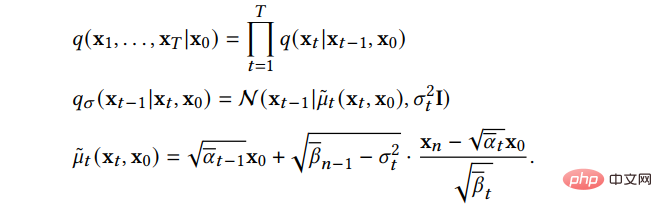
Proses pensampelan DDIM boleh Dirawat sebagai persamaan pembezaan tetap divine discretized, proses pensampelan adalah lebih cekap dan menyokong interpolasi sampel. Kajian lanjut mendapati bahawa DDIM boleh dianggap sebagai kes khas model penyebaran on-manifold PNDM. Kaedah
C.Pensampelan Separa mengabaikan sebahagian daripada nod masa dalam proses penjanaan dan hanya menggunakan bakinya Nod kali seterusnya digunakan untuk menjana sampel, yang secara langsung mengurangkan masa pensampelan. Contohnya, Penyulingan Progresif menyuling model resapan yang lebih cekap daripada model resapan terlatih. Untuk model resapan terlatih, Penyulingan Progresif akan melatih semula model resapan supaya satu langkah model resapan baharu sepadan dengan dua langkah model resapan terlatih, supaya model baharu dapat menjimatkan separuh daripada proses pensampelan model lama. Algoritma khusus adalah seperti berikut:

Mengitar proses penyulingan ini secara berterusan boleh mengurangkan langkah pensampelan secara eksponen.
Peningkatan anggaran kemungkinan maksimum
Prestasi model resapan dalam anggaran kemungkinan maksimum adalah lebih teruk daripada model generatif berdasarkan fungsi kemungkinan, tetapi kebarangkalian maksimum anggaran mempunyai banyak kelebihan Senario aplikasi mempunyai kepentingan yang besar, seperti pemampatan imej, pembelajaran separa penyeliaan dan penulenan musuh. Memandangkan kemungkinan log sukar dikira secara langsung, penyelidikan tertumpu terutamanya pada pengoptimuman dan menganalisis sempadan bawah variasi (VLB). Kami menghuraikan model yang meningkatkan anggaran kemungkinan maksimum model resapan. Kami memperhalusinya kepada tiga kategori kaedah: Reka Bentuk Objektif, Pengoptimuman Jadual Kebisingan dan Varian Songsang Boleh Dipelajari.
A.Merancang Objektif Kaedah ini menggunakan SDE resapan untuk menyimpulkan kebarangkalian log dan fungsi pecahan bagi data yang dihasilkan Memadankan fungsi kehilangan. Dengan cara ini, dengan mereka bentuk fungsi kehilangan yang sesuai, VLB dan kemungkinan log boleh dimaksimumkan. Song et al membuktikan bahawa fungsi berat bagi fungsi kehilangan boleh direka bentuk supaya nilai fungsi kemungkinan sampel yang dihasilkan oleh SDE terbalik plug-in adalah kurang daripada atau sama dengan nilai fungsi kehilangan, iaitu fungsi kehilangan adalah. sempadan atas fungsi kemungkinan. Fungsi kehilangan untuk pemasangan fungsi pecahan adalah seperti berikut:
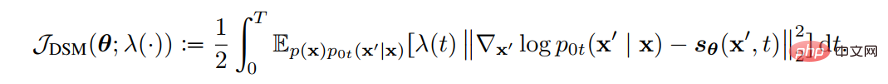
Kita hanya perlu menetapkan fungsi berat λ(t) kepada pekali resapan g( t) Biarkan fungsi kerugian menjadi VLB bagi fungsi kemungkinan, iaitu:
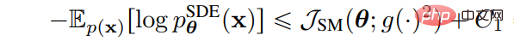
B.Pengoptimuman Jadual Bunyi Meningkatkan VLB dengan mereka bentuk atau mempelajari kemajuan bising proses ke hadapan. VDM membuktikan bahawa apabila langkah diskret menghampiri infiniti, fungsi kehilangan ditentukan sepenuhnya oleh titik akhir fungsi nisbah isyarat-ke-bunyi SNR(t):
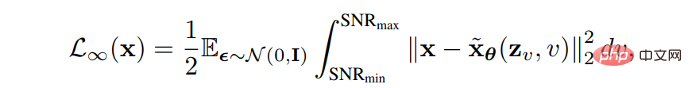
Kemudian dalam Apabila langkah diskret menghampiri infiniti, VLB boleh dioptimumkan dengan mempelajari titik akhir fungsi nisbah isyarat-ke-bunyi SNR(t), dan aspek lain model boleh dipertingkatkan dengan mempelajari nilai fungsi di bahagian tengah fungsi nisbah isyarat-ke-bunyi.
C.Belajar Reverse Variance Kaedah ini mempelajari varians proses songsang, dengan itu mengurangkan ralat pemasangan dan boleh memaksimumkan VLB dengan berkesan. Analitik-DPM membuktikan bahawa terdapat jangkaan dan varians optimum dalam proses songsang dalam DDPM dan DDIM:

Gunakan formula di atas dan terlatih Untuk fungsi pecahan, di bawah syarat-syarat proses ke hadapan yang diberikan, VLB optimum boleh dicapai lebih kurang.
Peningkatan generalisasi data
Model resapan menganggap bahawa data wujud dalam ruang Euclidean, iaitu, manifold dengan geometri satah, dan menambah hingar Gaussian tidak dapat dielakkan. data ke dalam ruang keadaan berterusan, jadi model resapan pada mulanya hanya boleh mengendalikan data berterusan seperti gambar, dan kesan penggunaan terus data diskret atau jenis data lain adalah lemah. Ini mengehadkan senario aplikasi model resapan. Beberapa kerja penyelidikan menyamaratakan model resapan kepada jenis data lain, dan kami menggambarkan kaedah ini secara terperinci. Kami mengklasifikasikannya kepada dua jenis kaedah: Penyatuan Ruang Ciri dan Inti Peralihan Bergantung kepada Data. Kaedah
A.Penyatuan Ruang Ciri menukar data kepada bentuk ruang terpendam bersatu, dan kemudian ruang terpendam tersebar pada. LSGM mencadangkan untuk menukar data kepada ruang terpendam berterusan melalui rangka kerja VAE dan kemudian meresapkannya padanya. Kesukaran kaedah ini ialah bagaimana melatih VAE dan model resapan pada masa yang sama. LSGM menunjukkan bahawa memandangkan pendasar pendasar sukar dikawal, kerugian padanan pecahan tidak lagi terpakai. LSGM secara langsung menggunakan fungsi kehilangan tradisional ELBO dalam VAE sebagai fungsi kehilangan, dan memperoleh hubungan antara ELBO dan padanan skor:
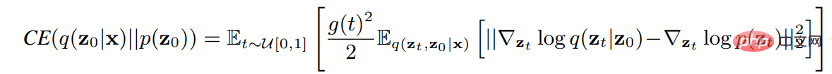
Formula ini berlaku jika pemalar diabaikan. Dengan meparameterkan fungsi pecahan sampel dalam proses resapan, LSGM boleh mempelajari dan mengoptimumkan ELBO dengan cekap.
B.Data-Dependant Transition Kernels Kaedah mereka bentuk inti peralihan dalam proses resapan mengikut ciri jenis data , membenarkan model resapan digunakan secara langsung pada jenis data tertentu. D3PM telah mereka bentuk kernel peralihan untuk data diskret, yang boleh ditetapkan kepada keadaan berjalan rawak malas, menyerap, dsb. GEODIFF mereka bentuk rangkaian neural graf invarian pusingan terjemahan untuk data graf molekul 3D, dan membuktikan bahawa taburan awal invarian dan inti peralihan boleh memperoleh taburan marginal invarian. Katakan T ialah penjelmaan putaran terjemahan, seperti:
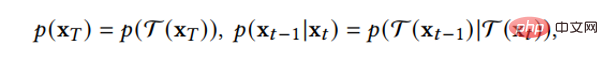
Kemudian taburan sampel yang dijana juga mempunyai invarian putaran terjemahan:
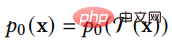
Hubungan dengan model generatif lain Dalam setiap subseksyen di bawah, kami mula-mula memperkenalkan lima jenis model generatif penting yang lain dan menganalisis Kelebihan dan Hadnya. Kami kemudiannya memperkenalkan cara model resapan berkaitan dengannya dan menggambarkan cara model generatif ini boleh dipertingkatkan dengan menggabungkan model resapan. Hubungan antara VAE, GAN, model Autoregresif, Aliran normalisasi, Model berasaskan tenaga dan model resapan ditunjukkan dalam rajah di bawah:
- DDPM boleh dianggap sebagai VAE Markovian hierarki. Tetapi terdapat juga perbezaan antara DDPM dan VAE am. Sebagai VAE, pengekod dan penyahkod DDPM mematuhi pengedaran Gaussian dan mempunyai baris Markov adalah sama dengan dimensi data semua lapisan penyahkod berkongsi rangkaian saraf;
- DDPM boleh membantu GAN menyelesaikan masalah latihan yang tidak stabil. Oleh kerana data berada dalam manifold berdimensi rendah dalam ruang berdimensi tinggi, pengedaran data yang dijana oleh GAN mempunyai pertindihan yang rendah dengan pengedaran data sebenar, mengakibatkan latihan yang tidak stabil. Model resapan menyediakan proses menambah hingar secara sistematik. Ia menambahkan hingar pada data yang dijana dan data sebenar melalui model resapan, dan kemudian menghantar data tambah hingar kepada diskriminator dengan berkesan dan latihan menjadi tidak stabil.
- Alir menormalkan menukar data kepada pengedaran terdahulu melalui fungsi bijection Pendekatan ini mengehadkan keupayaan ekspresi aliran Normalizing, mengakibatkan hasil aplikasi yang lemah. Model resapan analogi menambah hingar pada pengekod, yang boleh meningkatkan keupayaan ekspresi aliran Normalizing Dari perspektif lain, pendekatan ini adalah untuk melanjutkan model resapan kepada model yang juga boleh dipelajari dalam proses ke hadapan.
- Model autoregresif perlu memastikan bahawa data mempunyai struktur tertentu, yang menjadikannya sangat sukar untuk mereka bentuk dan parameter model autoregresif. Latihan model penyebaran memberi inspirasi kepada latihan model autoregresif, yang mengelakkan kesukaran reka bentuk melalui kaedah latihan khusus.
- Model berasaskan tenaga secara langsung memodelkan pengedaran data asal, tetapi pemodelan langsung menyukarkan pembelajaran dan pensampelan. Dengan menggunakan kemungkinan pemulihan resapan, model mula-mula boleh menambah sedikit hingar pada sampel, dan kemudian membuat kesimpulan taburan sampel asal daripada taburan sampel yang sedikit bising, menjadikan proses pembelajaran dan pensampelan lebih mudah dan lebih stabil.
Aplikasi Model Resapan
Dalam bahagian ini, kami memperkenalkan aplikasi model resapan dalam penglihatan komputer, pemprosesan bahasa semula jadi, pemprosesan isyarat bentuk gelombang dan pelbagai -mod. Aplikasi dalam tujuh arah aplikasi utama, termasuk pembelajaran dinamik, penjanaan graf molekul, siri masa, dan pembelajaran lawan, dan kaedah dalam setiap jenis aplikasi dibahagikan dan dianalisis. Contohnya, dalam penglihatan komputer, model resapan boleh digunakan untuk penyiapan dan pembaikan imej (RePaint):
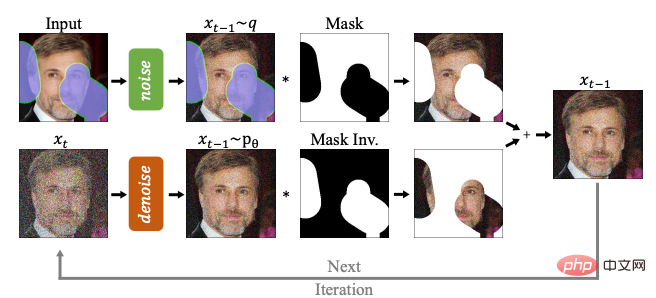
Model resapan boleh digunakan untuk penjanaan teks ke imej (GLIDE) dalam tugasan berbilang modal:

Anda boleh juga Gunakan model resapan untuk menjana molekul dadah dan molekul protein dalam penjanaan graf molekul (GeoDiff):
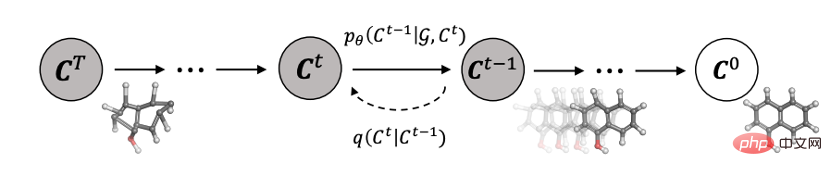
Ringkasan klasifikasi aplikasi ditunjukkan dalam jadual:
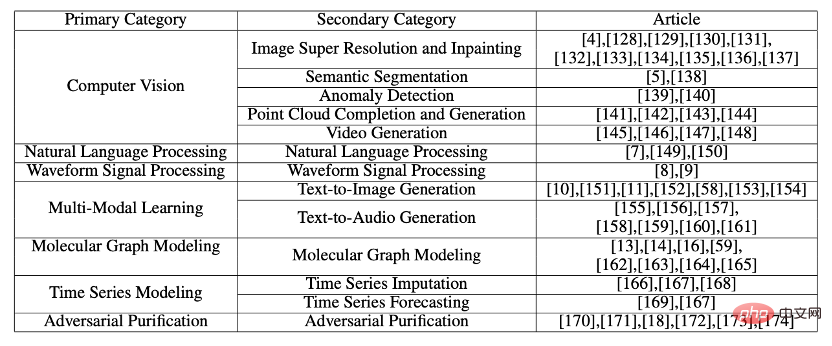
Hala tuju penyelidikan masa hadapan
- Gunakan ujian semula hipotesis. Kami perlu meneliti andaian yang diterima umum yang kami buat dalam permohonan kami. Sebagai contoh, dalam amalan, secara amnya dipercayai bahawa proses ke hadapan model resapan akan mengubah data menjadi taburan Gaussian piawai, tetapi ini tidak berlaku lebih banyak langkah resapan ke hadapan akan menjadikan pengedaran sampel akhir lebih dekat dengan Gaussian standard pengedaran, selaras dengan proses persampelan ; tetapi lebih banyak langkah penyebaran ke hadapan juga membuat anggaran fungsi pecahan lebih sukar. Keadaan teori sukar diperoleh, lantas membawa kepada ketidakpadanan antara teori dan amalan dalam amalan. Kita harus sedar akan situasi ini dan mereka bentuk model resapan yang sesuai.
- Dari masa diskret kepada masa berterusan. Disebabkan oleh fleksibiliti model resapan, banyak kaedah empirikal boleh dipertingkatkan dengan analisis lanjut. Idea penyelidikan ini menjanjikan dengan menukar model masa diskret kepada model masa berterusan yang sepadan dan kemudian mereka bentuk kaedah diskret yang lebih banyak dan lebih baik.
- Proses generasi baharu. Model resapan menjana sampel melalui dua kaedah utama: satu ialah mendiskrisikan SDE resapan songsang, dan kemudian menjana sampel melalui SDE songsang diskret yang satu lagi ialah menggunakan sifat Markov bagi proses songsang untuk mengecilkan sampel secara progresif. Walau bagaimanapun, untuk beberapa tugas, adalah sukar untuk menggunakan kaedah ini untuk menjana sampel dalam amalan. Oleh itu, kajian lanjut terhadap proses dan perspektif generatif baharu diperlukan.
- Generalkan kepada senario yang lebih kompleks dan lebih banyak bidang penyelidikan. Walaupun model resapan telah digunakan pada banyak senario, kebanyakannya terhad kepada senario input tunggal dan output tunggal Pada masa hadapan, anda boleh mempertimbangkan untuk menerapkannya pada senario yang lebih kompleks, seperti sintesis pertuturan teks kepada audiovisual. Anda juga boleh mempertimbangkan untuk menggabungkannya dengan lebih banyak bidang penyelidikan.
Atas ialah kandungan terperinci Model penyebaran meletup, ini adalah ulasan dan ringkasan pertama kertas Github. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Bagaimanakah uvicorn terus mendengar permintaan http tanpa serving_forever ()?
Apr 01, 2025 pm 10:51 PM
Bagaimanakah uvicorn terus mendengar permintaan http tanpa serving_forever ()?
Apr 01, 2025 pm 10:51 PM
Bagaimanakah Uvicorn terus mendengar permintaan HTTP? Uvicorn adalah pelayan web ringan berdasarkan ASGI. Salah satu fungsi terasnya ialah mendengar permintaan HTTP dan teruskan ...
 Bagaimana secara dinamik membuat objek melalui rentetan dan panggil kaedahnya dalam Python?
Apr 01, 2025 pm 11:18 PM
Bagaimana secara dinamik membuat objek melalui rentetan dan panggil kaedahnya dalam Python?
Apr 01, 2025 pm 11:18 PM
Di Python, bagaimana untuk membuat objek secara dinamik melalui rentetan dan panggil kaedahnya? Ini adalah keperluan pengaturcaraan yang biasa, terutamanya jika perlu dikonfigurasikan atau dijalankan ...
 Di era CHATGPT, bagaimanakah masyarakat Q & A teknikal dapat bertindak balas terhadap cabaran?
Apr 01, 2025 pm 11:51 PM
Di era CHATGPT, bagaimanakah masyarakat Q & A teknikal dapat bertindak balas terhadap cabaran?
Apr 01, 2025 pm 11:51 PM
Komuniti Q & A Teknikal di Era CHATGPT: Strategi Respons Segmentfault StackOverflow ...
 Bagaimana untuk mengendalikan ralat 'Pipa Tertutup' dengan baik dalam komunikasi paip pelbagai proses Python?
Apr 01, 2025 pm 11:12 PM
Bagaimana untuk mengendalikan ralat 'Pipa Tertutup' dengan baik dalam komunikasi paip pelbagai proses Python?
Apr 01, 2025 pm 11:12 PM
Python Multi-Process Pipa Ralat "Paip ditutup"? Semasa menggunakan kaedah paip dalam modul multiprocessing Python untuk komunikasi proses ibu bapa dan kanak-kanak, anda mungkin menghadapi ...
 Bagaimana untuk menyelesaikan masalah kandungan pemuatan dinamik yang hilang apabila mendapatkan data laman web?
Apr 01, 2025 pm 11:24 PM
Bagaimana untuk menyelesaikan masalah kandungan pemuatan dinamik yang hilang apabila mendapatkan data laman web?
Apr 01, 2025 pm 11:24 PM
Masalah dan penyelesaian yang dihadapi apabila menggunakan Perpustakaan Permintaan untuk merangkak data laman web. Apabila menggunakan Perpustakaan Permintaan untuk mendapatkan data laman web, anda kadang -kadang menemui ...
 Bagaimana untuk menggunakan Go atau Rust untuk memanggil skrip Python untuk mencapai pelaksanaan selari yang benar?
Apr 01, 2025 pm 11:39 PM
Bagaimana untuk menggunakan Go atau Rust untuk memanggil skrip Python untuk mencapai pelaksanaan selari yang benar?
Apr 01, 2025 pm 11:39 PM
Bagaimana untuk menggunakan Go atau Rust untuk memanggil skrip Python untuk mencapai pelaksanaan selari yang benar? Baru -baru ini saya telah menggunakan python ...
 Cara Mengendalikan Penalaan Prestasi Zookeeper di Debian
Apr 02, 2025 am 07:42 AM
Cara Mengendalikan Penalaan Prestasi Zookeeper di Debian
Apr 02, 2025 am 07:42 AM
Artikel ini menerangkan cara mengoptimumkan prestasi zookeeper pada sistem Debian. Kami akan memberi nasihat mengenai perkakasan, sistem operasi, konfigurasi dan pemantauan zookeeper. 1. Mengoptimumkan peningkatan media penyimpanan di peringkat sistem: Menggantikan pemacu keras mekanikal tradisional dengan pemacu keadaan pepejal SSD akan meningkatkan prestasi I/O dengan ketara dan mengurangkan latensi akses. Lumpuhkan partition swap: Dengan menyesuaikan parameter kernel, mengurangkan pergantungan pada partition swap dan elakkan kerugian prestasi yang disebabkan oleh memori yang kerap dan swap cakera. Meningkatkan Had Upper Descriptor Fail: Meningkatkan bilangan deskriptor fail yang dibenarkan dibuka pada masa yang sama oleh sistem untuk mengelakkan batasan sumber yang mempengaruhi kecekapan pemprosesan Zookeeper. 2. Zookeeper Configuration Optimization Zoo.cfg Konfigurasi Fail
 Cara Melakukan Tetapan Keselamatan Oracle di Debian
Apr 02, 2025 am 07:48 AM
Cara Melakukan Tetapan Keselamatan Oracle di Debian
Apr 02, 2025 am 07:48 AM
Untuk mengukuhkan keselamatan pangkalan data Oracle pada sistem Debian, ia memerlukan banyak aspek untuk bermula. Langkah -langkah berikut menyediakan rangka kerja untuk konfigurasi yang selamat: 1. Pemasangan pangkalan data Oracle dan Penyediaan Sistem Konfigurasi Awal: Pastikan sistem Debian telah dikemas kini ke versi terkini, konfigurasi rangkaian adalah betul, dan semua pakej perisian yang diperlukan dipasang. Adalah disyorkan untuk merujuk kepada dokumen rasmi atau sumber pihak ketiga yang boleh dipercayai untuk pemasangan. Pengguna dan Kumpulan: Buat Kumpulan Pengguna Oracle yang berdedikasi (seperti Oinstall, DBA, BackupDBA) dan menetapkan kebenaran yang sesuai untuknya. 2. Sekatan keselamatan menetapkan sekatan sumber: edit /etc/security/limits.d/30-oracle.conf





