 Peranti teknologi
Peranti teknologi
 AI
AI
 Ramalan trajektori dan perancangan untuk pemanduan autonomi di bawah penggabungan paksa
Ramalan trajektori dan perancangan untuk pemanduan autonomi di bawah penggabungan paksa
Ramalan trajektori dan perancangan untuk pemanduan autonomi di bawah penggabungan paksa
Secara umumnya, penggabungan merupakan tugas yang mencabar untuk pemanduan autonomi dan pemanduan, terutamanya dalam senario aliran trafik yang padat, kerana kenderaan penggabungan biasanya perlu berinteraksi dengan kenderaan lain untuk mengenal pasti Atau mewujudkan ruang untuk penggabungan yang selamat. Kertas kerja ini mengkaji masalah kawalan kenderaan autonomi dalam senario penggabungan paksa. Kami mencadangkan pengawal berasaskan permainan baharu yang dipanggil pengawal permainan pengikut pemimpin (LFGC).
Antaranya, model permainan ketua-pengikut yang agak besar digunakan untuk memodelkan interaksi antara kenderaan autonomi dan kenderaan lain dengan niat pemanduan yang tidak pasti. LFGC menganggarkan niat kenderaan lain dalam talian berdasarkan trajektori yang diperhatikan, meramalkan trajektori masa depan mereka dan menggunakan kawalan ramalan model (MPC) untuk merancang trajektori kenderaan sendiri bagi memastikan kebarangkalian keselamatan semasa mencapai matlamat gabungan. Untuk mengesahkan prestasi LFGC, kami mengujinya menggunakan simulasi dan data NGSIM, di mana LFGC menunjukkan kadar kejayaan penggabungan sehingga 97.5%.
01 Pengenalan
Realisasi kenderaan berautonomi tinggi masih menghadapi banyak cabaran [4]. penting Ia adalah senario yang mencabar untuk pemanduan berawak dan autonomi. Penggabungan paksa biasanya merujuk kepada senario di mana lorong semasa berakhir dan penggabungan paksa diperlukan, seperti penggabungan di tanjakan pintu masuk lebuh raya. Dalam trafik sesak, kenderaan yang bergabung berinteraksi dan/atau bekerjasama dengan kenderaan yang bergerak di lorong sasaran.
Pada masa ini, kenderaan di lorong sasaran boleh memilih untuk mengabaikan kenderaan yang bergabung (iaitu, terus memandu pada masa ini, kenderaan yang bergabung hanya boleh bergabung di belakangnya; atau, di lorong sasaran Kenderaan boleh memilih untuk menyerah kepada cantuman (iaitu, benarkan kenderaan yang bergabung bergabung di hadapannya). Untuk berjaya bergabung ke dalam aliran trafik yang padat, pengawal kenderaan autonomi perlu meramalkan dengan munasabah niat kenderaan di lorong sasaran untuk meneruskan atau mengalah untuk bertindak balas dengan sewajarnya.
Pada masa yang sama, niat kereta lain bergantung bukan sahaja pada keadaan lalu lintas (seperti kedudukan relatif dan kelajuan antara kedua-dua kereta), tetapi juga pada pemanduan am pemandu gaya dan personaliti, emosi, dsb. Sebagai contoh, pemandu yang agresif mungkin cenderung untuk terus memandu, manakala pemandu yang berhati-hati dan konservatif mungkin cenderung untuk mengalah. Ini menimbulkan cabaran besar kepada perancangan dan kawalan kenderaan autonomi.
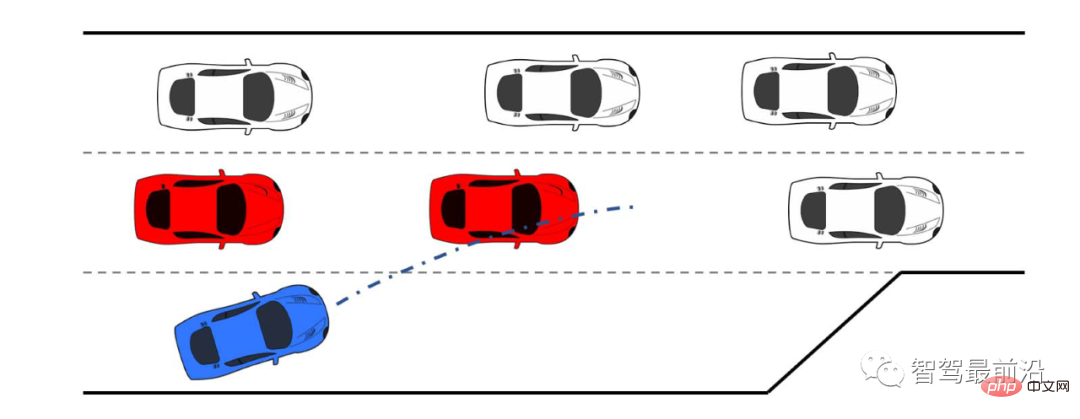
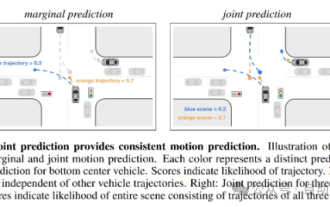
Rajah 1 Adegan gabungan paksa kenderaan sendiri berwarna biru
Ramai cendekiawan pada masa ini menggunakan rangka kerja Proses Keputusan Markov yang Boleh Dicerap Separa (POMDP) untuk menangani ketidakpastian interaksi (contohnya, disebabkan oleh niat kerjasama yang berbeza bagi kereta lain Walau bagaimanapun, kaedah ini mempunyai keperluan pengiraan yang tinggi [). 11], yang sukar digunakan untuk interaksi berbilang kenderaan.
Kaedah pembelajaran tetulang (RL) ialah satu lagi kaedah popular untuk menetapkan strategi kawalan untuk menukar lorong atau senario penggabungan [12][13]. Kaedah berasaskan RL mempunyai keupayaan untuk mengendalikan senario interaksi berbilang kenderaan yang kompleks di bawah trafik, tetapi RL tidak mempunyai kebolehtafsiran dan jaminan keselamatan yang jelas.
Untuk mencapai kawalan yang lebih boleh ditafsir, sesetengah penyelidik telah mencadangkan untuk menambah model ramalan interaksi kenderaan secara eksplisit pada algoritma kawalan. Sebagai contoh, [22] menggunakan "Social Generative Adversarial Network (GAN)" untuk meramalkan trajektori masa depan kereta lain sebagai tindak balas kepada tingkah laku kereta sendiri. Walau bagaimanapun, SocialGAN tidak mengambil kira perubahan dalam gaya dan niat pemandu, dan memerlukan data trafik yang besar [23] untuk latihan beberapa kajian menggunakan kaedah teori permainan untuk memodelkan senario perubahan lorong atau penggabungan [9], [25], Interaksi kenderaan; di bawah [26], [27], [28], [29] boleh mengambil kira gaya pemanduan dan/atau niat yang berbeza, seperti melalui pemodelan permainan dan anggaran dalam talian tahap kognitif pemandu [26] atau [ 30], [31 ].
Dalam kertas kerja ini, algoritma kawalan lanjutan baharu yang dipanggil pengawal permainan pemimpin-pengikut (LFGC) dicadangkan untuk kenderaan autonomi dalam senario penggabungan paksa. Dalam LFGC, teori permainan eksplisit digunakan untuk memodelkan niat interaksi pemandu (teruskan atau hasil) dan tingkah laku kenderaan yang terhasil.
Oleh kerana model mempunyai berbilang pasangan ketua-pengikut selari, ia dipanggil permainan ketua-pengikut [32]. Memandangkan ketidakpastian interaksi, hubungan pemimpin-pengikut yang tidak pasti antara dua kenderaan dimodelkan sebagai pembolehubah terpendam. LFGC menganggarkan hubungan pemimpin-pengikut dalam talian berdasarkan trajektori yang diperhatikan dan menggunakan strategi berasaskan kawalan ramalan model (MPC) untuk membuat keputusan optimum bagi kenderaan autonomi.
Oleh itu, LFGC yang dicadangkan disesuaikan untuk menilai hubungan pemimpin-pengikut yang diramalkan untuk memastikan keselamatan kebarangkalian semasa mencapai penggabungan.
Berbanding dengan kaedah sedia ada, sumbangan dan inovasi LFGC adalah seperti berikut:
1) Gunakan model permainan LFGC untuk ramalan trajektori kenderaan , dengan mengambil kira Niat interaksi dan kerjasama kenderaan lain disambungkan kepada kawalan MPC untuk menjana pelan kawalan yang boleh ditafsir.
2) LFGC mengendalikan interaksi disebabkan oleh niat kerjasama yang berbeza bagi kenderaan lain dengan memodelkan ketidakpastian sebagai pembolehubah terpendam dan anggaran dalam talian inferens Bayesian berdasarkan koleksi trajektori pemerhatian sejarah Ketidakpastian.
3) LFGC menetapkan kekangan terhadap keperluan keselamatan kenderaan (seperti mengelakkan perlanggaran) dan melakukan pengoptimuman sambil memenuhi ciri keselamatan kebarangkalian yang jelas (iaitu dalam sempadan kebarangkalian keselamatan yang ditentukan pengguna) .
4) LFGC direka bentuk di bawah tetapan ruang keadaan berterusan, yang mengurangkan kos pengkomputeran ruang diskret dan boleh mengendalikan senario interaksi berbilang kenderaan yang lebih kompleks.
5) Kebolehlaksanaan LFGC telah disahkan melalui kajian kes berasaskan simulasi yang komprehensif, termasuk kes di mana kenderaan lain dikawal oleh pelbagai jenis model pemandu, dan di NGSIM US Highway 101 Actual kes dalam dataset [34]. Dan dalam simulasi kes sebenar, ia menunjukkan kadar kejayaan sehingga 97.5%.
02 Model dan penerangan strategi kawalan
Dalam bahagian ini, kenderaan sendiri berasaskan MPC diwujudkan berdasarkan model yang mewakili kenderaan dan dinamik trafik.
Model Dinamik Kenderaan
Dalam penggunaan kami model basikal kinematik [35], penerusan basikal model Persamaan masa adalah seperti berikut,
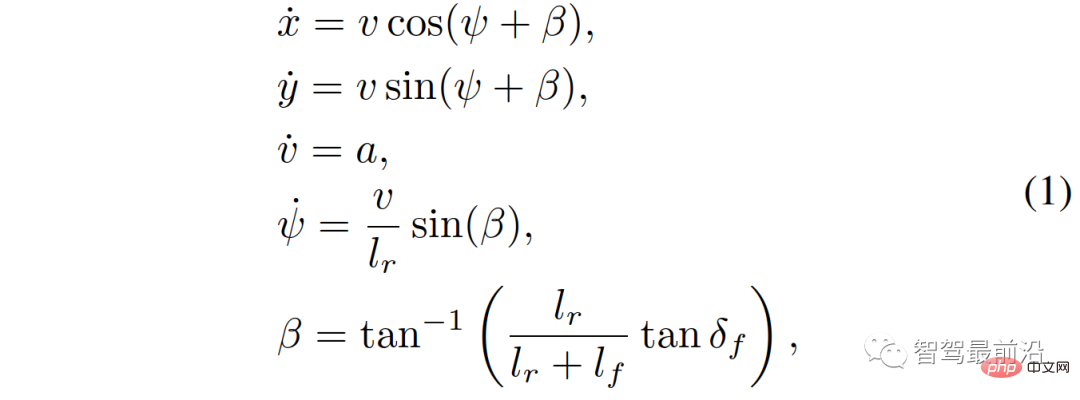
Andaikan hanya stereng roda hadapan  , tiada stereng roda belakang (iaitu
, tiada stereng roda belakang (iaitu  ); x, y ialah kedudukan membujur dan sisi kenderaan; sudut kenderaan;
); x, y ialah kedudukan membujur dan sisi kenderaan; sudut kenderaan;  dan
dan 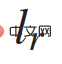 mewakili jarak kenderaan dari CG ke roda hadapan dan gandar belakang a ialah pecutan sepanjang arah kelajuan v. Input kawalan ialah pecutan dan stereng roda hadapan,
mewakili jarak kenderaan dari CG ke roda hadapan dan gandar belakang a ialah pecutan sepanjang arah kelajuan v. Input kawalan ialah pecutan dan stereng roda hadapan, 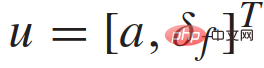 .
.
Tetapan trafik dinamik
Tempat kejadian termasuk 1 kenderaan sendiri dan n kenderaan lain, lalu lintas keadaan dan dinamiknya dicirikan oleh pengagregatan keadaan dan dinamik semua kenderaan n+1. Khususnya, model masa diskret berikut digunakan untuk menerangkan dinamik trafik:
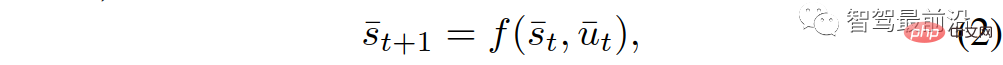
di mana, 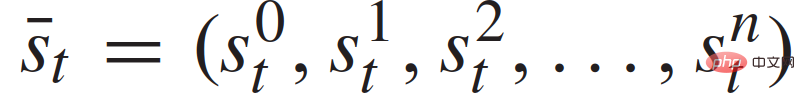
mewakili status trafik kenderaan n+1 pada masa yang berbeza dan 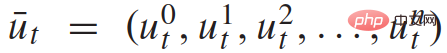 mewakili set input kawalan semua kenderaan n+1 pada masa t. Status setiap kenderaan
mewakili set input kawalan semua kenderaan n+1 pada masa t. Status setiap kenderaan 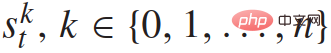 termasuk koordinat xy, kelajuan dan sudut yawnya
termasuk koordinat xy, kelajuan dan sudut yawnya 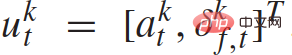
Fungsi ganjaran
Fungsi ganjaran  ialah perwakilan matematik matlamat pemanduan pemandu, dan keadaan trafik terdiri daripada keadaan kedua-dua kenderaan ini , dan ganjaran yang diperolehi oleh kereta sendiri bergantung kepada status dan input kawalan kedua-dua kereta yang berinteraksi. Kami menganggap
ialah perwakilan matematik matlamat pemanduan pemandu, dan keadaan trafik terdiri daripada keadaan kedua-dua kenderaan ini , dan ganjaran yang diperolehi oleh kereta sendiri bergantung kepada status dan input kawalan kedua-dua kereta yang berinteraksi. Kami menganggap 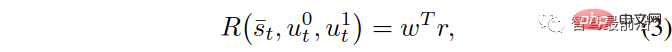 Antaranya,
Antaranya, 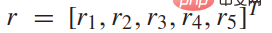 ,
,  ialah vektor berat. Item bonus
ialah vektor berat. Item bonus  mewakili pertimbangan biasa berikut semasa memandu: 1) Keselamatan
mewakili pertimbangan biasa berikut semasa memandu: 1) Keselamatan 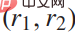 , iaitu tidak berlanggar dengan kereta lain atau meninggalkan jalan raya;
, iaitu tidak berlanggar dengan kereta lain atau meninggalkan jalan raya; 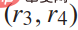 iaitu jarak dari lorong destinasi; 3) Keselesaan
iaitu jarak dari lorong destinasi; 3) Keselesaan 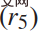 iaitu menjaga jarak yang munasabah dari kereta lain. Untuk takrifan yang lebih terperinci tentang
iaitu menjaga jarak yang munasabah dari kereta lain. Untuk takrifan yang lebih terperinci tentang  , lihat [33].
, lihat [33].
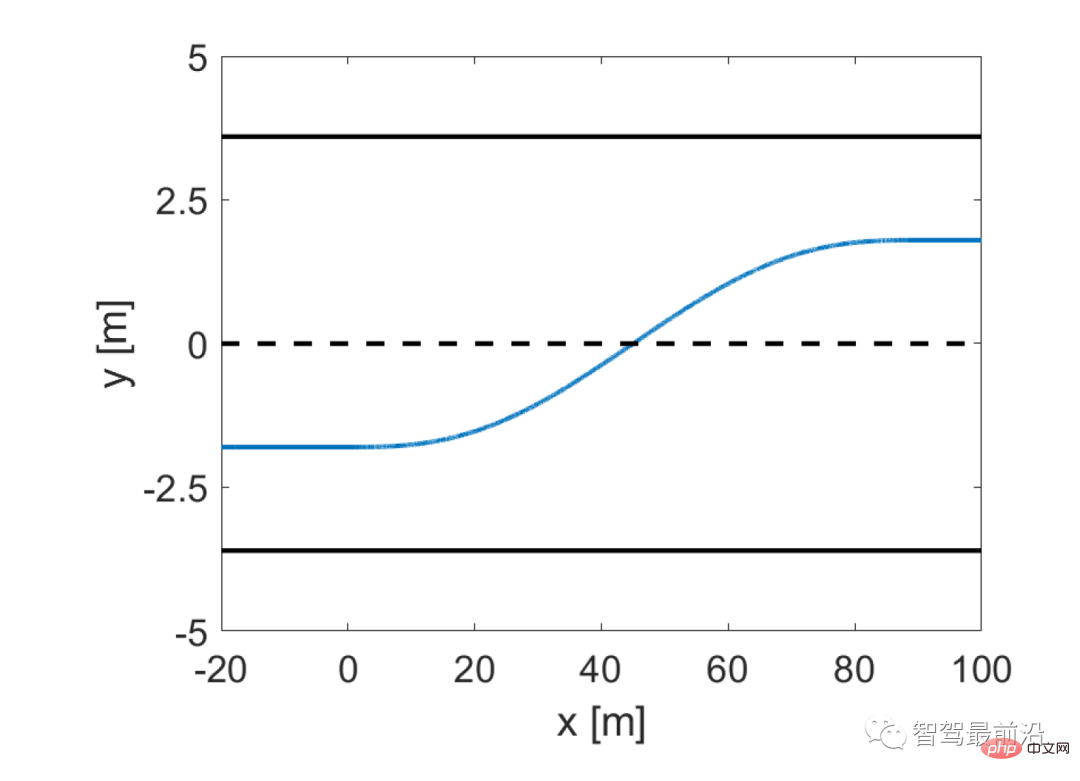
Rajah 2 Lorong menukar lengkung trajektori dengan lima darjah kebebasan
Pilih trajektori sebagai gerakan kenderaan
Kami menganggap sampel trajektori gerakan kenderaan pada 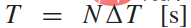 sebagai Tindakan ruang untuk setiap kenderaan. Secara khusus, setiap trajektori ialah sejarah masa keadaan kenderaan
sebagai Tindakan ruang untuk setiap kenderaan. Secara khusus, setiap trajektori ialah sejarah masa keadaan kenderaan 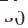
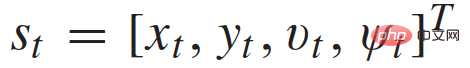 . Menurut model dinamik kenderaan (1), sejarah masa input kawalan yang sepadan dengan setiap trajektori
. Menurut model dinamik kenderaan (1), sejarah masa input kawalan yang sepadan dengan setiap trajektori
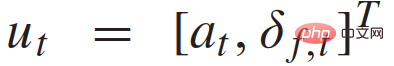 boleh dikira.
boleh dikira.
Untuk kenderaan interaktif yang bergerak di lorong sasaran, kami hanya mempertimbangkan gerakan membujurnya.
Dengan andaian  dan
dan  , model kinematik (1) kenderaan ini dipermudahkan kepada:
, model kinematik (1) kenderaan ini dipermudahkan kepada: 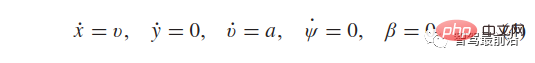
Pada masa ini, trajektori bermula dari keadaan awal yang diberikan hanya bergantung pada pecutan a [0, T]. Pada setiap masa sampel, 81 lengkung pecutan dipertimbangkan, iaitu, 81 trajektori yang memenuhi ungkapan (4), sekali gus membentuk julat trajektori yang boleh dilaksanakan bagi kenderaan lain yang memandu di lorong sasaran.
81 trajektori ini mematuhi kekangan kelajuan 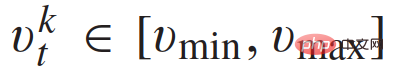 .
.
Nyatakan setiap trajektori sebagai 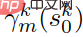 , m = 1,2,...81, dan set trajektori dilambangkan sebagai
, m = 1,2,...81, dan set trajektori dilambangkan sebagai 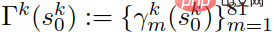
Strategi trajektori kenderaan penggabungan termasuk menjaga lorong dan menukar lorong Penjanaan trajektori mengekalkan lorong adalah serupa dengan (4), dan trajektori menukar lorong diwakili oleh polinomial tertib kelima [37]. Iaitu, penyelesaian kepada keperluan trajektori perubahan lorong boleh dimodelkan sebagai masalah nilai sempadan berikut:
Cari pekali  dan
dan  , supaya polinomial tertib ke-5
, supaya polinomial tertib ke-5
Penuhi syarat nilai awal dan syarat nilai akhir yang sepadan. Pembolehubah ζ dalam (5) mewakili masa berterusan, dan ζ=0 untuk sampel semasa.
Ia juga diandaikan bahawa 1) kenderaan boleh mula menukar lorong pada bila-bila masa sampel dalam julat perancangan, 2) masa yang diperlukan untuk pertukaran lorong lengkap adalah malar [37] . Membenarkan kenderaan untuk menamatkan tingkah laku pertukaran lorongnya pada bila-bila masa semasa proses pertukaran lorong mewakili "perubahan fikiran" pemandu apabila pertukaran lorong yang dirancang sebelum ini menjadi tidak dapat dilaksanakan/selamat. Trajektori selepas membatalkan pertukaran lorong dijana dengan cara yang serupa dengan trajektori pertukaran lorong.
Akhir sekali, trajektori menjaga lorong, menukar lorong dan meninggalkan pertukaran lorong disambung dan digabungkan menjadi 162 trajektori, yang digunakan sebagai kawasan strategi yang boleh dilaksanakan.
Ciri trajektori diekstrak sebagai: 1) sama ada/bila hendak memulakan pertukaran lorong; 2) sama ada/bila untuk menamatkan pertukaran lorong yang tidak sesuai.
Rajah 3 menunjukkan set pensampelan trajektori apabila kenderaan tidak mula menukar lorong dan ketika kenderaan dalam proses menukar lorong. Nyatakan setiap trajektori sebagai,m = 1,2,...,162 set trajektori ialah,.
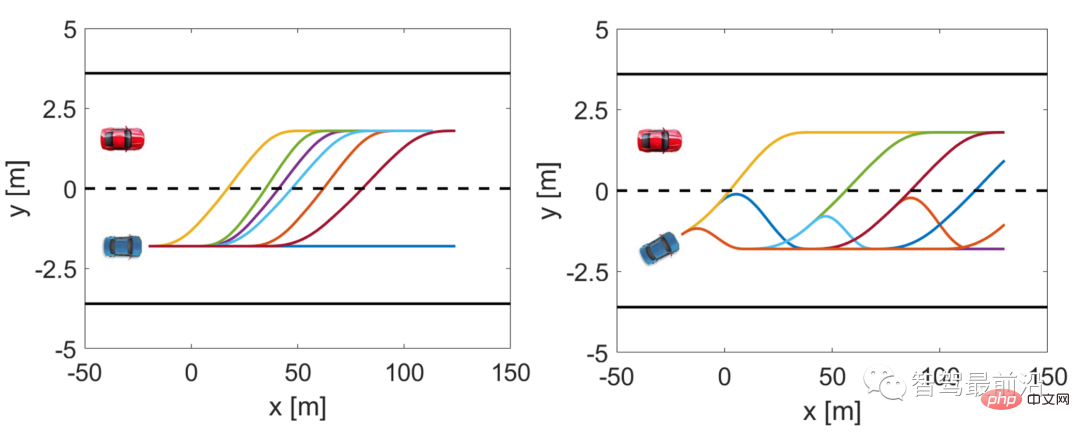
Rajah 3 Sampel trajektori kenderaan yang digabungkan
Ringkasnya definisi Trajektori yang boleh dilaksanakan sebagai output keputusan. Pada masa yang sama, sejarah masa input kawalan yang sepadan dengan trajektori ini boleh dikira berdasarkan model dinamik kenderaan (1). Trajektori yang dirancang sebenarnya boleh dipindahkan ke pengawal gerakan kenderaan asas.
Model Strategi Kawalan Ramalan
Pertimbangkan strategi perancangan trajektori kenderaan autonomi berasaskan MPC, dengan mengambil kira isyarat Kewujudan kenderaan interaktif: Pada setiap masa sampel t, kenderaan sendiri mengira trajektori optimum, 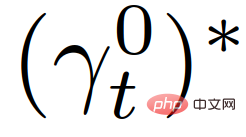 , berdasarkan memaksimumkan ganjaran terkumpulnya dalam julat perancangan:
, berdasarkan memaksimumkan ganjaran terkumpulnya dalam julat perancangan:
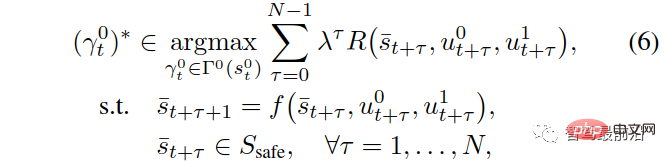
Antaranya, 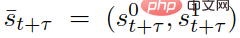 mewakili ramalan status trafik pada masa t+τ diskret, dan
mewakili ramalan status trafik pada masa t+τ diskret, dan 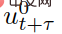 dan
dan 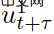
masing-masing mewakili input kawalan yang diramalkan bagi kenderaan sendiri dan kenderaan interaktif di t+τ. Parameter λ∈(0,1) ialah pekali untung dan rugi ganjaran masa hadapan, iaitu keutamaan diberikan kepada ganjaran semasa. Dalam (6), 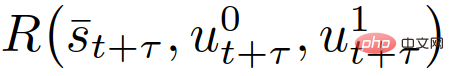
mewakili ganjaran kenderaan sendiri di t+τ, seperti yang diterangkan dalam Bahagian II-C, dan  mewakili satu set nilai keselamatan untuk keadaan lalu lintas, digunakan untuk menguatkuasakan Spesifikasi keselamatan yang ketat (seperti anti-perlanggaran, kekangan sempadan jalan, dsb.). Selepas mendapat trajektori optimum
mewakili satu set nilai keselamatan untuk keadaan lalu lintas, digunakan untuk menguatkuasakan Spesifikasi keselamatan yang ketat (seperti anti-perlanggaran, kekangan sempadan jalan, dsb.). Selepas mendapat trajektori optimum 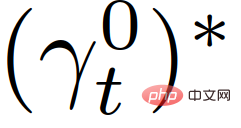 , kenderaan menggunakan input kawalan
, kenderaan menggunakan input kawalan 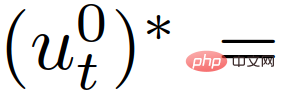
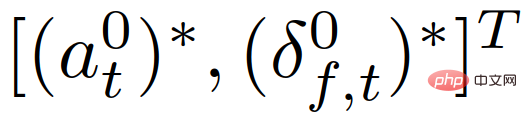 sepadan dengan trajektori untuk mengemas kini statusnya dalam tempoh pensampelan, dan kemudian dalam seterusnya Ulang langkah di atas untuk satu masa pensampelan segera t+1.
sepadan dengan trajektori untuk mengemas kini statusnya dalam tempoh pensampelan, dan kemudian dalam seterusnya Ulang langkah di atas untuk satu masa pensampelan segera t+1.
03 Model teori permainan tingkah laku koperatif kenderaan dan perwakilan eksplisit menggunakan pembelajaran tiruan
Bahagian ini memperkenalkan Ketua- model permainan pengikut yang digunakan dalam artikel ini. Untuk memudahkan pengiraan dalam talian model teori permainan, pembelajaran tiruan digunakan untuk mendapatkan model eksplisit berdasarkan rangkaian saraf untuk meramalkan dalam talian trajektori tindak balas kenderaan interaktif untuk bergabung ke dalam tingkah laku kenderaan sendiri dalam keseluruhan berasaskan MPC strategi perancangan trajektori.
Model Teori Permainan Pemimpin-Pengikut
Dalam kertas kerja ini, kami menganggap kepimpinan berasaskan pasangan Satu model teori parametrik interaksi ketua-pengikut digunakan untuk mewakili niat kerjasama pemandu dan tingkah laku kenderaan yang terhasil, yang dipanggil model permainan ketua-pengikut. Dalam model ini, kenderaan (atau pemandu) yang memutuskan untuk terus mendahului kenderaan lain ialah ketua pasangan itu, manakala kenderaan yang memutuskan untuk mengalah kepada kenderaan lain ialah pengikut pasangan itu. Pemimpin dan pengikut menggunakan strategi membuat keputusan yang berbeza. Model teori permainan pemimpin-pengikut ini pada asalnya dicadangkan dalam [32]. Model teori permainan ini dikaji secara ringkas di sini untuk memperkenalkan aplikasinya dalam senario gabungan lebuh raya paksa.
menunjukkan bahawa trajektori pemimpin dan pengikut adalah jumlah masing-masing, di mana jumlah ialah set trajektori yang boleh dilaksanakan bagi pemimpin dan pengikut. Andaikan bahawa kedua-dua pihak dalam permainan telah membuat keputusan untuk memaksimumkan ganjaran terkumpul mereka, masing-masing direkodkan sebagai dan , ditakrifkan seperti berikut:
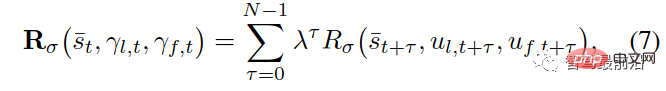
di mana mewakili peranan dalam permainan , ialah fungsi ganjaran ketua/pengikut, dan mewakili input kawalan yang sepadan dengan jumlah trajektori mereka.
Secara khusus, kami memodelkan proses membuat keputusan interaktif pemimpin dan pengikut seperti berikut:
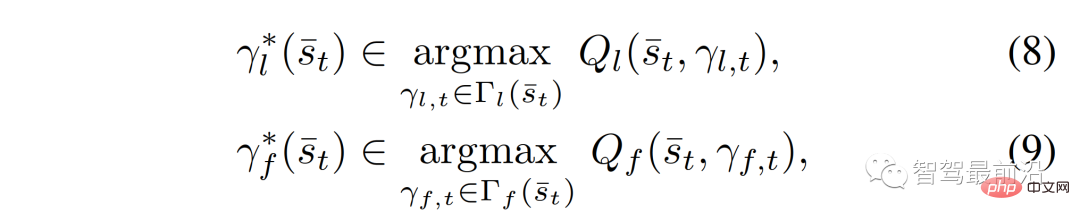
di mana 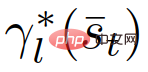 (berbeza daripada
(berbeza daripada 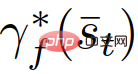 ) ialah trajektori optimum pemimpin (berbeza daripada pengikut), bergantung pada status trafik semasa,
) ialah trajektori optimum pemimpin (berbeza daripada pengikut), bergantung pada status trafik semasa,  dan
dan 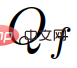 ditakrifkan seperti berikut:
ditakrifkan seperti berikut:
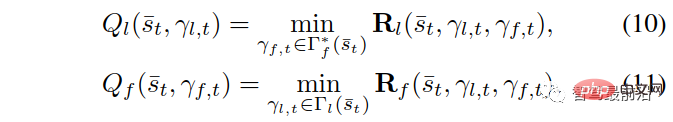
Antaranya
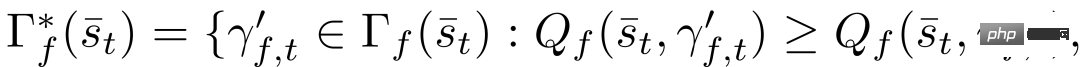
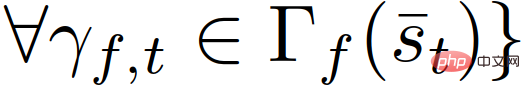 .
.
Model keputusan (8)-(11) dalam gabungan paksa boleh dijelaskan sebagai: seorang pengikut mewakili pemandu yang berniat untuk mengalah. Disebabkan ketidakpastian tentang tindakan pemandu lain, pengikut memutuskan untuk mengambil tindakan yang memaksimumkan ganjaran kes terburuk mereka melalui (9) dan (11), dengan mengandaikan bahawa pemandu lain bebas bertindak. Seorang pemimpin mewakili pemandu yang berhasrat untuk meneruskan, dengan mengandaikan pemandu lain akan mengalah. Oleh itu, pemimpin menggunakan model pengikut untuk meramalkan tindakan pemandu lain dan, melalui (8) dan (10), memaksimumkan ganjaran pemimpin itu sendiri memandangkan tindakan pengikut yang diramalkan. Model permainan ketua-pengikut ini sebahagiannya berasal daripada model permainan Stackelberg [38], tetapi mengendurkan beberapa andaian yang tidak digunakan untuk interaksi pemandu. Rujukan boleh dibuat kepada [32] untuk pemahaman yang lebih terperinci tentang model permainan ketua-pengikut dan keberkesanannya dalam memodelkan interaksi pemandu dalam senario berbilang kenderaan.
Sila ambil perhatian bahawa model ini tidak membayangkan bahawa kenderaan peneraju sentiasa memaksa kenderaan yang digabungkan untuk bergabung di belakangnya atau bahawa kenderaan pengikut sentiasa memaksa kenderaan yang digabungkan untuk bergabung di hadapannya, dalam berikutan dua contoh, kenderaan penggabungan mungkin bercantum di hadapan kenderaan pendahulu: 1) Kenderaan penggabungan berada di hadapan kenderaan pendahulu, dengan jarak yang cukup besar untuk membolehkan penggabungan selamat. 2) Kenderaan yang bergabung hampir sampai ke penghujung lorongnya. Kerana meninggalkan jalan mengakibatkan penalti yang besar (lihat Seksyen 2-c), selagi penggabungan kenderaan sendiri tidak mengakibatkan perlanggaran (penalti untuk perlanggaran lebih besar daripada meninggalkan jalan raya), kenderaan sendiri boleh memilih untuk bergabung sebelum kenderaan yang datang untuk mengelakkan perlanggaran besar,.
Di atas menunjukkan bahawa dalam model membuat keputusan (8)-(11), peranan pemimpin dan pengikut tidak diberikan oleh kedudukan ruang kenderaan (pemimpin adalah tidak semestinya kenderaan di hadapan). Di samping itu, model itu membolehkan kenderaan sendiri memaksa aliran trafik lorong sasaran untuk bergabung: apabila kenderaan sendiri menghampiri lorong sasaran, ia akan semakin memilih untuk bergabung untuk mengelak daripada dikenakan penalti kerana meninggalkan jalan raya kenderaan sendiri akan berada di lorong sasaran Mereka semua adalah pemimpin atau mereka masih mengambil tindakan penggabungan apabila jurang penggabungan semasa tidak cukup besar dan penggabungan tidak cukup selesa. Model (8)-(11) menunjukkan bahawa identiti peneraju kenderaan yang berinteraksi boleh meramalkan motivasi penggabungan kenderaan yang seterusnya. Selepas itu, demi keselamatan dan keselesaan mereka sendiri, kenderaan yang bergabung juga akan memperlahankan dan melebarkan jarak antara mereka untuk memastikan gabungan.
Pemimpin yang secara eksplisit mewakili strategi permainan melalui pembelajaran tiruan
(8)-(11) Kebolehan memandu berdasarkan Niat pemandu dan maklumat status trafik semasa boleh digunakan untuk meramalkan pembuatan keputusan dan trajektori kenderaan lain, iaitu strategi tindakan optimum pemimpin dan strategi tindakan optimum pengikut boleh diperoleh melalui (8)-(11) . Walau bagaimanapun, pengiraan dalam talian berulang (8)-(11) akan memakan masa. Oleh itu, kami akan menggunakan pembelajaran peniruan untuk mewakili dan secara eksplisit.
Merujuk kepada [39], kami menggunakan perwakilan pembelajaran terselia (khususnya menggunakan pembelajaran tiruan).
Pembelajaran meniru ialah masalah pembelajaran yang diselia di mana ejen mempelajari dasar dengan memerhati tingkah laku pakar. Pakar boleh menjadi agen kecerdasan buatan atau buatan, dan dalam kerja kami, apa yang diperolehi oleh (8)-(11) ialah strategi pakar.
Kami memperoleh strategi simulasi menggunakan algoritma "pengagregatan set data" [40].
Antaranya, matlamat pembelajaran keseluruhan algoritma pengagregatan set data boleh digambarkan sebagai:
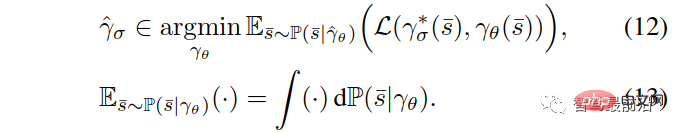
dinyatakan menggunakan strategi berparameter θ (Berat rangkaian saraf), mewakili fungsi kehilangan, lihat [39] dan [40] untuk butiran tentang pembelajaran tiruan dan algoritma "pengagregatan set data".
Strategi pembelajaran tiruan pembelajaran (8)-(11) boleh meramalkan trajektori pembuatan keputusan dan pembangunan masa depan keretanya sambil memahami niat kerjasama pemandu. Walau bagaimanapun, dalam senario lalu lintas tertentu, kita mungkin tidak mengetahui terlebih dahulu niat kerjasama pemandu lain kerana niat pemandu bukan sahaja bergantung pada keadaan lalu lintas (cth., kedudukan relatif dan kelajuan antara kedua-dua kenderaan) tetapi juga pada gaya pemandu /genre. Kami memodelkan ketidakpastian niat koperasi kenderaan lain sebagai pembolehubah terpendam, yang akan digunakan untuk menganggarkan niat koperasi kenderaan lain dan menggunakan kaedah kawalan ramalan untuk mendapatkan trajektori optimum dalam masalah perancangan dan kawalan kenderaan autonomi.
04 Pembuatan keputusan di bawah ketidakpastian niat kerjasama
Di bawah kami menerangkan lebuh raya di bawah ketidakpastian niat kerjasama Algoritma keputusan penggabungan paksa , pengawal permainan pemimpin-pengikut (LFGC). Semasa proses penggabungan paksa, kami menjana anggaran niat kerjasama pemandu lain seperti yang diterangkan dalam bahagian ini, berdasarkan yang kami modelkan (6) sebagai strategi kawalan berbilang kenderaan interaktif berpasangan.
Menganggar niat kerjasama kenderaan berinteraksi
Menggunakan permainan pengikut terpandu, berdasarkan kerjasama dengan pemandu kenderaan lain Permodelan tingkah laku dengan niat. Kenderaan yang menghasilkan dimodelkan sebagai pengikut dalam permainan, dan kenderaan yang berterusan (tanpa mengalah) dimodelkan sebagai pemimpin. Iaitu, niat kerjasama kenderaan interaktif boleh dianggarkan dengan menganggarkan peranannya dalam permainan ketua-pengikut.
Untuk mencapai matlamat ini, kami mempertimbangkan model dinamik trafik (2) dan tindakan optimum ketua atau pengikut (8) dan (9). Dari perspektif kenderaan sendiri, kenderaan interaktif memainkan permainan ketua-pengikut, dan model trafik dinamik boleh ditulis sebagai
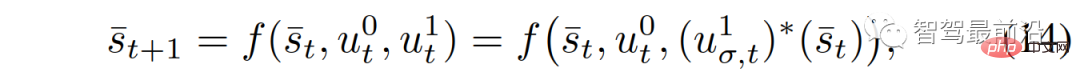
di mana 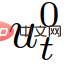 ialah kawalan kenderaan sendiri,
ialah kawalan kenderaan sendiri, 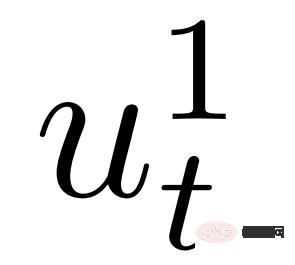 ialah kawalan kenderaan interaktif, yang diperolehi oleh ketua -permainan pengikut,
ialah kawalan kenderaan interaktif, yang diperolehi oleh ketua -permainan pengikut,  {leader, follower} mewakili pengikut atau ketua, dan
{leader, follower} mewakili pengikut atau ketua, dan 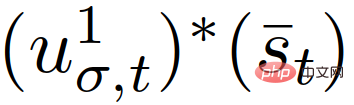 ialah input kawalan pertama, sepadan dengan
ialah input kawalan pertama, sepadan dengan 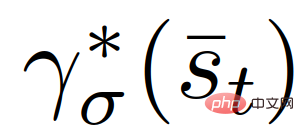 dalam (8) (9) trajektori optimum. Kini satu-satunya input kepada (14) ialah kawalan kenderaan sendiri
dalam (8) (9) trajektori optimum. Kini satu-satunya input kepada (14) ialah kawalan kenderaan sendiri  .
.
Memandangkan pada hakikatnya, pembuatan keputusan kereta lain tidak semestinya mengikut strategi optimum yang dikira dari (8) dan (9), jadi bunyi Gaussian ditambah, dengan mengandaikan Sistem berfungsi mengikut (14):
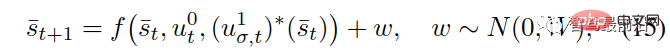
di manakah bunyi Gaussian aditif dengan min sifar dan kovarians.
Anggapkan bahawa kereta sendiri mempunyai kepercayaan terdahulu tentang σ, dinyatakan sebagai, di mana {pemimpin, pengikut}. Kemudian berdasarkan semua keadaan lalu lintas sebelumnya dan semua tindakan yang diambil oleh kenderaan sendiri
Kenderaan sendiri perlu mengira atau mengekalkan kepercayaan posteriori tentang peranan ketua atau pengikut kenderaan interaktif, 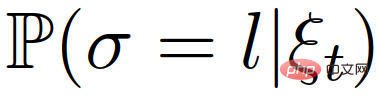 .
.
Menggunakan algoritma anggaran hibrid yang dicadangkan dalam [41], kepercayaan posterior bersyarat bagi peranan ketua atau pengikut kenderaan interaktif boleh dikira.
Secara khusus, mengenal pasti peranan pemimpin atau pengikut kenderaan interaktif boleh dinyatakan sebagai:
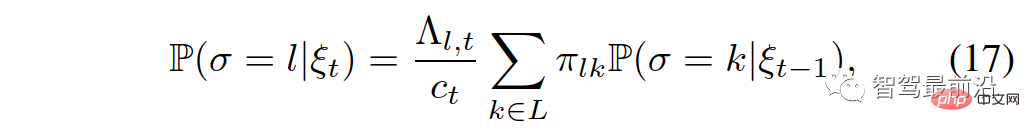
di mana  ialah kebarangkalian bersyarat; Kebarangkalian peralihan
ialah kebarangkalian bersyarat; Kebarangkalian peralihan  ;
; 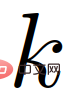 ialah fungsi kemungkinan bagi watak kenderaan tindakan
ialah fungsi kemungkinan bagi watak kenderaan tindakan 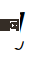 , ditakrifkan sebagai:
, ditakrifkan sebagai: 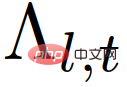
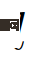
Dalam formula, 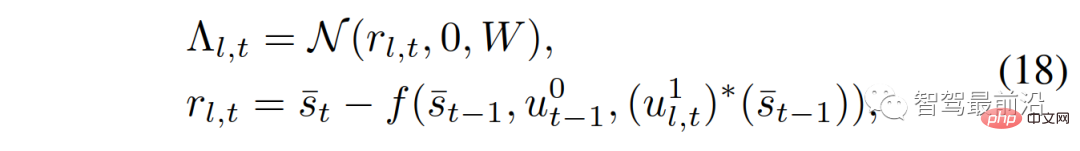
; 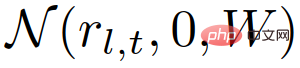
 ialah pemalar penormalan.
ialah pemalar penormalan. 
Diandaikan bahawa peranan kenderaan yang berinteraksi kekal tidak berubah semasa penggabungan, iaitu apabila
, apabila 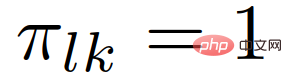
 , kepercayaan posterior peranan ketua atau pengikut kenderaan interaktif boleh dikemas kini menggunakan persamaan berikut:
, kepercayaan posterior peranan ketua atau pengikut kenderaan interaktif boleh dikemas kini menggunakan persamaan berikut: 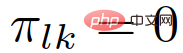
di mana 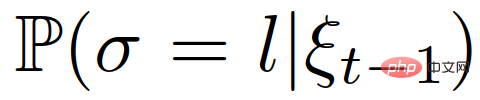 ialah kepercayaan terdahulu dalam peranan pemimpin atau pengikut kenderaan interaktif.
ialah kepercayaan terdahulu dalam peranan pemimpin atau pengikut kenderaan interaktif.
Strategi kawalan untuk interaksi berbilang kenderaan
Apabila lalu lintas sesak, mungkin terdapat Berbilang kenderaan mengganggu penggabungan kenderaan anda sendiri, seperti yang ditunjukkan dalam Rajah 1. Penyelesaian kerumitan rendah adalah untuk kenderaan sendiri hanya mempertimbangkan interaksi dengan kenderaan pertama, dan kemudian mula berinteraksi dengan kenderaan kedua selepas kenderaan pertama bergerak pergi. Walau bagaimanapun, ini boleh menyebabkan kelewatan dalam menganggar niat kenderaan berikut, menyebabkan kenderaan sendiri kehilangan peluang untuk bergabung.
Penyelesaian lain ialah berinteraksi dengan berbilang kenderaan pada masa yang sama. Pada masa ini, model perlu dibina untuk meramalkan tingkah laku kenderaan interaktif itu. Walaupun permainan ketua-pengikut 2-pemain yang diterangkan dalam Bahagian 3 boleh diperluaskan kepada permainan ketua-pengikut berbilang pemain dengan mempertimbangkan hierarki membuat keputusan berbilang peringkat, kerumitan model akan berkembang secara eksponen apabila bilangan pemain meningkat. Apabila terdapat lebih daripada 3 pemain, sukar untuk mendapatkan keseimbangan Stackelberg [42]. Oleh itu, kami mencadangkan kaedah yang boleh dikendalikan secara pengiraan untuk melanjutkan rangka kerja kepada interaksi berbilang kenderaan dengan mempertimbangkan interaksi berpasangan.
Apabila terdapat m kenderaan yang berinteraksi, kami mempertimbangkan interaksi berpasangan antara kenderaan sendiri dan setiap kenderaan berinteraksi, dan kemudian membina m kenderaan yang mengandungi kereta sendiri dan kth yang lain Trafik keadaan keadaan kenderaan dinyatakan sebagai , dan model dinamik setiap satu diberikan oleh:
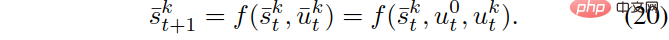
Begitu juga , kita boleh menggunakan 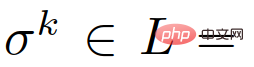 {leader, follower} untuk mewakili pemimpin berpasangan atau peranan pengikut kenderaan interaktif ke-k, dan menggunakan
{leader, follower} untuk mewakili pemimpin berpasangan atau peranan pengikut kenderaan interaktif ke-k, dan menggunakan 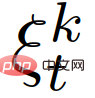 untuk mewakili Set semua keadaan lalu lintas berpasangan sebelumnya dan tindakan kenderaan sendiri, iaitu,
untuk mewakili Set semua keadaan lalu lintas berpasangan sebelumnya dan tindakan kenderaan sendiri, iaitu,
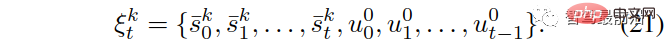
kemudian Kami boleh menggunakan (19) untuk mengemas kini kepercayaan setiap peranan ketua atau pengikut kenderaan yang berinteraksi, 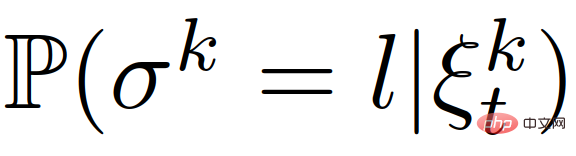 ,
, 
{leader , follower}. Strategi kawalan berasaskan MPC dalam (6) boleh dinyatakan semula sebagai:
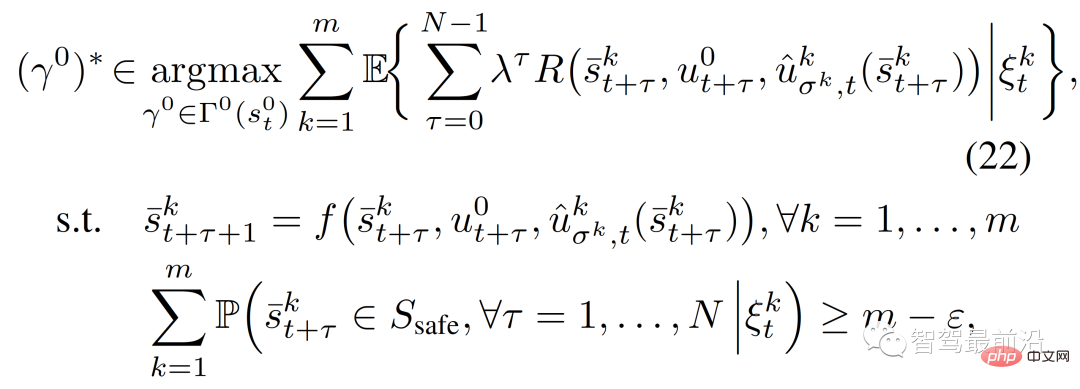
di mana, 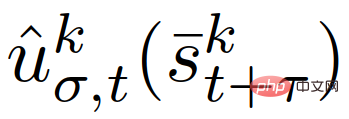 ialah input kawalan pertama yang sepadan dengan trajektori strategi latihan
ialah input kawalan pertama yang sepadan dengan trajektori strategi latihan 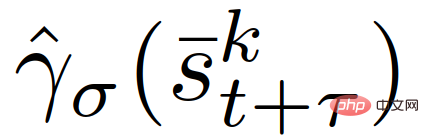 dalam (12), dan ε∈[0,1] mewakili (ditentukan pengguna ) yang diperlukan Kekangan memenuhi tahap kebarangkalian.
dalam (12), dan ε∈[0,1] mewakili (ditentukan pengguna ) yang diperlukan Kekangan memenuhi tahap kebarangkalian.
Jangkaan dalam fungsi objektif boleh diselesaikan mengikut (23);
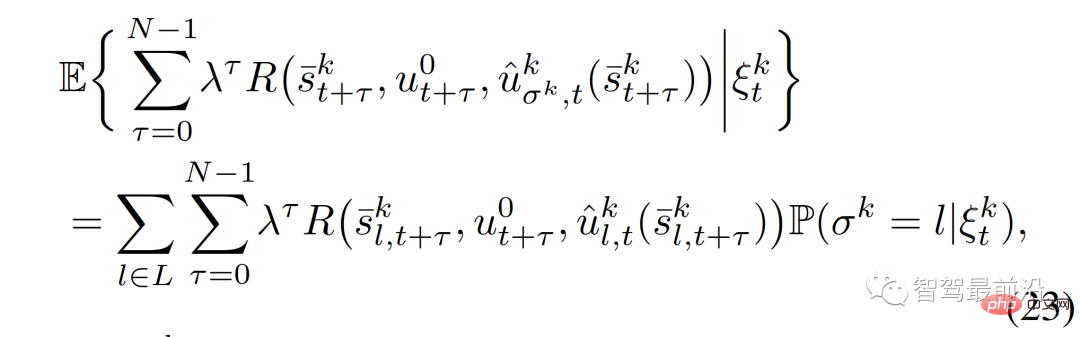
di mana, 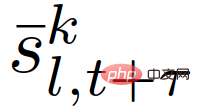 ialah peranan kenderaan interaktif yang diberikan sebagai
ialah peranan kenderaan interaktif yang diberikan sebagai 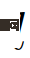 , manakala kekangan terakhir dalam (22) boleh melepasi,
, manakala kekangan terakhir dalam (22) boleh melepasi,
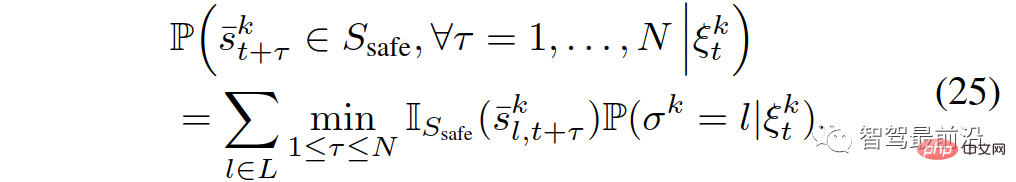
Di mana, 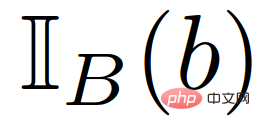 ialah fungsi penunjuk b dalam set B. Ambil perhatian bahawa kekangan terakhir dalam (22) menguatkuasakan syarat berikut,
ialah fungsi penunjuk b dalam set B. Ambil perhatian bahawa kekangan terakhir dalam (22) menguatkuasakan syarat berikut,
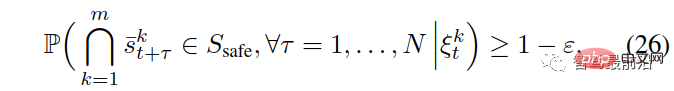
yang bermaksud bahawa sebarang interaksi berpasangan memasuki keadaan tidak selamat (cth., kebarangkalian perlanggaran dan meninggalkan sempadan jalan) adalah kurang daripada ε.
Untuk mendapatkan (26), kita mula-mula menandakan peristiwa 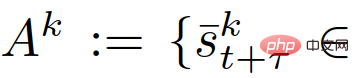
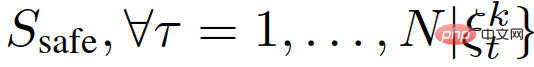 dan kemudian
dan kemudian
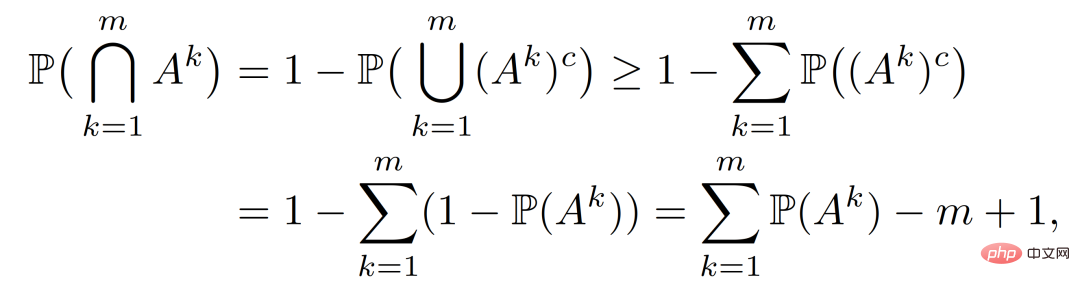
Kemudian menggunakan kekangan terakhir dalam (22), kita boleh mendapatkan
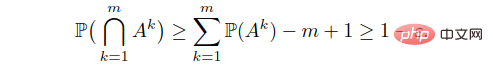
Perbezaan utama antara (6) dan (22) ialah:
1) dalam (6) tidak diketahui, manakala dalam (22) ) , ia diperoleh berdasarkan strategi latihan pembelajaran tiruan; , untuk menerangkan kepercayaan kebarangkalian peranan pemimpin/pengikut bagi kenderaan interaktif; berbilang kenderaan Tingkah laku yang tidak menentu (mudah untuk dikira);
Algoritma membuat keputusan berjalan seperti berikut: pada masa pensampelan t, kenderaan sendiri mengukur keadaan semasa setiap pasangan interaktif dan menambahkannya bersama-sama dengan input kawalan sebelumnya pada vektor pemerhatian 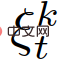 Sederhana. Kepercayaan tentang peranan ketua atau pengikut setiap kenderaan dikemas kini mengikut (19). Kemudian, menggunakan strategi kawalan berasaskan MPC (22), trajektori optimum
Sederhana. Kepercayaan tentang peranan ketua atau pengikut setiap kenderaan dikemas kini mengikut (19). Kemudian, menggunakan strategi kawalan berasaskan MPC (22), trajektori optimum 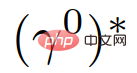 diperoleh dengan mencari semua trajektori yang diperkenalkan dalam Bahagian 2-D, dan kenderaan sendiri menggunakan Kawalan pertama input kepada mengemas kini keadaannya. Keseluruhan proses akan diulang apabila sampel diambil seterusnya.
diperoleh dengan mencari semua trajektori yang diperkenalkan dalam Bahagian 2-D, dan kenderaan sendiri menggunakan Kawalan pertama input kepada mengemas kini keadaannya. Keseluruhan proses akan diulang apabila sampel diambil seterusnya.
Perlu diambil perhatian bahawa strategi kawalan (22) adalah "sedar interaksi" atas sebab-sebab berikut:
1 ) Ia Berdasarkan model teori permainan ketua-pengikut (8)-(11), ramalkan trajektori kereta lain di bawah niat interaksi yang berbeza.
2) Ramalan ini adalah gelung tertutup. Khususnya, sepadan dengan perancangan trajektori berbeza bagi kenderaan sendiri 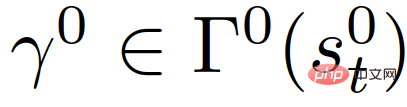 , ramalan trajektori kenderaan lain dengan niat tertentu juga berbeza. Keadaan ini adalah kerana kelakuan ramalan kenderaan lain bergantung pada keadaan trafik, dan keadaan trafik yang diramalkan bergantung pada trajektori yang dirancang bagi kenderaan sendiri.
, ramalan trajektori kenderaan lain dengan niat tertentu juga berbeza. Keadaan ini adalah kerana kelakuan ramalan kenderaan lain bergantung pada keadaan trafik, dan keadaan trafik yang diramalkan bergantung pada trajektori yang dirancang bagi kenderaan sendiri.
3) Fungsi objektif dalam (22) ialah jangkaan bersyarat, dan kekangan yang mewakili keselamatan ialah kebarangkalian bersyarat, kedua-duanya adalah berdasarkan kereta lain ' niat (iaitu pemimpin atau pengikut), 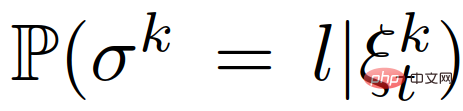 . Pada masa yang sama, niat kereta lain dianggarkan berdasarkan tingkah laku interaksinya sebelum ini.
. Pada masa yang sama, niat kereta lain dianggarkan berdasarkan tingkah laku interaksinya sebelum ini.
05 Simulasi dan Keputusan Pengesahan
Dalam bahagian ini, kami akan membentangkan Leader-Following Game Controller (LFGC) ) ) digunakan pada keputusan pengesahan masalah penggabungan paksa kenderaan autonomi. Kami secara khusus mempertimbangkan tiga pengesahan simulasi di mana LFGC menganggap bahawa kenderaan berinteraksi memainkan permainan ketua-pengikut dengan kenderaan sendiri dan menganggarkan peranan ketua/pengikut mereka dalam permainan. Kami juga menganggap bahawa sebaik sahaja memasuki situasi pertukaran lorong paksa, kenderaan sendiri menggunakan isyarat membelok untuk menjajarkan dengan lorong, mengumumkan hasratnya untuk bergabung dan memulakan proses gabungan paksa. Oleh itu, kenderaan lain yang berinteraksi antara satu sama lain akan menyedari niat kenderaan sendiri untuk bergabung dan bertindak balas dengan sewajarnya.
Kami mula-mula mengesahkan LFGC dalam permainan ketua-pengikut menggunakan kenderaan interaktif yang dikawal oleh sama ada ketua atau pengikut. Kami kemudiannya menguji LFGC dengan kenderaan interaktif yang dikawal oleh jenis pemandu lain atau data trafik sebenar. Tambahan pula, kami menguji kes di mana kenderaan interaktif (IDM) dikawal oleh model pemandu pintar dan kenderaan interaktif mengikuti data trafik Lebuhraya AS 101 sebenar dari Tapak Simulasi Generasi Seterusnya [34]. Simulasi kami telah dilakukan pada platform MATLAB R2019a pada PC dengan Intel Xeon E3-1246 v3 @ 3.50 GHz CPU dan memori 16 GB.
Kenderaan Interaksi Model Pemimpin-Pengikut
Mula-mula kita mensimulasikan dan mengawal interaksi menggunakan Kenderaan ketua/pengikut, uji LFGC. Senario yang kami pertimbangkan ditunjukkan dalam Rajah 4. Kenderaan autonomi (biru) di lorong pecutan perlu bergabung ke lebuh raya sebelum penghujung lorong pecutan, manakala banyak kenderaan lain (merah, merah jambu, hijau) sedang berada di lebuh raya. Seperti yang ditunjukkan dalam Rajah 4, kenderaan sendiri memulakan proses penggabungan paksa dengan melencong ke arah tanda lorong dan memancarkan isyarat belok. Dalam kes ini, kenderaan autonomi perlu berinteraksi dengan kenderaan lain untuk mencapai gabungan yang selamat.
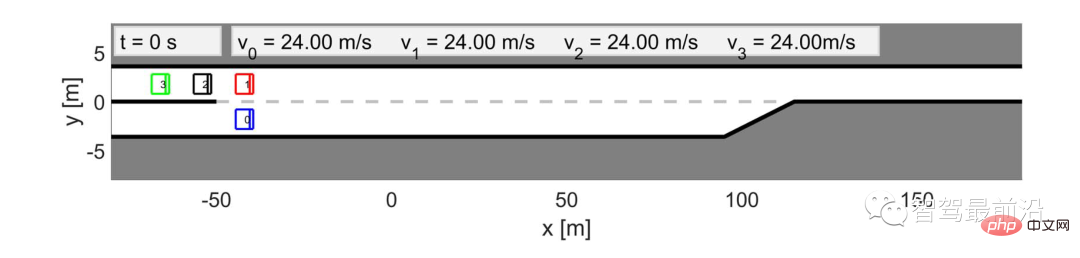
Rajah 4 rajah senario pengesahan LFGC bagi ketua/pengikut mengawal kenderaan interaktif dalam senario gabungan lebuh raya paksa
Selepas ujian, Keupayaan Kereta = betul mengenali niat kenderaan interaktif (iaitu, ia boleh mengklasifikasikan kenderaan interaktif dengan betul sebagai ketua/pengikut)
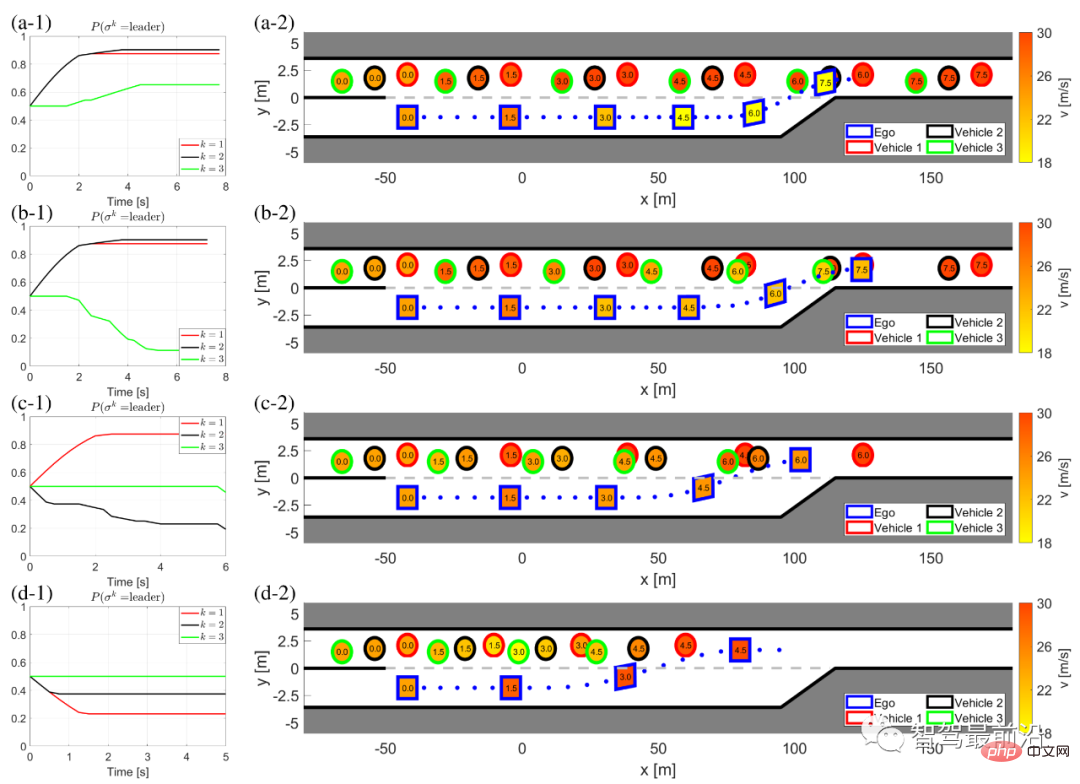
Rajah 5 Hasil interaksi kereta lain yang menggunakan LFGC dengan kombinasi pemimpin dan pengikut yang berbeza
(a) Kereta lain mempunyai tiga ketua; >
(b) Kereta yang satu lagi ialah 1 ketua (kenderaan 1) dan 2 pengikut (kenderaan 2 dan 3); pemimpin (kenderaan 1 dan 2) dan seorang pengikut (kenderaan 3);(d) Kereta yang satu lagi mempunyai tiga pengikut.
Lajur kiri (a-1) hingga (d-1) menunjukkan kepercayaan kereta sendiri terhadap ketua keretanya dalam permainan. Lajur kanan (a-2) hingga (d-2) menunjukkan hasil sejarah masa tingkah laku kenderaan sendiri dan kenderaan lain semasa proses penggabungan paksa ini. Khususnya, dalam lajur kanan, warna garis sempadan setiap blok membezakan kenderaan yang berbeza, nombor dalam blok mewakili masa dalam saat, warna setiap blok menggambarkan kelajuan kenderaan pada masa itu dan garis titik biru mewakili trajektori kenderaan sendiri. Ambil perhatian bahawa kenderaan 1-3 mempunyai kedudukan membujur yang sama, beberapa offset membujur telah ditambahkan pada angka untuk pembezaan yang lebih baik.
Untuk LFGC, skop perancangan ialah N = 4 dan parameter kekangan peluang ialah ε = 0.1. Ambil perhatian bahawa N yang lebih besar boleh menghasilkan prestasi jangka panjang yang lebih baik tetapi juga masa pengiraan yang lebih lama, manakala N yang lebih kecil mungkin menekankan faedah segera dan dengan itu tidak digabungkan dalam banyak kes. Untuk gabungan lebuh raya paksa yang dipertimbangkan dalam artikel ini, N secara amnya perlu dipilih supaya ia melebihi tempoh pertukaran lorong (iaitu
).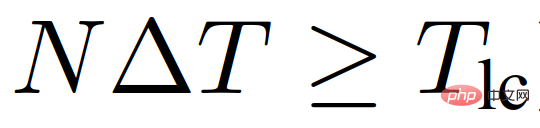 Rajah 5(a) menunjukkan keputusan apabila kereta ego itu berinteraksi dengan tiga ketua. Kenderaan sendiri mampu menangkap niat kenderaan yang berinteraksi, iaitu, semua kenderaan lebih berkemungkinan untuk menjadi pemimpin dalam permainan, seperti yang ditunjukkan dalam Rajah 5(a-1). Selepas mendapat maklumat ini, kenderaan sendiri memutuskan untuk memperlahankan selepas t = 1 [s] dan menunggu untuk bergabung selepas semua kenderaan yang berinteraksi berlalu.
Rajah 5(a) menunjukkan keputusan apabila kereta ego itu berinteraksi dengan tiga ketua. Kenderaan sendiri mampu menangkap niat kenderaan yang berinteraksi, iaitu, semua kenderaan lebih berkemungkinan untuk menjadi pemimpin dalam permainan, seperti yang ditunjukkan dalam Rajah 5(a-1). Selepas mendapat maklumat ini, kenderaan sendiri memutuskan untuk memperlahankan selepas t = 1 [s] dan menunggu untuk bergabung selepas semua kenderaan yang berinteraksi berlalu.
Dalam kes ini, kenderaan ego memerhati kenderaan 1 dan 2 memecut tanpa mengalah, jadi kenderaan ego memutuskan untuk memperlahankan dan bergabung antara kenderaan 2 dan 3. Kami juga menjalankan ujian apabila kereta kendiri berinteraksi dengan tiga pengikut, dan hasilnya ditunjukkan dalam Rajah 5(d). Purata masa pengiraan untuk menyelesaikan (22) ialah 0.182 [s] dalam setiap langkah masa.
Untuk semua kes yang ditunjukkan dalam Rajah 5, kepercayaan yang dimulakan adalah sama, yang bermaksud bahawa ego tidak mengetahui terlebih dahulu sama ada kenderaan interaktif itu adalah pemimpin atau pengikut. Oleh itu, kenderaan ego bergantung pada pemerhatiannya untuk menganggarkan peranan pemimpin/pengikut vektor interaksi. Dalam permainan ketua-pengikut, apabila semua kenderaan interaktif dikawal oleh ketua/pengikut, LFGC boleh menangkap niat kenderaan interaktif dan membuat keputusan yang sepadan.
Kereta lain menggunakan model IDM
jenis interaksi Keputusan pengesahan yang ditunjukkan dalam Bahagian 5-A mengandaikan bahawa kereta lain membuat keputusan berdasarkan permainan ketua-pengikut. LFGC menganggarkan peranan pemandu lain dalam permainan dan membuat keputusan sewajarnya. Ini bermakna persekitaran dalam Bahagian 5-A berkelakuan seperti yang diharapkan oleh LFGC. Walau bagaimanapun, tingkah laku sebenar pemandu lain mungkin berbeza daripada dasar permainan ketua-pengikut. Oleh itu, kami terus menyiasat cara rangka kerja bertindak balas apabila kenderaan lain menggunakan Model Pemandu Pintar (IDM). Dalam bahagian ini, gunakan IDM untuk mengawal kereta lain dan berinteraksi dengan kereta anda sendiri. Kenderaan ego masih dikawal oleh LFGC dan cuba untuk menganggarkan niat kenderaan berinteraksi dengan menganggarkan peranan pemimpin atau pengikut mereka yang sepadan. IDM ialah model penjejakan kereta masa berterusan, ditakrifkan oleh (27) hingga (29) [43]. 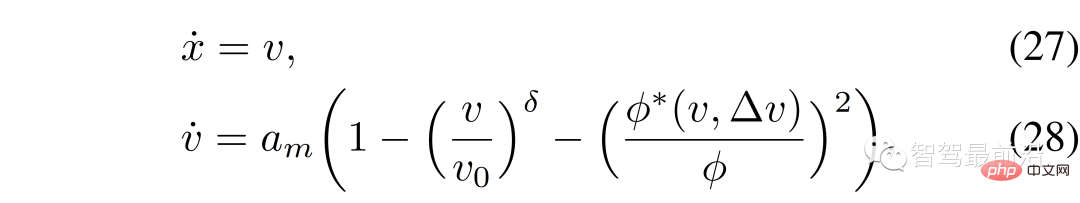
di mana 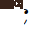 ialah kedudukan menegak; > ialah kelajuan membujur;
ialah kedudukan menegak; > ialah kelajuan membujur; 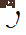 ialah kelajuan yang dijangkakan bagi kenderaan; 🎜>
ialah kelajuan yang dijangkakan bagi kenderaan; 🎜>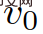 ialah kedudukan kenderaan sasaran,
ialah kedudukan kenderaan sasaran, 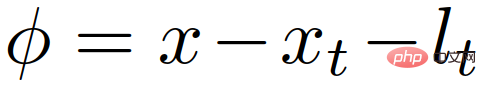 ialah panjang kenderaan sasaran;
ialah panjang kenderaan sasaran;
ialah perbezaan kelajuan antara kenderaan dan kenderaan sasaran ; 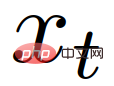
 Berdasarkan:
Berdasarkan: 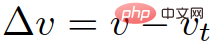

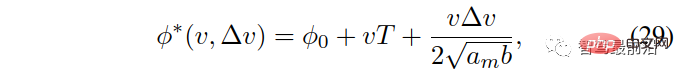 Di mana, ialah parameter bagi model IDM. Tafsiran fizikal parameter ini ialah pecutan maksimum
Di mana, ialah parameter bagi model IDM. Tafsiran fizikal parameter ini ialah pecutan maksimum
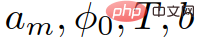 , masa T yang diingini dan nyahpecutan yang selesa b .
, masa T yang diingini dan nyahpecutan yang selesa b . 
Kami menganggap senario yang ditunjukkan dalam Rajah 6 sebagai ujian pengesahan. Dalam Rajah 6, semua kenderaan didahului oleh kenderaan lain (kenderaan hitam 4) yang bergerak pada kelajuan tetap. Kenderaan ego masih sama dengan bahagian V-A dan dikawal oleh LFGC, yang bermaksud bahawa dari perspektif kenderaan ego, ia bermain permainan ketua-pengikut dengan semua kenderaan yang berinteraksi. Bagi ketiga-tiga kenderaan yang berinteraksi ini (Kenderaan 1 hingga 3), ia dikawal oleh IDM, mengikut kenderaan sebelumnya (Kenderaan 4) atau kenderaan sendiri dengan masa pendahuluan tertentu t. Parameter model IDM disenaraikan dalam Jadual 1. Ambil perhatian bahawa kenderaan sendiri menganggap kenderaan 4 sebagai kenderaan persekitaran dan mengandaikan bahawa ia bergerak pada kelajuan tetap.
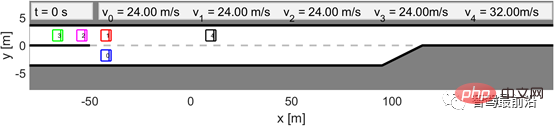
Rajah 6 Apabila kereta lain mengikut IDM, kereta sendiri menggunakan LFGC untuk melengkapkan adegan penggabungan paksa.
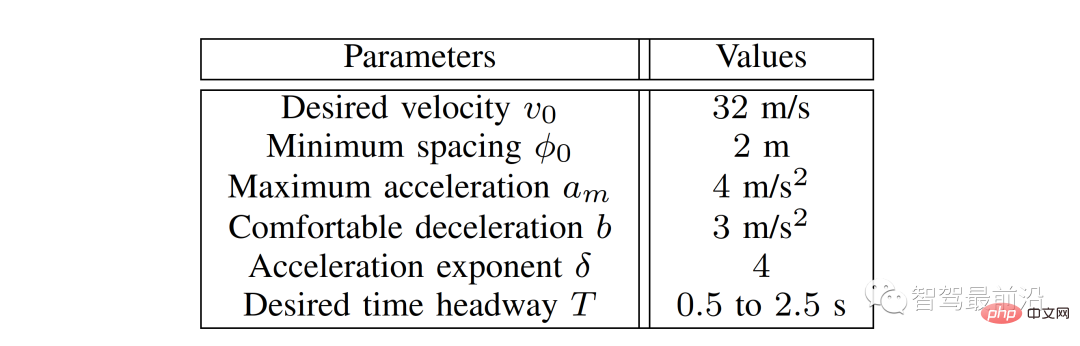
Jadual 1 Parameter model pemacu pintar
Gamb. 7 menunjukkan keputusan apabila kenderaan sendiri berinteraksi dengan kenderaan lain yang dikawal oleh IDM dengan kenderaan sasaran yang berbeza dan masa yang dikehendaki berbeza.
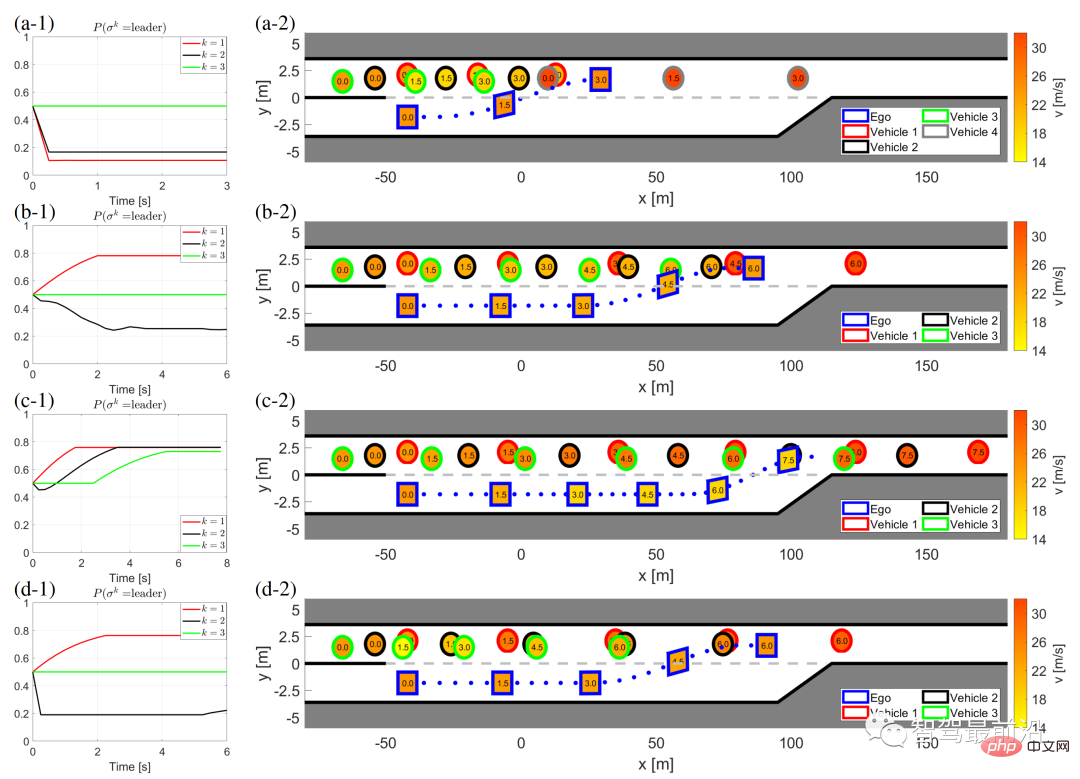
Rajah 7: Hasil interaksi LFGC untuk kereta lain dengan sasaran berbeza dan jangkaan masa yang dikawal oleh IDM
(a) Kenderaan 1 menjana (mengikut kenderaannya sendiri) kemajuan masa T = 1 [s], Kenderaan 2 dan Kenderaan 3 mengikuti T = 0.5 [s];
(b) Kenderaan 2 menjana (mengikut kenderaan sendiri) T = 0.5 [s], kenderaan 1 dan 3 mengikuti kenderaan sebelumnya T = 0.5 [s]
(c) Semua kenderaan mengikut kenderaan sebelumnya dengan T = 0.5 [s]; (d) Semua kenderaan mengikut kenderaan sebelumnya dengan T = 1.5 [s].
Lajur kiri (a-1) hingga (d-1) menunjukkan kepercayaan kereta sendiri terhadap ketua keretanya dalam permainan. Lajur kanan (a-2) hingga (d-2) menunjukkan hasil sejarah masa kelakuan diri dan kereta lain semasa proses penggabungan paksa ini. Khususnya, dalam lajur kanan, warna garis sempadan setiap blok membezakan kenderaan yang berbeza, nombor dalam blok mewakili masa dalam saat, warna setiap blok menggambarkan kelajuan kenderaan pada masa itu dan garis titik biru mewakili trajektori kenderaan sendiri.
Dalam Rajah 7(a), kenderaan interaktif pertama (kenderaan 1) berhasrat untuk menyerah kepada kenderaannya sendiri, jadi ia memilih untuk mengikut kenderaannya sendiri yang mara selama 1 saat, dan dua terakhir Kenderaan interaktif mengikuti kenderaan sebelumnya selama 0.5 saat. Seperti yang dapat dilihat dari Rajah 7 (a-1), kereta kendiri percaya bahawa kenderaan 1 mempunyai kebarangkalian tinggi untuk menjadi pengikut dalam permainan, dan memilih untuk bergabung di hadapan kenderaan 1, seperti yang ditunjukkan dalam Rajah 7 (a -2).
Rajah 7(b) menunjukkan satu lagi situasi, iaitu kenderaan interaktif pertama (kenderaan 1) mara 0.5, dan kenderaan interaktif kedua berhasrat untuk mengalah kepada kenderaannya sendiri dan maju 0.5 Ikut kereta sendiri. Jadi dalam kes ini, dari perspektif kenderaan sendiri, kenderaan 1 mempunyai kebarangkalian yang lebih tinggi untuk menjadi ketua dalam permainan, dan kenderaan 2 mempunyai kebarangkalian yang lebih tinggi untuk menjadi pengikut dalam permainan kenderaan sendiri Kereta berjaya bergabung di hadapan kenderaan 2.
Dua lagi kes bukan hasil ditunjukkan dalam Rajah 7(c) dan (d) Rajah 7(c) menunjukkan keputusan untuk semua kenderaan yang berinteraksi mengikut kenderaan sebelumnya. Dari perspektif kenderaan sendiri, semua kenderaan yang berinteraksi lebih berkemungkinan menjadi peneraju dalam permainan, jadi kereta sendiri boleh berjaya digabungkan selepas semua kenderaan berlalu.
Dalam Rajah 7(d), semua kenderaan yang berinteraksi bergerak ke hadapan pada kelajuan 1.5 saat. Dalam kes ini, kenderaan sendiri mendapati bahawa Kenderaan 2 berkelakuan secara konservatif dan percaya bahawa Kenderaan 2 mempunyai kebarangkalian yang lebih tinggi untuk menjadi pengikut dalam permainan. Oleh itu, kenderaan sendiri berjaya bergabung antara Kenderaan 1 dan Kenderaan 2. Purata masa pengiraan untuk menyelesaikan (22) ialah 0.198 [s] dalam setiap langkah masa.
Kenderaan lain mengikut data trafik sebenar
Kami telah menguji LFGC pada model kereta lain dan IDM yang dipandu pemimpin/pengikut dalam permainan pengikut-pengikut. Kami ingin menguji lagi prestasi pengawal menggunakan data trafik sebenar. Khususnya, kami menggunakan set data trafik Lebuhraya AS 101 daripada tapak web Simulasi Generasi Seterusnya (NGSIM) [34], yang dikumpulkan oleh Pentadbiran Lebuhraya Persekutuan AS dan dianggap sebagai salah satu sumber data pemanduan naturalistik yang terbesar. Dataset US Highway 101 telah dikaji secara meluas dalam literatur [44], [45], [46].
Secara lebih khusus, kami mempertimbangkan sebahagian daripada set data trafik US 101, yang mengandungi 30 minit trajektori kenderaan di lebuh raya US 101. Tempoh masa adalah dari 7:50 hingga 8:20 pagi, yang mewakili kesesakan sebelum dan selepas waktu sibuk pagi. Set data mengandungi trajektori kedudukan dan halaju serta dimensi kenderaan bagi kira-kira 6000 kenderaan, dengan maklumat direkodkan setiap 0.1 [s]. Pandangan atas bahagian Lebuhraya AS 101 yang digunakan untuk pengumpulan data ditunjukkan dalam Rajah 8. Segmen kajian termasuk lima lorong utama lebuh raya, tanjakan ke lebuh raya, tanjakan luar lebuh raya dan lorong tambahan untuk bergabung ke dan keluar dari lebuh raya.
Seperti yang dibincangkan dalam [47], set data US101 mengandungi sejumlah besar bunyi yang disebabkan oleh analisis video dan pembezaan berangka. Untuk mengatasi kelemahan ini, kami menggunakan penapis Savitsky-Gorey [48] untuk melicinkan kedudukan kenderaan dan mengemas kini halaju yang sepadan. Penapis Savitzky-Golay berfungsi dengan baik pada set data US101 dengan panjang tetingkap masa 21 [45]. Trajektori kenderaan asal dan trajektori kenderaan terlicin yang sepadan ditunjukkan dalam Rajah 9.
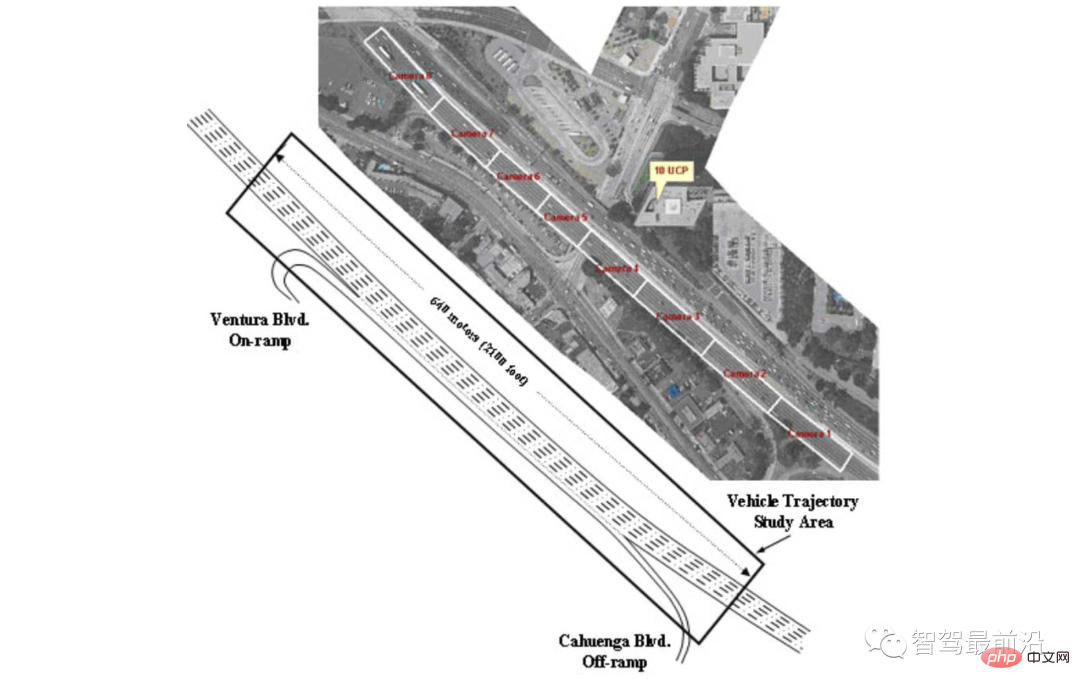
Rajah 8 Pandangan atas lebuh raya yang digunakan untuk mengumpul data trafik AS 101 [34]
Bahagian ini termasuk lima lorong utama lebuh raya, tanjakan ke lebuh raya, tanjakan keluar untuk keluar dari lebuh raya dan lorong Bantuan untuk bergabung ke dan keluar dari lebuh raya.
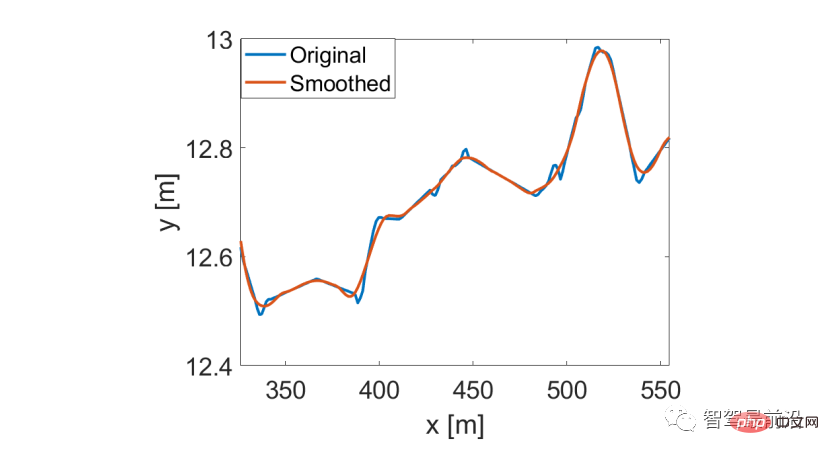
Rajah 9 Dilancarkan daripada set data trafik US 101 menggunakan penapis Savitsky-Gorey Trajektori Kenderaan
Untuk ujian pengesahan LFGC, kami menumpukan pada lorong atas tanjakan dan tambahan untuk mengenal pasti semua kenderaan yang bergabung. Selepas mengenal pasti kenderaan yang bergabung dan senario yang sepadan, kami mengenal pasti kenderaan yang berinteraksi mengikut Rajah 10. Secara khususnya, kami menganggap kenderaan pertama di lorong sasaran dalam tempoh 2 saat sebagai kenderaan berinteraksi pertama, dan kenderaan berturut-turut sebagai kenderaan kedua dan ketiga. Untuk semua kenderaan lain yang terdapat di tempat kejadian, kenderaan sendiri akan menganggapnya sebagai kenderaan alam sekitar dan menganggap bahawa mereka bergerak pada kelajuan yang tetap. Senario gabungan yang dikenal pasti ditunjukkan dalam Rajah 11.

Rajah 10 Pemilihan kenderaan interaktif: kereta sendiri (kenderaan biru) dengan kotak pilihan (kotak merah ) ialah kenderaan interaktif
Hujung hadapan kotak pilihan maju 2 kali sebelum kereta sendiri. Kenderaan pertama di lorong sasaran dalam kotak pilihan ialah kenderaan interaktif pertama, dan kenderaan berikut ialah kenderaan interaktif kedua dan ketiga. Untuk semua kenderaan lain di lebuh raya, ia dianggap sebagai kenderaan ambien dan diandaikan mengekalkan kelajuan yang tetap.
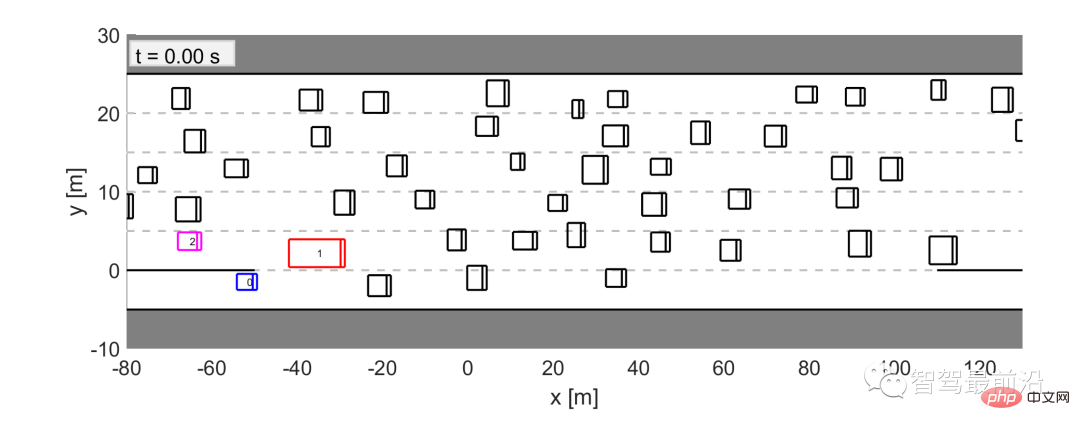
Rajah 11 Senario gabungan ditentukan daripada set data trafik US 101
Dalam senario ini, kenderaan 0 (kenderaan biru) ialah kenderaan yang digabungkan, dan kami membenarkan LFGC mengawal kenderaan 0. Mengikut kriteria kami untuk memilih kenderaan interaktif, kenderaan 1 (kenderaan merah) dan kenderaan 2 (kenderaan merah jambu) dipilih sebagai kenderaan interaktif, dan semua kenderaan lain (kenderaan hitam) dianggap sebagai kenderaan alam sekitar, dengan mengandaikan bahawa mereka memandu pada kelajuan tetap .
Untuk setiap senario yang digabungkan, bukannya membiarkan kenderaan sendiri menjejaki data trafik, kami menggunakan LFGC untuk mengawal tingkah laku kenderaan sendiri dan trajektori yang terhasil. Untuk semua kenderaan lain, termasuk kenderaan berinteraksi dan kenderaan persekitaran, ia mengikuti trajektori yang sepadan seperti yang dipaparkan dalam set data trafik AS 101. LFGC kemudiannya perlu menganggarkan niat kenderaan yang berinteraksi dan mengawal kenderaan sendiri untuk bergabung dengan sewajarnya. Ambil perhatian bahawa semasa pengumpulan data, kenderaan berinteraksi dan ambien mungkin berinteraksi dengan kenderaan yang digabungkan semasa trafik sebenar. Oleh kerana 1) LFGC mungkin bertindak secara berbeza daripada operasi manusia, tingkah laku kenderaan interaktif atau kenderaan persekitaran tidak bertindak balas kepada tingkah laku kenderaan sendiri. Sebaliknya, tingkah laku mereka ditentukan terlebih dahulu oleh set data trafik, jadi langkah konservatif perlu diambil untuk mengelakkan perlanggaran 2) Trafik padat, tidak meninggalkan margin selamat untuk kenderaan sendiri bergabung tanpa bersilang dengan kotak perlanggaran kenderaan lain.
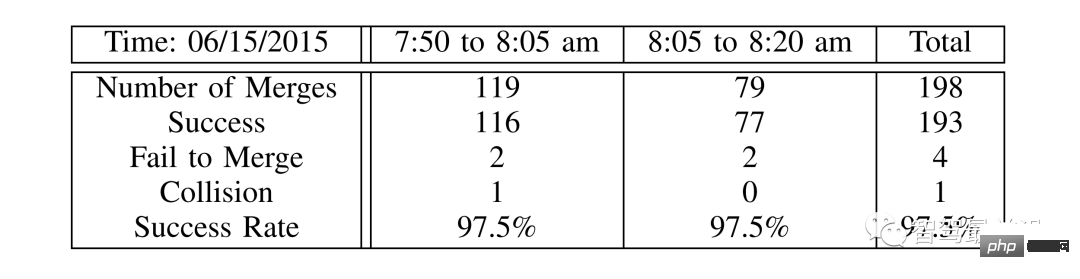
Jadual 2: Pengesahan statistik LFGC menggunakan set data trafik US101
"Kejayaan" bermaksud kenderaan sendiri berjaya bergabung ke lorong sasaran tanpa sebarang perlanggaran. "Gagal bergabung" bermaksud kenderaan sendiri tidak boleh bergabung di hujung lorong tambahan. "Perlanggaran" merujuk kepada perlanggaran antara kenderaan anda sendiri dengan kenderaan lain. Akhirnya, penulis mengambil tangkapan skrin proses penggabungan untuk analisis.
Dalam Rajah 12, kami menunjukkan tangkapan skrin gabungan yang berjaya. Dalam angka ini, kenderaan biru dikawal oleh LFGC, dan kotak kelabu mewakili kedudukan sebenar kenderaan sendiri dalam set data. Semua kenderaan lain (termasuk kenderaan interaktif merah dan kenderaan persekitaran hitam) mengikut trajektori yang sepadan dalam set data. Kenderaan sendiri yang dikawal oleh LFGC membuat keputusan yang serupa dengan pemandu manusia (kotak kelabu): kedua-dua LFGC dan pemandu manusia mula-mula cuba memecut dan bergabung di hadapan trak (kenderaan 1). Bagaimanapun, apabila menyedari bahawa trak itu lebih cenderung untuk terus mengalah, kenderaan sendiri memutuskan untuk memperlahankan dan bergabung di belakang trak.
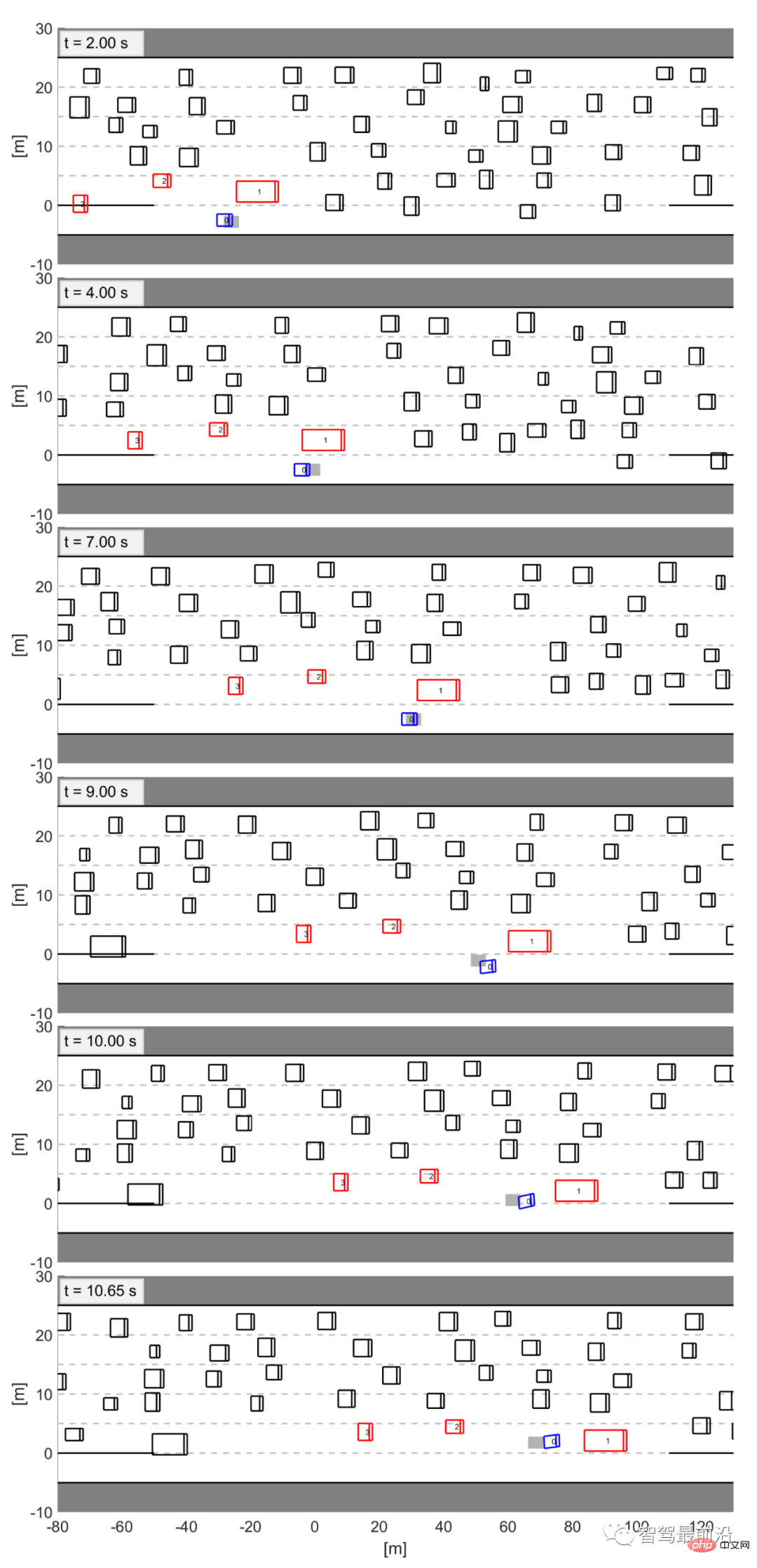
Rajah 12 Ilustrasi gabungan yang berjaya apabila mengesahkan LFGC pada set data Lebuhraya AS 101
Kenderaan biru ialah kenderaan sendiri yang dikawal oleh LFGC, dan kotak kelabu ialah lokasi kenderaan sendiri yang muncul dalam data.
06 Kesimpulan
Dalam kertas kerja ini, kami mencadangkan kaedah untuk perancangan dan kawalan kenderaan autonomi dalam senario gabungan (LFGC). LFGC mengambil ketidakpastian interaksi yang disebabkan oleh niat pemandu yang berbeza sebagai pembolehubah terpendam, menganggarkan niat pemandu lain dan memilih tindakan untuk menggalakkan penggabungan kenderaan sendiri. Khususnya, LFGC dapat melaksanakan sifat keselamatan kebarangkalian yang jelas, iaitu, tertakluk kepada kekangan keselamatan kenderaan.
Dengan mempertimbangkan interaksi berpasangan antara kenderaan sendiri dan kenderaan berinteraksi, LFGC dapat mengendalikan interaksi dengan berbilang kenderaan dengan cara yang boleh dikira. Akhir sekali, berbilang pengesahan berasaskan simulasi dijalankan untuk menunjukkan keberkesanan LFGC, termasuk senario di mana kereta lain mengikut ketua atau pengikut dalam permainan, model pemandu pintar (IDM) dan data Lebuhraya AS 101 yang sebenar.
Artikel ini diterjemahkan daripada "Ramalan Trajektori Sedar Interaksi dan Perancangan untuk Kenderaan Autonomi dalam Gabungan Paksa" Senario》
Atas ialah kandungan terperinci Ramalan trajektori dan perancangan untuk pemanduan autonomi di bawah penggabungan paksa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
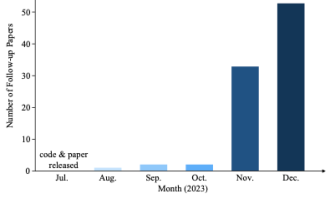 Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Ditulis di atas & pemahaman peribadi pengarang Gaussiansplatting tiga dimensi (3DGS) ialah teknologi transformatif yang telah muncul dalam bidang medan sinaran eksplisit dan grafik komputer dalam beberapa tahun kebelakangan ini. Kaedah inovatif ini dicirikan oleh penggunaan berjuta-juta Gaussians 3D, yang sangat berbeza daripada kaedah medan sinaran saraf (NeRF), yang terutamanya menggunakan model berasaskan koordinat tersirat untuk memetakan koordinat spatial kepada nilai piksel. Dengan perwakilan adegan yang eksplisit dan algoritma pemaparan yang boleh dibezakan, 3DGS bukan sahaja menjamin keupayaan pemaparan masa nyata, tetapi juga memperkenalkan tahap kawalan dan pengeditan adegan yang tidak pernah berlaku sebelum ini. Ini meletakkan 3DGS sebagai penukar permainan yang berpotensi untuk pembinaan semula dan perwakilan 3D generasi akan datang. Untuk tujuan ini, kami menyediakan gambaran keseluruhan sistematik tentang perkembangan dan kebimbangan terkini dalam bidang 3DGS buat kali pertama.
 Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Semalam semasa temu bual, saya telah ditanya sama ada saya telah membuat sebarang soalan berkaitan ekor panjang, jadi saya fikir saya akan memberikan ringkasan ringkas. Masalah ekor panjang pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi, iaitu, kemungkinan senario dengan kebarangkalian yang rendah untuk berlaku. Masalah ekor panjang yang dirasakan adalah salah satu sebab utama yang kini mengehadkan domain reka bentuk pengendalian kenderaan autonomi pintar satu kenderaan. Seni bina asas dan kebanyakan isu teknikal pemanduan autonomi telah diselesaikan, dan baki 5% masalah ekor panjang secara beransur-ansur menjadi kunci untuk menyekat pembangunan pemanduan autonomi. Masalah ini termasuk pelbagai senario yang berpecah-belah, situasi yang melampau dan tingkah laku manusia yang tidak dapat diramalkan. "Ekor panjang" senario tepi dalam pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi (AVs) kes Edge adalah senario yang mungkin dengan kebarangkalian yang rendah untuk berlaku. kejadian yang jarang berlaku ini
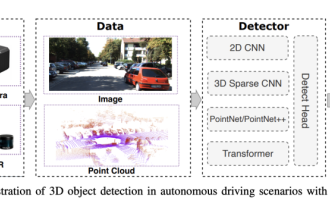 Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
0. Ditulis di hadapan&& Pemahaman peribadi bahawa sistem pemanduan autonomi bergantung pada persepsi lanjutan, membuat keputusan dan teknologi kawalan, dengan menggunakan pelbagai penderia (seperti kamera, lidar, radar, dll.) untuk melihat persekitaran sekeliling dan menggunakan algoritma dan model untuk analisis masa nyata dan membuat keputusan. Ini membolehkan kenderaan mengenali papan tanda jalan, mengesan dan menjejaki kenderaan lain, meramalkan tingkah laku pejalan kaki, dsb., dengan itu selamat beroperasi dan menyesuaikan diri dengan persekitaran trafik yang kompleks. Teknologi ini kini menarik perhatian meluas dan dianggap sebagai kawasan pembangunan penting dalam pengangkutan masa depan satu. Tetapi apa yang menyukarkan pemanduan autonomi ialah memikirkan cara membuat kereta itu memahami perkara yang berlaku di sekelilingnya. Ini memerlukan algoritma pengesanan objek tiga dimensi dalam sistem pemanduan autonomi boleh melihat dan menerangkan dengan tepat objek dalam persekitaran sekeliling, termasuk lokasinya,
 Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Ramalan trajektori memainkan peranan penting dalam pemanduan autonomi Ramalan trajektori pemanduan autonomi merujuk kepada meramalkan trajektori pemanduan masa hadapan kenderaan dengan menganalisis pelbagai data semasa proses pemanduan kenderaan. Sebagai modul teras pemanduan autonomi, kualiti ramalan trajektori adalah penting untuk kawalan perancangan hiliran. Tugas ramalan trajektori mempunyai timbunan teknologi yang kaya dan memerlukan kebiasaan dengan persepsi dinamik/statik pemanduan autonomi, peta ketepatan tinggi, garisan lorong, kemahiran seni bina rangkaian saraf (CNN&GNN&Transformer), dll. Sangat sukar untuk bermula! Ramai peminat berharap untuk memulakan ramalan trajektori secepat mungkin dan mengelakkan perangkap Hari ini saya akan mengambil kira beberapa masalah biasa dan kaedah pembelajaran pengenalan untuk ramalan trajektori! Pengetahuan berkaitan pengenalan 1. Adakah kertas pratonton teratur? A: Tengok survey dulu, hlm
 Adakah anda benar-benar menguasai penukaran sistem koordinat? Isu berbilang sensor yang tidak dapat dipisahkan daripada pemanduan autonomi
Oct 12, 2023 am 11:21 AM
Adakah anda benar-benar menguasai penukaran sistem koordinat? Isu berbilang sensor yang tidak dapat dipisahkan daripada pemanduan autonomi
Oct 12, 2023 am 11:21 AM
Artikel perintis dan utama pertama terutamanya memperkenalkan beberapa sistem koordinat yang biasa digunakan dalam teknologi pemanduan autonomi, dan cara melengkapkan korelasi dan penukaran antara mereka, dan akhirnya membina model persekitaran bersatu. Fokus di sini adalah untuk memahami penukaran daripada kenderaan kepada badan tegar kamera (parameter luaran), penukaran kamera kepada imej (parameter dalaman) dan penukaran unit imej kepada piksel. Penukaran daripada 3D kepada 2D akan mempunyai herotan, terjemahan, dsb. Perkara utama: Sistem koordinat kenderaan dan sistem koordinat badan kamera perlu ditulis semula: sistem koordinat satah dan sistem koordinat piksel Kesukaran: herotan imej mesti dipertimbangkan Kedua-dua penyahherotan dan penambahan herotan diberi pampasan pada satah imej. 2. Pengenalan Terdapat empat sistem penglihatan secara keseluruhannya: sistem koordinat satah piksel (u, v), sistem koordinat imej (x, y), sistem koordinat kamera () dan sistem koordinat dunia (). Terdapat hubungan antara setiap sistem koordinat,
 SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
Tajuk asal: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper pautan: https://arxiv.org/pdf/2402.02519.pdf Pautan kod: https://github.com/HKUST-Aerial-Robotics/SIMPL Unit pengarang: Universiti Sains Hong Kong dan Teknologi Idea Kertas DJI: Kertas kerja ini mencadangkan garis dasar ramalan pergerakan (SIMPL) yang mudah dan cekap untuk kenderaan autonomi. Berbanding dengan agen-sen tradisional
 SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
Ditulis di hadapan & titik permulaan Paradigma hujung ke hujung menggunakan rangka kerja bersatu untuk mencapai pelbagai tugas dalam sistem pemanduan autonomi. Walaupun kesederhanaan dan kejelasan paradigma ini, prestasi kaedah pemanduan autonomi hujung ke hujung pada subtugas masih jauh ketinggalan berbanding kaedah tugasan tunggal. Pada masa yang sama, ciri pandangan mata burung (BEV) padat yang digunakan secara meluas dalam kaedah hujung ke hujung sebelum ini menyukarkan untuk membuat skala kepada lebih banyak modaliti atau tugasan. Paradigma pemanduan autonomi hujung ke hujung (SparseAD) tertumpu carian jarang dicadangkan di sini, di mana carian jarang mewakili sepenuhnya keseluruhan senario pemanduan, termasuk ruang, masa dan tugas, tanpa sebarang perwakilan BEV yang padat. Khususnya, seni bina jarang bersatu direka bentuk untuk kesedaran tugas termasuk pengesanan, penjejakan dan pemetaan dalam talian. Di samping itu, berat
 Mari kita bincangkan tentang sistem pemanduan autonomi hujung ke hujung dan generasi seterusnya, serta beberapa salah faham tentang pemanduan autonomi hujung ke hujung?
Apr 15, 2024 pm 04:13 PM
Mari kita bincangkan tentang sistem pemanduan autonomi hujung ke hujung dan generasi seterusnya, serta beberapa salah faham tentang pemanduan autonomi hujung ke hujung?
Apr 15, 2024 pm 04:13 PM
Pada bulan lalu, atas sebab-sebab yang diketahui umum, saya telah mengadakan pertukaran yang sangat intensif dengan pelbagai guru dan rakan sekelas dalam industri. Topik yang tidak dapat dielakkan dalam pertukaran secara semula jadi adalah hujung ke hujung dan Tesla FSDV12 yang popular. Saya ingin mengambil kesempatan ini untuk menyelesaikan beberapa buah fikiran dan pendapat saya pada masa ini untuk rujukan dan perbincangan anda. Bagaimana untuk mentakrifkan sistem pemanduan autonomi hujung ke hujung, dan apakah masalah yang sepatutnya dijangka diselesaikan hujung ke hujung? Menurut definisi yang paling tradisional, sistem hujung ke hujung merujuk kepada sistem yang memasukkan maklumat mentah daripada penderia dan secara langsung mengeluarkan pembolehubah yang membimbangkan tugas. Sebagai contoh, dalam pengecaman imej, CNN boleh dipanggil hujung-ke-hujung berbanding kaedah pengekstrak ciri + pengelas tradisional. Dalam tugas pemanduan autonomi, masukkan data daripada pelbagai penderia (kamera/LiDAR





