 Peranti teknologi
Peranti teknologi
 AI
AI
 18 gambar untuk memahami rangkaian saraf, manifold dan topologi secara intuitif
18 gambar untuk memahami rangkaian saraf, manifold dan topologi secara intuitif
18 gambar untuk memahami rangkaian saraf, manifold dan topologi secara intuitif
Setakat ini, salah satu kebimbangan besar mengenai rangkaian saraf ialah ia adalah kotak hitam yang sukar untuk dijelaskan. Artikel ini secara teorinya memahami sebab rangkaian saraf sangat berkesan dalam pengecaman dan pengelasan corak Intipatinya adalah untuk memesongkan dan mengubah bentuk input asal melalui lapisan transformasi afin dan transformasi tak linear sehingga ia boleh dibezakan dengan mudah ke dalam kategori yang berbeza. Malah, algoritma perambatan belakang (BP) sebenarnya secara berterusan memperhalusi kesan herotan berdasarkan data latihan.
Bermula kira-kira sepuluh tahun yang lalu, rangkaian saraf dalam telah mencapai keputusan terobosan dalam bidang seperti penglihatan komputer, membangkitkan minat dan perhatian yang besar.
Namun, sebilangan orang masih bimbang. Satu sebab ialah rangkaian saraf ialah kotak hitam: jika rangkaian saraf dilatih dengan baik, hasil berkualiti tinggi boleh diperolehi, tetapi sukar untuk memahami cara ia berfungsi. Jika rangkaian saraf tidak berfungsi, sukar untuk menentukan masalahnya.
Walaupun sukar untuk memahami rangkaian saraf dalam secara keseluruhan, anda boleh bermula dengan rangkaian saraf dalam berdimensi rendah, iaitu rangkaian dengan hanya beberapa neuron dalam setiap lapisan, yang lebih mudah difahami. Kita boleh memahami tingkah laku dan latihan rangkaian saraf dalam dimensi rendah melalui kaedah visualisasi. Kaedah visualisasi membolehkan kita memahami kelakuan rangkaian saraf dengan lebih intuitif dan memerhatikan hubungan antara rangkaian saraf dan topologi.
Seterusnya saya akan bercakap tentang banyak perkara menarik, termasuk batas bawah pada kerumitan rangkaian saraf yang mampu mengklasifikasikan set data tertentu.
1. Contoh mudah
Mari kita mulakan dengan set data yang sangat mudah. Dalam rajah di bawah, dua lengkung pada satah terdiri daripada titik yang tidak terkira banyaknya. Rangkaian saraf akan cuba membezakan garis mana yang dimiliki oleh titik-titik ini.
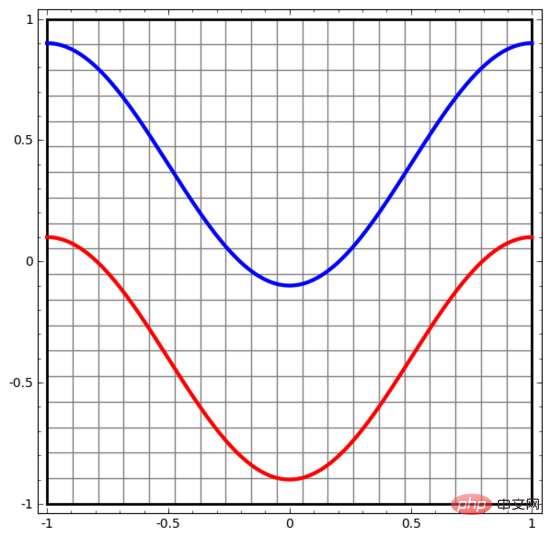
Cara paling mudah untuk memerhati kelakuan rangkaian saraf (atau mana-mana algoritma pengelasan) ialah melihat cara ia mengelaskan setiap titik data.
Kami bermula dengan rangkaian saraf paling ringkas, yang hanya mempunyai satu lapisan input dan satu lapisan output. Rangkaian saraf sedemikian hanya memisahkan dua jenis titik data dengan garis lurus.
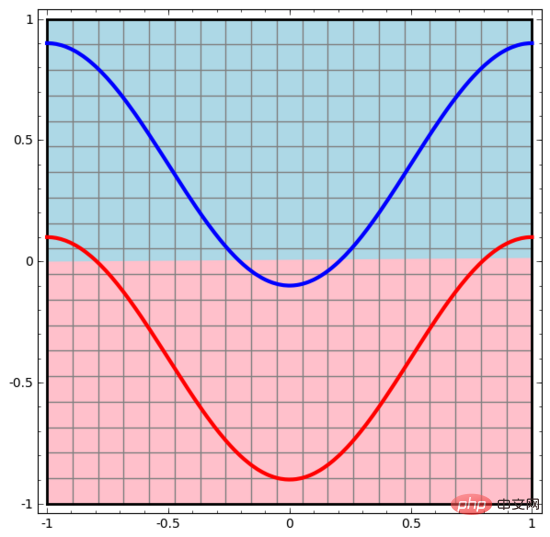
Rangkaian saraf sedemikian terlalu mudah dan kasar. Rangkaian saraf moden selalunya mempunyai berbilang lapisan antara lapisan input dan output, dipanggil lapisan tersembunyi. Malah rangkaian saraf moden yang paling ringkas mempunyai sekurang-kurangnya satu lapisan tersembunyi.
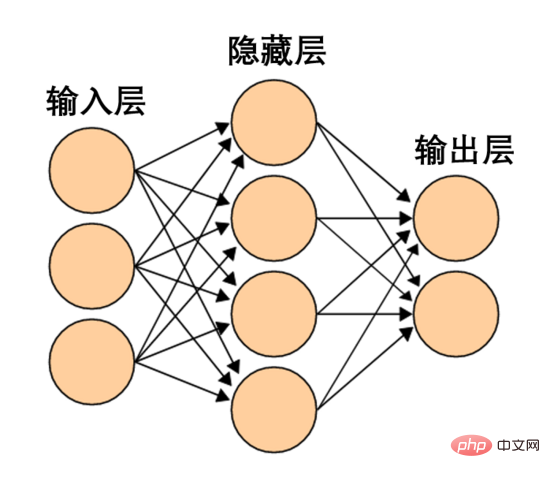
Rangkaian saraf ringkas, sumber Wikipedia
Begitu juga, kami memerhatikan apa yang dilakukan oleh rangkaian saraf untuk setiap titik data. Seperti yang dapat dilihat, rangkaian saraf ini menggunakan lengkung dan bukannya garis lurus untuk memisahkan titik data. Jelas sekali, lengkung lebih kompleks daripada garis lurus.
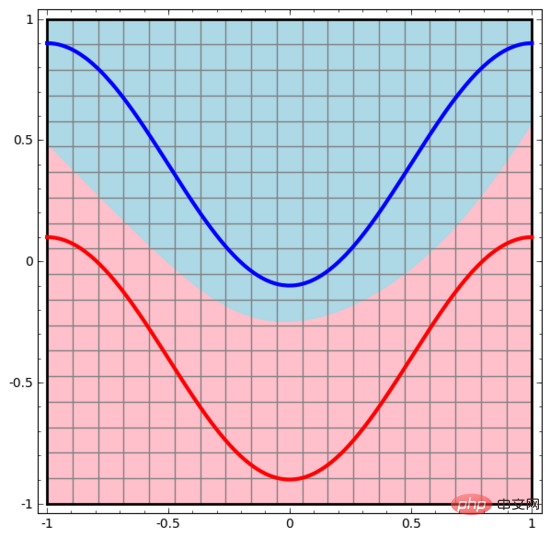
Setiap lapisan rangkaian saraf menggunakan perwakilan baharu untuk mewakili data. Kita boleh melihat bagaimana data diubah menjadi perwakilan baharu dan bagaimana rangkaian saraf mengklasifikasikannya. Dalam lapisan perwakilan terakhir, rangkaian saraf melukis garis antara dua jenis data (atau satah hiper jika dalam dimensi yang lebih tinggi).
Dalam visualisasi sebelumnya, kami melihat perwakilan mentah data. Anda boleh menganggapnya sebagai rupa data dalam "lapisan input". Sekarang mari kita lihat rupa data selepas ia diubah Anda boleh menganggapnya sebagai rupa data dalam "lapisan tersembunyi".
Setiap dimensi data sepadan dengan pengaktifan neuron dalam lapisan rangkaian saraf.
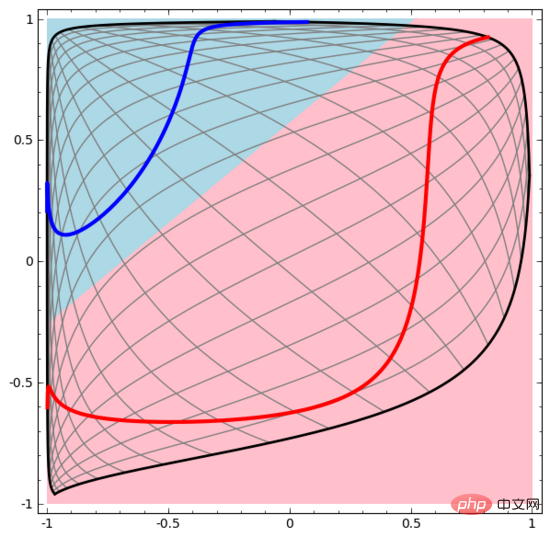
Lapisan tersembunyi menggunakan kaedah di atas untuk mewakili data, supaya data boleh dipisahkan dengan garis lurus (iaitu, boleh dipisahkan secara linear)
2. Visualisasi lapisan berterusan
Dalam kaedah dalam bahagian sebelumnya, setiap lapisan rangkaian saraf menggunakan perwakilan yang berbeza untuk mewakili data. Dengan cara ini, perwakilan setiap lapisan adalah diskret dan tidak berterusan.
Ini menimbulkan kesukaran dalam pemahaman kita Bagaimana untuk menukar daripada satu perwakilan kepada yang lain? Nasib baik, ciri-ciri lapisan rangkaian saraf menjadikannya sangat mudah untuk memahami aspek ini.
Terdapat pelbagai lapisan berbeza dalam rangkaian saraf. Di bawah ini kita akan membincangkan lapisan tanh sebagai contoh khusus. Lapisan tanh, termasuk:
- Gunakan matriks "berat" W untuk transformasi linear
- Gunakan vektor b untuk terjemahan
- Gunakan tanh untuk mewakili titik demi titik
Kita boleh menganggapnya sebagai transformasi berterusan seperti berikut:
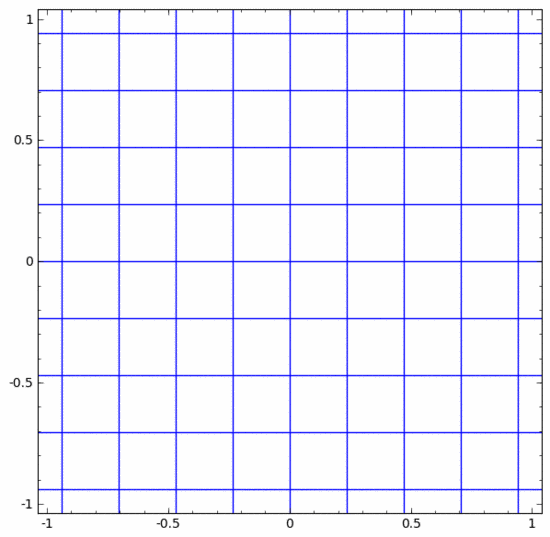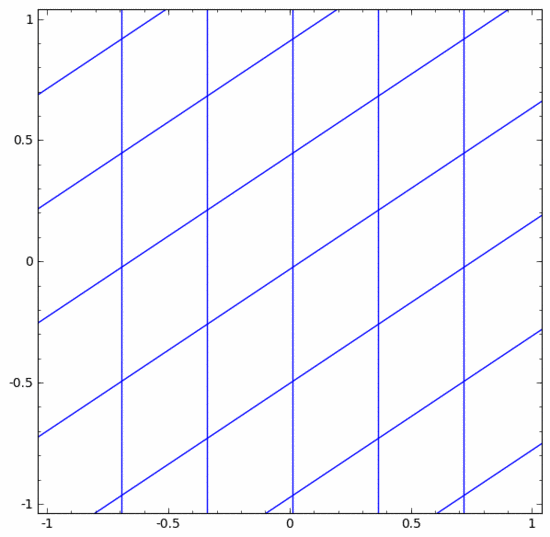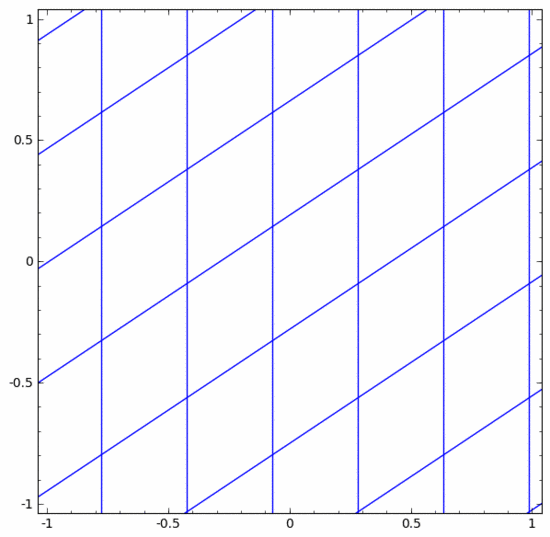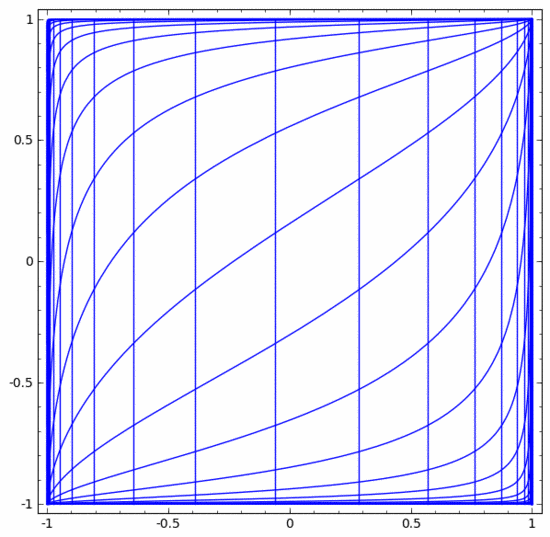
Lapisan piawai lain adalah sama, terdiri daripada aplikasi transformasi affine dan fungsi pengaktifan monotonik.
Kita boleh menggunakan kaedah ini untuk memahami rangkaian saraf yang lebih kompleks. Sebagai contoh, rangkaian saraf di bawah menggunakan empat lapisan tersembunyi untuk mengklasifikasikan dua lingkaran yang sedikit berjalin. Dapat dilihat bahawa untuk mengklasifikasikan data, perwakilan data diubah secara berterusan. Kedua-dua lingkaran pada mulanya terikat, tetapi akhirnya ia boleh dipisahkan oleh garis lurus (boleh dipisahkan secara linear).
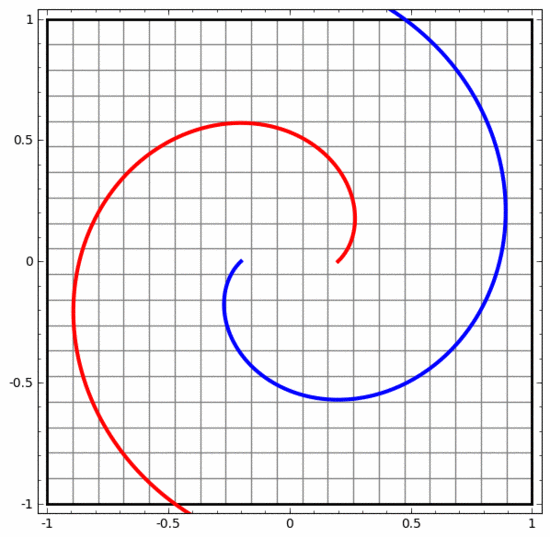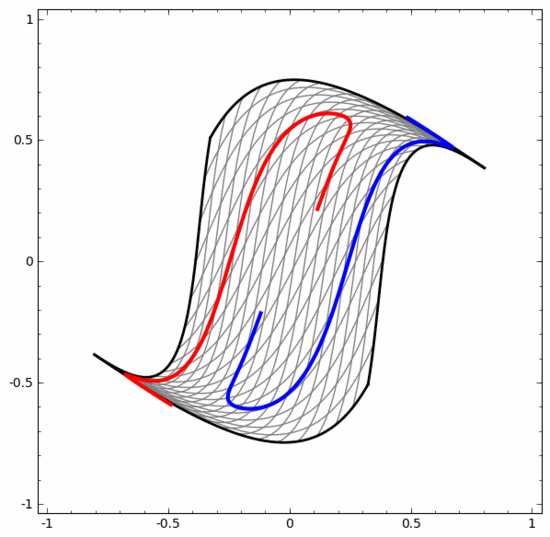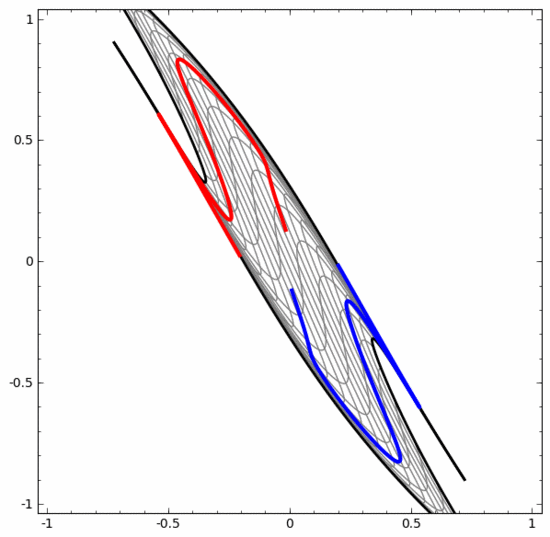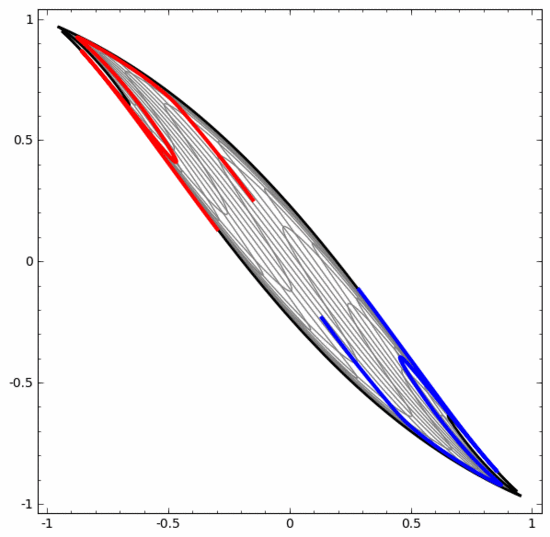
Sebaliknya, walaupun rangkaian saraf di bawah juga menggunakan berbilang lapisan tersembunyi, ia tidak boleh membahagikan dua lagi lingkaran yang saling berjalin.
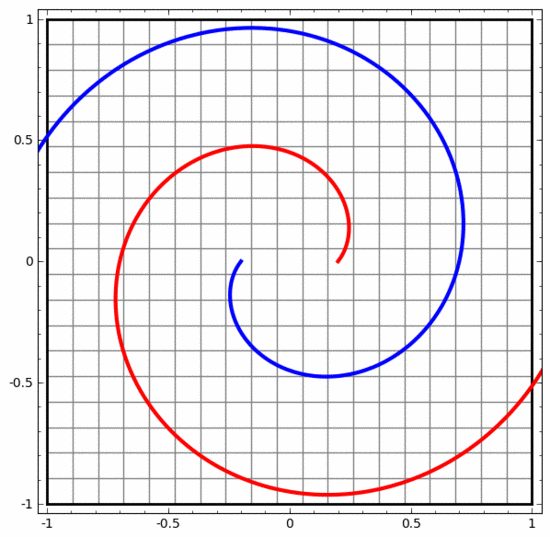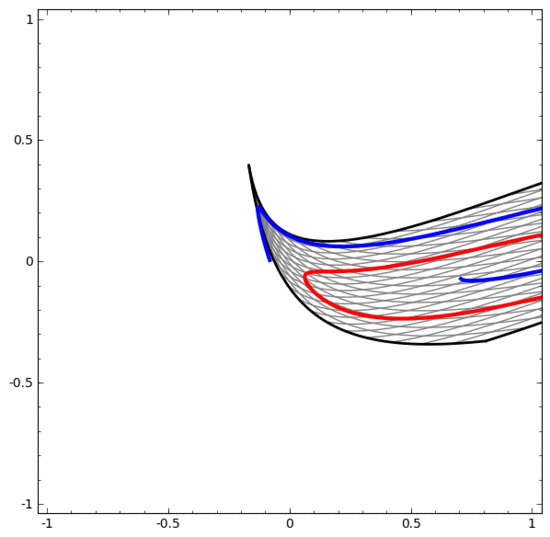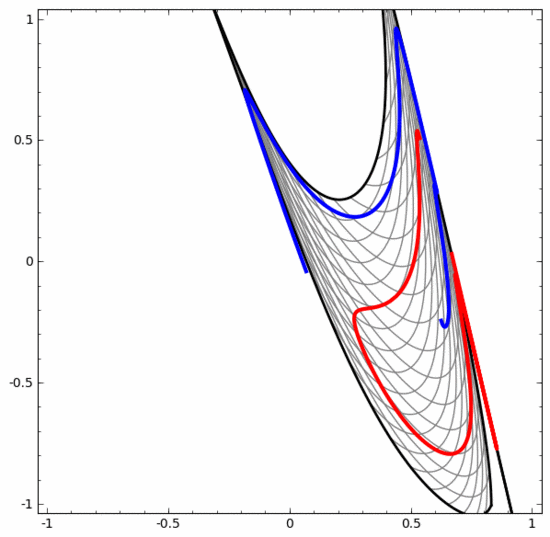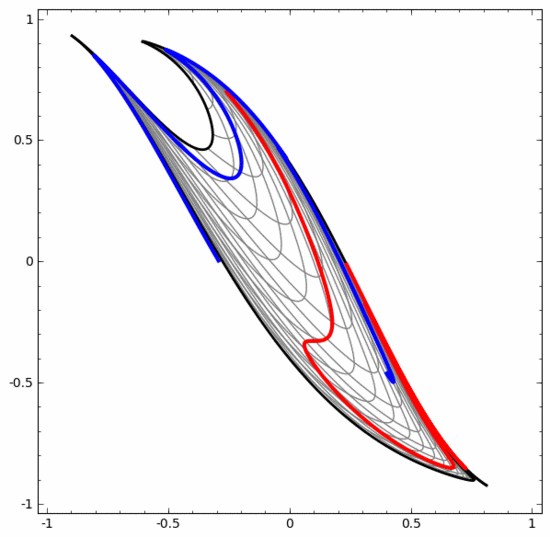
Perlu dinyatakan dengan jelas bahawa dua tugas klasifikasi lingkaran di atas mempunyai beberapa cabaran kerana kami pada masa ini hanya menggunakan rangkaian saraf dimensi rendah. Segala-galanya akan menjadi lebih mudah jika kita menggunakan rangkaian saraf yang lebih luas.
(Andrej Karpathy membuat demo yang baik berdasarkan ConvnetJS, yang membolehkan orang ramai meneroka rangkaian saraf secara interaktif melalui latihan visual seperti ini.)
3 Topologi lapisan tanh
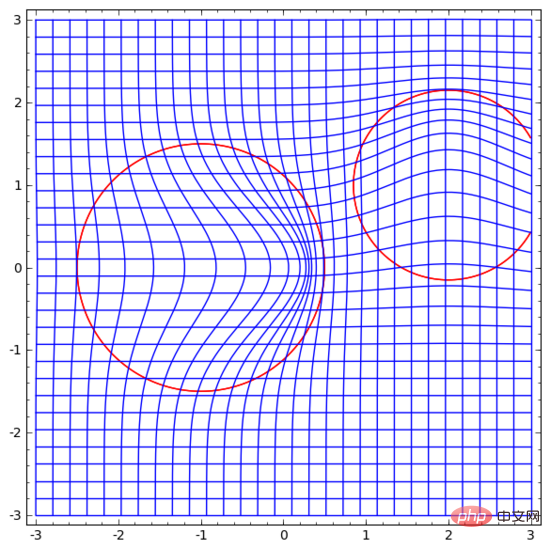
Setiap lapisan rangkaian saraf meregang dan memerah ruang, tetapi ia tidak menggunting, membelah atau melipat ruang. Secara intuitif, rangkaian saraf tidak memusnahkan sifat topologi data. Sebagai contoh, jika satu set data adalah berterusan, maka perwakilan berubahnya juga akan berterusan (dan sebaliknya).
Transformasi seperti ini yang tidak menjejaskan sifat topologi dipanggil homeomorphisms. Secara formal, ia adalah bijeksi bagi fungsi berterusan dua arah.
Teorem: Jika matriks berat W adalah bukan tunggal, dan lapisan rangkaian saraf mempunyai N input dan N output, maka pemetaan lapisan ini adalah homeomorphic (untuk domain tertentu dan julat nilai).
Bukti: Mari kita pergi langkah demi langkah:
1. Anggapkan bahawa W mempunyai penentu bukan sifar. Kemudian ia adalah fungsi linear bilinear dengan songsang linear. Fungsi linear adalah berterusan. Kemudian transformasi seperti "darab dengan W" ialah homeomorphisme; ialah fungsi selanjar dengan songsangan selanjar. (untuk domain dan julat tertentu), ia adalah bijection, dan aplikasi dari segi titiknya ialah homeomorphism.
Oleh itu, jika W mempunyai penentu bukan sifar, lapisan rangkaian neural ini adalah homeomorfik.
Hasil ini masih berlaku jika kita menggabungkan lapisan sedemikian secara rawak.
4. Topologi dan klasifikasi
Mari kita lihat set data dua dimensi, yang mengandungi dua jenis data A dan B:

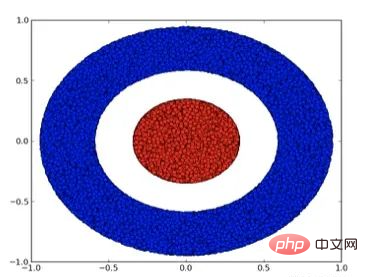 Nota: Untuk mengklasifikasikan set data ini, rangkaian saraf (tanpa mengira kedalaman) mesti mempunyai unit tersembunyi dengan 3 atau lebih lapisan .
Nota: Untuk mengklasifikasikan set data ini, rangkaian saraf (tanpa mengira kedalaman) mesti mempunyai unit tersembunyi dengan 3 atau lebih lapisan .
Seperti yang dinyatakan di atas, menggunakan unit sigmoid atau lapisan softmax untuk pengelasan adalah bersamaan dengan mencari satah hiper (dalam kes ini, garis lurus) dalam perwakilan lapisan terakhir untuk memisahkan A dan B. Dengan hanya dua unit tersembunyi, rangkaian saraf secara topologi tidak dapat memisahkan data dengan cara ini dan dengan itu tidak dapat mengklasifikasikan set data di atas.
Dalam visualisasi di bawah, lapisan tersembunyi mengubah perwakilan data, dengan garis lurus sebagai garis pemisah. Ia boleh dilihat bahawa garis pemisah terus berputar dan bergerak, tetapi ia tidak pernah dapat memisahkan dua jenis data A dan B dengan baik.
Tidak kira betapa terlatihnya rangkaian saraf, ia tidak dapat menyelesaikan tugas pengelasan dengan baik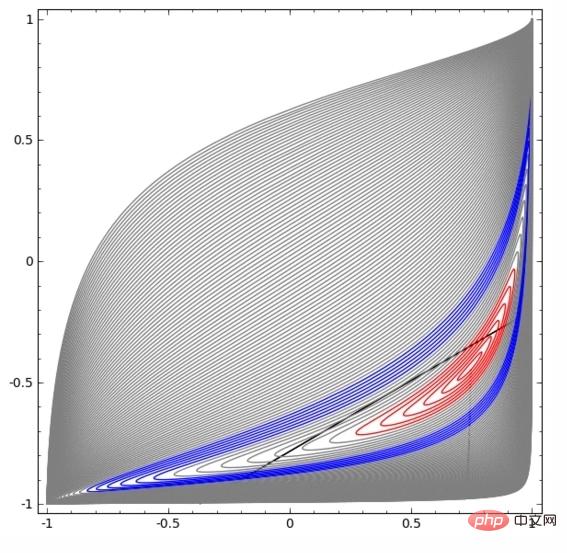 Akhirnya, ia hanya dapat mencapai minimum tempatan , mencapai ketepatan klasifikasi 80%.
Akhirnya, ia hanya dapat mencapai minimum tempatan , mencapai ketepatan klasifikasi 80%.
Contoh di atas hanya mempunyai satu lapisan tersembunyi, dan kerana hanya terdapat dua unit tersembunyi, ia akan gagal dalam pengelasan.
Bukti: Jika terdapat hanya dua unit tersembunyi, sama ada transformasi lapisan ini adalah homeomorfik, atau matriks berat lapisan mempunyai penentu 0. Jika ia adalah homeomorphism, A masih dikelilingi oleh B, dan A dan B tidak boleh dipisahkan oleh garis lurus. Jika terdapat penentu 0, maka set data akan runtuh pada beberapa paksi. Oleh kerana A dikelilingi oleh B, lipatan A pada mana-mana paksi akan menyebabkan beberapa titik data A bercampur dengan B, menjadikannya mustahil untuk membezakan A daripada B.
Tetapi jika kita menambah unit tersembunyi ketiga, masalahnya selesai. Pada masa ini, rangkaian saraf boleh menukar data kepada perwakilan berikut:
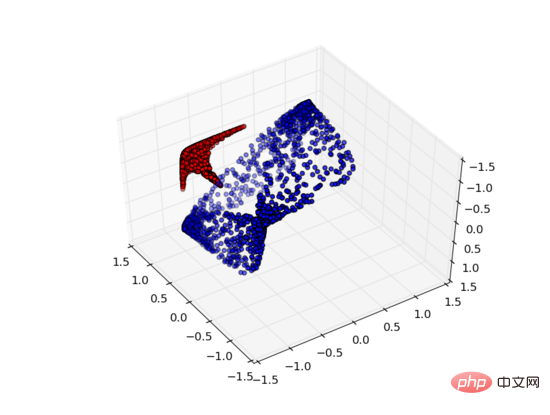
Pada masa ini, hyperplane boleh digunakan untuk memisahkan A dan B.
Untuk menjelaskan prinsipnya dengan lebih baik, berikut ialah set data satu dimensi yang lebih mudah sebagai contoh:
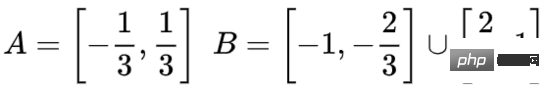
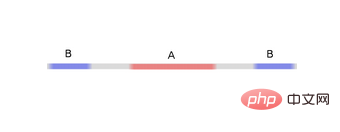
Untuk mengklasifikasikan set data ini, lapisan yang terdiri daripada dua atau lebih unit tersembunyi mesti digunakan. Jika anda menggunakan dua unit tersembunyi, anda boleh mewakili data dengan lengkung yang bagus, supaya A dan B boleh dipisahkan dengan garis lurus:
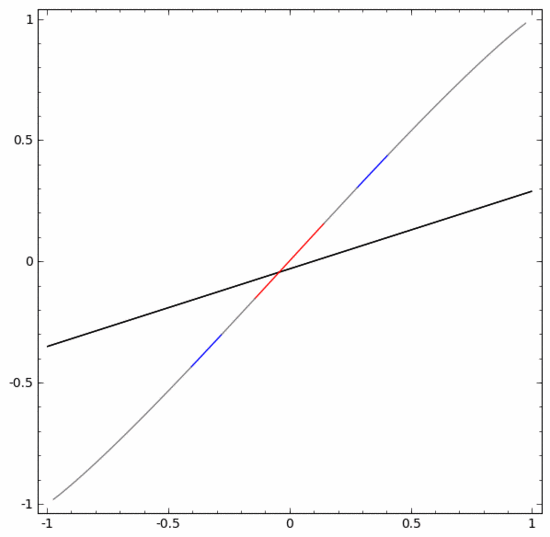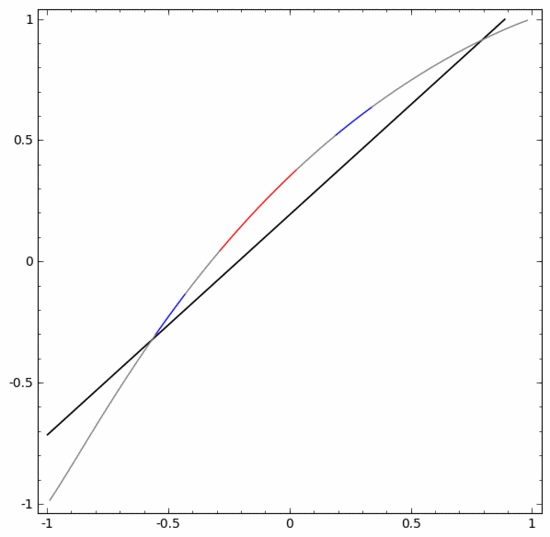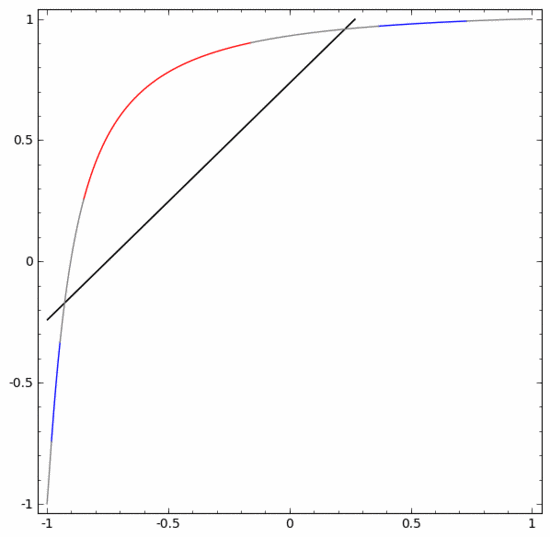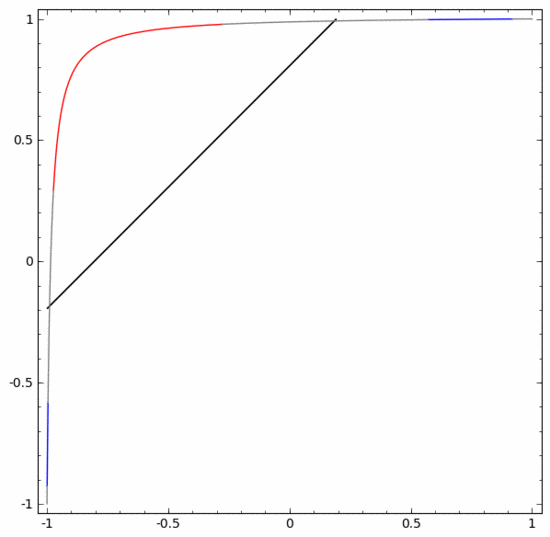
Bagaimana untuk melakukannya Apa tentang? Apabila  , salah satu unit tersembunyi diaktifkan; apabila
, salah satu unit tersembunyi diaktifkan; apabila 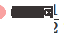 , unit tersembunyi yang lain diaktifkan. Apabila unit tersembunyi sebelumnya diaktifkan dan unit tersembunyi seterusnya tidak diaktifkan, ia boleh dinilai bahawa ini adalah titik data kepunyaan A.
, unit tersembunyi yang lain diaktifkan. Apabila unit tersembunyi sebelumnya diaktifkan dan unit tersembunyi seterusnya tidak diaktifkan, ia boleh dinilai bahawa ini adalah titik data kepunyaan A.
5. Hipotesis Manifold
Adakah hipotesis manifold bermakna untuk memproses set data dunia sebenar (seperti data imej)? Saya rasa ia masuk akal.
Hipotesis manifold bermaksud data semula jadi membentuk manifold berdimensi rendah dalam ruang benamnya. Hipotesis ini mempunyai sokongan teori dan eksperimen. Jika anda percaya pada hipotesis manifold, maka tugas algoritma klasifikasi bermuara kepada memisahkan satu set manifold terjerat.
Dalam contoh sebelumnya, satu kelas mengelilingi kelas yang lain sepenuhnya. Walau bagaimanapun, dalam data dunia sebenar, tidak mungkin manifold imej anjing akan dikelilingi sepenuhnya oleh manifold imej kucing. Walau bagaimanapun, situasi topologi lain yang lebih munasabah masih boleh menyebabkan masalah, seperti yang akan dibincangkan dalam bahagian seterusnya.
6. Pautan dan homotopi
Seterusnya saya akan bercakap tentang satu lagi set data yang menarik: dua torus (tori), A dan B.

Sama seperti situasi set data yang kita bincangkan sebelum ini, anda tidak boleh memisahkan set data n-dimensi tanpa menggunakan dimensi n+1 (dimensi n+1 digunakan di sini) Dalam kes ini ia adalah dimensi ke-4).
Masalah pautan tergolong dalam teori simpulan dalam topologi. Kadang-kadang, apabila kita melihat pautan, kita tidak dapat mengetahui dengan segera sama ada ia adalah pautan yang rosak (nyahpaut bermakna walaupun ia terikat antara satu sama lain, ia boleh dipisahkan melalui ubah bentuk berterusan).
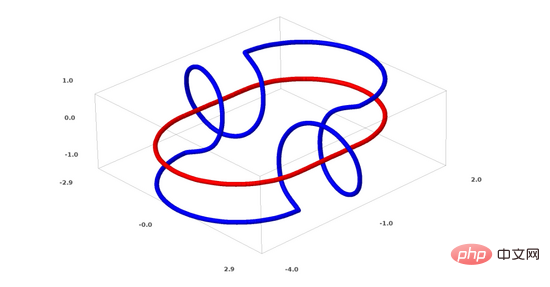
Pautan terputus yang lebih mudah
Jika rangkaian saraf dengan hanya 3 unit tersembunyi dalam lapisan tersembunyi boleh mengklasifikasikan set data, maka set data ini Ia adalah pautan rosak (soalannya: secara teorinya, bolehkah semua pautan rosak diklasifikasikan oleh rangkaian saraf dengan hanya 3 unit tersembunyi?).
Dari perspektif teori simpulan, visualisasi berterusan perwakilan data yang dihasilkan oleh rangkaian saraf bukan sekadar animasi yang bagus, tetapi juga proses membongkar pautan. Dalam topologi, kami memanggil ini isotopi ambien antara pautan asal dan pautan terpisah.
Homomorfisme sekeliling antara manifold A dan manifold B ialah fungsi berterusan:

Setiap satu ialah homeomorfisme X. ialah fungsi ciri, memetakan A ke B. Iaitu, sentiasa beralih daripada memetakan A kepada dirinya sendiri kepada memetakan A kepada B.
Teorem: Jika tiga syarat berikut dipenuhi pada masa yang sama: (1) W adalah bukan tunggal; (2) susunan neuron dalam lapisan tersembunyi boleh disusun secara manual; adalah lebih besar daripada 1, maka input rangkaian saraf Terdapat persamaan lilitan antara perwakilan yang dihasilkan oleh lapisan rangkaian saraf.
Bukti: Kami juga pergi langkah demi langkah:
1. Untuk mencapai penjelmaan linear, kita memerlukan W untuk mempunyai penentu positif. Premis kami ialah penentu bukan sifar, dan jika penentu negatif, kita boleh mengubahnya menjadi positif dengan menukar dua neuron tersembunyi. Ruang matriks penentu positif adalah bersambung laluan, jadi terdapat 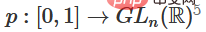 , oleh itu,
, oleh itu, 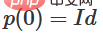 ,
, 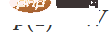 . Dengan fungsi 〈🎜〉, kita boleh teruskan mengalihkan fungsi eigen kepada penjelmaan W, mendarab x dengan matriks peralihan berterusan pada setiap titik pada masa t.
. Dengan fungsi 〈🎜〉, kita boleh teruskan mengalihkan fungsi eigen kepada penjelmaan W, mendarab x dengan matriks peralihan berterusan pada setiap titik pada masa t. 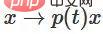
. 
boleh digunakan untuk beralih daripada fungsi ciri kepada aplikasi titik demi titik . 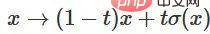
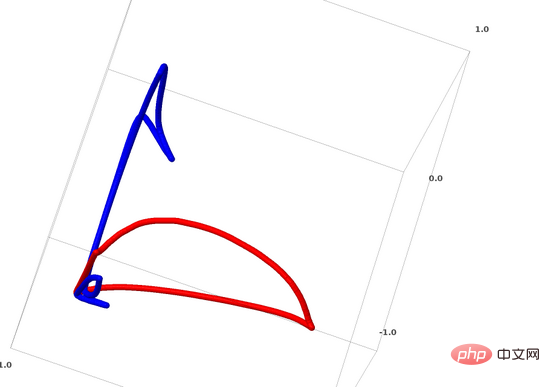
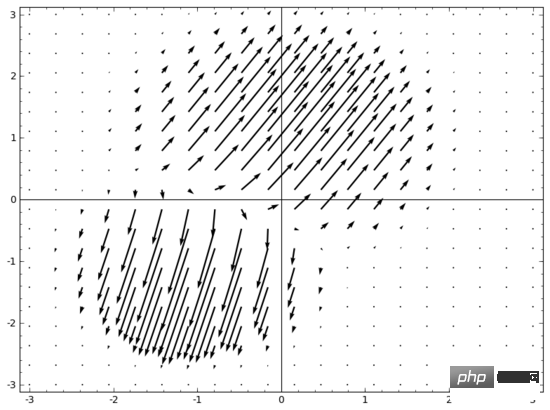
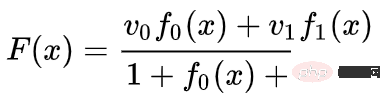
di mana dan ialah vektor, dan merupakan fungsi Gaussian n-dimensi. Idea ini diilhamkan oleh fungsi asas jejari.
9. Lapisan jiran terdekat K
Perkara saya yang lain ialah kebolehpisahan linear mungkin merupakan keperluan yang berlebihan dan tidak munasabah untuk rangkaian saraf, mungkin menggunakan jiran terdekat k (k-NN) akan menjadi lebih baik. Walau bagaimanapun, algoritma k-NN banyak bergantung kepada perwakilan data Oleh itu, perwakilan data yang baik diperlukan untuk algoritma k-NN untuk mencapai keputusan yang baik.
Dalam percubaan pertama, saya melatih beberapa rangkaian saraf MNIST (CNN dua lapisan, tiada keciciran) dengan kadar ralat di bawah 1%. Kemudian, saya membuang lapisan softmax terakhir dan menggunakan algoritma k-NN, dan beberapa kali keputusan menunjukkan bahawa kadar ralat dikurangkan sebanyak 0.1-0.2%.
Namun, saya rasa pendekatan ini masih salah. Rangkaian saraf masih cuba mengklasifikasikan secara linear, tetapi disebabkan penggunaan algoritma k-NN, ia boleh membetulkan sedikit beberapa ralat yang dibuatnya, dengan itu mengurangkan kadar ralat.
Disebabkan pemberat (1/jarak), k-NN boleh dibezakan dengan perwakilan data yang ia bertindak. Oleh itu, kita boleh terus melatih rangkaian saraf untuk klasifikasi k-NN. Ini boleh dianggap sebagai lapisan "jiran terdekat", yang bertindak serupa dengan lapisan softmax.
Kami tidak mahu memberi maklum balas kepada keseluruhan set latihan untuk setiap kumpulan mini kerana ia terlalu mahal dari segi pengiraan. Saya fikir pendekatan yang baik adalah untuk mengklasifikasikan setiap elemen dalam kelompok mini berdasarkan kategori elemen lain dalam kelompok mini, memberikan setiap elemen berat (1/(jarak dari sasaran pengelasan)).
Malangnya, walaupun dengan seni bina yang kompleks, menggunakan algoritma k-NN hanya boleh mengurangkan kadar ralat kepada 4-5%, manakala menggunakan seni bina mudah kadar ralat adalah lebih tinggi. Walau bagaimanapun, saya tidak banyak berusaha ke dalam hiperparameter.
Tetapi saya masih suka algoritma k-NN kerana ia lebih sesuai untuk rangkaian saraf. Kami mahu mata pada manifold yang sama lebih dekat antara satu sama lain, dan bukannya mendesak menggunakan hyperplanes untuk memisahkan manifold. Ini sama dengan mengecutkan satu manifold sambil menjadikan ruang antara manifold kategori berbeza lebih besar. Ini memudahkan masalah.
10. Ringkasan
Sesetengah ciri topologi data mungkin menyebabkan data ini tidak dapat dipisahkan secara linear menggunakan rangkaian saraf berdimensi rendah (tanpa mengira kedalaman rangkaian saraf). Walaupun secara teknikalnya mungkin, seperti lingkaran, pemisahan sangat sukar dicapai dengan rangkaian saraf berdimensi rendah.
Untuk mengklasifikasikan data dengan tepat, rangkaian saraf kadangkala memerlukan lapisan yang lebih luas. Di samping itu, lapisan rangkaian neural tradisional tidak sesuai untuk memanipulasi manifold walaupun pemberat ditetapkan secara manual, sukar untuk mendapatkan perwakilan transformasi data yang ideal. Lapisan rangkaian saraf baharu mungkin boleh memainkan peranan sokongan yang baik, terutamanya lapisan rangkaian saraf baharu yang diilhamkan dengan memahami pembelajaran mesin daripada perspektif pelbagai.
Atas ialah kandungan terperinci 18 gambar untuk memahami rangkaian saraf, manifold dan topologi secara intuitif. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
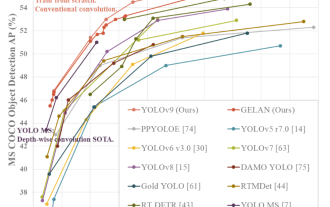 YOLO adalah abadi! YOLOv9 dikeluarkan: prestasi dan kelajuan SOTA~
Feb 26, 2024 am 11:31 AM
YOLO adalah abadi! YOLOv9 dikeluarkan: prestasi dan kelajuan SOTA~
Feb 26, 2024 am 11:31 AM
Kaedah pembelajaran mendalam hari ini memberi tumpuan kepada mereka bentuk fungsi objektif yang paling sesuai supaya keputusan ramalan model paling hampir dengan situasi sebenar. Pada masa yang sama, seni bina yang sesuai mesti direka bentuk untuk mendapatkan maklumat yang mencukupi untuk ramalan. Kaedah sedia ada mengabaikan fakta bahawa apabila data input mengalami pengekstrakan ciri lapisan demi lapisan dan transformasi spatial, sejumlah besar maklumat akan hilang. Artikel ini akan menyelidiki isu penting apabila menghantar data melalui rangkaian dalam, iaitu kesesakan maklumat dan fungsi boleh balik. Berdasarkan ini, konsep maklumat kecerunan boleh atur cara (PGI) dicadangkan untuk menghadapi pelbagai perubahan yang diperlukan oleh rangkaian dalam untuk mencapai pelbagai objektif. PGI boleh menyediakan maklumat input lengkap untuk tugas sasaran untuk mengira fungsi objektif, dengan itu mendapatkan maklumat kecerunan yang boleh dipercayai untuk mengemas kini berat rangkaian. Di samping itu, rangka kerja rangkaian ringan baharu direka bentuk
 Asas, sempadan dan aplikasi GNN
Apr 11, 2023 pm 11:40 PM
Asas, sempadan dan aplikasi GNN
Apr 11, 2023 pm 11:40 PM
Rangkaian saraf graf (GNN) telah mencapai kemajuan yang pesat dan luar biasa dalam beberapa tahun kebelakangan ini. Rangkaian saraf graf, juga dikenali sebagai pembelajaran dalam graf, pembelajaran perwakilan graf (pembelajaran perwakilan graf) atau pembelajaran dalam geometri, ialah topik penyelidikan yang paling pesat berkembang dalam bidang pembelajaran mesin, terutamanya pembelajaran mendalam. Tajuk perkongsian ini ialah "Asas, Sempadan dan Aplikasi GNN", yang terutamanya memperkenalkan kandungan umum buku komprehensif "Asas, Sempadan dan Aplikasi Rangkaian Neural Graf" yang disusun oleh sarjana Wu Lingfei, Cui Peng, Pei Jian dan Zhao Liang. 1. Pengenalan kepada rangkaian neural graf 1. Mengapa mengkaji graf? Graf ialah bahasa universal untuk menerangkan dan memodelkan sistem yang kompleks. Graf itu sendiri tidak rumit, ia terutamanya terdiri daripada tepi dan nod. Kita boleh menggunakan nod untuk mewakili mana-mana objek yang ingin kita modelkan, dan tepi untuk mewakili dua
 Gambaran keseluruhan tiga seni bina cip arus perdana untuk pemanduan autonomi dalam satu artikel
Apr 12, 2023 pm 12:07 PM
Gambaran keseluruhan tiga seni bina cip arus perdana untuk pemanduan autonomi dalam satu artikel
Apr 12, 2023 pm 12:07 PM
Cip AI arus perdana semasa terutamanya dibahagikan kepada tiga kategori: GPU, FPGA dan ASIC. Kedua-dua GPU dan FPGA adalah seni bina cip yang agak matang pada peringkat awal dan merupakan cip kegunaan umum. ASIC ialah cip yang disesuaikan untuk senario AI tertentu. Industri telah mengesahkan bahawa CPU tidak sesuai untuk pengkomputeran AI, tetapi ia juga penting dalam aplikasi AI. Seni Bina Penyelesaian GPU Perbandingan antara GPU dan CPU CPU mengikut seni bina von Neumann, terasnya ialah penyimpanan atur cara/data dan pelaksanaan bersiri. Oleh itu, seni bina CPU memerlukan sejumlah besar ruang untuk meletakkan unit storan (Cache) dan unit kawalan (Control) Sebaliknya, unit pengkomputeran (ALU) hanya menduduki sebahagian kecil, jadi CPU berfungsi secara besar-besaran. pengkomputeran selari.
 'Pemilik Bilibili UP berjaya mencipta rangkaian neural berasaskan batu merah pertama di dunia, yang menyebabkan sensasi di media sosial dan dipuji oleh Yann LeCun.'
May 07, 2023 pm 10:58 PM
'Pemilik Bilibili UP berjaya mencipta rangkaian neural berasaskan batu merah pertama di dunia, yang menyebabkan sensasi di media sosial dan dipuji oleh Yann LeCun.'
May 07, 2023 pm 10:58 PM
Dalam Minecraft, batu merah adalah item yang sangat penting. Ia adalah bahan unik dalam permainan Suis, obor batu merah, dan blok batu merah boleh memberikan tenaga seperti elektrik kepada wayar atau objek. Litar Redstone boleh digunakan untuk membina struktur untuk anda mengawal atau mengaktifkan jentera lain Ia sendiri boleh direka bentuk untuk bertindak balas kepada pengaktifan manual oleh pemain, atau mereka boleh mengeluarkan isyarat berulang kali atau bertindak balas kepada perubahan yang disebabkan oleh bukan pemain, seperti pergerakan makhluk. dan item Jatuh, pertumbuhan tumbuhan, siang dan malam, dan banyak lagi. Oleh itu, dalam dunia saya, redstone boleh mengawal pelbagai jenis jentera, daripada jentera ringkas seperti pintu automatik, suis lampu dan bekalan kuasa strob, kepada lif besar, ladang automatik, platform permainan kecil dan juga komputer binaan dalam permainan . Baru-baru ini, stesen B UP utama @
 Drone yang boleh menahan angin kencang? Caltech menggunakan data penerbangan selama 12 minit untuk mengajar dron terbang mengikut angin
Apr 09, 2023 pm 11:51 PM
Drone yang boleh menahan angin kencang? Caltech menggunakan data penerbangan selama 12 minit untuk mengajar dron terbang mengikut angin
Apr 09, 2023 pm 11:51 PM
Apabila angin cukup kuat untuk meniup payung, drone itu stabil, seperti ini: Terbang dalam angin adalah sebahagian daripada terbang di udara Dari tahap yang besar, apabila juruterbang mendaratkan pesawat, kelajuan angin mungkin Membawa cabaran kepada mereka; pada tahap yang lebih kecil, angin kencang juga boleh menjejaskan penerbangan dron. Pada masa ini, dron sama ada diterbangkan dalam keadaan terkawal, tanpa angin, atau dikendalikan oleh manusia menggunakan alat kawalan jauh. Dron dikawal oleh penyelidik untuk terbang dalam formasi di langit terbuka, tetapi penerbangan ini biasanya dijalankan dalam keadaan dan persekitaran yang ideal. Walau bagaimanapun, agar dron melakukan tugasan yang perlu tetapi rutin secara autonomi, seperti menghantar pakej, ia mesti dapat menyesuaikan diri dengan keadaan angin dalam masa nyata. Untuk menjadikan dron lebih mudah dikendalikan apabila terbang mengikut angin, pasukan jurutera dari Caltech
 Berbilang laluan, berbilang domain, merangkumi semua! Google AI mengeluarkan model am pembelajaran berbilang domain MDL
May 28, 2023 pm 02:12 PM
Berbilang laluan, berbilang domain, merangkumi semua! Google AI mengeluarkan model am pembelajaran berbilang domain MDL
May 28, 2023 pm 02:12 PM
Model pembelajaran mendalam untuk tugas penglihatan (seperti klasifikasi imej) biasanya dilatih hujung ke hujung dengan data daripada domain visual tunggal (seperti imej semula jadi atau imej yang dijana komputer). Secara amnya, aplikasi yang menyelesaikan tugas penglihatan untuk berbilang domain perlu membina berbilang model untuk setiap domain yang berasingan dan melatihnya secara berasingan Data tidak dikongsi antara domain yang berbeza, setiap model akan mengendalikan data input tertentu. Walaupun ia berorientasikan kepada bidang yang berbeza, beberapa ciri lapisan awal antara model ini adalah serupa, jadi latihan bersama model ini adalah lebih cekap. Ini mengurangkan kependaman dan penggunaan kuasa, dan mengurangkan kos memori untuk menyimpan setiap parameter model Pendekatan ini dipanggil pembelajaran berbilang domain (MDL). Selain itu, model MDL juga boleh mengatasi prestasi tunggal
 1.3ms mengambil masa 1.3ms! Seni bina rangkaian neural mudah alih sumber terbuka terbaru Tsinghua RepViT
Mar 11, 2024 pm 12:07 PM
1.3ms mengambil masa 1.3ms! Seni bina rangkaian neural mudah alih sumber terbuka terbaru Tsinghua RepViT
Mar 11, 2024 pm 12:07 PM
Alamat kertas: https://arxiv.org/abs/2307.09283 Alamat kod: https://github.com/THU-MIG/RepViTRepViT berprestasi baik dalam seni bina ViT mudah alih dan menunjukkan kelebihan yang ketara. Seterusnya, kami meneroka sumbangan kajian ini. Disebutkan dalam artikel bahawa ViT ringan biasanya berprestasi lebih baik daripada CNN ringan pada tugas visual, terutamanya disebabkan oleh modul perhatian diri berbilang kepala (MSHA) mereka yang membolehkan model mempelajari perwakilan global. Walau bagaimanapun, perbezaan seni bina antara ViT ringan dan CNN ringan belum dikaji sepenuhnya. Dalam kajian ini, penulis menyepadukan ViT ringan ke dalam yang berkesan
 Adakah anda tahu bahawa pengaturcara akan merosot dalam beberapa tahun?
Nov 08, 2023 am 11:17 AM
Adakah anda tahu bahawa pengaturcara akan merosot dalam beberapa tahun?
Nov 08, 2023 am 11:17 AM
Majalah "ComputerWorld" pernah menulis artikel yang mengatakan bahawa "pengaturcaraan akan hilang menjelang 1960" kerana IBM membangunkan bahasa baharu FORTRAN, yang membolehkan jurutera menulis formula matematik yang mereka perlukan dan kemudian menyerahkannya kepada komputer, jadi pengaturcaraan tamat. Beberapa tahun kemudian, kami mendengar pepatah baru: mana-mana ahli perniagaan boleh menggunakan istilah perniagaan untuk menerangkan masalah mereka dan memberitahu komputer apa yang perlu dilakukan Menggunakan bahasa pengaturcaraan yang dipanggil COBOL ini, syarikat tidak lagi memerlukan pengaturcara. Kemudian, dikatakan bahawa IBM membangunkan bahasa pengaturcaraan baharu yang dipanggil RPG yang membolehkan pekerja mengisi borang dan menjana laporan, jadi kebanyakan keperluan pengaturcaraan syarikat dapat diselesaikan melaluinya.



