Anatomi Algoritma Pokok Keputusan
Penterjemah|. Zhao Qingyu
Pengulas| Sun Shujuan
Kata Pengantar
Dalam pembelajaran mesin, pengelasan mempunyai dua peringkat , ialah. peringkat pembelajaran dan peringkat ramalan masing-masing. Dalam fasa pembelajaran, model dibina berdasarkan data latihan yang diberikan dalam fasa ramalan, model digunakan untuk meramal tindak balas yang diberikan data. Pokok keputusan adalah salah satu algoritma pengelasan yang paling mudah untuk difahami dan dijelaskan.
Dalam pembelajaran mesin, pengelasan mempunyai dua peringkat iaitu peringkat pembelajaran dan peringkat ramalan. Dalam fasa pembelajaran, model dibina berdasarkan data latihan yang diberikan dalam fasa ramalan, model digunakan untuk meramal tindak balas yang diberikan data. Pokok keputusan adalah salah satu algoritma pengelasan yang paling mudah untuk difahami dan dijelaskan.
Algoritma pepohon keputusan
Algoritma pepohon keputusan ialah sejenis algoritma pembelajaran yang diselia. Tidak seperti algoritma pembelajaran diselia yang lain, algoritma pepohon keputusan boleh digunakan untuk menyelesaikan kedua-dua masalah regresi dan klasifikasi.
Tujuan menggunakan pepohon keputusan adalah untuk mencipta model latihan yang meramalkan kelas atau nilai pembolehubah sasaran dengan mempelajari peraturan keputusan mudah yang disimpulkan daripada data sebelumnya (data latihan).
Dalam pepohon keputusan, kita bermula dari akar pokok untuk meramalkan label kelas sesuatu rekod. Kami membandingkan nilai atribut akar dengan atribut yang direkodkan, dan berdasarkan perbandingan, kami mengikuti cawangan yang sepadan dengan nilai ini dan melompat ke nod seterusnya.
Jenis pepohon keputusan
Berdasarkan jenis pembolehubah sasaran yang kita ada, kita boleh membahagikan pepohon kepada dua jenis:
1 Pohon keputusan pembolehubah kategori: Ya Keputusan pokok pembolehubah sasaran kategori dipanggil pokok keputusan pembolehubah kategori.
2. Pepohon keputusan pembolehubah berterusan: Pembolehubah sasaran pepohon keputusan adalah berterusan, jadi ia dipanggil pepohon keputusan pembolehubah berterusan.
Contoh: Katakan kita mempunyai masalah untuk meramalkan sama ada pelanggan akan membayar premium pembaharuan kepada syarikat insurans. Pendapatan pelanggan ialah pembolehubah penting di sini, tetapi syarikat insurans tidak mempunyai butiran pendapatan untuk semua pelanggan. Sekarang setelah kita tahu ini adalah pembolehubah penting, kita kemudian boleh membina pepohon keputusan untuk meramalkan hasil pelanggan berdasarkan pekerjaan, produk dan pelbagai pembolehubah lain. Dalam kes ini, kami meramalkan bahawa pembolehubah sasaran adalah berterusan.
Istilah penting yang berkaitan dengan pepohon keputusan
1 Nod akar: Ia mewakili keseluruhan ahli atau sampel, yang akan dibahagikan lagi kepada dua atau lebih koleksi jenis yang sama.
2. Pemisahan): Proses pembahagian nod kepada dua atau lebih nod anak.
3. Nod Keputusan: Apabila nod anak berpecah kepada lebih banyak nod anak, ia dipanggil nod keputusan.
4. Daun / Nod Terminal: Nod yang tidak boleh dipecah dipanggil daun atau nod terminal.
5 Pemangkasan: Proses di mana kita memadamkan nod anak nod keputusan dipanggil pemangkasan. Pembinaan juga boleh dilihat sebagai proses pemisahan terbalik.
6. Cawangan/Sub-Pokok: Sub-bahagian daripada keseluruhan pokok dipanggil dahan atau sub-pokok.
7. Nod Ibu Bapa dan Anak: Nod yang boleh dipecahkan kepada nod anak dipanggil nod induk, dan nod anak ialah nod anak nod induk.
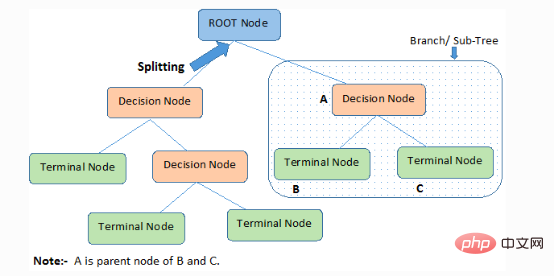
Pokok keputusan mengelaskan sampel dalam susunan menurun dari akar ke nod daun/terminal, yang menyediakan kaedah pengelasan sampel. Setiap nod dalam pepohon bertindak sebagai kes ujian untuk atribut tertentu, dan setiap arah menurun dari nod sepadan dengan jawapan yang mungkin untuk kes ujian. Proses ini bersifat rekursif dan dirawat secara sama untuk setiap subpokok yang berakar pada nod baharu.
Andaian yang dibuat semasa membuat pepohon keputusan
Berikut ialah beberapa andaian yang kami buat apabila menggunakan pepohon keputusan:
● Mula-mula, ambil keseluruhan set latihan sebagai punca.
●Nilai ciri sebaiknya dikelaskan. Jika nilai ini berterusan, ia boleh didiskritkan sebelum membina model.
●Rekod diedarkan secara rekursif berdasarkan nilai atribut.
● Dengan menggunakan beberapa kaedah statistik untuk meletakkan atribut yang sepadan pada nod akar pokok atau nod dalaman pokok mengikut susunan.
Pokok keputusan mengikut jumlah borang perwakilan produk. Jumlah Produk (SOP) juga dikenali sebagai bentuk normal disjungtif. Untuk kelas, setiap cawangan dari akar pokok ke nod daun dengan kelas yang sama ialah gabungan nilai, dan cawangan berbeza yang berakhir dalam kelas itu membentuk percabaran.
Cabaran utama dalam proses pelaksanaan pepohon keputusan adalah untuk menentukan atribut nod akar dan setiap nod peringkat Masalah ini ialah masalah pemilihan atribut. Pada masa ini terdapat kaedah pemilihan atribut yang berbeza untuk memilih atribut nod pada setiap peringkat.
Bagaimanakah pepohon keputusan berfungsi
Ciri-ciri pemisahan dalam membuat keputusan memberi kesan serius terhadap ketepatan pepohon, dan kriteria membuat keputusan bagi pepohon klasifikasi dan pepohon regresi adalah berbeza.
Pokok keputusan menggunakan pelbagai algoritma untuk memutuskan untuk membahagikan nod kepada dua atau lebih nod anak. Penciptaan nod kanak-kanak meningkatkan kehomogenan nod kanak-kanak. Dalam erti kata lain, ketulenan nod meningkat berbanding pembolehubah sasaran. Pepohon keputusan memisahkan nod pada semua pembolehubah yang tersedia dan kemudian memilih nod yang boleh menghasilkan banyak nod anak isomorfik untuk pemisahan.
Algoritma dipilih berdasarkan jenis pembolehubah sasaran. Seterusnya, mari kita lihat beberapa algoritma yang digunakan dalam pepohon keputusan:
ID3→(Sambungan D3)
C4.5→(Pengganti ID3)
CART→ (Pokok Pengelasan dan Regresi)
CHAID→(Pengesanan interaksi automatik Chi-square melakukan pemisahan berbilang peringkat apabila mengira pepohon pengelasan)
MARS →(Splines regresi adaptif berbilang)
Algoritma ID3 menggunakan kaedah carian tamak atas ke bawah untuk membina pepohon keputusan melalui ruang cawangan yang mungkin tanpa menjejak ke belakang. Algoritma tamak, seperti namanya, sentiasa membuat apa yang kelihatan sebagai pilihan terbaik pada masa tertentu.
Langkah algoritma ID3:
1 Ia menggunakan set asal S sebagai nod akar.
2 Semasa setiap lelaran algoritma, ulangi atribut yang tidak digunakan dalam set S dan hitung entropi (H) dan perolehan maklumat (IG) bagi atribut.
3. Kemudian pilih atribut dengan entropi terkecil atau keuntungan maklumat terbesar.
4. Kemudian pisahkan set S menggunakan atribut yang dipilih untuk menjana subset data.
5 Algoritma terus berulang pada setiap subset, hanya mengambil kira atribut yang tidak pernah dipilih sebelum ini pada setiap lelaran.
Kaedah Pemilihan Atribut
Jika set data mengandungi N atribut, maka memutuskan atribut mana yang hendak diletakkan pada nod akar atau pada peringkat pokok yang berbeza sebagai nod dalaman adalah satu langkah yang kompleks. Masalahnya tidak boleh diselesaikan dengan memilih mana-mana nod secara rawak sebagai nod akar. Jika kita menggunakan pendekatan rawak, kita mungkin mendapat keputusan yang lebih teruk.
Untuk menyelesaikan masalah pemilihan atribut ini, penyelidik telah mereka beberapa penyelesaian. Mereka mencadangkan menggunakan kriteria berikut:
- Entropi
- Peningkatan Maklumat
- Indeks Gini
- Kadar Keuntungan
- Pengurangan Varians
- Chi-Square
Kira nilai setiap atribut menggunakan kriteria ini, kemudian susun nilai dan letakkan atribut dalam pepohon mengikut tertib, iaitu atribut dengan nilai tertinggi diletakkan pada kedudukan akar.
Apabila menggunakan perolehan maklumat sebagai kriteria, kami menganggap bahawa atribut adalah kategori, manakala untuk indeks Gini, kami menganggap bahawa atribut adalah berterusan.
1. Entropi
Entropi ialah ukuran rawak maklumat yang sedang diproses. Semakin tinggi nilai entropi, semakin sukar untuk membuat sebarang kesimpulan daripada maklumat. Melambung syiling ialah contoh tingkah laku yang memberikan maklumat rawak.
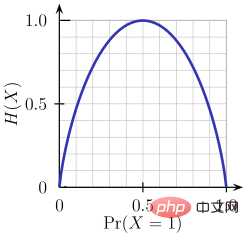
Seperti yang dapat dilihat daripada rajah di atas, apabila kebarangkalian ialah 0 atau 1, entropi H(X) ialah sifar. Entropi adalah paling besar apabila kebarangkalian adalah 0.5 kerana ia menunjukkan rawak lengkap dalam data.
Peraturan yang diikuti oleh ID3 ialah: cawangan dengan entropi 0 ialah nod daun, dan cawangan dengan entropi lebih besar daripada 0 perlu diasingkan lagi.
Entropi matematik bagi satu atribut dinyatakan seperti berikut:

di mana S mewakili keadaan semasa, Pi mewakili kebarangkalian peristiwa i dalam keadaan S atau i dalam peratusan Kelas nod S keadaan.
Entropi matematik berbilang atribut dinyatakan seperti berikut:
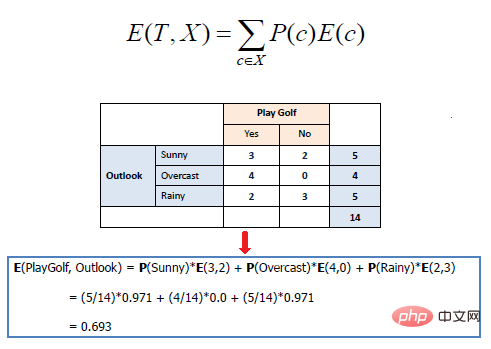
di mana T mewakili keadaan semasa dan X mewakili atribut yang dipilih
2. Keuntungan Maklumat
Pendapatan maklumat (IG) ialah atribut statistik yang digunakan untuk mengukur kesan latihan berasingan untuk atribut yang diberikan mengikut kelas sasaran. Membina pepohon keputusan ialah proses mencari atribut yang mengembalikan perolehan maklumat tertinggi dan entropi terendah.
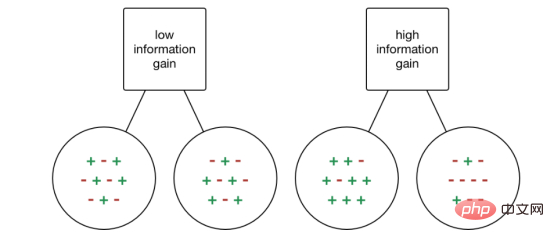
Peningkatan maklumat ialah penurunan entropi. Ia mengira perbezaan entropi sebelum pemisahan set data dan purata perbezaan entropi selepas pemisahan berdasarkan nilai atribut yang diberikan. Algoritma pepohon keputusan ID3 menggunakan kaedah perolehan maklumat.
IG dinyatakan secara matematik seperti berikut:

Dengan pendekatan yang lebih mudah, kita boleh membuat kesimpulan ini:
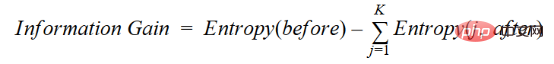
Di mana sebelum ini adalah set data sebelum pemisahan, K ialah bilangan subset yang dijana oleh pemisahan dan (j, selepas) ialah subset j selepas pemisahan.
3. Indeks Gini
Anda boleh memahami indeks Gini sebagai fungsi kos untuk menilai pengasingan dalam set data. Ia dikira dengan menolak jumlah kebarangkalian kuasa dua untuk setiap kelas daripada 1. Ia memihak kepada kes sekatan yang lebih besar dan lebih mudah untuk dilaksanakan, manakala perolehan maklumat memihak kepada kes sekatan yang lebih kecil dengan nilai yang berbeza.
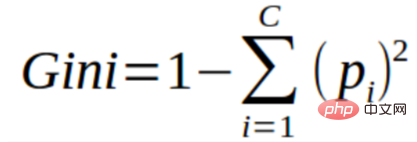
Indeks Gini tidak dapat dipisahkan daripada pembolehubah sasaran kategori "kejayaan" atau "kegagalan". Ia hanya melakukan pemisahan binari. Semakin tinggi pekali Gini, semakin tinggi tahap ketaksamaan dan semakin kuat heterogenitinya.
Langkah-langkah untuk mengira pemisahan indeks Gini adalah seperti berikut:
- Kira pekali Gini nod anak, menggunakan kejayaan di atas (p) dan Formula untuk kegagalan (q) ialah (p²+q²).
- Kira indeks pekali Gini pemisahan menggunakan skor Gini berwajaran setiap nod pemisahan.
CART (Pokok Klasifikasi dan Regresi) menggunakan kaedah indeks Gini untuk mencipta titik pemisah.
4. Kadar keuntungan
Perolehan maklumat cenderung memilih atribut dengan sejumlah besar nilai sebagai nod akar. Ini bermakna ia lebih suka sifat dengan sejumlah besar nilai berbeza.
C4.5 ialah kaedah ID3 yang dipertingkatkan, yang menggunakan nisbah keuntungan, yang merupakan pengubahsuaian keuntungan maklumat untuk mengurangkan berat sebelahnya, yang biasanya merupakan kaedah pilihan terbaik. Kadar keuntungan mengatasi masalah perolehan maklumat dengan mengambil kira bilangan cawangan sebelum melakukan pembahagian. Ia membetulkan untuk mendapatkan maklumat dengan mengambil kira maklumat intrinsik yang berasingan.
Andaikan kami mempunyai set data yang mengandungi pengguna dan pilihan genre filem mereka berdasarkan pembolehubah seperti jantina, kumpulan umur, kelas, dsb. Dengan bantuan perolehan maklumat anda akan memisahkan dalam "Jantina" (dengan andaian ia mempunyai keuntungan maklumat tertinggi), kini pembolehubah "Kumpulan Umur" dan "Penilaian" mungkin sama penting, dengan bantuan nisbah keuntungan kita boleh memilih Hartanah yang dipisahkan dalam lapisan seterusnya.
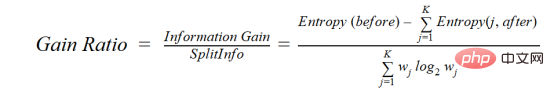
di mana sebelum ini adalah set data sebelum pemisahan, K ialah bilangan subset yang dijana oleh pemisahan, (j, selepas) ialah subset selepas pemisahan j.
5. Pengurangan varians
Pengurangan varians ialah algoritma yang digunakan untuk pembolehubah sasaran berterusan (masalah regresi). Algoritma menggunakan formula varians standard untuk memilih pemisahan terbaik. Pilih pemisahan dengan varians yang lebih rendah sebagai kriteria untuk memisahkan populasi:
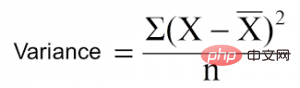
ialah min, X ialah nilai sebenar dan n ialah nombor daripada nilai.
Langkah untuk mengira varians:
- Kira varians setiap nod.
- Kira varians setiap pemisahan dan gunakannya sebagai purata wajaran varians setiap nod.
6. Chi-square
CHAID ialah singkatan Chi-squared Automatic Interaction Detector. Ini adalah salah satu kaedah pengelasan pokok yang lebih lama. Cari perbezaan ketara secara statistik antara nod anak dan nod induknya. Kami mengukurnya dengan jumlah perbezaan kuasa dua antara frekuensi yang diperhatikan dan dijangka pembolehubah sasaran.
Ia berfungsi dengan pembolehubah sasaran kategori "Kejayaan" atau "Kegagalan". Ia boleh melakukan dua atau lebih pemisahan. Lebih tinggi nilai khi kuasa dua, lebih ketara secara statistik perbezaan antara nod anak dan nod induk. Ia menjana pokok yang dipanggil CHAID.
Secara matematik, Khi kuasa dua dinyatakan sebagai:

Langkah-langkah untuk mengira Khi kuasa dua ialah seperti berikut:
- Hitung khi kuasa dua satu nod dengan mengira sisihan untuk kejayaan dan kegagalan
- Gunakan kejayaan yang berasingan dan kegagalan untuk setiap nod Jumlah semua khi kuasa dua mengira khi kuasa dua yang dipisahkan
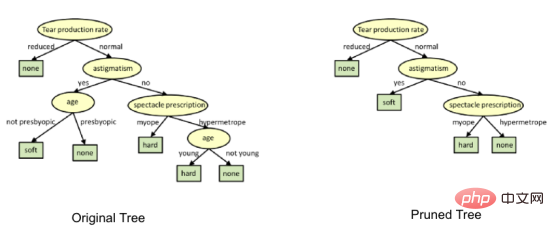
Bagaimana untuk mengelakkan/melawan keterlaluan pepohon keputusan?
Terdapat pepohon keputusan Masalah biasa, terutamanya dengan pokok yang penuh dengan lajur. Kadang-kadang kelihatan seperti pokok itu menghafal set data latihan. Jika pepohon keputusan tidak mempunyai kekangan, ia akan memberi anda ketepatan 100% pada set data latihan, kerana dalam kes yang paling teruk, ia akan menghasilkan satu daun untuk setiap pemerhatian. Oleh itu, ini menjejaskan ketepatan apabila meramalkan sampel yang bukan sebahagian daripada set latihan.
Di sini saya memperkenalkan dua kaedah untuk menghapuskan overfitting iaitu pemangkasan pokok keputusan dan hutan rawak.
1. Pemangkasan pokok keputusan
Proses pengasingan akan menghasilkan pokok yang tumbuh sepenuhnya sehingga kriteria berhenti dicapai. Walau bagaimanapun, pokok matang berkemungkinan melampaui data, mengakibatkan ketepatan yang lemah pada data yang tidak kelihatan.

import numpy as np import matplotlib.pyplot as plt import pandas as pd
Selepas itu, kami menggunakan kaedah berikut untuk memuatkan set data. Ia termasuk 5 atribut, id pengguna, jantina, umur, anggaran gaji dan status pembelian.
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()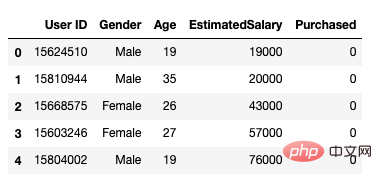
Rajah 1 Set Data
Kami hanya menukar umur dan anggaran gaji sebagai pembolehubah bebas kami
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
Langkah seterusnya ialah mengasingkan set data kepada set latihan dan ujian.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
Seterusnya, lakukan penskalaan ciri
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
Betulkan model menjadi pengelas pokok keputusan.
from sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
Buat ramalan dan semak ketepatan.
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))Pengelas pokok keputusan mempunyai ketepatan 91%.
Matriks Kekeliruan
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()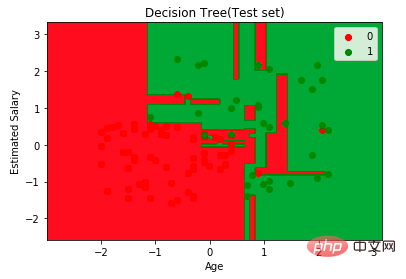
Seterusnya anda boleh menggunakan fungsi export_graphviz Scikit-learn untuk memaparkan pokok dalam buku nota Jupyter. Untuk melukis pepohon, kita perlu memasang Graphviz dan pydotplus menggunakan arahan berikut:
conda install python-graphviz pip install pydotplus
from sklearn.tree import export_graphviz from sklearn.externals.six import StringIO from IPython.display import Image import pydotplusdot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True,feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
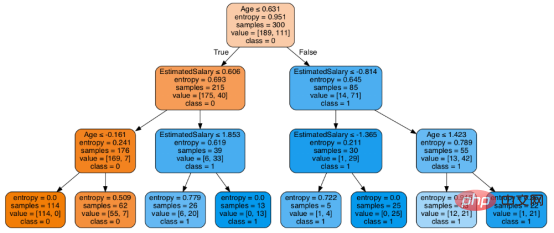
上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
Atas ialah kandungan terperinci Anatomi Algoritma Pokok Keputusan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 15 alat anotasi imej percuma sumber terbuka disyorkan
Mar 28, 2024 pm 01:21 PM
15 alat anotasi imej percuma sumber terbuka disyorkan
Mar 28, 2024 pm 01:21 PM
Anotasi imej ialah proses mengaitkan label atau maklumat deskriptif dengan imej untuk memberi makna dan penjelasan yang lebih mendalam kepada kandungan imej. Proses ini penting untuk pembelajaran mesin, yang membantu melatih model penglihatan untuk mengenal pasti elemen individu dalam imej dengan lebih tepat. Dengan menambahkan anotasi pada imej, komputer boleh memahami semantik dan konteks di sebalik imej, dengan itu meningkatkan keupayaan untuk memahami dan menganalisis kandungan imej. Anotasi imej mempunyai pelbagai aplikasi, meliputi banyak bidang, seperti penglihatan komputer, pemprosesan bahasa semula jadi dan model penglihatan graf Ia mempunyai pelbagai aplikasi, seperti membantu kenderaan dalam mengenal pasti halangan di jalan raya, dan membantu dalam proses. pengesanan dan diagnosis penyakit melalui pengecaman imej perubatan. Artikel ini terutamanya mengesyorkan beberapa alat anotasi imej sumber terbuka dan percuma yang lebih baik. 1.Makesen
 Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Dalam bidang pembelajaran mesin dan sains data, kebolehtafsiran model sentiasa menjadi tumpuan penyelidik dan pengamal. Dengan aplikasi meluas model yang kompleks seperti kaedah pembelajaran mendalam dan ensemble, memahami proses membuat keputusan model menjadi sangat penting. AI|XAI yang boleh dijelaskan membantu membina kepercayaan dan keyakinan dalam model pembelajaran mesin dengan meningkatkan ketelusan model. Meningkatkan ketelusan model boleh dicapai melalui kaedah seperti penggunaan meluas pelbagai model yang kompleks, serta proses membuat keputusan yang digunakan untuk menerangkan model. Kaedah ini termasuk analisis kepentingan ciri, anggaran selang ramalan model, algoritma kebolehtafsiran tempatan, dsb. Analisis kepentingan ciri boleh menerangkan proses membuat keputusan model dengan menilai tahap pengaruh model ke atas ciri input. Anggaran selang ramalan model
 Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Dalam istilah orang awam, model pembelajaran mesin ialah fungsi matematik yang memetakan data input kepada output yang diramalkan. Secara lebih khusus, model pembelajaran mesin ialah fungsi matematik yang melaraskan parameter model dengan belajar daripada data latihan untuk meminimumkan ralat antara output yang diramalkan dan label sebenar. Terdapat banyak model dalam pembelajaran mesin, seperti model regresi logistik, model pepohon keputusan, model mesin vektor sokongan, dll. Setiap model mempunyai jenis data dan jenis masalah yang berkenaan. Pada masa yang sama, terdapat banyak persamaan antara model yang berbeza, atau terdapat laluan tersembunyi untuk evolusi model. Mengambil perceptron penyambung sebagai contoh, dengan meningkatkan bilangan lapisan tersembunyi perceptron, kita boleh mengubahnya menjadi rangkaian neural yang mendalam. Jika fungsi kernel ditambah pada perceptron, ia boleh ditukar menjadi SVM. yang ini
 Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Artikel ini akan memperkenalkan cara mengenal pasti pemasangan lampau dan kekurangan dalam model pembelajaran mesin secara berkesan melalui keluk pembelajaran. Underfitting dan overfitting 1. Overfitting Jika model terlampau latihan pada data sehingga ia mempelajari bunyi daripadanya, maka model tersebut dikatakan overfitting. Model yang dipasang terlebih dahulu mempelajari setiap contoh dengan sempurna sehingga ia akan salah mengklasifikasikan contoh yang tidak kelihatan/baharu. Untuk model terlampau, kami akan mendapat skor set latihan yang sempurna/hampir sempurna dan set pengesahan/skor ujian yang teruk. Diubah suai sedikit: "Punca overfitting: Gunakan model yang kompleks untuk menyelesaikan masalah mudah dan mengekstrak bunyi daripada data. Kerana set data kecil sebagai set latihan mungkin tidak mewakili perwakilan yang betul bagi semua data. 2. Underfitting Heru
 Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Pada tahun 1950-an, kecerdasan buatan (AI) dilahirkan. Ketika itulah penyelidik mendapati bahawa mesin boleh melakukan tugas seperti manusia, seperti berfikir. Kemudian, pada tahun 1960-an, Jabatan Pertahanan A.S. membiayai kecerdasan buatan dan menubuhkan makmal untuk pembangunan selanjutnya. Penyelidik sedang mencari aplikasi untuk kecerdasan buatan dalam banyak bidang, seperti penerokaan angkasa lepas dan kelangsungan hidup dalam persekitaran yang melampau. Penerokaan angkasa lepas ialah kajian tentang alam semesta, yang meliputi seluruh alam semesta di luar bumi. Angkasa lepas diklasifikasikan sebagai persekitaran yang melampau kerana keadaannya berbeza daripada di Bumi. Untuk terus hidup di angkasa, banyak faktor mesti dipertimbangkan dan langkah berjaga-jaga mesti diambil. Para saintis dan penyelidik percaya bahawa meneroka ruang dan memahami keadaan semasa segala-galanya boleh membantu memahami cara alam semesta berfungsi dan bersedia untuk menghadapi kemungkinan krisis alam sekitar
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 AI yang boleh dijelaskan: Menerangkan model AI/ML yang kompleks
Jun 03, 2024 pm 10:08 PM
AI yang boleh dijelaskan: Menerangkan model AI/ML yang kompleks
Jun 03, 2024 pm 10:08 PM
Penterjemah |. Disemak oleh Li Rui |. Chonglou Model kecerdasan buatan (AI) dan pembelajaran mesin (ML) semakin kompleks hari ini, dan output yang dihasilkan oleh model ini adalah kotak hitam – tidak dapat dijelaskan kepada pihak berkepentingan. AI Boleh Dijelaskan (XAI) bertujuan untuk menyelesaikan masalah ini dengan membolehkan pihak berkepentingan memahami cara model ini berfungsi, memastikan mereka memahami cara model ini sebenarnya membuat keputusan, dan memastikan ketelusan dalam sistem AI, Amanah dan akauntabiliti untuk menyelesaikan masalah ini. Artikel ini meneroka pelbagai teknik kecerdasan buatan (XAI) yang boleh dijelaskan untuk menggambarkan prinsip asasnya. Beberapa sebab mengapa AI boleh dijelaskan adalah penting Kepercayaan dan ketelusan: Untuk sistem AI diterima secara meluas dan dipercayai, pengguna perlu memahami cara keputusan dibuat
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada




