
Helo semua, saya Peter~
Maklumat tentang pelbagai algoritma pengurangan dimensi di Internet adalah bercampur-campur, dan kebanyakannya tidak menyediakan kod sumber. Berikut ialah projek GitHub yang menggunakan Python untuk melaksanakan 11 algoritma pengekstrakan data klasik (pengurangan dimensi data), termasuk: PCA, LDA, MDS, LLE, TSNE, dsb., dengan maklumat yang berkaitan dan kesan paparan sangat sesuai untuk pembelajaran mesin dan mereka yang baru memulakan perlombongan data.
Pengurangan dimensi yang dipanggil ialah menggunakan set vektor Zi dengan nombor d untuk mewakili maklumat berguna yang terkandung dalam vektor Xi dengan nombor D, di mana d
Biasanya, kita akan mendapati bahawa dimensi kebanyakan set data ialah ratusan atau bahkan ribuan, dan dimensi MNIST klasik ialah 64.

Set data digit tulisan tangan MNIST
Tetapi dalam aplikasi sebenar, maklumat berguna yang kami gunakan tidak memerlukan dimensi yang begitu tinggi, dan setiap peningkatan Bilangan sampel diperlukan untuk satu dimensi meningkat secara eksponen, yang secara langsung boleh menyebabkan "bencana dimensi" yang besar boleh dicapai:
Alih keluar hingar Setelah kami dapat memproses maklumat ini dengan betul dan melakukan pengurangan dimensi dengan betul dan berkesan, ini akan membantu mengurangkan jumlah pengiraan dan dengan itu meningkatkan kecekapan pengendalian mesin. Pengurangan dimensi data juga sering digunakan dalam bidang seperti pemprosesan teks, pengecaman muka, pengecaman imej dan pemprosesan bahasa semula jadi.
Selalunya data dalam ruang berdimensi tinggi akan jarang diedarkan, jadi semasa proses pengurangan dimensi, kami biasanya melakukan beberapa pemadaman data ini termasuk data Lewah, tidak sah maklumat, ungkapan berulang, dsb. dihapuskan.
Contohnya: Terdapat gambar 1024*1024 Kecuali untuk kawasan 50*50 di tengah, semua kedudukan lain mempunyai nilai sifar ini boleh diklasifikasikan sebagai maklumat yang tidak berguna bahagian simetri maklumat boleh dikelaskan sebagai maklumat berulang.
Oleh itu, kebanyakan teknik pengurangan dimensi klasik juga dibangunkan berdasarkan kandungan ini kaedah pengurangan dimensi terbahagi kepada pengurangan dimensi bukan linear dibahagikan kepada kaedah berasaskan fungsi dan nilai eigen.
Berdasarkan Kaedah pengurangan dimensi bukan linear bagi fungsi kernel - KPCA, KICA, KDA
Kaedah pengurangan dimensi bukan linear berdasarkan nilai eigen (pembelajaran corak aliran) - ISOMAP, LLE, LE, LPP, LTSA, MVU
Heucoder , pelajar sarjana dalam bidang teknologi komputer di Institut Teknologi Harbin, menyusun sejumlah 12 algoritma pengurangan dimensi klasik termasuk PCA, KPCA, LDA, MDS, ISOMAP, LLE, TSNE, AutoEncoder, FastICA, SVD, LE, dan LPP maklumat, kod dan paparan disediakan Yang berikut terutamanya akan menggunakan algoritma PCA sebagai contoh untuk memperkenalkan operasi khusus algoritma pengurangan dimensi.
PCA ialah kaedah pemetaan berdasarkan pemetaan daripada ruang berdimensi tinggi kepada ruang berdimensi rendah Ia juga merupakan algoritma pengurangan dimensi tanpa pengawasan yang paling asas . Ia telah dicadangkan oleh Karl Pearson pada tahun 1901 dan merupakan kaedah pengurangan dimensi linear. Prinsip yang dikaitkan dengan PCA sering dipanggil teori varians maksimum atau teori ralat minimum. Kedua-duanya mempunyai matlamat yang sama, tetapi fokus proses adalah berbeza.
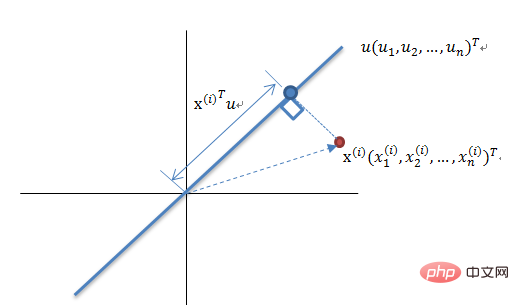
Prinsip Pengurangan Dimensi Teori Varians Maksimum
Mengurangkan set vektor N-dimensi kepada K-dimensi (K lebih besar daripada 0, kurang daripada N), matlamatnya adalah untuk memilih tapak ortogonal unit K, COV(X,Y) bagi setiap medan ialah 0, dan varians medan adalah sebesar mungkin. Oleh itu, varians maksimum bermakna varians data unjuran dimaksimumkan Dalam proses ini, kita perlu mencari ruang unjuran terbaik Wnxk, matriks kovarians, dan lain-lain set data Xmxn Aliran algoritma ialah:
Ralat minimum ialah unjuran linear yang meminimumkan kos unjuran purata Dalam proses ini, kita perlu mencari parameter seperti fungsi penilaian ralat kuasa dua J0(x0).
Kod untuk algoritma PCA adalah seperti berikut:
from __future__ import print_function
from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.cm as cmx
import matplotlib.colors as colors
import numpy as np
%matplotlib inline
def shuffle_data(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
# 正规化数据集 X
def normalize(X, axis=-1, p=2):
lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
lp_norm[lp_norm == 0] = 1
return X / np.expand_dims(lp_norm, axis)
# 标准化数据集 X
def standardize(X):
X_std = np.zeros(X.shape)
mean = X.mean(axis=0)
std = X.std(axis=0)
# 做除法运算时请永远记住分母不能等于 0 的情形
# X_std = (X - X.mean(axis=0)) / X.std(axis=0)
for col in range(np.shape(X)[1]):
if std[col]:
X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
return X_std
# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
if shuffle:
X, y = shuffle_data(X, y, seed)
n_train_samples = int(X.shape[0] * (1-test_size))
x_train, x_test = X[:n_train_samples], X[n_train_samples:]
y_train, y_test = y[:n_train_samples], y[n_train_samples:]
return x_train, x_test, y_train, y_test
# 计算矩阵 X 的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
if not Y.any():
Y = X
n_samples = np.shape(X)[0]
covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
return np.array(covariance_matrix, dtype=float)
# 计算数据集 X 每列的方差
def calculate_variance(X):
n_samples = np.shape(X)[0]
variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
return variance
# 计算数据集 X 每列的标准差
def calculate_std_dev(X):
std_dev = np.sqrt(calculate_variance(X))
return std_dev
# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
# 先计算协方差矩阵
covariance_matrix = calculate_covariance_matrix(X, Y)
# 计算 X, Y 的标准差
std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
return np.array(correlation_matrix, dtype=float)
class PCA():
"""
主成份分析算法 PCA,非监督学习算法.
"""
def __init__(self):
self.eigen_values = None
self.eigen_vectors = None
self.k = 2
def transform(self, X):
"""
将原始数据集 X 通过 PCA 进行降维
"""
covariance = calculate_covariance_matrix(X)
# 求解特征值和特征向量
self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
# 将特征值从大到小进行排序,注意特征向量是按列排的,即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量
idx = self.eigen_values.argsort()[::-1]
eigenvalues = self.eigen_values[idx][:self.k]
eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
# 将原始数据集 X 映射到低维空间
X_transformed = X.dot(eigenvectors)
return X_transformed
def main():
# Load the dataset
data = datasets.load_iris()
X = data.data
y = data.target
# 将数据集 X 映射到低维空间
X_trans = PCA().transform(X)
x1 = X_trans[:, 0]
x2 = X_trans[:, 1]
cmap = plt.get_cmap('viridis')
colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
class_distr = []
# Plot the different class distributions
for i, l in enumerate(np.unique(y)):
_x1 = x1[y == l]
_x2 = x2[y == l]
_y = y[y == l]
class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
# Add a legend
plt.legend(class_distr, y, loc=1)
# Axis labels
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
if __name__ == "__main__":
main()Akhir sekali, kita akan mendapat hasil pengurangan dimensi seperti berikut. Antaranya, jika anda mendapat bahawa apabila bilangan ciri (D) jauh lebih besar daripada bilangan sampel (N), anda boleh menggunakan sedikit helah untuk melaksanakan penukaran kerumitan algoritma PCA.
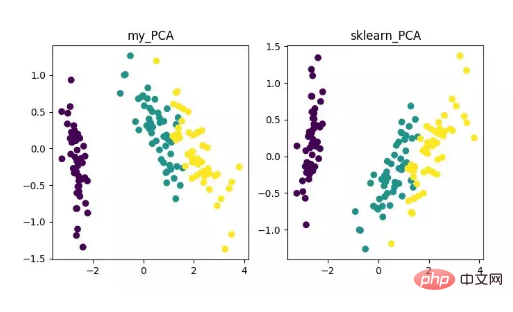
Paparan algoritma pengurangan dimensi PCA
Sudah tentu, walaupun algoritma ini klasik dan biasa digunakan, kelemahannya juga sangat jelas. Ia boleh menghapuskan korelasi linear dengan sangat baik, tetapi apabila berhadapan dengan korelasi peringkat tinggi, kesannya adalah buruk pada masa yang sama, premis pelaksanaan PCA adalah untuk menganggap bahawa ciri-ciri utama data diedarkan dalam arah ortogonal, jadi; untuk arah bukan ortogon Terdapat beberapa arah dengan varians yang besar, dan kesan PCA akan dikurangkan dengan banyak.
KPCA ialah produk gabungan teknologi kernel dan PCA Ia terutamanya berkaitan dengan PCA Perbezaannya ialah fungsi kernel digunakan semasa mengira matriks kovarians, iaitu matriks kovarians selepas pemetaan oleh fungsi kernel.
Pengenalan fungsi kernel dapat menyelesaikan masalah pemetaan data tak linear dengan berkesan. kPCA boleh memetakan data tak linear ke ruang dimensi tinggi, di mana PCA standard digunakan untuk memetakannya ke ruang dimensi rendah yang lain.
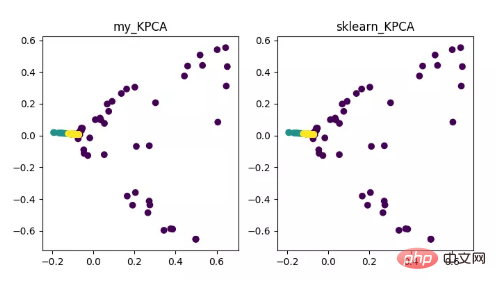
Paparan algoritma pengurangan dimensi KPCA
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master /codes/PCA/KPCA.py
LDA ialah teknologi yang boleh digunakan sebagai pengekstrakan ciri dan matlamatnya adalah untuk memaksimumkan kelas Perbezaan antara kelas, meminimumkan unjuran arah perbezaan dalam kelas, untuk memudahkan tugas seperti pengelasan, iaitu, untuk memisahkan sampel kelas yang berbeza dengan berkesan. LDA boleh meningkatkan kecekapan pengiraan dalam proses analisis data, dan boleh mengurangkan overfitting yang disebabkan oleh bencana dimensi untuk model yang tidak boleh diselaraskan.
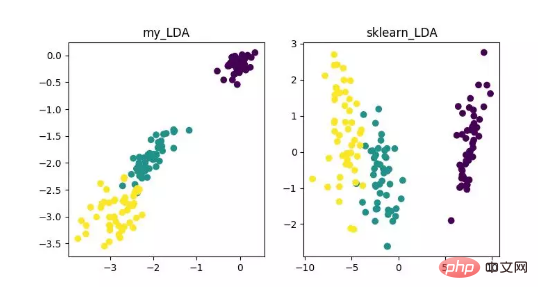
Paparan algoritma pengurangan dimensi LDA
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master /codes/LDA
MDS ialah analisis penskalaan pelbagai dimensi Ia merupakan kaedah yang menyatakan persepsi dan keutamaan objek kajian melalui rajah spatial intuitif. Kaedah pengurangan dimensi tradisional. Kaedah ini mengira jarak antara mana-mana dua titik sampel, supaya jarak relatif boleh dikekalkan selepas unjuran ke dalam ruang berdimensi rendah untuk mencapai unjuran.
Memandangkan MDS dalam sklearn menggunakan kaedah pengoptimuman berulang, kedua-dua kaedah berulang dan bukan lelaran dilaksanakan di bawah.
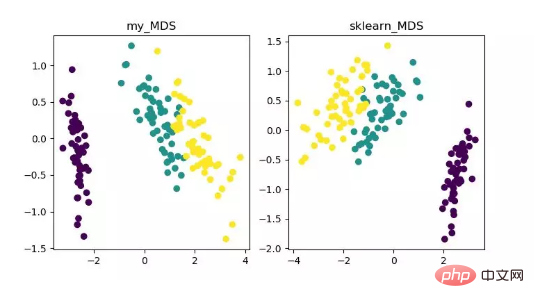
Paparan algoritma pengurangan dimensi MDS
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master /codes/MDS
Isomap ialah algoritma pemetaan ekuimetrik, yang boleh menyelesaikan dengan baik kelemahan algoritma MDS pada set data berstruktur bukan linear.
Algoritma MDS mengekalkan jarak antara sampel selepas pengurangan dimensi tidak berubah, manakala algoritma Isomap memperkenalkan graf kejiranan hanya disambungkan ke sampel bersebelahan mereka, mengira jarak antara titik jiran, dan kemudian menambahkannya di sini Aktif asas pengurangan dimensi dan pemeliharaan jarak.
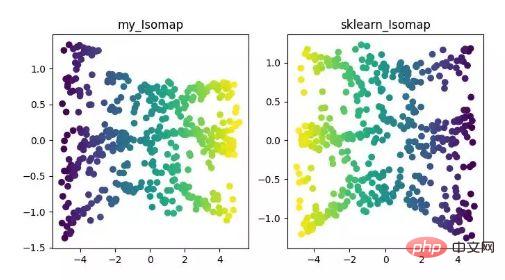
Paparan algoritma pengurangan dimensi ISOMAP
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master /codes/ISOMAP
LLE (pembenaman linear tempatan)LLE ialah algoritma pembenaman linear tempatan, yang merupakan algoritma pengurangan dimensi bukan linear. Idea teras algoritma ini ialah setiap titik boleh dibina semula secara lebih kurang dengan gabungan linear berbilang titik bersebelahan, dan kemudian data dimensi tinggi diunjurkan ke dalam ruang dimensi rendah untuk mengekalkan pembinaan semula linear tempatan antara titik data. . hubungan, iaitu, mempunyai pekali pembinaan semula yang sama. Apabila berurusan dengan pengurangan dimensi manifold yang dipanggil, kesannya jauh lebih baik daripada PCA.
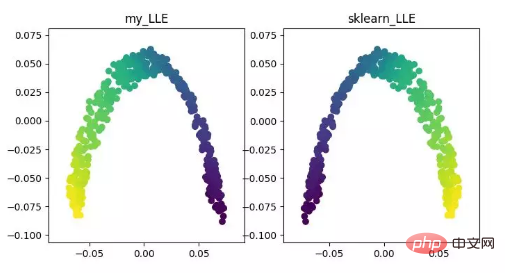
Paparan algoritma pengurangan dimensi LLE
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LLE
t-SNE juga merupakan algoritma pengurangan dimensi tak linear, yang sangat sesuai untuk mengurangkan data berdimensi tinggi kepada 2 atau 3 dimensi untuk visualisasi. Ia ialah algoritma pembelajaran mesin tanpa pengawasan yang membina semula aliran data dalam latitud rendah (dua atau tiga dimensi) berdasarkan aliran asal data.
Paparan hasil berikut merujuk kepada kod sumber, dan juga boleh dilaksanakan dengan aliran tensor (tidak perlu mengemas kini parameter secara manual).
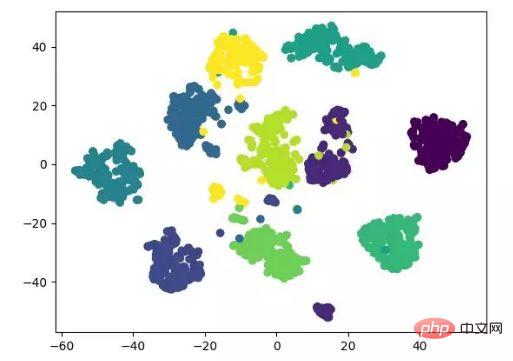
paparan algoritma pengurangan dimensi t-SNE
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree /master/codes/T-SNE
LE ialah Laplacian Eigenmap, yang agak serupa dengan algoritma LLE dan juga berdasarkan tempatan Dari perspektif membina hubungan antara data. Idea intuitifnya adalah untuk berharap bahawa titik yang berkaitan antara satu sama lain (titik yang disambungkan dalam graf) adalah sedekat mungkin dalam ruang yang dikurangkan secara dimensi dengan cara ini, penyelesaian yang mencerminkan struktur geometri manifold boleh diperolehi.
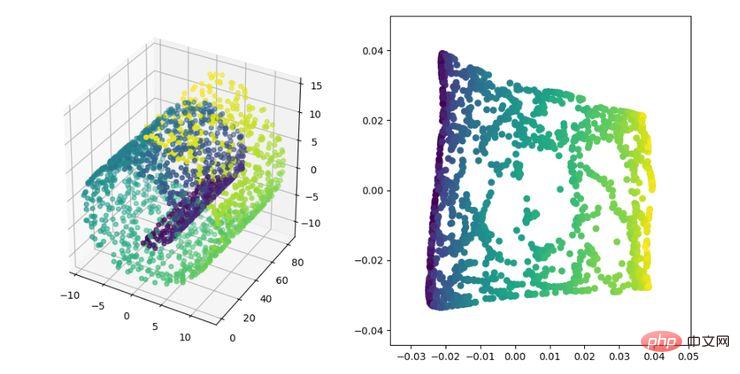
Paparan algoritma pengurangan dimensi LE
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master /codes/LE
LPP ialah algoritma unjuran pemeliharaan lokaliti. Ideanya adalah serupa dengan pemetaan ciri Laplacian lulus Adalah lebih baik untuk mengekalkan maklumat struktur jiran set data untuk membina pemetaan unjuran, tetapi LPP berbeza daripada LE dalam mendapatkan hasil unjuran secara langsung, yang memerlukan penyelesaian matriks unjuran.
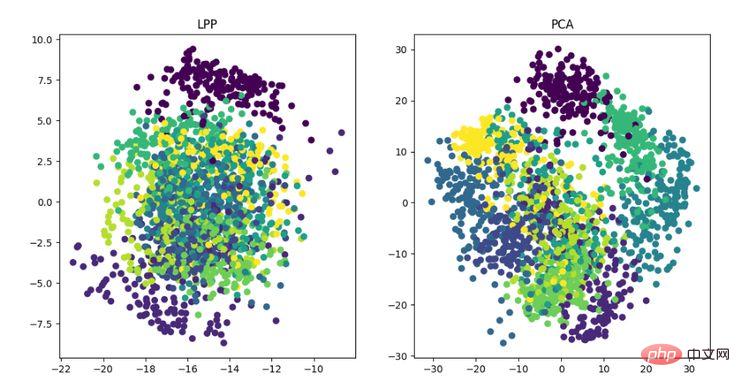
Paparan algoritma pengurangan dimensi LPP
Alamat kod:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master /codes/LPP
Heucoder kini merupakan pelajar sarjana dalam teknologi komputer di Harbin Institute of Technology, terutamanya aktif dalam medan Internet, Zhihu Nama panggilannya ialah "Super Love Learning", dan alamat halaman utama githubnya ialah: https://github.com/heucoder.
Alamat projek Github:
https://github.com/heucoder/dimensionality_reduction_alo_codes
Atas ialah kandungan terperinci Python melaksanakan algoritma pengurangan 12 dimensi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




