Peranti teknologi
Peranti teknologi
 AI
AI
 Sebuah artikel membincangkan secara ringkas keupayaan generalisasi pembelajaran mendalam
Sebuah artikel membincangkan secara ringkas keupayaan generalisasi pembelajaran mendalam
Sebuah artikel membincangkan secara ringkas keupayaan generalisasi pembelajaran mendalam

1. Isu keupayaan generalisasi DNN
Kertas ini terutamanya membincangkan mengapa model rangkaian saraf lebih parameter masih boleh mempunyai generalisasi yang baik? Iaitu, ia bukan sekadar menghafal set latihan, tetapi meringkaskan peraturan am dari set latihan, supaya ia boleh disesuaikan dengan set ujian (keupayaan generalisasi).

Ambil model pepohon keputusan klasik sebagai contoh Apabila model pepohon mempelajari peraturan am set data: situasi yang baik, jika pepohon mula-mula membelah nod, Ia hanya boleh membezakan sampel dengan label yang berbeza, kedalamannya sangat kecil, dan bilangan sampel pada setiap daun yang sepadan adalah mencukupi (iaitu, jumlah asas data untuk peraturan statistik juga agak besar), maka peraturan yang akan yang diperolehi akan lebih mungkin digeneralisasikan kepada data lain. (iaitu: kesesuaian yang baik dan keupayaan generalisasi).
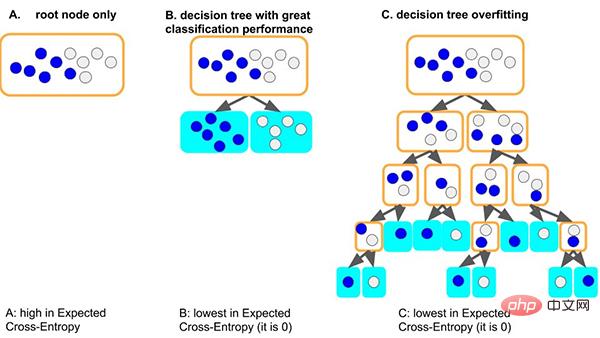
Situasi lain yang lebih teruk ialah jika pokok tidak dapat mempelajari beberapa peraturan am, untuk mempelajari set data ini, pokok akan menjadi lebih dalam dan lebih dalam, mungkin setiap kali Setiap daun nod sepadan dengan sebilangan kecil sampel (maklumat statistik yang dibawa oleh sejumlah kecil data mungkin hanya bunyi bising Akhirnya, semua data dihafal dengan hafalan (iaitu: overfitting dan tiada keupayaan generalisasi). Kita dapat melihat bahawa model pokok yang terlalu dalam dengan mudah boleh menjadi terlalu muat.
Jadi, bagaimanakah rangkaian neural terparameter boleh mencapai generalisasi yang baik?
2. Sebab keupayaan generalisasi DNN
Artikel ini menerangkan dari perspektif yang mudah dan umum - meneroka sebab keupayaan generalisasi dalam proses pengoptimuman keturunan kecerunan rangkaian saraf:
Kami meringkaskan teori koheren kecerunan: koheren kecerunan daripada sampel yang berbeza adalah sebab mengapa rangkaian saraf boleh mempunyai keupayaan generalisasi yang baik. Apabila kecerunan sampel yang berbeza diselaraskan dengan baik semasa latihan, iaitu, apabila ia koheren, keturunan kecerunan adalah stabil, boleh menumpu dengan cepat, dan model yang terhasil boleh digeneralisasikan dengan baik. Jika tidak, jika sampel terlalu sedikit atau masa latihan terlalu lama, ia mungkin tidak digeneralisasikan.

Berdasarkan teori ini, kita boleh membuat penjelasan berikut.
2.1 Generalisasi Rangkaian Neural Lebar
Model rangkaian saraf yang lebih luas mempunyai keupayaan generalisasi yang baik. Ini kerana rangkaian yang lebih luas mempunyai lebih banyak sub-rangkaian dan lebih berkemungkinan menghasilkan keselarasan kecerunan daripada rangkaian yang lebih kecil, menghasilkan generalisasi yang lebih baik. Dalam erti kata lain, keturunan kecerunan ialah pemilih ciri yang mengutamakan kecerunan generalisasi (kepaduan), dan rangkaian yang lebih luas mungkin mempunyai ciri yang lebih baik hanya kerana mereka mempunyai lebih banyak ciri.
- Kertas asal: Generalisasi dan lebar Neyshabur et al [2018b] mendapati bahawa rangkaian yang lebih luas dapat menjelaskan perkara ini secara intuitif, rangkaian yang lebih luas pada tahap tertentu. maka sub-rangkaian dengan koheren maksimum dalam rangkaian yang lebih luas mungkin lebih koheren daripada rakan sejawatannya dalam rangkaian yang lebih nipis, dan oleh itu menggeneralisasikan dengan lebih baik, kerana—seperti yang dibincangkan dalam Bahagian 10—keturunan kecerunan ialah pemilih ciri yang mengutamakan. ciri generalisasi (koheren), rangkaian yang lebih luas berkemungkinan mempunyai ciri yang lebih baik hanya kerana mereka mempunyai lebih banyak ciri Dalam hubungan ini, lihat juga Hipotesis Tiket Loteri [Frankle dan Carbin, 2018]
- Pautan kertas :https. ://github.com/aialgorithm/Blog
Tetapi secara peribadi, saya rasa ia masih perlu membezakan lebar lapisan input rangkaian/lapisan tersembunyi. Terutama untuk lapisan input tugas perlombongan data, kerana ciri input biasanya direka secara manual, anda perlu mempertimbangkan pemilihan ciri (iaitu, mengurangkan lebar lapisan input Jika tidak, bunyi ciri input secara langsung akan mengganggu koheren kecerunan). .
2.2 Generalisasi Rangkaian Neural Dalam
Semakin dalam rangkaian, fenomena koheren kecerunan dikuatkan dan mempunyai keupayaan generalisasi yang lebih baik.

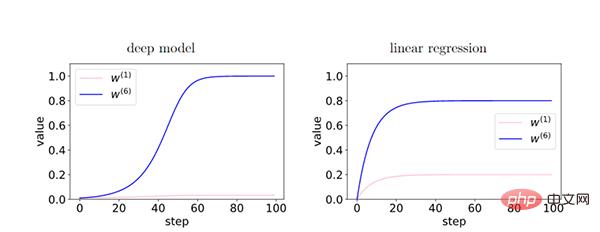
Dalam model dalam, memandangkan maklum balas antara lapisan menguatkan kecerunan koheren, terdapat ciri-ciri kecerunan koheren (W6) dan ciri-ciri kecerunan tidak koheren ( Perbezaan relatif antara W1) dikuatkan secara eksponen semasa latihan. Ini menjadikan rangkaian yang lebih dalam memilih kecerunan yang koheren, menghasilkan keupayaan generalisasi yang lebih baik.
2.3 Berhenti awal
Dengan berhenti awal, kita boleh mengurangkan pengaruh kecerunan tidak koheren yang berlebihan dan meningkatkan generalisasi.
Semasa latihan, beberapa sampel mudah dipasang lebih awal daripada sampel lain (sampel keras). Pada peringkat awal latihan, kecerunan korelasi sampel mudah ini mendominasi dan mudah untuk dimuatkan. Pada peringkat akhir latihan, kecerunan tidak koheren sampel sukar mendominasi kecerunan purata g(wt), mengakibatkan keupayaan generalisasi yang lemah Pada masa ini, adalah perlu untuk berhenti lebih awal.

- (Nota: Sampel mudah ialah sampel yang mempunyai banyak kecerunan yang sama dalam set data. Atas sebab ini, kebanyakan kecerunan memberi manfaat kepadanya. , penumpuan juga lebih cepat. Tambahan pula, eksperimen yang teliti menunjukkan bahawa keturunan kecerunan stokastik tidak semestinya membawa kepada generalisasi yang lebih baik, tetapi ini tidak menolak kemungkinan bahawa kecerunan stokastik lebih berkemungkinan melompat keluar dari minima tempatan, memainkan peranan dalam regularisasi, dsb.
Berdasarkan teori kami, kadar pembelajaran terhingga dan stokastik kumpulan mini tidak diperlukan untuk generalisasi
Kami percaya bahawa kadar pembelajaran yang lebih rendah mungkin tidak mengurangkan ralat generalisasi , kerana kadar pembelajaran yang lebih rendah bermakna lebih banyak lelaran (bertentangan dengan berhenti awal).- Dengan mengandaikan kadar pembelajaran yang cukup kecil, semasa latihan berlangsung, jurang generalisasi tidak boleh berkurangan Ini berikutan daripada analisis kestabilan berulang latihan: dengan 40 langkah lagi, kestabilan hanya boleh merosot dalam suasana praktikal, ia akan menunjukkan had teori yang menarik
- Tambah L2, L1 regularization pada fungsi objektif, dan pengiraan kecerunan yang sepadan , Kecerunan yang perlu ditambah pada sebutan biasa L1 ialah tanda(w), dan kecerunan L2 ialah w. Mengambil penyelarasan L2 sebagai contoh, formula kemas kini kecerunan W(i+1) yang sepadan ialah: Gambar
Kita boleh menganggap "penyaturan L2 (pereputan berat)" sebagai A "daya latar belakang" yang boleh menolak setiap parameter hampir kepada nilai sifar bebas data (L1 dengan mudah boleh mendapatkan penyelesaian yang jarang, dan L2 dengan mudah boleh mendapatkan penyelesaian yang lancar menghampiri 0) untuk menghapuskan pengaruh dalam arah kecerunan yang lemah. Hanya dalam kes arah kecerunan yang koheren, parameter boleh dipisahkan secara relatif daripada "daya latar belakang" dan kemas kini kecerunan boleh diselesaikan berdasarkan data.
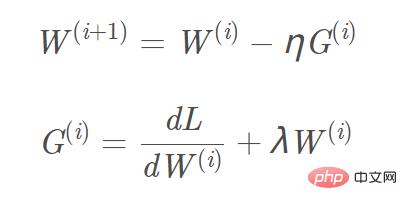
2.6 Algoritma Turun Kecerunan Lanjutan
 Momentum, Adam dan algoritma keturunan kecerunan lain
Momentum, Adam dan algoritma keturunan kecerunan lain
- Sekat penurunan kecerunan dalam arah kecerunan lemah
Ringkasan
Beberapa ayat di akhir artikel Jika anda berminat dengan teori pembelajaran mendalam, anda boleh membaca penyelidikan berkaitan yang dinyatakan dalam kertas. 
Atas ialah kandungan terperinci Sebuah artikel membincangkan secara ringkas keupayaan generalisasi pembelajaran mendalam. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1374
1374
 52
52
 Kaedah dan langkah untuk menggunakan BERT untuk analisis sentimen dalam Python
Jan 22, 2024 pm 04:24 PM
Kaedah dan langkah untuk menggunakan BERT untuk analisis sentimen dalam Python
Jan 22, 2024 pm 04:24 PM
BERT ialah model bahasa pembelajaran mendalam pra-latihan yang dicadangkan oleh Google pada 2018. Nama penuh ialah BidirectionalEncoderRepresentationsfromTransformers, yang berdasarkan seni bina Transformer dan mempunyai ciri pengekodan dwiarah. Berbanding dengan model pengekodan sehala tradisional, BERT boleh mempertimbangkan maklumat kontekstual pada masa yang sama semasa memproses teks, jadi ia berfungsi dengan baik dalam tugas pemprosesan bahasa semula jadi. Dwiarahnya membolehkan BERT memahami dengan lebih baik hubungan semantik dalam ayat, dengan itu meningkatkan keupayaan ekspresif model. Melalui kaedah pra-latihan dan penalaan halus, BERT boleh digunakan untuk pelbagai tugas pemprosesan bahasa semula jadi, seperti analisis sentimen, penamaan.
 YOLO adalah abadi! YOLOv9 dikeluarkan: prestasi dan kelajuan SOTA~
Feb 26, 2024 am 11:31 AM
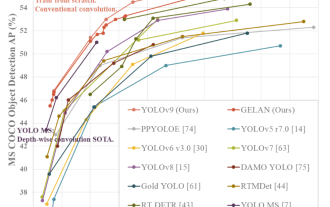
YOLO adalah abadi! YOLOv9 dikeluarkan: prestasi dan kelajuan SOTA~
Feb 26, 2024 am 11:31 AM
Kaedah pembelajaran mendalam hari ini memberi tumpuan kepada mereka bentuk fungsi objektif yang paling sesuai supaya keputusan ramalan model paling hampir dengan situasi sebenar. Pada masa yang sama, seni bina yang sesuai mesti direka bentuk untuk mendapatkan maklumat yang mencukupi untuk ramalan. Kaedah sedia ada mengabaikan fakta bahawa apabila data input mengalami pengekstrakan ciri lapisan demi lapisan dan transformasi spatial, sejumlah besar maklumat akan hilang. Artikel ini akan menyelidiki isu penting apabila menghantar data melalui rangkaian dalam, iaitu kesesakan maklumat dan fungsi boleh balik. Berdasarkan ini, konsep maklumat kecerunan boleh atur cara (PGI) dicadangkan untuk menghadapi pelbagai perubahan yang diperlukan oleh rangkaian dalam untuk mencapai pelbagai objektif. PGI boleh menyediakan maklumat input lengkap untuk tugas sasaran untuk mengira fungsi objektif, dengan itu mendapatkan maklumat kecerunan yang boleh dipercayai untuk mengemas kini berat rangkaian. Di samping itu, rangka kerja rangkaian ringan baharu direka bentuk
 Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Ditulis sebelum ini, hari ini kita membincangkan bagaimana teknologi pembelajaran mendalam boleh meningkatkan prestasi SLAM berasaskan penglihatan (penyetempatan dan pemetaan serentak) dalam persekitaran yang kompleks. Dengan menggabungkan kaedah pengekstrakan ciri dalam dan pemadanan kedalaman, di sini kami memperkenalkan sistem SLAM visual hibrid serba boleh yang direka untuk meningkatkan penyesuaian dalam senario yang mencabar seperti keadaan cahaya malap, pencahayaan dinamik, kawasan bertekstur lemah dan seks yang teruk. Sistem kami menyokong berbilang mod, termasuk konfigurasi monokular, stereo, monokular-inersia dan stereo-inersia lanjutan. Selain itu, ia juga menganalisis cara menggabungkan SLAM visual dengan kaedah pembelajaran mendalam untuk memberi inspirasi kepada penyelidikan lain. Melalui percubaan yang meluas pada set data awam dan data sampel sendiri, kami menunjukkan keunggulan SL-SLAM dari segi ketepatan kedudukan dan keteguhan penjejakan.
 Pembenaman ruang terpendam: penjelasan dan demonstrasi
Jan 22, 2024 pm 05:30 PM
Pembenaman ruang terpendam: penjelasan dan demonstrasi
Jan 22, 2024 pm 05:30 PM
Pembenaman Ruang Terpendam (LatentSpaceEmbedding) ialah proses memetakan data berdimensi tinggi kepada ruang berdimensi rendah. Dalam bidang pembelajaran mesin dan pembelajaran mendalam, pembenaman ruang terpendam biasanya merupakan model rangkaian saraf yang memetakan data input berdimensi tinggi ke dalam set perwakilan vektor berdimensi rendah ini sering dipanggil "vektor terpendam" atau "terpendam pengekodan". Tujuan pembenaman ruang terpendam adalah untuk menangkap ciri penting dalam data dan mewakilinya ke dalam bentuk yang lebih ringkas dan mudah difahami. Melalui pembenaman ruang terpendam, kami boleh melakukan operasi seperti memvisualisasikan, mengelaskan dan mengelompokkan data dalam ruang dimensi rendah untuk memahami dan menggunakan data dengan lebih baik. Pembenaman ruang terpendam mempunyai aplikasi yang luas dalam banyak bidang, seperti penjanaan imej, pengekstrakan ciri, pengurangan dimensi, dsb. Pembenaman ruang terpendam adalah yang utama
 Fahami dalam satu artikel: kaitan dan perbezaan antara AI, pembelajaran mesin dan pembelajaran mendalam
Mar 02, 2024 am 11:19 AM
Fahami dalam satu artikel: kaitan dan perbezaan antara AI, pembelajaran mesin dan pembelajaran mendalam
Mar 02, 2024 am 11:19 AM
Dalam gelombang perubahan teknologi yang pesat hari ini, Kecerdasan Buatan (AI), Pembelajaran Mesin (ML) dan Pembelajaran Dalam (DL) adalah seperti bintang terang, menerajui gelombang baharu teknologi maklumat. Ketiga-tiga perkataan ini sering muncul dalam pelbagai perbincangan dan aplikasi praktikal yang canggih, tetapi bagi kebanyakan peneroka yang baru dalam bidang ini, makna khusus dan hubungan dalaman mereka mungkin masih diselubungi misteri. Jadi mari kita lihat gambar ini dahulu. Dapat dilihat bahawa terdapat korelasi rapat dan hubungan progresif antara pembelajaran mendalam, pembelajaran mesin dan kecerdasan buatan. Pembelajaran mendalam ialah bidang khusus pembelajaran mesin dan pembelajaran mesin
 Super kuat! 10 algoritma pembelajaran mendalam teratas!
Mar 15, 2024 pm 03:46 PM
Super kuat! 10 algoritma pembelajaran mendalam teratas!
Mar 15, 2024 pm 03:46 PM
Hampir 20 tahun telah berlalu sejak konsep pembelajaran mendalam dicadangkan pada tahun 2006. Pembelajaran mendalam, sebagai revolusi dalam bidang kecerdasan buatan, telah melahirkan banyak algoritma yang berpengaruh. Jadi, pada pendapat anda, apakah 10 algoritma teratas untuk pembelajaran mendalam? Berikut adalah algoritma teratas untuk pembelajaran mendalam pada pendapat saya Mereka semua menduduki kedudukan penting dari segi inovasi, nilai aplikasi dan pengaruh. 1. Latar belakang rangkaian saraf dalam (DNN): Rangkaian saraf dalam (DNN), juga dipanggil perceptron berbilang lapisan, adalah algoritma pembelajaran mendalam yang paling biasa Apabila ia mula-mula dicipta, ia dipersoalkan kerana kesesakan kuasa pengkomputeran tahun, kuasa pengkomputeran, Kejayaan datang dengan letupan data. DNN ialah model rangkaian saraf yang mengandungi berbilang lapisan tersembunyi. Dalam model ini, setiap lapisan menghantar input ke lapisan seterusnya dan
 1.3ms mengambil masa 1.3ms! Seni bina rangkaian neural mudah alih sumber terbuka terbaru Tsinghua RepViT
Mar 11, 2024 pm 12:07 PM
1.3ms mengambil masa 1.3ms! Seni bina rangkaian neural mudah alih sumber terbuka terbaru Tsinghua RepViT
Mar 11, 2024 pm 12:07 PM
Alamat kertas: https://arxiv.org/abs/2307.09283 Alamat kod: https://github.com/THU-MIG/RepViTRepViT berprestasi baik dalam seni bina ViT mudah alih dan menunjukkan kelebihan yang ketara. Seterusnya, kami meneroka sumbangan kajian ini. Disebutkan dalam artikel bahawa ViT ringan biasanya berprestasi lebih baik daripada CNN ringan pada tugas visual, terutamanya disebabkan oleh modul perhatian diri berbilang kepala (MSHA) mereka yang membolehkan model mempelajari perwakilan global. Walau bagaimanapun, perbezaan seni bina antara ViT ringan dan CNN ringan belum dikaji sepenuhnya. Dalam kajian ini, penulis menyepadukan ViT ringan ke dalam yang berkesan
 Cara menggunakan model hibrid CNN dan Transformer untuk meningkatkan prestasi
Jan 24, 2024 am 10:33 AM
Cara menggunakan model hibrid CNN dan Transformer untuk meningkatkan prestasi
Jan 24, 2024 am 10:33 AM
Rangkaian Neural Konvolusi (CNN) dan Transformer ialah dua model pembelajaran mendalam berbeza yang telah menunjukkan prestasi cemerlang pada tugasan yang berbeza. CNN digunakan terutamanya untuk tugas penglihatan komputer seperti klasifikasi imej, pengesanan sasaran dan pembahagian imej. Ia mengekstrak ciri tempatan pada imej melalui operasi lilitan, dan melakukan pengurangan dimensi ciri dan invarian ruang melalui operasi pengumpulan. Sebaliknya, Transformer digunakan terutamanya untuk tugas pemprosesan bahasa semula jadi (NLP) seperti terjemahan mesin, klasifikasi teks dan pengecaman pertuturan. Ia menggunakan mekanisme perhatian kendiri untuk memodelkan kebergantungan dalam jujukan, mengelakkan pengiraan berjujukan dalam rangkaian saraf berulang tradisional. Walaupun kedua-dua model ini digunakan untuk tugasan yang berbeza, ia mempunyai persamaan dalam pemodelan jujukan, jadi