Teori graf sebenarnya tidak sukar untuk dimulakan
Bagi pembangun yang mempunyai pengalaman pengaturcaraan selama bertahun-tahun, konsep graf bukanlah sesuatu yang asing. Banyak syarikat terkemuka menguji pemahaman teori graf semasa temuduga teknikal. Malah, pembangun tidak perlu menangani isu lanjutan untuk memanfaatkan konsep ini. Untuk memahami perkara ini, kita boleh menyemak dahulu sebab graf ialah struktur data yang popular dan cara melaksanakannya dalam kod.
Model Perhubungan
Tidak kira pengalaman pengekodan, pembangun harus mempunyai sedikit pemahaman tentang jenis data tatasusunan dan kamus. Koleksi ini ialah konsep standard yang digunakan dalam kebanyakan bahasa dan berfungsi dengan baik apabila memaparkan kandungan berasaskan senarai:

Kebanyakan masa senarai itu diambil daripada pangkalan data atau berasaskan on REST Penyelesaian sempurna untuk memaparkan maklumat dalam pertanyaan. Walau bagaimanapun, kadangkala senarai perlu menyediakan rekod yang mempunyai konteks yang saling berkaitan. Pada ketika ini, lebih mudah untuk menyusun data ke dalam carta.
Dengan gambar rajah, matlamat utama bukanlah untuk menyenaraikan maklumat (walaupun ini boleh dilakukan), tetapi untuk menentukan hubungan antara objek. Mengapakah ia berguna untuk menentukan hubungan antara objek? Mari kita lihat contoh berikut.

Graf tidak berarah dengan dua bucu dan satu tepi
(1) Aplikasi peta:
Jika ditanya dalam temu bual teknikal, bagaimanakah anda akan menyusun data untuk mencipta semula perkhidmatan pemetaan (seperti Apple atau Peta Google)? Selain menyediakan senarai semua jalan yang diketahui dalam pangkalan data, model yang anda cipta perlu menentukan cara terbaik untuk sampai ke destinasi anda berdasarkan faktor seperti masa dalam sehari, lalu lintas dan jalan sehala. Untuk menjadikan jumlah data yang besar ini berfungsi, anda perlu mengetahui hubungan antara jalan dan semua jalan lain dalam model.
(2) Media sosial :
Nilai sesuatu media sosial biasanya diukur dengan bilangan pengguna yang mengikuti atau mengikuti pengguna. Platform web seperti Twitter menarik sejumlah besar pengguna dengan membenarkan mereka berhubung dengan sesiapa sahaja dan menerima kemas kini terkini mereka.
Model LinkedIn lebih terperinci kerana pengguna tidak boleh menambahkan seseorang pada rangkaian pengguna tersebut melainkan penerima menerima permintaan sambungan pengguna. Dalam kes ini, sambungan LinkedIn mewakili hubungan dua hala. Sepanjang baris ini, pengguna juga boleh mencari rangkaian mereka untuk melihat sama ada sesiapa dikaitkan dengan peluang pekerjaan yang mereka inginkan. Dalam konteks ini, "rangkaian" mungkin bermaksud sambungan langsung atau tidak langsung. Model berkuasa sedemikian bukan hanya berdasarkan senarai ringkas, ia mengandungi kecerdasan untuk menentukan bagaimana semua profil berkaitan.
Komponen Grafik
Sekarang kita memahami cara graf digunakan dalam aplikasi harian, mari perkenalkan komponen graf.
Nod dalam graf dipanggil bucu. Walaupun graf boleh dibina sebagai bucu tunggal, model yang mengandungi berbilang bucu lebih baik mewakili aplikasi dunia sebenar.
Objek dalam graf adalah berkaitan antara satu sama lain melalui sambungan yang dipanggil tepi.
Bergantung pada keperluan anda, bucu boleh disambungkan kepada satu atau lebih objek melalui tepi, atau anda boleh mencipta bucu tanpa tepi.
Akhir sekali, tidak seperti struktur standard lain seperti tindanan atau baris gilir, graf biasanya tidak mempunyai titik mula atau akhir yang ditetapkan. Berikut ialah beberapa contoh konfigurasi graf:

Graf tidak berarah dengan dua bucu dan satu tepi
Graf tidak berarah dengan dua bucu dan satu tepi
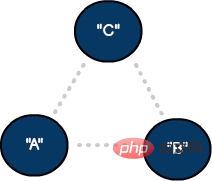
Graf tidak berarah dengan Tidak berarah graf dengan dua bucu dan satu tepi
Berarah lwn. Tidak Berarah
Dalam graf tidak berarah, hubungan antara bucu sumber dan destinasi adalah sama. Model ini mewakili sambungan dua hala—serupa dengan jalan dua hala dalam aplikasi pemetaan.
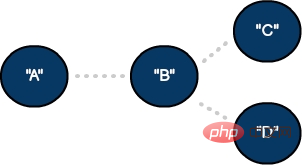
Untuk menentukan sambungan sehala, kami boleh mengemas kini model kepada graf terarah menggunakan garisan dan anak panah:
Tiga bucu dan tiga Graf Tepi Berarah
Tahap Kesambungan
Kadangkala, kita perlu mewakili darjah ketersambungan antara bucu dalam graf. Teknik ini berfungsi dengan baik apabila mengira jarak, masa atau keterukan antara nod. Berat biasanya dikaitkan dengan tepi dan merupakan pembolehubah perbandingan yang digunakan untuk penjejakan. .
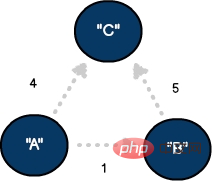
Graf terarah dengan tiga bucu dan tiga tepi, di mana tepi ditimbang
Bucu Graf
Dengan pemahaman asas teori graf, mari lihat cara untuk meniru model ini dalam kod. Di bawah ini kami mencipta bucu yang menyokong objek generik tersuai (T). Pembolehubah nilai t mewakili data yang dipegang oleh jenis itu, termasuk rentetan tunggal, int atau jenis tersuai (contohnya, nama jalan atau profil media sosial).
Selain itu, pastikan jenis kami mematuhi protokol Equatable (Swift) yang popular. Ini membolehkan kami membandingkan kejadian puncak tertentu untuk kesaksamaan apabila diperlukan.
public class Vertex <t> : Equatable {<br><br>var tvalue: T?<br>var neighbors = Array<edge>>()<br>let uuid = UUID()<br><br>public init(with name: T) {<br>self.tvalue = name<br>}<br><br>//equatable conformance<br>public static func == (lhs: Vertex, rhs: Vertex) -> Bool {<br> return lhs.uuid == rhs.uuid<br>}<br>}</edge></t>
Senarai bersebelahan
Senarai bersebelahan mewakili sambungan ke bucu lain. Seperti yang dinyatakan sebelum ini, setiap bucu boleh disambungkan kepada satu atau lebih bucu bersebelahan. Senarai perhubungan ini kadangkala dipanggil "senarai bersebelahan" dan boleh digunakan untuk menyelesaikan banyak masalah lanjutan.
var neighbors = Array<edge>>()</edge>
Tepi Graf
Apabila mencipta bucu, kami menambah sifat bersebelahan untuk menyimpan tatasusunan jenis tepi tersuai. Tepi seterusnya memberikan rujukan untuk bucu bersebelahan seterusnya dan potensi berat tepinya.
public class Edge <t> {<br><br>var neighbor: Vertex<t><br>var weight: Int<br><br>init() {<br> weight = 0<br> self.neighbor = Vertex<t>()<br>}<br>}</t></t></t>Membina kanvas
Dengan objek bucu dan tepi di tangan kita kini boleh menambahnya pada struktur storan pusat yang kita panggil kanvas graf . Walaupun kanvas kami secara teknikal adalah tatasusunan, matlamat kami adalah untuk menggambarkan koleksi sebagai satu set perhubungan. Dengan fungsi addVertex kita boleh menambah satu puncak generik pada kanvas, manakala kaedah addEdge menyediakan maklumat rujukan yang diperlukan untuk tepi.
Akhir sekali, kod kami menganggap bahawa graf diarahkan, kerana tepi (hanya) ditambahkan pada senarai bersebelahan bucu sumber.
public class Graph <t> {<br><br>var canvas: Array<vertex>><br><br> public init() {<br> canvas = Array<vertex>()<br>}<br><br>//add vertex to graph canvas<br>public func addVertex(element: Vertex<t>) {<br> canvas.append(element)<br>}<br>/add edge<br>public func addEdge(source: Vertex<t>, neighbor: Vertex<t>, weight: Int) {<br><br> //create a new edge<br> let newEdge = Edge<t>()<br><br> //connect source vertex to neighboring edge<br> newEdge.neighbor = neighbor<br> newEdge.weight = weight<br><br> source.neighbors.append(newEdge)<br>}<br>}</t></t></t></t></vertex></vertex></t>Ringkasnya, kami memperkenalkan anda kepada graf dan melihat cara ia boleh digunakan untuk mewakili perhubungan antara objek Kami juga menyemak beberapa cara untuk mengkonfigurasi graf dan komponen yang digunakan untuk menerangkan model yang berbeza.
Setelah model ditakrifkan, kami meletakkan asas untuk ciri yang lebih maju, termasuk navigasi graf dan algoritma traversal seperti carian luas-dahulu.
Pengenalan Penterjemah
Kang Shaojing, editor komuniti 51CTO, kini terlibat dalam industri komunikasi, bekerja dalam jawatan pembangunan pemandu peringkat rendah Dia telah mempelajari struktur data, Python, dan kini berminat dalam sistem pengendalian, pangkalan data dan bidang lain yang berkaitan.
Tajuk asal: Panduan lengkap pemula untuk teori graf, pengarang: Wayne Bishop
Pautan:
https://stackoverflow.blog/2022/05/26/the -panduan-pemula-lengkap-ke-teori-graf/
Atas ialah kandungan terperinci Teori graf sebenarnya tidak sukar untuk dimulakan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1379
1379
 52
52
 Saya cuba pengekodan getaran dengan kursor AI dan ia menakjubkan!
Mar 20, 2025 pm 03:34 PM
Saya cuba pengekodan getaran dengan kursor AI dan ia menakjubkan!
Mar 20, 2025 pm 03:34 PM
Pengekodan Vibe membentuk semula dunia pembangunan perisian dengan membiarkan kami membuat aplikasi menggunakan bahasa semulajadi dan bukannya kod yang tidak berkesudahan. Diilhamkan oleh penglihatan seperti Andrej Karpathy, pendekatan inovatif ini membolehkan Dev
 Top 5 Genai dilancarkan pada Februari 2025: GPT-4.5, Grok-3 & More!
Mar 22, 2025 am 10:58 AM
Top 5 Genai dilancarkan pada Februari 2025: GPT-4.5, Grok-3 & More!
Mar 22, 2025 am 10:58 AM
Februari 2025 telah menjadi satu lagi bulan yang berubah-ubah untuk AI generatif, membawa kita beberapa peningkatan model yang paling dinanti-nantikan dan ciri-ciri baru yang hebat. Dari Xai's Grok 3 dan Anthropic's Claude 3.7 Sonnet, ke Openai's G
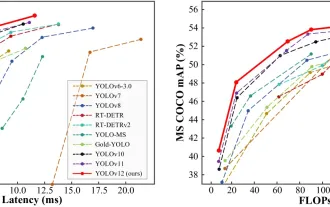 Bagaimana cara menggunakan Yolo V12 untuk pengesanan objek?
Mar 22, 2025 am 11:07 AM
Bagaimana cara menggunakan Yolo V12 untuk pengesanan objek?
Mar 22, 2025 am 11:07 AM
Yolo (anda hanya melihat sekali) telah menjadi kerangka pengesanan objek masa nyata yang terkemuka, dengan setiap lelaran bertambah baik pada versi sebelumnya. Versi terbaru Yolo V12 memperkenalkan kemajuan yang meningkatkan ketepatan
 Penjana Seni AI Terbaik (Percuma & amp; Dibayar) untuk projek kreatif
Apr 02, 2025 pm 06:10 PM
Penjana Seni AI Terbaik (Percuma & amp; Dibayar) untuk projek kreatif
Apr 02, 2025 pm 06:10 PM
Artikel ini mengkaji semula penjana seni AI atas, membincangkan ciri -ciri mereka, kesesuaian untuk projek kreatif, dan nilai. Ia menyerlahkan Midjourney sebagai nilai terbaik untuk profesional dan mengesyorkan Dall-E 2 untuk seni berkualiti tinggi dan disesuaikan.
 Adakah chatgpt 4 o tersedia?
Mar 28, 2025 pm 05:29 PM
Adakah chatgpt 4 o tersedia?
Mar 28, 2025 pm 05:29 PM
CHATGPT 4 kini tersedia dan digunakan secara meluas, menunjukkan penambahbaikan yang ketara dalam memahami konteks dan menjana tindak balas yang koheren berbanding dengan pendahulunya seperti ChATGPT 3.5. Perkembangan masa depan mungkin merangkumi lebih banyak Inter yang diperibadikan
 AI mana yang lebih baik daripada chatgpt?
Mar 18, 2025 pm 06:05 PM
AI mana yang lebih baik daripada chatgpt?
Mar 18, 2025 pm 06:05 PM
Artikel ini membincangkan model AI yang melampaui chatgpt, seperti Lamda, Llama, dan Grok, menonjolkan kelebihan mereka dalam ketepatan, pemahaman, dan kesan industri. (159 aksara)
 Cara Menggunakan Mistral OCR untuk Model RAG Seterusnya
Mar 21, 2025 am 11:11 AM
Cara Menggunakan Mistral OCR untuk Model RAG Seterusnya
Mar 21, 2025 am 11:11 AM
Mistral OCR: Merevolusi Generasi Pengambilan Pengambilan semula dengan Pemahaman Dokumen Multimodal Sistem Generasi Pengambilan Retrieval (RAG) mempunyai keupayaan AI yang ketara, membolehkan akses ke kedai data yang luas untuk mendapatkan respons yang lebih tepat
 Pembantu Menulis AI Teratas untuk Meningkatkan Penciptaan Kandungan Anda
Apr 02, 2025 pm 06:11 PM
Pembantu Menulis AI Teratas untuk Meningkatkan Penciptaan Kandungan Anda
Apr 02, 2025 pm 06:11 PM
Artikel ini membincangkan pembantu penulisan AI terkemuka seperti Grammarly, Jasper, Copy.ai, WriteSonic, dan Rytr, yang memberi tumpuan kepada ciri -ciri unik mereka untuk penciptaan kandungan. Ia berpendapat bahawa Jasper cemerlang dalam pengoptimuman SEO, sementara alat AI membantu mengekalkan nada terdiri




