 pembangunan bahagian belakang
pembangunan bahagian belakang
 Tutorial Python
Tutorial Python
 Menggunakan vektorisasi untuk menggantikan gelung dalam python
Menggunakan vektorisasi untuk menggantikan gelung dalam python
Menggunakan vektorisasi untuk menggantikan gelung dalam python
Semua bahasa pengaturcaraan tidak dapat dipisahkan daripada gelung. Jadi, secara lalai, kami mula melaksanakan gelung apabila terdapat operasi berulang. Tetapi apabila kita berhadapan dengan sejumlah besar lelaran (berjuta-juta/berbilion baris), menggunakan gelung adalah satu jenayah. Anda mungkin terperangkap selama beberapa jam, hanya untuk menyedari kemudian bahawa ia tidak berfungsi. Di sinilah pelaksanaan vektorisasi dalam python menjadi sangat kritikal.
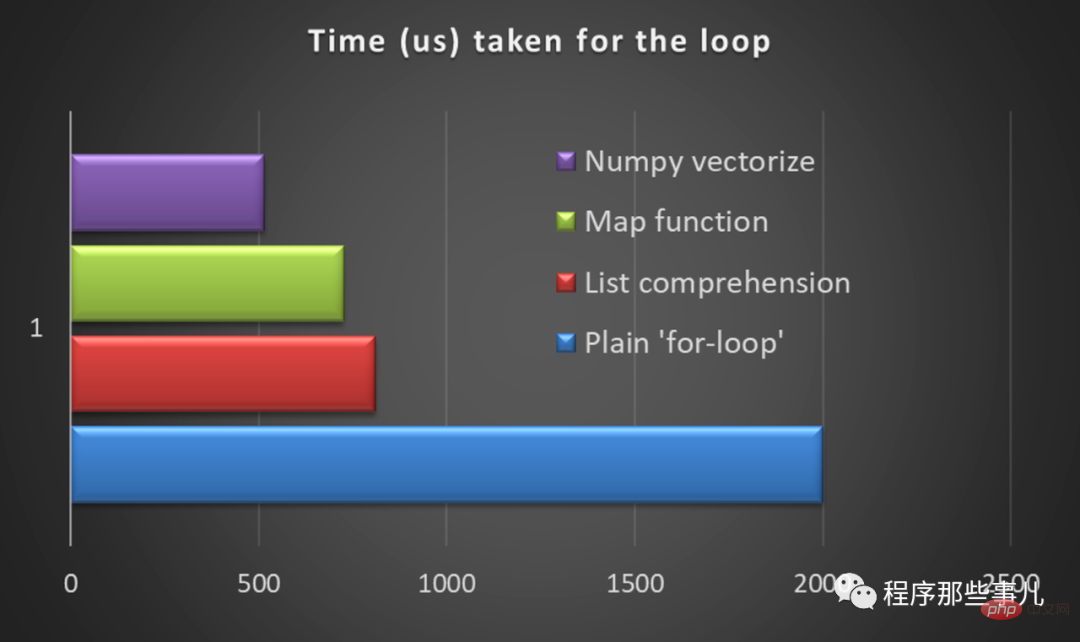
Apakah itu vektorisasi?
Vektorisasi ialah teknik untuk melaksanakan operasi tatasusunan (NumPy) pada set data. Di sebalik tabir, ia menggunakan operasi kepada semua elemen tatasusunan atau siri sekali gus (tidak seperti gelung "untuk" yang mengendalikan satu baris pada satu masa).
Seterusnya kami menggunakan beberapa kes penggunaan untuk menunjukkan apa itu vektorisasi.
Jumlah nombor
##使用循环
import time
start = time.time()
# iterative sum
total = 0
# iterating through 1.5 Million numbers
for item in range(0, 1500000):
total = total + item
print('sum is:' + str(total))
end = time.time()
print(end - start)
#1124999250000
#0.14 Seconds## 使用矢量化 import numpy as np start = time.time() # vectorized sum - using numpy for vectorization # np.arange create the sequence of numbers from 0 to 1499999 print(np.sum(np.arange(1500000))) end = time.time() print(end - start) ##1124999250000 ##0.008 Seconds
Masa pelaksanaan vektorisasi dikurangkan berbanding lelaran menggunakan fungsi julat Kira-kira 18 kali. Perbezaan ini menjadi lebih ketara apabila menggunakan Pandas DataFrame.
Operasi Matematik
Dalam sains data, apabila bekerja dengan Pandas DataFrame, pembangun menggunakan gelung untuk mencipta lajur terbitan baharu melalui operasi matematik.
Dalam contoh di bawah, kita dapat melihat betapa mudahnya untuk menggantikan gelung dengan vektorisasi untuk kes penggunaan sedemikian.
DataFrame ialah data jadual dalam bentuk baris dan lajur.
Kami mencipta DataFrame panda dengan 5 juta baris dan 4 lajur yang diisi dengan nilai rawak antara 0 dan 50.

import numpy as np import pandas as pd df = pd.DataFrame(np.random.randint( 0 , 50 , size=( 5000000 , 4 )), columns=( 'a' , 'b' , 'c' , 'd ' )) df.shape # (5000000, 5) df.head()
Buat "nisbah" lajur baharu untuk mencari nisbah lajur "d" dan "c".
## 循环遍历 import time start = time.time() # 使用 iterrows 遍历 DataFrame for idx, row in df.iterrows(): # 创建一个新列 df.at[idx, 'ratio' ] = 100 * (row[ "d" ] / row[ "c" ]) end = time.time() print (end - start) ### 109 秒
## 使用矢量化 start = time.time() df[ "ratio" ] = 100 * (df[ "d" ] / df[ "c" ]) end = time.time() print (end - start) ### 0.12 秒
Kita boleh melihat peningkatan yang ketara dengan DataFrame, dengan operasi vektor mengambil masa hampir 1000 kali lebih pantas berbanding gelung dalam Python.
Pernyataan If-else
Kami telah melaksanakan banyak operasi yang memerlukan kami menggunakan logik jenis "If-else". Kita boleh dengan mudah menggantikan logik ini dengan operasi vektor dalam python.
Mari kita lihat contoh berikut untuk memahaminya dengan lebih baik (kita akan menggunakan DataFrame yang kita buat dalam use case 2):
Bayangkan kita ingin menggunakan lajur "a" sedia ada Buat a lajur baharu "e" dengan beberapa syarat pada
## 使用循环 import time start = time.time() # 使用 iterrows 遍历 DataFrame for idx, row in df.iterrows(): if row.a == 0 : df.at[idx, 'e' ] = row.d elif ( row.a <= 25 ) & (row.a > 0 ): df.at[idx, 'e' ] = (row.b)-(row.c) else : df.at[idx, 'e' ] = row.b + row.c end = time.time() print (end - start) ### 耗时:166 秒
## 矢量化 start = time.time() df[ 'e' ] = df[ 'b' ] + df[ 'c' ] df.loc[df[ 'a' ] <= 25 , 'e' ] = df [ 'b' ] -df[ 'c' ] df.loc[df[ 'a' ]== 0 , 'e' ] = df[ 'd' ]end = time.time() 打印(结束 - 开始) ## 0.29007707595825195 秒
Operasi vektor mengambil masa 600 kali lebih pantas berbanding gelung ular sawa menggunakan pernyataan if-else.
Menyelesaikan Pembelajaran Mesin/Rangkaian Pembelajaran Mendalam
Pembelajaran mendalam memerlukan kita menyelesaikan berbilang persamaan kompleks dan terdapat berjuta-juta dan berjuta-juta persamaan untuk diselesaikan Masalah berbilion baris. Menjalankan gelung untuk menyelesaikan persamaan ini dalam Python adalah sangat perlahan dan vektorisasi adalah penyelesaian terbaik.
Sebagai contoh, untuk mengira nilai-y untuk berjuta-juta baris dalam persamaan regresi linear berbilang berikut:
Kita boleh vektorkan bukannya gelung .
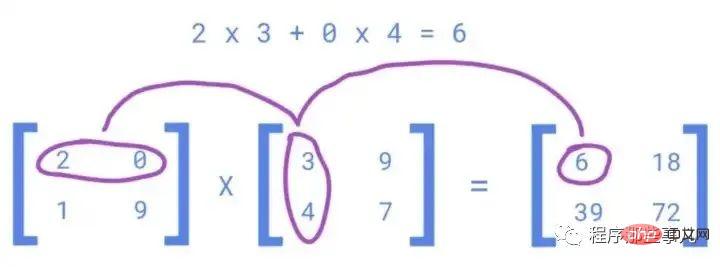
Nilai m1, m2, m3... ditentukan dengan menyelesaikan persamaan di atas menggunakan berjuta-juta nilai yang sepadan dengan x1, x2, x3.. .
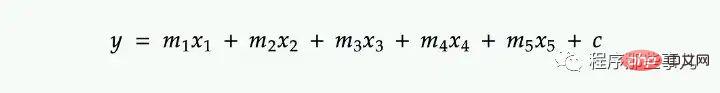
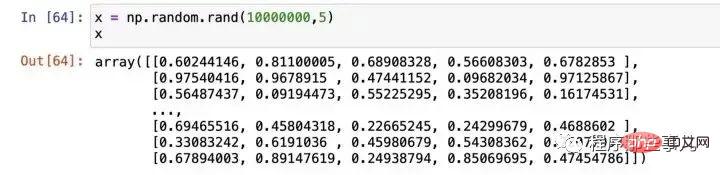
import numpy as np # 设置 m 的初始值 m = np.random.rand( 1 , 5 ) # 500 万行的输入值 x = np.random.rand( 5000000 , 5 )
## 使用循环
import numpy as np
m = np.random.rand(1,5)
x = np.random.rand(5000000,5)
total = 0
tic = time.process_time()
for i in range(0,5000000):
total = 0
for j in range(0,5):
total = total + x[i][j]*m[0][j]
zer[i] = total
toc = time.process_time()
print ("Computation time = "+ str ((toc - tic)) + "seconds" )
####计算时间 = 27.02 秒## 矢量化 tic = time.process_time() #dot product np.dot(x,mT) toc = time.process_time() print ( "计算时间 = " + str ((toc - tic)) + "seconds" ) ####计算时间 = 0.107 秒
np.dot melaksanakan pendaraban matriks vektor di bahagian belakang. Ia adalah 165 kali lebih pantas berbanding gelung dalam Python.
Kesimpulan
Vektorisasi dalam python adalah sangat pantas dan harus diutamakan berbanding gelung apabila kita berurusan dengan set data yang sangat besar.

Apabila anda mula melaksanakannya dari semasa ke semasa, anda akan terbiasa berfikir mengikut baris kod vektor.
Atas ialah kandungan terperinci Menggunakan vektorisasi untuk menggantikan gelung dalam python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Kuasai kekunci pintasan gantian PyCharm dalam masa 5 minit dan tingkatkan kelajuan pengaturcaraan anda dengan mudah!
Feb 22, 2024 am 10:57 AM
Kuasai kekunci pintasan gantian PyCharm dalam masa 5 minit dan tingkatkan kelajuan pengaturcaraan anda dengan mudah!
Feb 22, 2024 am 10:57 AM
PyCharm ialah persekitaran pembangunan bersepadu Python yang biasa digunakan dengan fungsi yang kaya dan kekunci pintasan yang boleh membantu pembangun meningkatkan kecekapan pengaturcaraan. Dalam proses pengaturcaraan harian, menguasai kemahiran penggantian kunci pintasan PyCharm boleh membantu pembangun menyelesaikan tugas dengan lebih cepat. Artikel ini akan memperkenalkan anda kepada beberapa kekunci pintasan gantian yang biasa digunakan dalam PyCharm untuk membantu anda meningkatkan kelajuan pengaturcaraan anda dengan mudah. 1. Penggantian Ctrl+R Dalam PyCharm, anda boleh menggunakan kekunci pintasan Ctrl+R untuk melakukan operasi penggantian.
 Panduan Pemula PyCharm: Analisis Komprehensif Fungsi Penggantian
Feb 25, 2024 am 11:15 AM
Panduan Pemula PyCharm: Analisis Komprehensif Fungsi Penggantian
Feb 25, 2024 am 11:15 AM
PyCharm ialah persekitaran pembangunan bersepadu Python yang berkuasa dengan fungsi dan alatan yang kaya yang boleh meningkatkan kecekapan pembangunan dengan ketara. Antaranya, fungsi penggantian merupakan salah satu fungsi yang kerap digunakan dalam proses pembangunan, yang boleh membantu pembangun mengubah suai kod dengan cepat dan meningkatkan kualiti kod. Artikel ini akan memperkenalkan fungsi gantian PyCharm secara terperinci, digabungkan dengan contoh kod khusus, untuk membantu orang baru menguasai dan menggunakan fungsi ini dengan lebih baik. Pengenalan kepada fungsi gantian Fungsi gantian PyCharm boleh membantu pembangun dengan cepat menggantikan teks yang ditentukan dalam kod
 Gantikan nama kelas elemen menggunakan jQuery
Feb 24, 2024 pm 11:03 PM
Gantikan nama kelas elemen menggunakan jQuery
Feb 24, 2024 pm 11:03 PM
jQuery ialah perpustakaan JavaScript klasik yang digunakan secara meluas dalam pembangunan web Ia memudahkan operasi seperti pengendalian acara, memanipulasi elemen DOM, dan melaksanakan animasi pada halaman web. Apabila menggunakan jQuery, anda sering menghadapi situasi di mana anda perlu menggantikan nama kelas elemen Artikel ini akan memperkenalkan beberapa kaedah praktikal dan contoh kod tertentu. 1. Gunakan kaedah removeClass() dan addClass() jQuery menyediakan kaedah removeClass() untuk pemadaman
 PyCharm menggantikan kekunci pintasan untuk menjadikan pengaturcaraan lebih mudah!
Feb 21, 2024 pm 12:03 PM
PyCharm menggantikan kekunci pintasan untuk menjadikan pengaturcaraan lebih mudah!
Feb 21, 2024 pm 12:03 PM
PyCharm ialah persekitaran pembangunan bersepadu yang popular di kalangan pengaturcara Ia menyediakan fungsi dan alatan yang berkuasa untuk menjadikan pengaturcaraan lebih cekap dan mudah. Dalam PyCharm, tetapan munasabah dan penggantian kekunci pintasan adalah salah satu kunci untuk meningkatkan kecekapan pengaturcaraan. Artikel ini akan memperkenalkan cara menggantikan kekunci pintasan dalam PyCharm untuk menjadikan pengaturcaraan lebih mudah. 1. Mengapakah kita harus menggantikan kekunci pintasan Dalam PyCharm, kekunci pintasan boleh membantu pengaturcara menyelesaikan pelbagai operasi dengan cepat dan meningkatkan kecekapan pengaturcaraan. Walau bagaimanapun, setiap orang mempunyai tabiat yang berbeza, dan sesetengah orang mungkin
 Bagaimana untuk menggantikan perkataan dalam Excel menggunakan Python?
Sep 16, 2023 pm 10:21 PM
Bagaimana untuk menggantikan perkataan dalam Excel menggunakan Python?
Sep 16, 2023 pm 10:21 PM
Dalam Python, kita boleh menggantikan satu perkataan dengan perkataan lain dalam Excel menggunakan perpustakaan Python pihak ketiga yang dipanggil openpyxl. Microsoft Excel ialah alat yang berguna untuk mengurus dan menganalisis data. Menggunakan Python, kami boleh mengautomasikan beberapa tugas pengurusan data Excel. Dalam artikel ini, kita akan belajar cara menggantikan perkataan dalam Excel menggunakan Python. Sebelum memasang openpyxl untuk menggantikan Word dalam Excel, kami perlu memasang perpustakaan openpyxl dalam sistem menggunakan pengurus pakej Python. Untuk memasang openpyxl, masukkan arahan berikut dalam terminal atau command prompt. Pipinst
 Ekspresi Lambda terkeluar daripada gelung
Feb 20, 2024 am 08:47 AM
Ekspresi Lambda terkeluar daripada gelung
Feb 20, 2024 am 08:47 AM
Ekspresi Lambda keluar dari gelung, contoh kod khusus diperlukan Dalam pengaturcaraan, struktur gelung ialah sintaks penting yang sering digunakan. Walau bagaimanapun, dalam keadaan tertentu, kita mungkin mahu keluar daripada keseluruhan gelung apabila keadaan tertentu dipenuhi dalam badan gelung, dan bukannya menamatkan lelaran gelung semasa. Pada masa ini, ciri-ciri ungkapan lambda boleh membantu kita mencapai matlamat untuk melompat keluar dari gelung. Ungkapan Lambda ialah cara untuk mengisytiharkan fungsi tanpa nama, yang boleh mentakrifkan logik fungsi mudah secara dalaman. Ia berbeza daripada pengisytiharan fungsi biasa,
 Mendedahkan rahsia cara cepat menggantikan kod dalam PyCharm
Feb 25, 2024 pm 11:21 PM
Mendedahkan rahsia cara cepat menggantikan kod dalam PyCharm
Feb 25, 2024 pm 11:21 PM
PyCharm ialah persekitaran pembangunan bersepadu Python yang disukai secara meluas oleh pembangun Ia menyediakan banyak cara untuk menggantikan kod dengan cepat, menjadikan proses pembangunan lebih cekap. Artikel ini akan mendedahkan beberapa kaedah yang biasa digunakan untuk menggantikan kod dalam PyCharm dengan cepat dan memberikan contoh kod khusus untuk membantu pembangun menggunakan ciri ini dengan lebih baik. 1. Gunakan fungsi gantian PyCharm menyediakan fungsi gantian berkuasa yang boleh membantu pembangun menggantikan teks dalam kod dengan cepat. Gunakan pintasan Ctrl+R atau klik kanan dalam editor dan pilih Semula
 Penjelasan terperinci tentang cara menggantikan baris baharu dalam PHP
Mar 20, 2024 pm 01:21 PM
Penjelasan terperinci tentang cara menggantikan baris baharu dalam PHP
Mar 20, 2024 pm 01:21 PM
Penjelasan terperinci tentang cara menggantikan baris baharu dalam PHP Dalam pembangunan PHP, kadangkala kita perlu menggantikan atau memproses baris baharu dalam rentetan. Pemisahan baris mungkin dinyatakan secara berbeza pada platform yang berbeza, jadi ia perlu diproses secara seragam untuk memastikan rentetan dipaparkan secara konsisten dalam persekitaran yang berbeza. Artikel ini akan memperkenalkan secara terperinci cara menggantikan baris baharu dalam PHP, termasuk aksara baris baharu biasa dan contoh kod khusus. 1. Aksara baris baharu biasa Dalam sistem pengendalian yang berbeza, perwakilan aksara baris baharu mungkin sedikit berbeza. Watak baris baharu utama termasuk: Windo



