Algoritma kuantum menakluki jenis masalah baharu!

Pada tahun 1994, seorang ahli matematik mengetahui cara membuat komputer kuantum melakukan perkara yang tidak boleh dilakukan oleh komputer klasik biasa. Hasil kerja menunjukkan bahawa, pada dasarnya, mesin berdasarkan peraturan mekanik kuantum boleh menguraikan nombor besar dengan cekap kepada faktor utamanya - tugas yang sangat sukar untuk komputer klasik, yang membentuk sebahagian besar Asas Keselamatan Internet hari ini.

Dengan itu datang gelombang keyakinan. Mungkin, penyelidik percaya, kita akan dapat mencipta algoritma kuantum yang boleh menyelesaikan sejumlah besar masalah yang berbeza.

Tetapi kemajuan telah terhenti. "Ia agak mengecewakan, " kata Ryan O'Donnell dari Universiti Carnegie Mellon "Orang ramai akan berkata, 'Ini bagus, saya pasti kita akan mendapat semua jenis algoritma lain yang menakjubkan,' dan ianya. tidak." Para saintis hanya menemui percepatan yang ketara untuk satu kelas masalah yang sempit dalam set standard yang dipanggil NP, bermakna mereka mempunyai penyelesaian yang boleh disahkan yang cekap - seperti pemfaktoran.

Ini telah berlaku sejak tiga tahun lalu. Kemudian pada bulan April, penyelidik mencipta jenis masalah yang sama sekali baru yang komputer kuantum sepatutnya dapat menyelesaikan lebih cepat daripada komputer klasik. Ia melibatkan pengiraan input proses matematik yang kompleks hanya berdasarkan output yang tidak kemas. Sama ada masalah ini berdiri sendiri atau yang pertama daripada banyak masalah lain masih perlu ditentukan.

"Terdapat rasa teruja," kata Vinod Vaikuntanathan, seorang saintis komputer di MIT "Ramai orang berfikir tentang perkara lain di luar sana. "

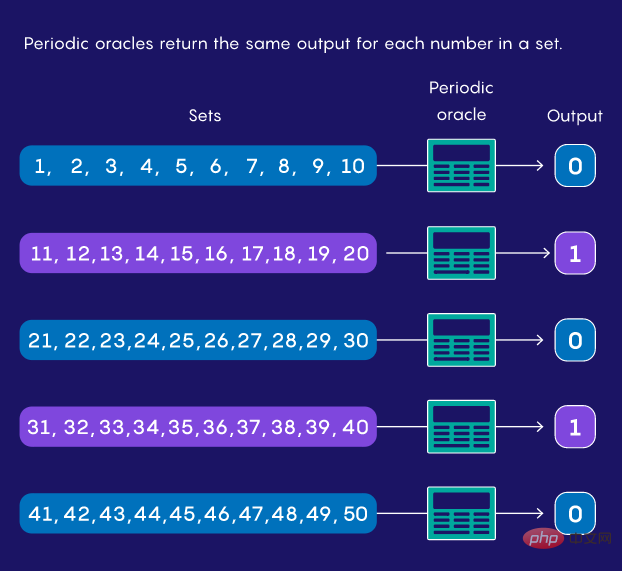
Saintis komputer cuba memahami perkara yang dilakukan oleh komputer kuantum dengan lebih baik dengan mengkaji model matematik yang mewakilinya. Biasanya, mereka membayangkan model komputer kuantum atau klasik dipasangkan dengan komputer ideal yang dipanggil oracle. Oracle adalah seperti fungsi matematik mudah atau program komputer yang mengambil input dan mengeluarkan output yang telah ditetapkan.

Mereka mungkin mempunyai gelagat rawak, mengeluarkan "ya" jika input berada dalam julat rawak (cth., 12 hingga 67) dan "tidak" sebaliknya. Atau ia mungkin berkala, jadi input antara 1 dan 10 mengembalikan "ya", 11 hingga 20 menghasilkan "tidak", 21 hingga 30 sekali lagi menghasilkan "ya", dan seterusnya.

Andaikan anda mempunyai salah satu daripada nubuatan berkala ini, tetapi anda tidak mengetahui tempohnya. Apa yang anda boleh lakukan ialah memberinya nombor dan lihat apa yang ia keluarkan. Seberapa pantas komputer boleh mencari kitaran di bawah kekangan ini? Pada tahun 1993, Daniel Simon, kemudian di Universiti Montreal, mendapati bahawa algoritma kuantum boleh mengira jawapan kepada masalah yang berkait rapat dengan lebih cepat daripada mana-mana algoritma klasik.

Hasil ini membolehkan Simon mengenal pasti salah satu tanda pertama di mana komputer kuantum mungkin mempunyai kelebihan yang ketara. Tetapi apabila dia menyerahkan kertas kerjanya ke persidangan besar, ia ditolak. Kertas itu, bagaimanapun, menarik minat ahli junior jawatankuasa program persidangan, Peter Shor, yang ketika itu bekerja di Bell Laboratories di New Jersey.

Shor terus mendapati bahawa dia boleh mengubah suai algoritma Simon untuk mengira tempoh oracle, jika ia mempunyai satu. Kemudian dia menyedari dia boleh mengubahsuai algoritma sekali lagi untuk menyelesaikan persamaan yang berkelakuan seperti ramalan berkala: persamaan yang menerangkan pemfaktoran yang berkala.

Keputusan Shor adalah bersejarah. Algoritma kuantum yang ditemuinya dengan cepat boleh mengurangkan jumlah yang besar kepada faktor utama konstituennya, sesuatu yang tidak boleh dilakukan oleh algoritma klasik. Pada tahun-tahun berikutnya, penyelidik menemui algoritma kuantum lain yang cekap. Sesetengah daripada mereka, seperti algoritma Shor, malah memberikan kelebihan eksponen, tetapi tiada siapa yang dapat membuktikan kelebihan kuantum yang ketara pada sebarang masalah NP bukan berkala.

Dua saintis komputer, Scott Aaronson dari Universiti Texas di Austin dan Andris Ambainis dari Universiti Latvia, membuat pemerhatian. Bukti kelebihan kuantum nampaknya sentiasa bergantung pada ramalan dengan beberapa struktur bukan rawak, seperti berkala. Pada tahun 2009, mereka membuat spekulasi bahawa tidak akan ada peningkatan yang ketara untuk masalah NP rawak atau tidak berstruktur;

Dugaan mereka mengehadkan keupayaan komputer kuantum. Tetapi ia hanya mengatakan bahawa untuk jenis masalah NP tidak berstruktur tertentu—yang mempunyai jawapan ya atau tidak—tidak ada percepatan yang ketara. Konjektur ini tidak terpakai jika masalah melibatkan mencari jawapan kuantitatif yang lebih spesifik, yang dipanggil masalah carian.

Dengan ini, penyelidik Takashi Yamakawa dari Makmal Informatik Sosial NTT dan Mark Zhandry dari NTT Research dan Princeton University memutuskan untuk menyiasat kajian oleh Oded Regev dalam Eksperimen dengan soalan carian khusus yang dikemukakan pada tahun 2005.

Bayangkan satu set baling cuaca yang semuanya menghala ke arah yang sama. Beri setiap daripada mereka tolakan yang diukur dan biarkan tiupan mempengaruhi arah mereka. Regev mahu menentukan ke mana mereka asalnya ditunjuk berdasarkan hala tuju terakhir mereka. Masalah seperti ini dikenali sebagai "pembelajaran ralat" kerana tujahan dan angin bertindak seperti sumber ralat rawak ke arah asal. Terdapat bukti bahawa kedua-dua algoritma klasik dan kuantum sukar untuk diselesaikan.

Yamakawa dan Zhandry mengubah suai tetapan. Mereka mengubah suai kuasa ini mula menjadikannya lebih mudah diramal. Mereka juga membuat angin ditentukan oleh oracle rawak, jadi dalam beberapa kes ia lebih rawak, tetapi dalam kes lain tidak aktif sepenuhnya.

Dengan pengubahsuaian ini, para penyelidik mendapati bahawa algoritma kuantum boleh mencari arah awal dengan berkesan. Mereka juga membuktikan bahawa mana-mana algoritma klasik mesti diperlahankan oleh faktor eksponen. Seperti Shor, mereka kemudian menyesuaikan algoritma untuk menyelesaikan versi masalah yang realistik, menggantikan ramalan dengan persamaan matematik sebenar.

Para saintis komputer masih berusaha untuk memahami dan menyelesaikan masalah ini. Vaikuntanathan membandingkan ini dengan situasi berbeza yang berlaku semasa melakukan pemampatan data: apabila maklumat dimampatkan, dua bit secara tidak sengaja boleh memerah ke tempat yang sama, sekali gus menimpanya. Masalah menjangkakan perlanggaran ini terlebih dahulu untuk mengelakkannya mempunyai beberapa persamaan. "Ini adalah kelas masalah yang pada asasnya kelihatan seperti ini, " katanya "Mungkin masalah ini boleh diselesaikan secara kuantum, Walaupun pada versi komputer kuantum yang masih baru, masalah tidak berstruktur seperti masalah baru dapat diselesaikan, memberikan satu masalah." cara untuk menguji mereka. Ideanya ialah masalah tidak berstruktur mungkin memerlukan lebih sedikit sumber untuk memprogram atau kurang sensitif kepada bunyi kerana ia sudah rawak. Tetapi setakat ini, masalah baru ini masih kelihatan terlalu maju untuk diselesaikan oleh komputer kuantum sedia ada. "Itu soalan yang pelik. Saya tidak terfikir untuk mentakrifkannya," kata Aaronson, "tetapi jika difikirkan semula, ia mempunyai beberapa ciri yang sangat bagus."

Keputusan ini memberikan contoh pertama kelebihan kuantum yang ketara pada masalah NP tidak berstruktur. Adakah banyak masalah lain dalam dunia kuantum akan berubah daripada hampir tidak dapat diselesaikan kepada boleh diselesaikan? Kini terdapat lebih banyak sebab untuk berfikir demikian. "Ini sedikit sebanyak mengubah pandangan kami tentang masalah yang boleh diselesaikan oleh komputer kuantum," kata O'Donnell.

Atas ialah kandungan terperinci Algoritma kuantum menakluki jenis masalah baharu!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!