
Struktur data pelaksanaan jenis int di dalam cpython adalah seperti berikut:
typedef struct _longobject PyLongObject;
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
#define PyObject_VAR_HEAD PyVarObject ob_base;
typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
_PyObject_HEAD_EXTRA
Py_ssize_t ob_refcnt;
struct _typeobject *ob_type;
} PyObject;Struktur data di atas diwakili secara grafik seperti yang ditunjukkan dalam rajah di bawah:
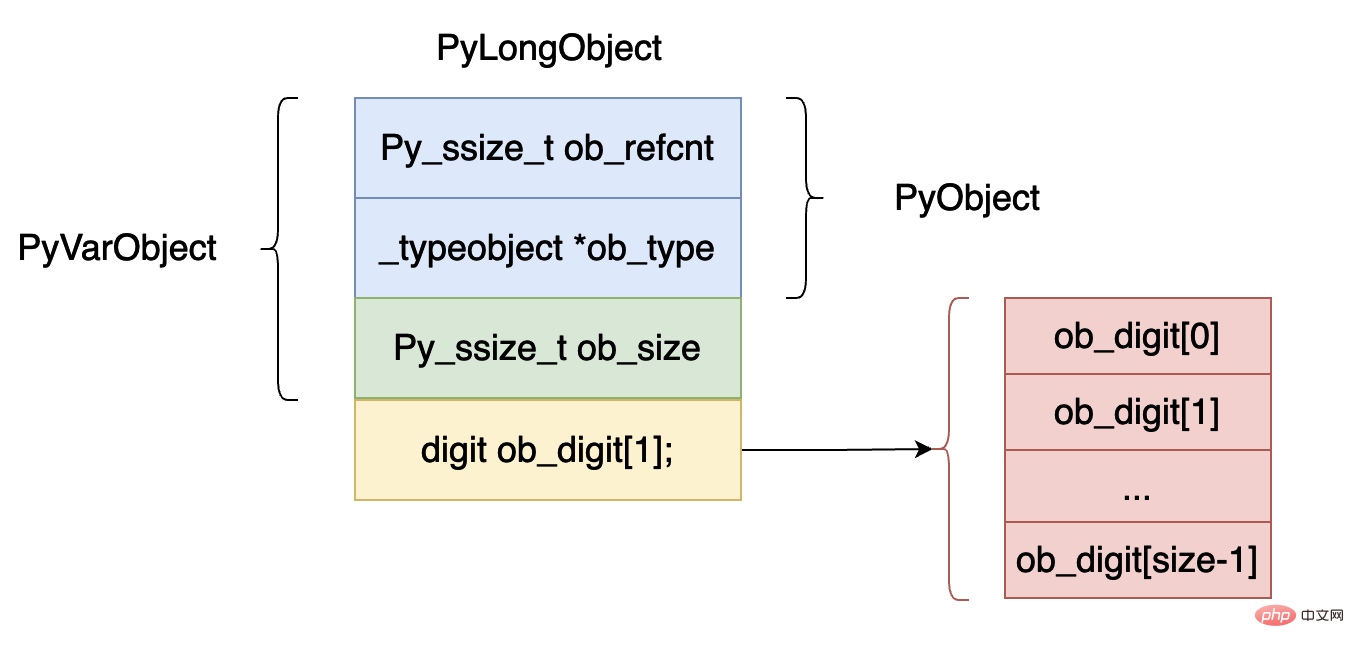
ob_refcnt, mewakili bilangan rujukan objek Ini sangat berguna untuk pengumpulan sampah Nanti kita akan menganalisis bahagian kutipan sampah di maya mesin.
ob_type, menunjukkan jenis data objek ini Dalam python, kadangkala perlu menilai jenis data data, seperti isinstance, type, kedua-dua kata kunci ini akan. digunakan medan.
ob_size, medan ini menunjukkan bilangan elemen yang terdapat dalam ob_digit tatasusunan objek integer ini.
Jenis digit sebenarnya ialah takrifan makro bagi jenis uint32_t, yang mewakili data integer 32-bit.
Pertama sekali, kita tahu bahawa integer dalam python tidak akan melimpah, itulah sebabnya PyLongObject menggunakan tatasusunan. Dalam pelaksanaan dalaman cpython, integer termasuk 0, nombor positif dan nombor negatif Berkenaan dengan ini, terdapat peraturan berikut dalam cpython:
ob_size, yang menyimpan panjang tatasusunan. , ob_size Apabila ia lebih besar daripada 0, nombor positif disimpan apabila ob_size kurang daripada 0, nombor negatif disimpan.
ob_digit, menyimpan nilai mutlak integer. Seperti yang kami nyatakan sebelum ini, ob_digit ialah data 32-bit, tetapi hanya 30 bit pertama digunakan secara dalaman dalam cpython, hanya untuk mengelakkan masalah limpahan.
Mari kita gunakan beberapa contoh untuk memahami peraturan di atas secara mendalam:
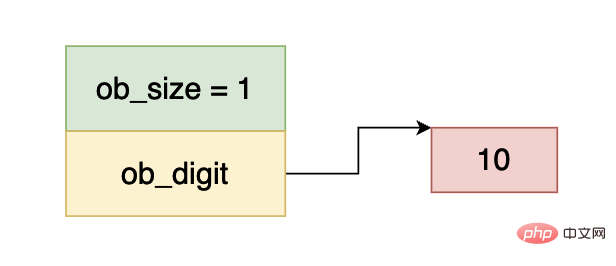
Dalam rajah di atas, ob_size lebih besar daripada 0 , menunjukkan bahawa Nombor ini ialah nombor positif, dan ob_digit menunjuk kepada data int32 Nilai nombor adalah sama dengan 10, jadi nombor di atas mewakili integer 10.
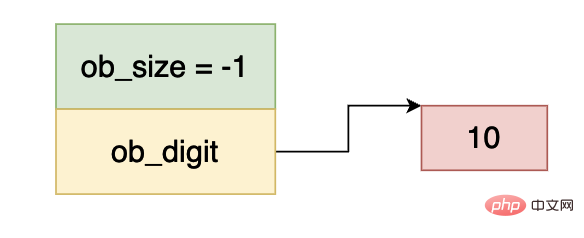
Begitu juga, ob_size adalah kurang daripada 0, dan ob_digit bersamaan dengan 10, jadi data dalam gambar di atas mewakili -10.

Di atas ialah contoh tatasusunan ob_digit dengan panjang 2. Data yang diwakili di atas adalah seperti berikut:
1⋅2 0 +1⋅21+1⋅22+...+1⋅229+0⋅230+0&sdot ;231+1⋅232
Oleh kerana kami hanya menggunakan 30 bit pertama untuk setiap elemen tatasusunan, jadi kepada data integer kedua masa sepadan dengan 230. Anda boleh memahami keseluruhan proses pengiraan berdasarkan keputusan di atas.

Perkara di atas sangat mudah:
&tolak;(1⋅20+1⋅21+1⋅22+...+1⋅229+0⋅230+0⋅231 + 1⋅232)
Untuk mengelakkan kerap mencipta beberapa integer yang biasa digunakan dan mempercepatkan pelaksanaan program, kita boleh menggunakan beberapa integer yang biasa digunakan untuk Cache dahulu dan kembalikan data secara terus jika perlu. Kod yang berkaitan dalam cpython adalah seperti berikut: (Selang data cache dalam kumpulan integer kecil ialah [-5, 256])
#define NSMALLPOSINTS 257 #define NSMALLNEGINTS 5 static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];
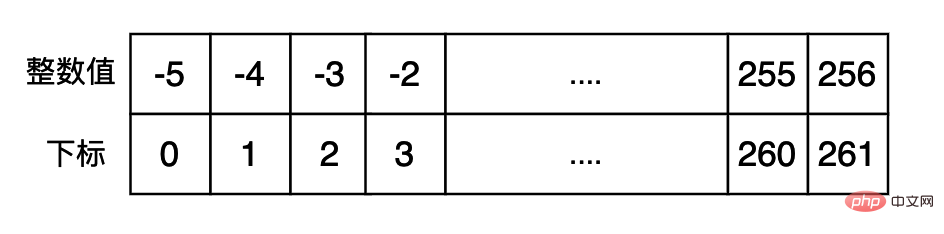
Kami menggunakan yang berikut kod Uji untuk melihat sama ada data dalam kumpulan integer kecil digunakan Jika ya, nilai pulangan id() mereka adalah sama untuk data dalam kumpulan integer kecil Fungsi terbina dalam id mengembalikan memori Python alamat.
>>> a = 1 >>> b = 2 >>> c = 1 >>> id(a), id(c) (4343136496, 4343136496) >>> a = -6 >>> c = -6 >>> id(a), id(c) (4346020624, 4346021072) >>> a = 257 >>> b = 257 >>> id(a), id(c) (4346021104, 4346021072) >>>
Apa yang dapat kita lihat daripada keputusan di atas ialah untuk nilai dalam selang [-5, 256], nilai pulangan id sememangnya sama, dan nilai pulangan tidak berada dalam selang ini Tidak sama.
Kami juga boleh melaksanakan helah kecil dengan ciri ini, iaitu mencari ruang memori yang diduduki oleh objek PyLongObject, kerana kami boleh menggunakan alamat memori pertama bagi dua data -5 dan 256, dan kemudian menambah alamat ini Dengan menolak, anda boleh mendapatkan saiz ruang memori yang diduduki oleh 261 PyLongObjects (perhatikan bahawa walaupun terdapat 262 data dalam kumpulan integer kecil, data terakhir ialah alamat pertama memori, bukan alamat terakhir, jadi ada hanya 261 data), jadi kami Anda boleh mencari saiz memori objek PyLongObject.
>>> a = -5 >>> b = 256 >>> (id(b) - id(a)) / 261 32.0 >>>
Daripada output di atas kita dapat melihat bahawa objek PyLongObject menduduki 32 bait. Kita boleh menggunakan program C berikut untuk melihat ruang memori sebenar yang diduduki oleh PyLongObject.
#include "Python.h"
#include <stdio.h>
int main()
{
printf("%ld\n", sizeof(PyLongObject));
return 0;
}Output program di atas adalah seperti berikut:

Dua keputusan di atas adalah sama, sekali gus mengesahkan idea kami.
Kod teras untuk mendapatkan data daripada kumpulan integer kecil adalah seperti berikut:
static PyObject *
get_small_int(sdigit ival)
{
PyObject *v;
assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
Py_INCREF(v);
return v;
}如果你了解过大整数加法就能够知道,大整数加法的具体实现过程了,在 cpython 内部的实现方式其实也是一样的,就是不断的进行加法操作然后进行进位操作。
#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的绝对值
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
// 首先获得两个整型数据的 size
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
// 确保 a 保存的数据 size 是更大的
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 创建一个新的 PyLongObject 对象,而且数组的长度是 size_a + 1
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
// 下面就是整个加法操作的核心
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
// 将低 30 位的数据保存下来
z->ob_digit[i] = carry & PyLong_MASK;
// 将 carry 右移 30 位,如果上面的加法有进位的话 刚好可以在下一次加法当中使用(注意上面的 carry)
// 使用的是 += 而不是 =
carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
}
// 将剩下的长度保存 (因为 a 的 size 是比 b 大的)
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
// 最后保存高位的进位
z->ob_digit[i] = carry;
return long_normalize(z); // long_normalize 这个函数的主要功能是保证 ob_size 保存的是真正的数据的长度 因为可以是一个正数加上一个负数 size 还变小了
}
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
PyLongObject *result;
/* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
sizeof(digit)*size. Previous incarnations of this code used
sizeof(PyVarObject) instead of the offsetof, but this risks being
incorrect in the presence of padding between the PyVarObject header
and the digits. */
if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
PyErr_SetString(PyExc_OverflowError,
"too many digits in integer");
return NULL;
}
// offsetof 会调用 gcc 的一个内嵌函数 __builtin_offsetof
// offsetof(PyLongObject, ob_digit) 这个功能是得到 PyLongObject 对象 字段 ob_digit 之前的所有字段所占的内存空间的大小
result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
size*sizeof(digit));
if (!result) {
PyErr_NoMemory();
return NULL;
}
// 将对象的 result 的引用计数设置成 1
return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
static PyLongObject *
long_normalize(PyLongObject *v)
{
Py_ssize_t j = Py_ABS(Py_SIZE(v));
Py_ssize_t i = j;
while (i > 0 && v->ob_digit[i-1] == 0)
--i;
if (i != j)
Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
return v;
}Atas ialah kandungan terperinci Apakah prinsip pelaksanaan integer dalam mesin maya Python?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




