 Peranti teknologi
Peranti teknologi
 AI
AI
 Pembelajaran pengukuhan menemui algoritma pendaraban matriks, DeepMind sekali lagi muncul pada kulit Alam dan melancarkan AlphaTensor
Pembelajaran pengukuhan menemui algoritma pendaraban matriks, DeepMind sekali lagi muncul pada kulit Alam dan melancarkan AlphaTensor
Pembelajaran pengukuhan menemui algoritma pendaraban matriks, DeepMind sekali lagi muncul pada kulit Alam dan melancarkan AlphaTensor
Algoritma telah membantu ahli matematik melakukan operasi asas selama beribu-ribu tahun. Lama dahulu, orang Mesir purba mencipta algoritma untuk mendarab dua nombor tanpa memerlukan jadual pendaraban. Ahli matematik Yunani Euclid menerangkan algoritma untuk mengira pembahagi sepunya terbesar yang masih digunakan hari ini. Semasa Zaman Keemasan Islam, ahli matematik Parsi Muhammad ibn Musa al-Khwarizmi telah mencipta algoritma baharu untuk menyelesaikan persamaan linear dan kuadratik yang akan memberi impak yang mendalam kepada penyelidikan seterusnya.
Malah ada pepatah tentang kemunculan perkataan algoritma: perkataan al-Khawarizmi atas nama ahli matematik Parsi Muhammad ibn Musa al-Khwarizmi diterjemahkan ke dalam bahasa Latin sebagai Makna Algoritmi, yang membawa kepada perkataan algoritma. Walau bagaimanapun, walaupun hari ini kita sangat biasa dengan algoritma, kita boleh mempelajarinya dari bilik darjah, dan sering menghadapinya dalam bidang penyelidikan saintifik Nampaknya seluruh masyarakat menggunakan algoritma, tetapi proses menemui algoritma baru sangat sukar .
Kini, DeepMind menggunakan AI untuk menemui algoritma baharu.
Dalam kertas kulit terbitan terbaru Nature, "Menemui algoritma pendaraban matriks yang lebih pantas dengan pembelajaran pengukuhan", DeepMind mencadangkan AlphaTensor dan menyatakan bahawa ia adalah yang pertama digunakan untuk fungsi asas seperti pendaraban matriks sistem kecerdasan buatan yang ditugaskan untuk menemui algoritma yang baru, cekap dan betul. Ringkasnya, menggunakan AlphaTensor membolehkan anda menemui algoritma baharu. Penyelidikan memberi penerangan tentang masalah matematik yang tidak dapat diselesaikan selama 50 tahun: mencari cara terpantas untuk mendarab dua matriks.


- Alamat kertas : https://www.nature.com/articles/s41586-022-05172-4
- Alamat GitHub: https://github.com/deepmind /alphatensor
AlphaTensor dibina berdasarkan AlphaZero, iaitu catur, Agen yang boleh mengalahkan manusia dalam permainan papan seperti Go dan Shogi. Kerja ini menunjukkan peralihan AlphaZero daripada digunakan untuk permainan kepada digunakan buat kali pertama untuk menyelesaikan masalah matematik yang tidak dapat diselesaikan.
Pendaraban Matriks
Pendaraban matriks ialah salah satu operasi paling mudah dalam algebra dan biasanya diajar dalam kelas matematik sekolah menengah. Tetapi di luar bilik darjah, operasi matematik yang sederhana ini mempunyai impak yang besar dalam dunia digital kontemporari dan terdapat di mana-mana dalam pengkomputeran moden.
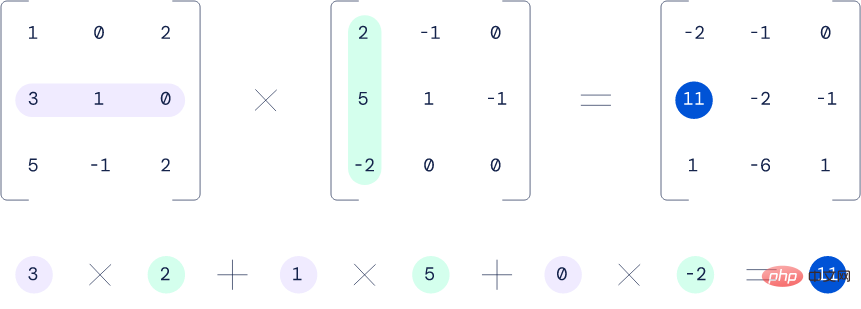
Contoh pendaraban dua matriks 3x3.
Anda mungkin tidak perasan bahawa pendaraban matriks tersembunyi di mana-mana dalam kehidupan kita, seperti pemprosesan imej dalam telefon pintar, mengecam arahan suara, Ia berfungsi pengiraan di belakang tabir seperti menjana grafik untuk permainan komputer. Syarikat di seluruh dunia sanggup menghabiskan banyak masa dan wang membangunkan perkakasan pengkomputeran untuk menyelesaikan pendaraban matriks dengan cekap. Oleh itu, walaupun peningkatan kecil dalam kecekapan pendaraban matriks boleh mempunyai kesan yang meluas.
Selama berabad-abad, ahli matematik telah menganggap algoritma pendaraban matriks piawai sebagai algoritma yang paling cekap. Tetapi pada tahun 1969, ahli matematik Jerman Volken Strassen mengejutkan dunia matematik dengan membuktikan bahawa algoritma yang lebih baik memang wujud.

Membandingkan algoritma standard dengan algoritma Strassen, yang terakhir melakukan satu operasi pendaraban yang kurang, iaitu 7 kali. Yang pertama memerlukan 8 kali, dan kecekapan keseluruhan bertambah baik.
Dengan mengkaji matriks yang sangat kecil (saiz 2x2), Strassen menemui cara bijak untuk menggabungkan istilah matriks untuk menghasilkan algoritma Pantas yang lebih besar . Dalam dekad berikutnya, penyelidik telah mengkaji matriks yang lebih besar, malah mencari kaedah yang cekap untuk mendarab matriks 3x3 masih belum dapat diselesaikan.
Penyelidikan terkini daripada DeepMind meneroka bagaimana teknologi AI moden memacu penemuan automatik algoritma pendaraban matriks baharu. Berdasarkan kemajuan dalam intuisi manusia, algoritma yang ditemui oleh AlphaTensor adalah lebih cekap daripada banyak kaedah SOTA untuk matriks yang lebih besar. Kajian itu menunjukkan bahawa algoritma rekaan AI mengatasi prestasi yang direka oleh manusia, satu langkah penting ke hadapan dalam bidang penemuan algoritma.
Proses dan kemajuan automasi penemuan algoritma
Mula-mula menukar masalah menemui algoritma yang cekap untuk pendaraban matriks kepada permainan pemain tunggal. Antaranya, papan ialah tensor tiga dimensi (susun nombor) yang digunakan untuk menangkap seberapa betul algoritma semasa. Melalui satu set pergerakan yang dibenarkan sepadan dengan arahan algoritma, pemain cuba mengubah suai tensor dan mengembalikan entrinya kepada sifar.
Apabila pemain berjaya melakukan ini, algoritma pendaraban matriks yang terbukti betul dijana untuk mana-mana pasangan matriks, dan kecekapannya diukur dengan bilangan langkah yang diambil untuk mensifarkan tensor .
Permainan ini sangat mencabar dan bilangan algoritma yang mungkin untuk dipertimbangkan adalah jauh lebih besar daripada bilangan atom di alam semesta, walaupun untuk kes sekecil pendaraban matriks. Berbanding dengan permainan Go, yang telah menjadi cabaran AI selama beberapa dekad, permainan ini mempunyai 30 susunan magnitud lebih banyak kemungkinan pergerakan setiap gerakan (satu tetapan yang dipertimbangkan DeepMind ialah 10^33+.)
Untuk menangani cabaran domain yang jauh berbeza daripada permainan tradisional, DeepMind telah membangunkan beberapa komponen utama, termasuk seni bina rangkaian saraf baharu yang menggabungkan bias induktif khusus masalah, program untuk menjana data sintetik yang berguna dan cara A. untuk mengambil kesempatan daripada simetri masalah.
Seterusnya, DeepMind melatih ejen yang dipanggil AlphaTensor menggunakan pembelajaran tetulang untuk bermain permainan, bermula tanpa pengetahuan tentang algoritma pendaraban matriks sedia ada. Dengan pembelajaran, AlphaTensor bertambah baik secara beransur-ansur dari semasa ke semasa, menemui semula algoritma matriks pantas sejarah (seperti algoritma Strassen) dan menemui algoritma yang lebih pantas daripada yang diketahui sebelum ini.
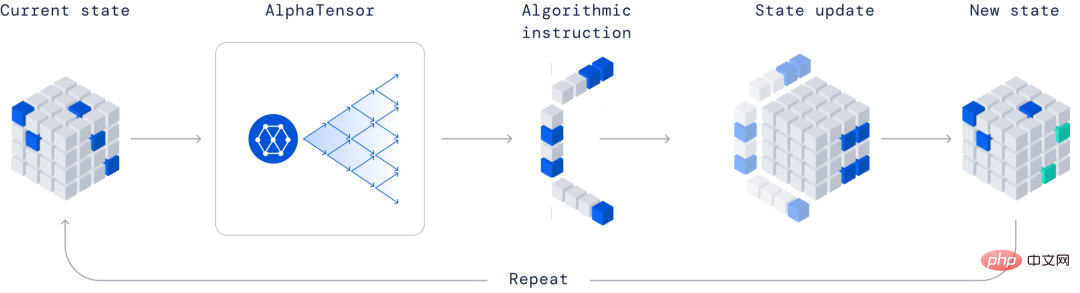
AlphaTensor ialah permainan pemain tunggal di mana matlamatnya adalah untuk mencari algoritma pendaraban matriks yang betul. Keadaan permainan ialah tatasusunan padu nombor (kelabu mewakili 0, biru mewakili 1, dan hijau mewakili - 1) yang mewakili baki kerja yang perlu dilakukan.
Sebagai contoh, jika algoritma tradisional yang diajar di sekolah boleh menggunakan 100 pendaraban untuk melengkapkan pendaraban matriks 4x5 dan 5x5, melalui kecerdasan manusia Hikmah. boleh menurunkan nombor itu kepada 80 kali ganda. Sebagai perbandingan, algoritma yang ditemui oleh AlphaTensor mencapai operasi yang sama menggunakan hanya 76 pendaraban, seperti yang ditunjukkan dalam imej di bawah.

Selain contoh di atas, algoritma yang ditemui oleh AlphaTensor juga menambah baik susunan kedua Strassen dalam medan terhingga untuk algoritma kali pertama. Algoritma ini untuk mendarab matriks kecil boleh digunakan sebagai primitif untuk mendarab matriks yang lebih besar dari sebarang saiz.
AlphaTensor juga menemui pelbagai set algoritma dengan kerumitan SOTA, dengan sehingga beribu-ribu algoritma pendaraban matriks bagi setiap saiz, menunjukkan bahawa ruang untuk algoritma pendaraban matriks adalah lebih besar daripada yang difikirkan sebelum ini. Kaya.
Algoritma dalam ruang kaya ini mempunyai sifat matematik dan praktikal yang berbeza. Mengambil kesempatan daripada kepelbagaian ini, DeepMind menala AlphaTensor untuk menemui secara khusus algoritma yang berjalan pantas pada perkakasan tertentu (cth., GPU Nvidia V100, Google TPU v2). Algoritma ini melakukan pendaraban matriks yang besar 10-20% lebih pantas daripada algoritma yang biasa digunakan pada perkakasan yang sama, menunjukkan fleksibiliti AlphaTensor dalam mengoptimumkan objektif sewenang-wenangnya.
AlphaTensor mempunyai sasaran yang sepadan dengan masa jalan algoritma. Apabila algoritma pendaraban matriks yang betul ditemui, ia ditanda aras pada perkakasan yang ditentukan dan kemudian diumpan semula kepada AlphaTensor untuk mempelajari algoritma yang lebih cekap pada perkakasan yang ditentukan.
Implikasi untuk penyelidikan dan aplikasi masa hadapan
Dari perspektif matematik, keputusan DeepMind boleh membimbing teori kerumitan, yang bertujuan untuk mengenal pasti algoritma terpantas untuk menyelesaikan masalah pengiraan. AlphaTensor membantu memperdalam pemahaman kami tentang kekayaan algoritma pendaraban matriks dengan meneroka ruang algoritma yang mungkin dengan lebih cekap daripada kaedah sebelumnya.
Selain itu, oleh kerana pendaraban matriks ialah komponen teras bagi banyak tugas pengkomputeran, termasuk grafik komputer, komunikasi digital, latihan rangkaian saraf dan pengkomputeran saintifik, algoritma yang ditemui oleh AlphaTensor boleh meningkatkan fungsi ini dengan ketara. bidang kecekapan pengiraan.
Walaupun artikel ini hanya memfokuskan pada masalah khusus pendaraban matriks, DeepMind berharap dapat memberi inspirasi kepada lebih ramai orang untuk menggunakan AI untuk membimbing penemuan algoritma untuk tugas pengkomputeran asas yang lain. Selain itu, penyelidikan DeepMind juga menunjukkan bahawa algoritma AlphaZero yang berkuasa jauh melangkaui bidang permainan tradisional dan boleh membantu menyelesaikan masalah terbuka dalam bidang matematik.
Pada masa hadapan, DeepMind berharap dapat menggunakan lebih banyak kecerdasan buatan untuk membantu masyarakat menyelesaikan beberapa cabaran paling penting dalam matematik dan sains berdasarkan penyelidikan mereka.
Atas ialah kandungan terperinci Pembelajaran pengukuhan menemui algoritma pendaraban matriks, DeepMind sekali lagi muncul pada kulit Alam dan melancarkan AlphaTensor. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Petua Konfigurasi Firewall Pelayan Mel Debian
Apr 13, 2025 am 11:42 AM
Petua Konfigurasi Firewall Pelayan Mel Debian
Apr 13, 2025 am 11:42 AM
Mengkonfigurasi firewall pelayan Mail Debian adalah langkah penting dalam memastikan keselamatan pelayan. Berikut adalah beberapa kaedah konfigurasi firewall yang biasa digunakan, termasuk penggunaan iptables dan firewalld. Gunakan iptables untuk mengkonfigurasi firewall untuk memasang iptables (jika belum dipasang): sudoapt-getupdateudoapt-getinstalliplesview peraturan iptables semasa: konfigurasi sudoiptable-l
 Cara Menetapkan Tahap Log Debian Apache
Apr 13, 2025 am 08:33 AM
Cara Menetapkan Tahap Log Debian Apache
Apr 13, 2025 am 08:33 AM
Artikel ini menerangkan cara menyesuaikan tahap pembalakan pelayan Apacheweb dalam sistem Debian. Dengan mengubah suai fail konfigurasi, anda boleh mengawal tahap maklumat log yang direkodkan oleh Apache. Kaedah 1: Ubah suai fail konfigurasi utama untuk mencari fail konfigurasi: Fail konfigurasi apache2.x biasanya terletak di direktori/etc/apache2/direktori. Nama fail mungkin apache2.conf atau httpd.conf, bergantung pada kaedah pemasangan anda. Edit Fail Konfigurasi: Buka Fail Konfigurasi dengan Kebenaran Root Menggunakan Editor Teks (seperti Nano): Sudonano/ETC/APACHE2/APACHE2.CONF
 Cara Mengoptimumkan Prestasi Debian Readdir
Apr 13, 2025 am 08:48 AM
Cara Mengoptimumkan Prestasi Debian Readdir
Apr 13, 2025 am 08:48 AM
Dalam sistem Debian, panggilan sistem Readdir digunakan untuk membaca kandungan direktori. Jika prestasinya tidak baik, cuba strategi pengoptimuman berikut: Memudahkan bilangan fail direktori: Split direktori besar ke dalam pelbagai direktori kecil sebanyak mungkin, mengurangkan bilangan item yang diproses setiap panggilan readdir. Dayakan Caching Kandungan Direktori: Bina mekanisme cache, kemas kini cache secara teratur atau apabila kandungan direktori berubah, dan mengurangkan panggilan kerap ke Readdir. Cafh memori (seperti memcached atau redis) atau cache tempatan (seperti fail atau pangkalan data) boleh dipertimbangkan. Mengamalkan struktur data yang cekap: Sekiranya anda melaksanakan traversal direktori sendiri, pilih struktur data yang lebih cekap (seperti jadual hash dan bukannya carian linear) untuk menyimpan dan mengakses maklumat direktori
 Cara Melaksanakan Penyortiran Fail oleh Debian Readdir
Apr 13, 2025 am 09:06 AM
Cara Melaksanakan Penyortiran Fail oleh Debian Readdir
Apr 13, 2025 am 09:06 AM
Dalam sistem Debian, fungsi Readdir digunakan untuk membaca kandungan direktori, tetapi urutan yang dikembalikannya tidak ditentukan sebelumnya. Untuk menyusun fail dalam direktori, anda perlu membaca semua fail terlebih dahulu, dan kemudian menyusunnya menggunakan fungsi QSORT. Kod berikut menunjukkan cara menyusun fail direktori menggunakan ReadDir dan QSORT dalam sistem Debian:#termasuk#termasuk#termasuk#termasuk // fungsi perbandingan adat, yang digunakan untuk qSortintCompare (Constvoid*A, Constvoid*b) {Returnstrcmp (*(*(*(*(*(*(*(*(*(*(*(*(*(*(*(*(*(
 Bagaimana Debian Readdir Bersepadu Dengan Alat Lain
Apr 13, 2025 am 09:42 AM
Bagaimana Debian Readdir Bersepadu Dengan Alat Lain
Apr 13, 2025 am 09:42 AM
Fungsi Readdir dalam sistem Debian adalah panggilan sistem yang digunakan untuk membaca kandungan direktori dan sering digunakan dalam pengaturcaraan C. Artikel ini akan menerangkan cara mengintegrasikan Readdir dengan alat lain untuk meningkatkan fungsinya. Kaedah 1: Menggabungkan Program Bahasa C dan Pipeline Pertama, tulis program C untuk memanggil fungsi Readdir dan output hasilnya:#termasuk#termasuk#includeintMain (intargc, char*argv []) {dir*dir; structdirent*entry; if (argc! = 2) {
 Kaedah pemasangan sijil SSL Server Server Debian
Apr 13, 2025 am 11:39 AM
Kaedah pemasangan sijil SSL Server Server Debian
Apr 13, 2025 am 11:39 AM
Langkah -langkah untuk memasang sijil SSL pada pelayan mel Debian adalah seperti berikut: 1. Pasang OpenSSL Toolkit terlebih dahulu, pastikan bahawa OpenSSL Toolkit telah dipasang pada sistem anda. Jika tidak dipasang, anda boleh menggunakan arahan berikut untuk memasang: sudoapt-getupdateudoapt-getinstallopenssl2. Menjana permintaan kunci dan sijil peribadi seterusnya, gunakan OpenSSL untuk menjana kunci peribadi RSA 2048-bit dan permintaan sijil (CSR): Membuka
 Bagaimana Debian OpenSSL Menghalang Serangan Man-dalam-Middle
Apr 13, 2025 am 10:30 AM
Bagaimana Debian OpenSSL Menghalang Serangan Man-dalam-Middle
Apr 13, 2025 am 10:30 AM
Dalam sistem Debian, OpenSSL adalah perpustakaan penting untuk pengurusan penyulitan, penyahsulitan dan sijil. Untuk mengelakkan serangan lelaki-dalam-pertengahan (MITM), langkah-langkah berikut boleh diambil: Gunakan HTTPS: Pastikan semua permintaan rangkaian menggunakan protokol HTTPS dan bukannya HTTP. HTTPS menggunakan TLS (Protokol Keselamatan Lapisan Pengangkutan) untuk menyulitkan data komunikasi untuk memastikan data tidak dicuri atau diganggu semasa penghantaran. Sahkan Sijil Pelayan: Sahkan secara manual Sijil Pelayan pada klien untuk memastikan ia boleh dipercayai. Pelayan boleh disahkan secara manual melalui kaedah perwakilan urlSession
 Cara Melakukan Pengurusan Log Debian Hadoop
Apr 13, 2025 am 10:45 AM
Cara Melakukan Pengurusan Log Debian Hadoop
Apr 13, 2025 am 10:45 AM
Menguruskan Log Hadoop pada Debian, anda boleh mengikuti langkah-langkah berikut dan amalan terbaik: Agregasi log membolehkan pengagregatan log: tetapkan benang.log-agregasi-enable untuk benar dalam fail benang-site.xml untuk membolehkan pengagregatan log. Konfigurasikan dasar pengekalan log: tetapkan yarn.log-aggregasi.Retain-seconds Untuk menentukan masa pengekalan log, seperti 172800 saat (2 hari). Nyatakan Laluan Penyimpanan Log: Melalui Benang



