
遗传算法 ialah kaedah pencarian dan pengoptimuman global stokastik yang dibangunkan untuk meniru mekanisme evolusi biologi dalam alam semula jadi. Ia menggunakan teori evolusi Darwin dan teori genetik Mendel. Intipatinya ialah kaedah carian global yang cekap, selari, yang boleh memperoleh dan mengumpul pengetahuan secara automatik tentang ruang carian semasa proses carian, dan mengawal proses carian secara adaptif untuk mendapatkan penyelesaian yang optimum. Operasi algoritma genetik menggunakan prinsip survival of the fittest untuk berturut-turut menjana penyelesaian hampir optimum dalam populasi penyelesaian berpotensi Dalam setiap generasi algoritma genetik, mengikut nilai kecergasan individu dalam domain masalah dan daripada genetik semula jadi kaedah pembinaan semula yang dipinjam daripada kesusasteraan Cina digunakan untuk pemilihan individu bagi menghasilkan penyelesaian anggaran baharu. Proses ini membawa kepada evolusi individu dalam populasi, dan individu baharu yang terhasil lebih baik disesuaikan dengan persekitaran berbanding individu asal, sama seperti perubahan dalam alam semula jadi.
(1) Permulaan: Tetapkan pembilang generasi evolusi t=0, tetapkan generasi evolusi maksimum T, kebarangkalian silang silang, kebarangkalian mutasi dan jana secara rawak M individu sebagai populasi awal P
(2) Penilaian individu: Kira kecergasan setiap individu dalam populasi P
(3) Operasi pemilihan: Gunakan operator pemilihan kepada populasi. Berdasarkan kecergasan individu, pilih individu yang optimum untuk diwarisi terus kepada generasi seterusnya atau menjana individu baharu melalui silang berpasangan dan kemudian mewarisi kepada generasi seterusnya
(4) Operasi silang silang: Di bawah kawalan kebarangkalian silang silang, populasi Individu dalam populasi disilang secara berpasangan
(5) Operasi mutasi: Di bawah kawalan kebarangkalian mutasi, individu dalam populasi bermutasi, iaitu gen individu tertentu diselaraskan secara rawak
(6) Selepas operasi pemilihan, silang dan mutasi, populasi generasi seterusnya P1 diperolehi.
Ulang perkara di atas (1)-(6) sehingga penjanaan genetik ialah T, dan gunakan individu dengan kecergasan optimum yang diperoleh semasa proses evolusi sebagai output penyelesaian optimum, dan tamatkan pengiraan.
Masalah Jurujual Perjalanan (TSP): Terdapat n bandar Seorang jurujual perlu bermula dari salah satu bandar, melawat semua bandar, dan kemudian kembali ke bandar tempat dia bermula.
Sesetengah konvensyen perlu dibuat apabila menggunakan algoritma genetik untuk menyelesaikan masalah TSP Gen ialah satu set jujukan bandar, dan kesesuaian adalah satu pertiga daripada jarak dan jujukan bandar mengikut gen ini. .
import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典,防止下面被当成列表
cities={}
for line in data:
#原始数据以\n换行,将其替换掉
line=line.replace("\n","")
#最后一行以EOF为标志,如果读到就证明读完了,退出循环
if(line=="EOF"):
break
#空格分割城市编号和城市的坐标
city=line.split(" ")
map(int,city)
#将城市数据添加到cities中
cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
# 计算适应度,也就是距离分之一,这里用伪欧氏距离
def calcfit(gene):
sum=0
#最后要回到初始城市所以从-1,也就是最后一个城市绕一圈到最后一个城市
for i in range(-1,len(gene)-1):
nowcity=gene[i]
nextcity=gene[i+1]
nowloc=cities[nowcity]
nextloc=cities[nextcity]
sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
return 1/sum
# 每个个体的类,方便根据基因计算适应度
class Person:
def __init__(self,gene):
self.gene=gene
self.fit=calcfit(gene)
class Group:
def __init__(self):
self.GroupSize=100 #种群规模
self.GeneSize=48 #基因数量,也就是城市数量
self.initGroup()
self.upDate()
#初始化种群,随机生成若干个体
def initGroup(self):
self.group=[]
i=0
while(i<self.GroupSize):
i+=1
#gene如果在for以外生成只会shuffle一次
gene=[i+1 for i in range(self.GeneSize)]
random.shuffle(gene)
tmpPerson=Person(gene)
self.group.append(tmpPerson)
#获取种群中适应度最高的个体
def getBest(self):
bestFit=self.group[0].fit
best=self.group[0]
for person in self.group:
if(person.fit>bestFit):
bestFit=person.fit
best=person
return best
#计算种群中所有个体的平均距离
def getAvg(self):
sum=0
for p in self.group:
sum+=1/p.fit
return sum/len(self.group)
#根据适应度,使用轮盘赌返回一个个体,用于遗传交叉
def getOne(self):
#section的简称,区间
sec=[0]
sumsec=0
for person in self.group:
sumsec+=person.fit
sec.append(sumsec)
p=random.random()*sumsec
for i in range(len(sec)):
if(p>sec[i] and p<sec[i+1]):
#这里注意区间是比个体多一个0的
return self.group[i]
#更新种群相关信息
def upDate(self):
self.best=self.getBest()
# 遗传算法的类,定义了遗传、交叉、变异等操作
class GA:
def __init__(self):
self.group=Group()
self.pCross=0.35 #交叉率
self.pChange=0.1 #变异率
self.Gen=1 #代数
#变异操作
def change(self,gene):
#把列表随机的一段取出然后再随机插入某个位置
#length是取出基因的长度,postake是取出的位置,posins是插入的位置
geneLenght=len(gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(0, geneLenght - 1)
newGene = gene[:] # 产生一个新的基因序列,以免变异的时候影响父种群
newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
return newGene
#交叉操作
def cross(self,p1,p2):
geneLenght=len(p1.gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(index1, geneLenght - 1)
tempGene = p2.gene[index1:index2] # 交叉的基因片段
newGene = []
p1len = 0
for g in p1.gene:
if p1len == index1:
newGene.extend(tempGene) # 插入基因片段
p1len += 1
if g not in tempGene:
newGene.append(g)
p1len += 1
return newGene
#获取下一代
def nextGen(self):
self.Gen+=1
#nextGen代表下一代的所有基因
nextGen=[]
#将最优秀的基因直接传递给下一代
nextGen.append(self.group.getBest().gene[:])
while(len(nextGen)<self.group.GroupSize):
pChange=random.random()
pCross=random.random()
p1=self.group.getOne()
if(pCross<self.pCross):
p2=self.group.getOne()
newGene=self.cross(p1,p2)
else:
newGene=p1.gene[:]
if(pChange<self.pChange):
newGene=self.change(newGene)
nextGen.append(newGene)
self.group.group=[]
for gene in nextGen:
self.group.group.append(Person(gene))
self.group.upDate()
#打印当前种群的最优个体信息
def showBest(self):
print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
#n代表代数,遗传算法的入口
def run(self,n):
Gen=[] #代数
dist=[] #每一代的最优距离
avgDist=[] #每一代的平均距离
#上面三个列表是为了画图
i=1
while(i<n):
self.nextGen()
self.showBest()
i+=1
Gen.append(i)
dist.append(1/self.group.getBest().fit)
avgDist.append(self.group.getAvg())
#绘制进化曲线
plt.plot(Gen,dist,'-r')
plt.plot(Gen,avgDist,'-b')
plt.show()
ga=GA()
ga.run(3000)
print("进行3000代后最优解:",1/ga.group.getBest().fit)Gambar di bawah ialah tangkapan skrin hasil percubaan Penyelesaian optimum ialah 11271

Untuk mengelakkan kontingensi eksperimen, eksperimen diulang 10 kali dan nilai purata dikira adalah seperti berikut.
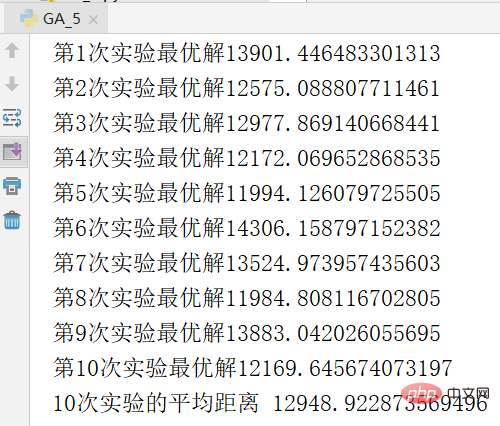
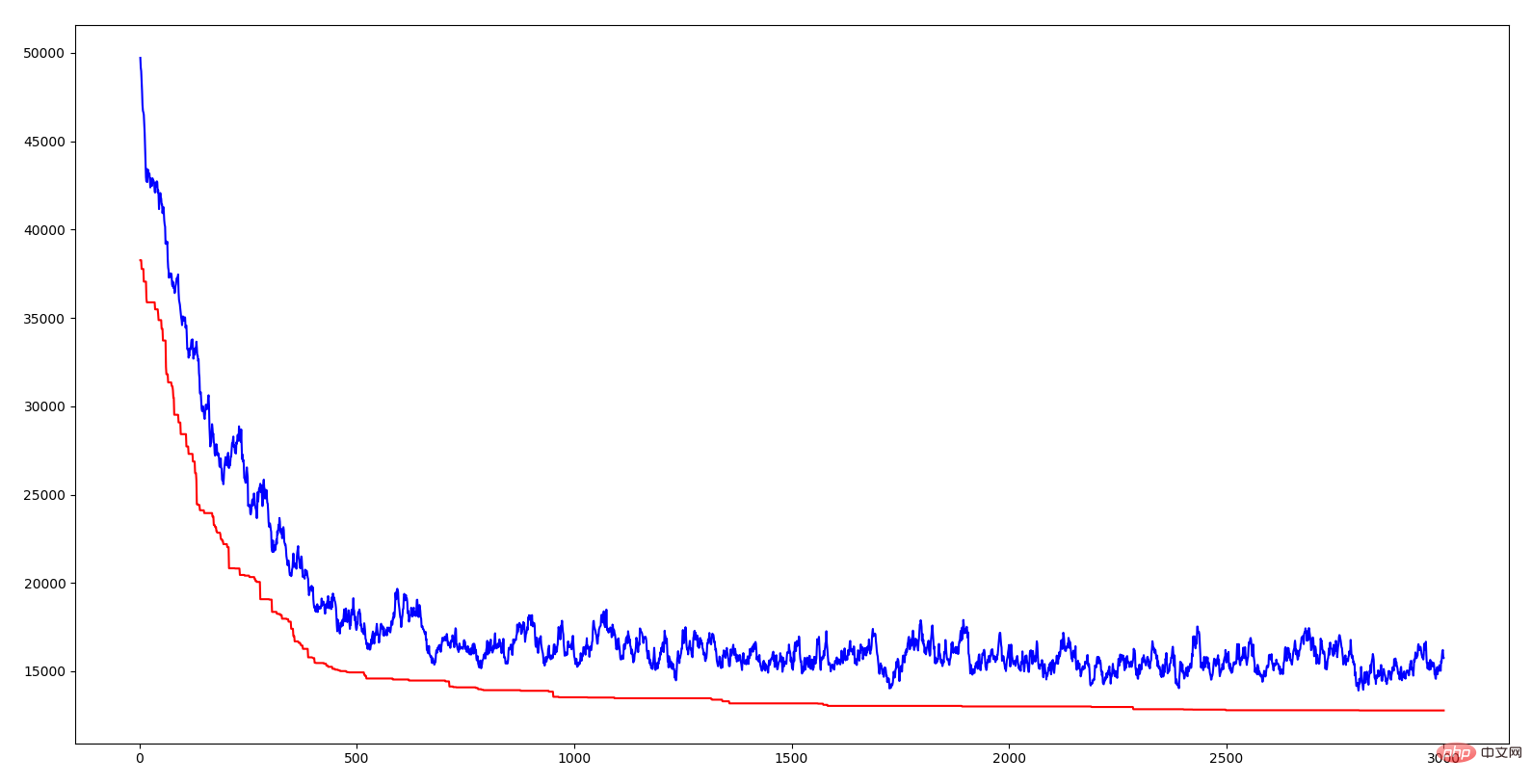
Absis rajah di atas ialah algebra, ordinat ialah jarak, lengkung merah ialah jarak individu optimum setiap generasi, dan biru Lengkung ialah jarak purata bagi setiap generasi. Ia boleh dilihat bahawa kedua-dua garisan menunjukkan arah aliran ke bawah, yang bermaksud ia sedang berkembang. Penurunan jarak purata menunjukkan bahawa disebabkan oleh kemunculan gen yang sangat baik (iaitu, urutan bandar tertentu), sifat yang sangat baik ini dengan cepat merebak ke seluruh penduduk. Sama seperti kelangsungan hidup yang paling cergas dalam alam semula jadi, hanya mereka yang mempunyai gen yang menyesuaikan diri dengan alam sekitar boleh bertahan Sejajar dengan itu, mereka yang bertahan adalah mereka yang mempunyai gen yang sangat baik. Kepentingan memperkenalkan kadar silang dan kadar mutasi dalam algoritma adalah untuk memastikan gen semasa yang sangat baik dan cuba menjana gen yang lebih baik. Jika semua individu menyeberang, beberapa segmen gen yang sangat baik mungkin hilang jika tidak ada yang menyeberang, maka dua segmen gen yang sangat baik tidak boleh digabungkan menjadi gen yang lebih baik, jika tidak ada variasi, individu yang lebih disesuaikan dengan persekitaran tidak dapat dihasilkan. Saya perlu mengeluh bahawa kebijaksanaan alam sangat berkuasa.
Serpihan gen yang disebutkan di atas ialah jujukan bandar pendek dalam TSP Apabila jumlah jarak bagi jujukan tertentu adalah agak kecil, ini bermakna jujukan ini merupakan susunan lintasan yang agak baik untuk bandar-bandar ini. Algoritma genetik mencapai pengoptimuman berterusan penyelesaian TSP dengan menggabungkan serpihan yang sangat baik ini. Kaedah gabungan menggunakan kebijaksanaan alam semula jadi, pewarisan, mutasi, dan kelangsungan hidup yang paling cergas.
Apa yang dipanggil survival of the fittest bermaksud pengekalan gen yang sangat baik dan penyingkiran gen yang tidak sesuai untuk persekitaran. Dalam algoritma GA di atas, saya menggunakan rolet, iaitu dalam langkah genetik (sama ada crossover atau tidak), setiap individu dipilih berdasarkan kecergasannya. Dengan cara ini, individu yang mempunyai kecergasan yang tinggi boleh mempunyai lebih ramai zuriat, sekali gus mencapai tujuan survival of the fittest.
Semasa proses pelaksanaan khusus, saya membuat kesilapan Apabila pada mulanya menyaring individu dalam langkah genetik, saya memadamkan individu ini daripada kumpulan setiap kali saya memilihnya. Difikirkan sekarang, pendekatan ini sangat bodoh Walaupun saya telah melaksanakan rolet pada masa itu, jika individu itu dipilih dan dipadamkan, ia akan menyebabkan setiap individu melahirkan zuriat yang sama untuk Membiarkan mereka yang mempunyai kecergasan tinggi diwarisi dahulu. Pendekatan ini benar-benar menyimpang daripada niat asal "survival of the fittest". Pendekatan yang betul ialah memilih individu untuk diwarisi dan kemudian meletakkan mereka kembali ke dalam populasi Ini boleh memastikan individu yang mempunyai kecergasan yang tinggi akan diwarisi berkali-kali, menghasilkan lebih banyak zuriat, dan menyebarkan gen yang cemerlang dengan lebih meluas akan Menghasilkan sedikit zuriat atau disingkirkan terus.
Apa yang dipanggil kemajuan ke hadapan bermakna individu optimum generasi akan datang mestilah lebih atau sama menyesuaikan diri dengan persekitaran berbanding generasi sebelumnya. Kaedah yang saya pakai ialah individu optimum terus memasuki generasi seterusnya tanpa mengambil bahagian dalam operasi seperti mutasi silang. Ini boleh menghalang evolusi terbalik daripada "mencemari" gen terbaik pada masa ini disebabkan oleh operasi ini.
Saya juga menghadapi masalah lain semasa proses pelaksanaan, sama ada ia disebabkan oleh lulus melalui rujukan atau nilai. Apabila menyeberangi dan memutasi gen individu, senarai digunakan Apabila melepasi senarai dalam Python, ia sebenarnya merupakan rujukan Ini akan menyebabkan gen individu itu diubah selepas menyilang dan memutasi individu. Hasilnya adalah evolusi yang sangat perlahan, disertai dengan evolusi terbalik.
Pilih serpihan satu individu dan masukkannya ke dalam individu lain, dan letakkan gen tidak pendua ke kedudukan lain mengikut urutan.
Apabila melaksanakan langkah ini, saya tersilap melaksanakan fungsi ini kerana pemahaman saya yang wujud tentang kelakuan kromosom sebenar semasa mempelajari biologi, "kromosom homolog menyeberang dan bertukar segmen homolog." Saya hanya menukar serpihan dua individu pada kedudukan yang sama untuk melengkapkan persilangan Jelas sekali pendekatan ini salah dan akan membawa kepada pertindihan bandar.
Semasa ujian berikutnya, saya mendapati sukar untuk menukar parameter dan mengemas kini maklumat individu, jadi saya menukar segala-galanya kepada OOP, yang menjadikannya lebih mudah. OOP menawarkan fleksibiliti dan kesederhanaan yang hebat untuk mensimulasikan masalah dunia sebenar seperti ini.
Semasa proses ujian, didapati penyelesaian optimum tempatan kadangkala muncul, yang tidak akan terus berkembang untuk jangka masa yang lama, dan penyelesaian pada masa ini jauh daripada penyelesaian optimum. Walaupun selepas pelarasan seterusnya, walaupun hampir dengan penyelesaian optimum, ia masih "optimum tempatan" kerana ia masih belum mencapai penyelesaian optimum.
Algoritma akan menumpu dengan cepat pada mulanya, tetapi akan menjadi lebih perlahan dan perlahan apabila ia berjalan, atau bahkan tidak bergerak langsung. Kerana pada peringkat akhir, semua individu mempunyai gen yang agak serupa, kesan silang pada evolusi pada masa ini sangat lemah, dan daya penggerak utama evolusi menjadi mutasi, dan mutasi adalah algoritma yang ganas. Jika anda bernasib baik, anda boleh berubah menjadi individu yang lebih baik dengan cepat, tetapi jika anda tidak bernasib baik, anda perlu menunggu.
Penyelesaian untuk menghalang penyelesaian optimum tempatan adalah dengan meningkatkan saiz populasi, supaya akan berlaku lebih banyak mutasi individu, dan akan ada kemungkinan yang lebih besar untuk menghasilkan individu yang berkembang. Kelemahan meningkatkan saiz populasi ialah masa pengiraan setiap generasi akan menjadi lebih lama, yang bermaksud bahawa kedua-duanya menghalang satu sama lain. Walaupun saiz populasi yang besar akhirnya boleh mengelakkan penyelesaian optimum tempatan, setiap generasi mengambil masa yang lama, dan ia mengambil masa yang lama untuk mencari penyelesaian optimum manakala saiz populasi yang lebih kecil, walaupun masa pengiraan setiap generasi adalah pantas, tidak akan menjadi diselesaikan selepas beberapa generasi akan jatuh ke dalam optimum tempatan.
Saya rasa kaedah pengoptimuman yang mungkin adalah menggunakan saiz populasi yang lebih kecil pada peringkat awal evolusi untuk mempercepatkan evolusi Apabila kecergasan mencapai ambang tertentu, tingkatkan saiz populasi dan kadar mutasi untuk mengelakkan maksima setempat Kemunculan penyelesaian unggul. Kaedah pelarasan dinamik ini digunakan untuk menimbang keseimbangan antara kecekapan pengkomputeran setiap generasi dan kecekapan pengkomputeran keseluruhan.
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan algoritma genetik menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




