

Rekursi sememangnya logik matematik yang agak abstrak, yang boleh difahami secara ringkas sebagai "program memanggil algoritmanya sendiri."
Penjelasan Wikipedia tentang rekursi ialah:
Rekursi (Bahasa Inggeris: Recursion), juga diterjemahkan sebagai rekursi, dalam matematik dan sains komputer, merujuk kepada penggunaan fungsi itu sendiri dalam definisi kaedah fungsi. Istilah rekursi juga lebih biasa digunakan untuk menggambarkan proses mengulangi perkara dengan cara yang serupa dengan diri sendiri.
Sebagai contoh, apabila dua cermin adalah lebih kurang selari antara satu sama lain, imej yang bersarang dalam cermin muncul dalam bentuk rekursi tak terhingga. Ia juga boleh difahami sebagai proses replikasi diri.
"Pas" bermaksud lulus, dan "Kembali" bermaksud kembalikan dahulu kaedah ke bawah lapisan demi lapisan, kemudian hantar ke lapisan terakhir dan kembalikan hasilnya.
Sebagai contoh, saya beratur untuk ujian asid nukleik, dan ada 100 orang di hadapan saya, saya ingin bertanya pukul berapa kakitangan perubatan akan keluar dari kerja , jadi saya bertanya kepada saudara di hadapan saya, dan dia bertanya lagi Orang di hadapannya menyampaikannya satu per satu, dan akhirnya menyampaikannya kepada kakitangan perubatan, yang menjawab bahawa mereka akan keluar dari kerja pada pukul 6 petang. Ayat ini dilepaskan dan akhirnya sampai kepada saya. Saya tahu bahawa kakitangan perubatan telah keluar dari kerja pada pukul enam.
Proses ini adalah proses rekursif Jika "melalui mesej" itu sendiri adalah kaedah, maka keseluruhan proses penghantaran mesej memanggil kaedahnya sendiri, dan akhirnya memperoleh hasilnya.
Ini berbeza daripada kitaran Kitaran ini sama dengan meletakkan fon kepala pada semua orang, dan kemudian "pengantara" akan bertanya kepada anda satu persatu jika anda tahu pukul berapa kakitangan perubatan akan keluar dari kerja tanya kakitangan perubatan,, dapat jawapan, "ejen" suruh saya keluar kerja pada pukul enam.
Pada asasnya, rekursi adalah untuk membongkar masalah besar secara berterusan, seperti mengupas bawang, dan akhirnya membongkarnya ke tahap terkecil, dan mengembalikan hasil penyelesaian.
Gunakan Python untuk memberikan contoh fungsi rekursif yang paling mudah dan bercakap tentang aplikasi rekursi.
Kami sering melihat fungsi memanggil diri mereka sendiri untuk melaksanakan operasi gelung, seperti fungsi untuk mencari faktorial.
Faktorial bagi integer n ialah n*(n-1)*(n-2)*...*3*2*1.
Sebagai contoh, 5 baris kod Python berikut boleh merealisasikan pengiraan faktorial.
def fact(n): ''' n表示要求的数的阶乘 ''' if n==1: return n n = n*fact(n-1) return n print(factorial(5))
Ramai orang mungkin keliru tentang logik pengiraan di sini, mengapa fungsi fakta memanggil dirinya sendiri dan akhirnya mendapat hasilnya.
Kita boleh menyimpulkannya mengikut logik matematik:
Faktorial bagi integer n ialah: fakta(n) = n*(n-1)*...*3*2* 1.
Faktorial bagi integer n-1 ialah: fakta(n-1) = (n-1)*(n-2)*...*3*2*1.
Jadi boleh disimpulkan bahawa fakta(n) = n*fakta(n-1).
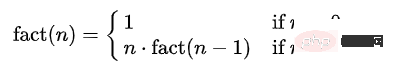
Adakah terdapat kaedah fakta yang boleh dipanggil untuk setiap nombor Apabila n=1 akhirnya dipanggil, faktorial hasil n dikembalikan.
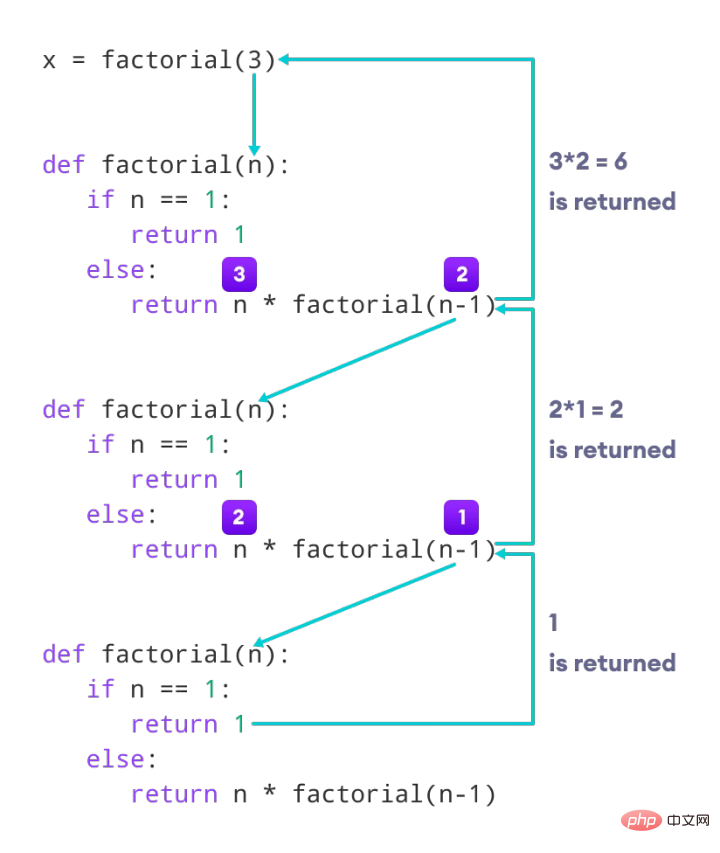
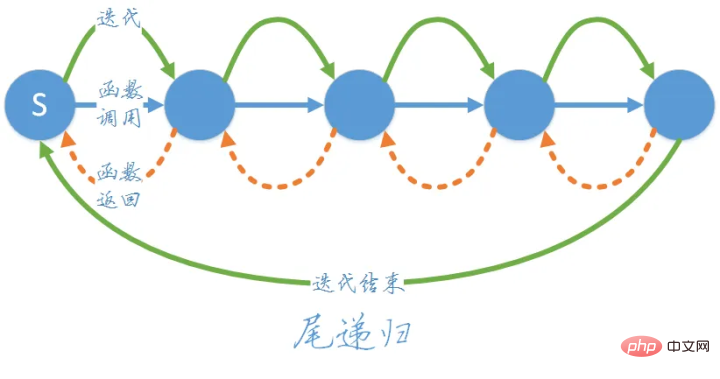
Lihat gambar di atas, fungsi rekursif akan dipanggil lapisan demi lapisan, dan akhirnya apabila n=1, hasilnya akan dikembalikan ke atas.
Ini adalah keseluruhan proses rekursi Jika kita memberikan definisi rekursi yang tepat, ia boleh diringkaskan sebagai tiga perkara berikut:
1 rekursi.
2. Berikan penyelesaian apabila rekursi tamat.
3. Setiap kali anda memasuki tahap rekursi yang lebih mendalam, saiz masalah (jumlah pengiraan) harus dikurangkan berbanding rekursi terakhir.
Ambil kod di atas sebagai contoh:
def factorial(n): ''' n表示要求的数的阶乘 ''' if n==1: # 1、明确递归终止条件; return n # 2、递归终止时的处理办法 n = n*factorial(n-1) # 递去 return n# 归来
Selain kes faktorial biasa, terdapat juga jujukan Fibonacci, yang juga merupakan penggunaan rekursi klasik.
Jujukan Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Jujukan ini bermula dari item 3, Setiap sebutan adalah sama kepada jumlah dua sebutan sebelumnya.
Ia ditakrifkan secara rekursif seperti berikut: F(0)=0, F(1)=1, F(n)=F(n - 1)+F(n - 2)( n≥2, n∈N*).
Dalam Python, kita boleh menggunakan fungsi rekursif untuk melaksanakan jujukan Fibonacci:
# 1,1,2,3,5,8,13,21,34,55,试判断数列第12个数是哪个? def fab(n): ''' n为斐波那契数列 ''' if n <= 2: v = 1 return v v = fab(n-1)+fab(n-2) return v print(fab(12))
Gunakan kaedah matematik untuk memperoleh:
Sebenarnya, kedua-dua kes rekursif di atas boleh dijelaskan melalui induksi matematik iaitu ilmu matematik sekolah menengah.
Secara amnya, untuk membuktikan proposisi P(n) berkaitan dengan nombor asli n, terdapat langkah-langkah berikut:
(1) Buktikan bahawa proposisi itu benar apabila n mengambil nilai pertama n0. n0 mengambil nilai 0 atau 1 untuk urutan umum, tetapi terdapat juga kes khas.
(2) Andaikan bahawa proposisi adalah benar apabila n=k (k≥n0, k ialah nombor asli), dan buktikan bahawa proposisi itu juga benar apabila n=k+1.
Mensintesis (1) (2), untuk semua nombor asli n (≥n0), proposisi P(n) adalah benar.
Selain penjelasan matematik, saya juga pernah melihat seseorang memberikan penjelasan yang lebih jelas tentang rekursi sebelum ini:
1、我们已经完成了吗?如果完成了,返回结果。如果没有这样的终止条件,递归将会永远地继续下去。
2、如果没有,则简化问题,解决较容易的问题,并将结果组装成原始问题的解决办法。然后返回该解决办法。
哈哈,到这里大家是不是对递归有了一个更加深刻的认识。
如果还不清楚,没关系,这里还有更多的递归案例,用Python来实现,可以说非常简洁。
def gcd(m, n): if n == 0: return m else: return gcd(n, m%n)
def sumnums(n): if n == 1: return 1 return n + sumnums(n - 1) print(sumnums(3))
def reverse(string): if len(string) == 0: return string else: return reverse(string[1:]) + string[0] reverseme = '我是帅哥' print(reverse(reverseme))
def towerOfHanoi(numrings, from_pole, to_pole, aux_pole):
if numrings == 1:
print('Move ring 1 from', from_pole, 'pole to', to_pole, 'pole')
return
towerOfHanoi(numrings - 1, from_pole, aux_pole, to_pole)
print('Move ring', numrings, 'from', from_pole, 'pole to', to_pole, 'pole')
towerOfHanoi(numrings - 1, aux_pole, to_pole, from_pole)
numrings = 2
towerOfHanoi(numrings, 'Left', 'Right', 'Middle')
data = [1,3,6,13,56,123,345,1024,3223,6688]
def dichotomy(min,max,d,n):
'''
min表示有序列表头部索引
max表示有序列表尾部索引
d表示有序列表
n表示需要寻找的元素
'''
mid = (min+max)//2
if mid==0:
return 'None'
elif d[mid]<n:
print('向右侧找!')
return dichotomy(mid,max,d,n)
elif d[mid]>n:
print('向左侧找!')
return dichotomy(min,mid,d,n)
else:
print('找到了%s'%d[mid])
return
res = dichotomy(0,len(data),data,222)
print(res)
有位大佬说过:To Iterate is Human, to Recurse, Divine。
中文译为:人理解迭代,神理解递归。
可见递归是非常神奇的算法,它的神奇之处在于它允许用户用有限的语句描述无限的对象。
当然人无完人,递归也是有缺点的,它一般效率较低,且会导致调用栈溢出。
因为递归不断调用自身函数,且产生大量变量,而栈空间的容量是有限的,循环太多就会效率低下,甚至导致调用栈溢出。
Atas ialah kandungan terperinci Bagaimana untuk lebih memahami algoritma rekursif? Penjelasan terperinci tentang contoh Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




