 Java
Java
 javaTutorial
javaTutorial
 Bagaimana untuk menggunakan timbunan untuk menyelesaikan masalah Top-k di Jawa?
Bagaimana untuk menggunakan timbunan untuk menyelesaikan masalah Top-k di Jawa?
Bagaimana untuk menggunakan timbunan untuk menyelesaikan masalah Top-k di Jawa?
1. Apakah timbunan?
Struktur timbunan
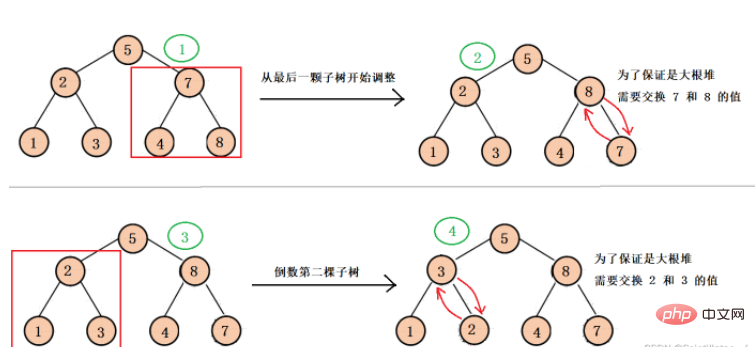
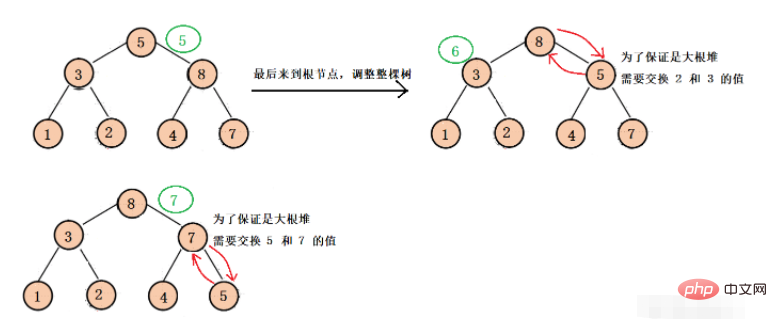
Timbunan sebenarnya adalah pokok binari, tetapi pokok binari biasa menyimpan data dalam struktur rantai, manakala timbunan menyimpan data secara berurutan dalam tatasusunan. Jadi apakah jenis pokok binari yang sesuai untuk penyimpanan berjujukan?
Kami mengandaikan bahawa pokok binari biasa boleh disimpan dalam tatasusunan, maka kami boleh mendapatkan struktur berikut:
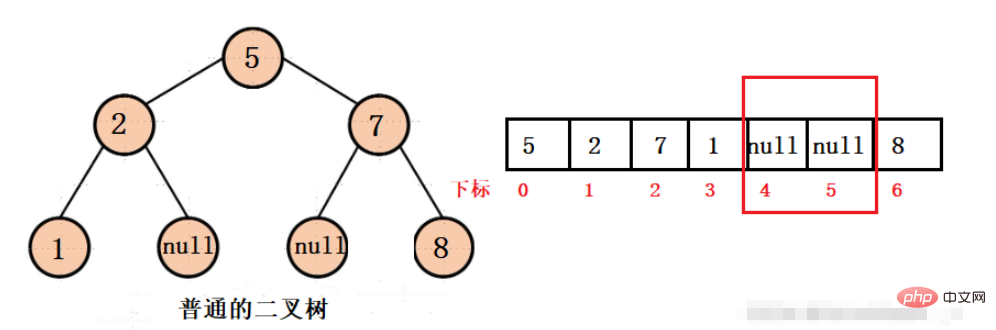
Kita dapat melihatnya apabila terdapat ruang di tengah-tengah nilai pokok binari, ruang penyimpanan tatasusunan akan terbuang, jadi dalam keadaan apakah ruang itu tidak akan dibazirkan? Itu adalah pokok binari yang lengkap.
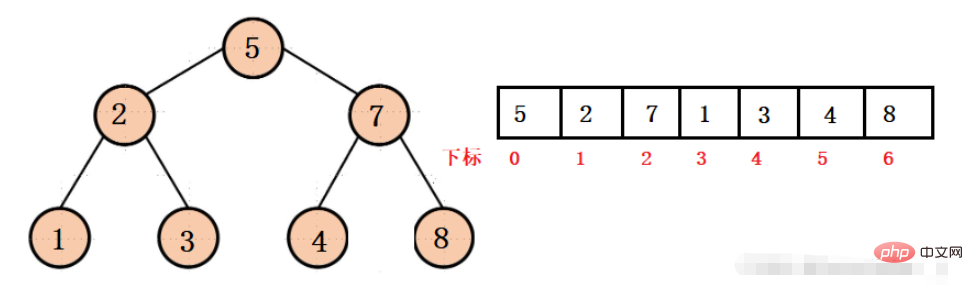
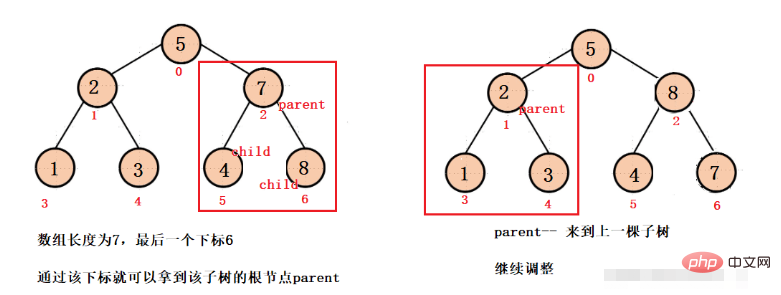
Daripada struktur di atas, kami tidak boleh menggunakan penunjuk struktur rantai untuk mengakses nod anak atau nod induk Kami hanya boleh mengaksesnya melalui subskrip yang sepadan, iaitu sebenarnya agak mudah.
Contohnya, dalam gambar di bawah:
Diketahui bahawa subskrip nod 2 ialah 1, kemudian
Subskrip anak kirinya ialah: 2 * 2 + 1 = 3
Subskrip anak kanannya ialah: 2 * 2 + 2 = 4
Sebaliknya, diketahui subskrip nod 1 ialah 3 dan subskrip bagi nod 3 ialah 4, kemudian
1 nod ialah: (3 - 1) / 2 = 1Subskrip nod induk bagi 3 nod ialah: (4 - 1) / 2 = 1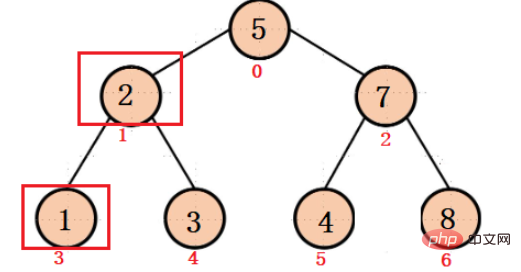
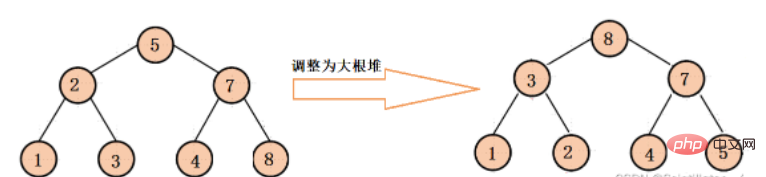
// 将数组变成大根堆结构
public void createHeap(int[] arr){
for (int i = 0; i < arr.length; i++) {
elem[i] = arr[i];// 放入elem[],假设不需要扩容
usedSize++;
}
// 得到根节点parent, parent--依次来到每颗子树的根节点,
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
// 依次向下搜索,使得每颗子树都变成大根堆
shiftDown(parent,usedSize);
}
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
int child = parent*2+1;// 拿到左孩子
while (child < len){
// 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较
if (child+1 < len && (elem[child] < elem[child+1])){
child++;
}
// 比较较大的孩子和父节点,看是否要交换
int max = elem[parent] >= elem[child] ? parent : child;
if (max == parent) break;// 如果不需要调整了,说明当前子树已经是大根堆了,直接 break
swap(elem,parent,child);
parent = child;// 继续向下检测,看是否要调整
child = parent*2+1;
}
}
public void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}Proses pelarasan adalah sama seperti di atas.
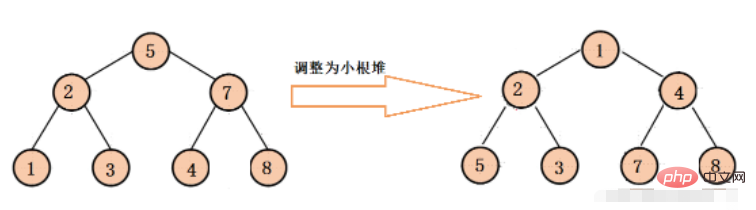
// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2,剩余最小的元素就是11,会被调整到堆顶,下一次弹出
System.out.println(smallHeap.poll());// 弹出11
// 如果需要得到大根堆,在里面传一个比较器
PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});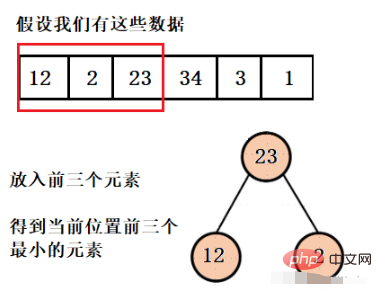
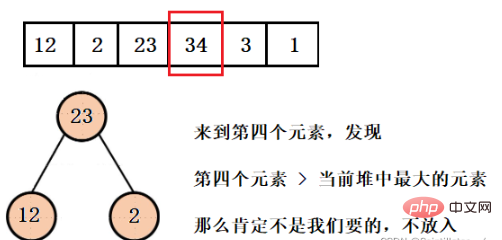
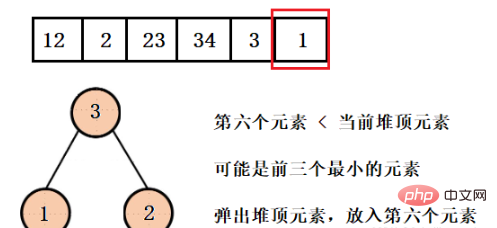
这样我们就得到了只含有前三个最小元素的堆,并且可以看到堆的大小一直都是3,而不是有多少数据就建多大的堆,然后再依次弹出元素就行了。
// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
// 创建一个大小为 k的大根堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
for (int i = 0; i < arr.length; i++) {
if (i < k){
// 放入前 k 个元素
maxHeap.offer(arr[i]);
}else{
// 从第 k+1个元素开始进行判断是否要入堆
if (maxHeap.peek() > arr[i]){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
}
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = maxHeap.poll();
}
return ret;
}Atas ialah kandungan terperinci Bagaimana untuk menggunakan timbunan untuk menyelesaikan masalah Top-k di Jawa?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1359
1359
 52
52
 Akar Kuasa Dua di Jawa
Aug 30, 2024 pm 04:26 PM
Akar Kuasa Dua di Jawa
Aug 30, 2024 pm 04:26 PM
Panduan untuk Square Root di Java. Di sini kita membincangkan cara Square Root berfungsi di Java dengan contoh dan pelaksanaan kodnya masing-masing.
 Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan Nombor Sempurna di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor Perfect dalam Java?, contoh dengan pelaksanaan kod.
 Penjana Nombor Rawak di Jawa
Aug 30, 2024 pm 04:27 PM
Penjana Nombor Rawak di Jawa
Aug 30, 2024 pm 04:27 PM
Panduan untuk Penjana Nombor Rawak di Jawa. Di sini kita membincangkan Fungsi dalam Java dengan contoh dan dua Penjana berbeza dengan contoh lain.
 Nombor Armstrong di Jawa
Aug 30, 2024 pm 04:26 PM
Nombor Armstrong di Jawa
Aug 30, 2024 pm 04:26 PM
Panduan untuk Nombor Armstrong di Jawa. Di sini kita membincangkan pengenalan kepada nombor Armstrong di java bersama-sama dengan beberapa kod.
 Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Weka di Jawa. Di sini kita membincangkan Pengenalan, cara menggunakan weka java, jenis platform, dan kelebihan dengan contoh.
 Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Nombor Smith di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor smith di Jawa? contoh dengan pelaksanaan kod.
 Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Dalam artikel ini, kami telah menyimpan Soalan Temuduga Spring Java yang paling banyak ditanya dengan jawapan terperinci mereka. Supaya anda boleh memecahkan temuduga.
 Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Java 8 memperkenalkan API Stream, menyediakan cara yang kuat dan ekspresif untuk memproses koleksi data. Walau bagaimanapun, soalan biasa apabila menggunakan aliran adalah: bagaimana untuk memecahkan atau kembali dari operasi foreach? Gelung tradisional membolehkan gangguan awal atau pulangan, tetapi kaedah Foreach Stream tidak menyokong secara langsung kaedah ini. Artikel ini akan menerangkan sebab -sebab dan meneroka kaedah alternatif untuk melaksanakan penamatan pramatang dalam sistem pemprosesan aliran. Bacaan Lanjut: Penambahbaikan API Java Stream Memahami aliran aliran Kaedah Foreach adalah operasi terminal yang melakukan satu operasi pada setiap elemen dalam aliran. Niat reka bentuknya adalah



