
Sebelum mempelajari algoritma bahagi dan takluk, izinkan saya bertanyakan soalan kepada anda Jika ibu bapa dan saudara-mara anda memberi wang, anda akan memasukkannya ke dalam harta anda sendiri. Tetapi anda mungkin merasa rumit untuk mengendalikan longgokan wang, kerana datanya agak besar berbanding dengan otak anda, dan mudah untuk membuat kesilapan Anda boleh membahagikannya kepada beberapa bahagian kecil dan kemudian menambahnya untuk mengira jumlahnya . Jumlah keseluruhan wang ini adalah
Sudah tentu, jika anda rasa jumlah wang dalam setiap bahagian masih terlalu besar, anda masih boleh membahagikan dan menggabungkannya. . Sebab mengapa kita mempunyai begitu banyak ialah:
Cara mengira setiap longgokan wang yang kecil adalah sama dengan cara mengira longgokan wang yang paling besar (perbezaannya terletak pada saiz)
Maka yang besar Jumlah timbunan wang sebenarnya adalah jumlah hasil daripada timbunan wang yang kecil. Dengan cara ini, sebenarnya terdapat mentaliti divide and conquer.
Algoritma bahagi dan takluk ialah algoritma yang menggunakan idea bahagi dan takluk menakluki?
Bahagi dan takluk, secara literal bermaksud "bahagi dan takluk", iaitu membahagikan masalah yang kompleks kepada dua atau lebih sub-masalah yang serupa atau serupa, dan kemudian membahagikan sub-masalah kepada sub-masalah yang lebih kecil.. .…Sehingga akhir, sub-masalah boleh diselesaikan secara ringkas dan langsung, dan penyelesaian kepada masalah asal ialah gabungan penyelesaian kepada sub-masalah. Dalam sains komputer, kaedah divide-and-conquer merupakan algoritma yang sangat penting yang menggunakan idea divide-and-conquer. Kaedah bahagi-dan-takluk adalah asas kepada banyak algoritma yang cekap, seperti algoritma pengisihan (isih cepat, isihan gabungan), transformasi Fourier (transformasi Fourier cepat), dsb.
Uraikan masalah induk kepada sub-masalah dan selesaikan dengan cara yang sama Ini konsisten dengan konsep rekursi, jadi algoritma bahagi-dan-takluk biasanya dilaksanakan dengan cara rekursif (sudah tentu ada. juga merupakan pelaksanaan bukan rekursif).
Perihalan algoritma bahagi-dan-takluk mudah difahami secara literal, Bahagi dan takluk sebenarnya melibatkan proses penggabungan:
<.>Bahagi: Selesaikan masalah yang lebih kecil secara rekursif (berhenti apabila mencapai lapisan penamatan atau apabila ia boleh diselesaikan)
Takluk: Selesaikan secara rekursif, atau selesaikan secara langsung jika masalahnya cukup kecil.
Gabungkan: Bina penyelesaian sub-masalah menjadi masalah induk
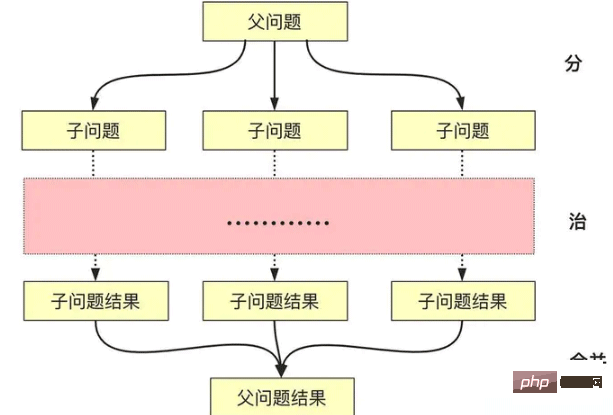
Jadi apakah syarat (ciri) yang perlu dipenuhi untuk masalah diselesaikan menggunakan algoritma bahagi-dan-takluk?
public int searchInsert(int[] nums, int target) {
if(nums[0]>=target)return 0;//剪枝
if(nums[nums.length-1]==target)return nums.length-1;//剪枝
if(nums[nums.length-1]<target)return nums.length;
int left=0,right=nums.length-1;
while (left<right) {
int mid=(left+right)/2;
if(nums[mid]==target)
return mid;
else if (nums[mid]>target) {
right=mid;
}
else {
left=mid+1;
}
}
return left;
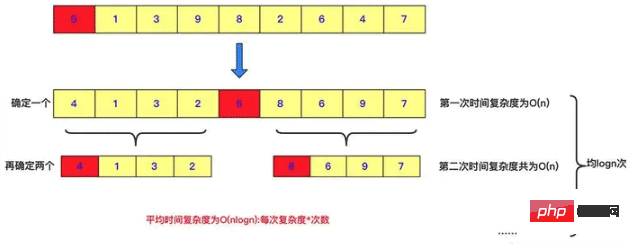
}Isih cepat juga merupakan contoh bahagi dan takluk Setiap hantaran cepat akan memilih nombor, dan meletakkan nombor yang lebih kecil di sebelah kiri, dan nombor yang lebih besar di sebelah kiri. Letakkannya di sebelah kanan, dan kemudian bahagikan dan takluk secara rekursif untuk menyelesaikan dua sub-selang Sudah tentu, isihan cepat telah melakukan banyak kerja apabila semua bahagian diisih ke bawah, nilainya daripada jujukan ini ialah nilai yang disusun. Ini adalah manifestasi perpecahan dan penaklukan.
public void quicksort(int [] a,int left,int right)
{
int low=left;
int high=right;
//下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!!
if(low>high)//作为判断是否截止条件
return;
int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。
while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
{
while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
{
high--;
}
//这样就找到第一个比它小的了
a[low]=a[high];//放到low位置
while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置
{
low++;
}
a[high]=a[low];
}
a[low]=k;//赋值然后左右递归分治求之
quicksort(a, left, low-1);
quicksort(a, low+1, right);
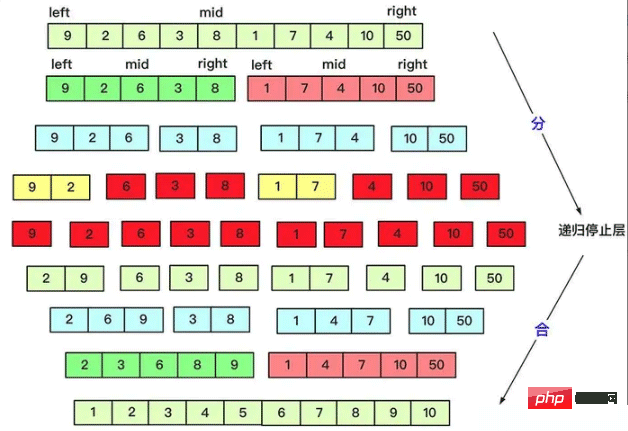
}Isih cepat melakukan banyak kerja apabila membahagi, tetapi penggabungan adalah sebaliknya , bahagikannya sama rata mengikut kuantiti, dan apabila digabungkan, ia sudah digabungkan dengan teratur, kerana hasil yang diperlukan boleh diperolehi dengan kerumitan tahap O(n) bagi dua urutan tertib. Ubah bentuk nombor ordinal terbalik berdasarkan pengisihan gabungan juga diselesaikan dengan idea bahagi dan takluk.
private static void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;
if(left<right)
{
mergesort(array, left, mid);
mergesort(array, mid+1, right);
merge(array, left,mid, right);
}
}
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {//先左右比较合并
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
}
}
while(lindex<=mid)//当一个越界后剩余按序列添加即可
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
}jumlah susulan maksimum, kita boleh menggunakan pengaturcaraan dinamik untuk menyelesaikan masalah, tetapi kita boleh. juga menggunakan algoritma bahagi dan takluk untuk menyelesaikan masalah, tetapi jumlah susulan maksimum bukanlah gabungan mudah apabila digabungkan, kerana jumlah susulan melibatkan isu panjang, jadi hasil yang betul mungkin tidak semuanya berada di sebelah kiri atau paling kanan, dan keputusan mungkin berlaku Kawasannya ialah:
sepenuhnya di sebelah kiri tengah
sepenuhnya di sebelah kanan tengah
Jujukan yang mengandungi nod kiri dan kanan di tengah
boleh diwakili oleh graf:
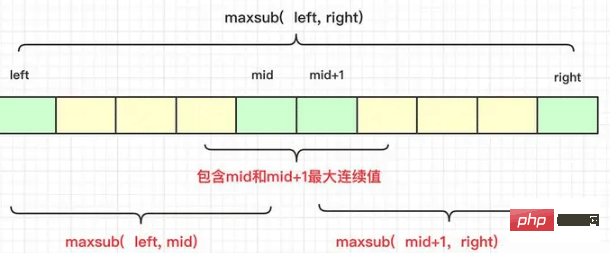
Oleh itu, apabila mempertimbangkannya secara khusus, adalah perlu untuk mengira hasil rentetan nilai maksimum di tengah yang tidak boleh diperoleh secara rekursif, dan mengambil bahagian dalam perbandingan antara sisi kiri dan kanan.
Kod yang dilaksanakan mengikut jumlah susulan maksimum ialah:
public int maxSubArray(int[] nums) {
int max=maxsub(nums,0,nums.length-1);
return max;
}
int maxsub(int nums[],int left,int right)
{
if(left==right)
return nums[left];
int mid=(left+right)/2;
int leftmax=maxsub(nums,left,mid);//左侧最大
int rightmax=maxsub(nums,mid+1,right);//右侧最大
int midleft=nums[mid];//中间往左
int midright=nums[mid+1];//中间往右
int team=0;
for(int i=mid;i>=left;i--)
{
team+=nums[i];
if(team>midleft)
midleft=team;
}
team=0;
for(int i=mid+1;i<=right;i++)
{
team+=nums[i];
if(team>midright)
midright=team;
}
int max=midleft+midright;//中间的最大值
if(max<leftmax)
max=leftmax;
if(max<rightmax)
max=rightmax;
return max;
}Pasangan titik terdekat ialah bahagi dan. conquer very Salah satu aplikasi yang berjaya. Terdapat beberapa koordinat titik pada paksi koordinat dua dimensi, membolehkan anda mencari jarak antara dua titik terdekat Jika anda diminta mencarinya secara langsung, keganasan penghitungan adalah jumlah pengiraan yang sangat besar kaedah bahagi dan takluk untuk mengoptimumkan Masalah seperti ini.
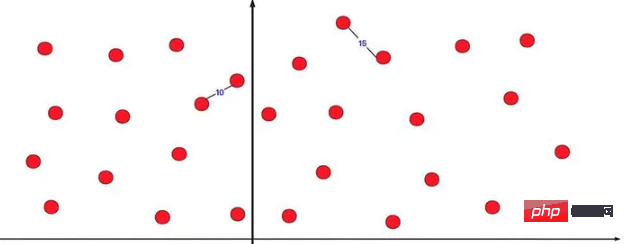
Jika anda terus membahagikannya kepada dua bahagian dan mengira bahagi dan menakluk, anda pasti akan mendapati bahawa jika yang paling pendek ialah satu di sebelah kiri dan satu di sebelah kanan, akan ada masalah. Kita boleh mengoptimumkannya.
Dalam pelan pengoptimuman khusus, pertimbangkan dimensi x atau y, bahagikan data kepada dua kawasan dan mula-mula hitung (mengikut kaedah yang sama) pasangan titik terpendek di kawasan kiri dan kanan masing-masing. Kemudian tutupnya ke kiri dan kanan mengikut jarak yang lebih pendek antara keduanya, kira jarak antara titik kiri dan kanan yang dilindungi, cari jarak terkecil dan bandingkan dengan jarak terpendek semasa.
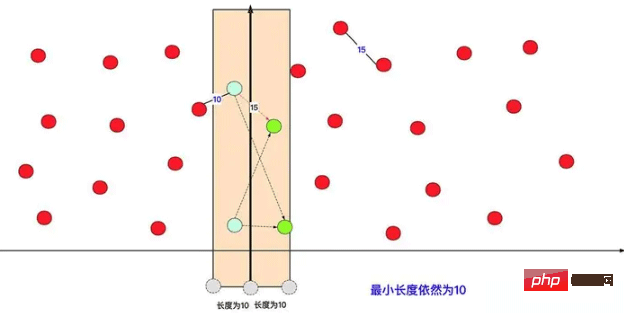
Dengan cara ini, anda boleh mendapati bahawa dengan operasi yang satu ini (tanpa mengira sub-kes), titik merah di sebelah kiri mengelakkan pengiraan jarak dengan kebanyakan titik merah di sebelah kanan (O (kerumitan masa n2)). Malah, apabila melakukan pengiraan dalaman dalam selang kiri dan kanan, ia sebenarnya melakukan banyak pengiraan bahagi-dan-takluk secara rekursif. Seperti yang ditunjukkan dalam gambar:
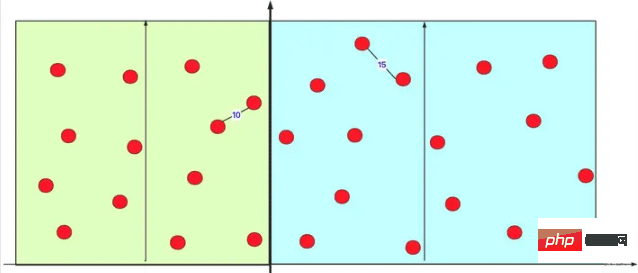
Dengan cara ini anda boleh menjimatkan banyak pengiraan.
Walau bagaimanapun, terdapat masalah dengan pembahagian dan penaklukan jenis ini Koordinat dua dimensi mungkin mempunyai titik berkelompok pada kaedah tertentu dan paksi tertentu, jadi kesannya mungkin tidak jelas (matanya semuanya. berhampiran x=2 dan tidak mempunyai kesan pada pembahagian x besar), anda perlu memperhatikannya. Kod untuk
ac ialah:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
public class Main {
static int n;
public static void main(String[] args) throws IOException {
StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
//List<node>list=new ArrayList();
while(in.nextToken()!=StreamTokenizer.TT_EOF)
{
n=(int)in.nval;if(n==0) {break;}
node no[]=new node[n];
for(int i=0;i<n;i++)
{
in.nextToken();double x=in.nval;
in.nextToken();double y=in.nval;
// list.add(new node(x,y));
no[i]=new node(x,y);
}
Arrays.sort(no, com);
double min= search(no,0,n-1);
out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush();
}
}
private static double search(node[] no, int left,int right) {
int mid=(right+left)/2;
double minleng=0;
if(left==right) {return Double.MAX_VALUE;}
else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);}
else minleng= min(search(no,left,mid),search(no,mid,right));
int ll=mid;int rr=mid+1;
while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;}
while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;}
for(int i=ll;i<rr;i++)
{
for(int j=i+1;j<rr+1;j++)
{
double team=0;
if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;}
else
{
team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y);
if(team<minleng)minleng=team;
}
}
}
return minleng;
}
private static double min(double a, double b) {
// TODO 自动生成的方法存根
return a<b?a:b;
}
static Comparator<node>com=new Comparator<node>() {
@Override
public int compare(node a1, node a2) {
// TODO 自动生成的方法存根
return a1.y-a2.y>0?1:-1;
}};
static class node
{
double x;
double y;
public node(double x,double y)
{
this.x=x;
this.y=y;
}
}
}Atas ialah kandungan terperinci Reka bentuk dan analisis algoritma Java: penjelasan terperinci tentang contoh algoritma divide-and-conquer. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




