Langkah dan pelaksanaan algoritma pengisihan Timsort di Jawa

Latar Belakang

Timsort ialah algoritma pengisihan hibrid dan stabil, ia adalah gabungan algoritma Isih Gabungan dan Isih Sisipan Binari sebagai algoritma pengisihan terbaik di dunia. Timsort sentiasa menjadi algoritma pengisihan standard Python. API Timsort telah ditambah selepas Java SE 7. Kita dapat melihat daripada Arrays.sort bahawa ia sudah menjadi algoritma pengisihan lalai untuk tatasusunan jenis bukan primitif. Jadi sama ada pembelajaran pengaturcaraan lanjutan atau temu bual, adalah lebih penting untuk memahami Timsort.

// List sort()    
default void sort(Comparator<? super E> c) {
        Object[] a = this.toArray();
              //数组排序
        Arrays.sort(a, (Comparator) c);
              ...
    }

// Arrays.sort
    public static <T> void sort(T[] a, Comparator<? super T> c) {
        if (c == null) {
            sort(a);
        } else {
              // 废弃版本
            if (LegacyMergeSort.userRequested)
                legacyMergeSort(a, c);
            else
                TimSort.sort(a, 0, a.length, c, null, 0, 0);
        }
    }

    public static void sort(Object[] a) {
        if (LegacyMergeSort.userRequested)
            legacyMergeSort(a);
        else
            ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
    }

Pengetahuan prasyarat

Untuk memahami Timsort, anda perlu menyemak pengetahuan berikut terlebih dahulu.

Carian Eksponen

Carian eksponen, juga dikenali sebagai carian berganda, ialah algoritma yang dicipta untuk mencari elemen dalam tatasusunan besar. Ia adalah proses dua langkah. Pertama, algoritma cuba mencari julat (L，R) di mana unsur sasaran wujud, dan kemudian menggunakan carian binari dalam julat ini untuk mencari lokasi sebenar sasaran. Kerumitan masa ialah O(lgn). Algoritma carian ini berkesan dalam tatasusunan tertib yang besar.

Isih Sisipan Perduaan

Algoritma isihan sisipan adalah sangat mudah Proses umum adalah bermula dari elemen kedua dan bergerak ke hadapan dan menukar elemen sehingga kedudukan yang sesuai ditemui.

Kerumitan masa optimum bagi isihan sisipan juga ialah O(n) Kita boleh menggunakan carian binari untuk mengurangkan bilangan perbandingan elemen semasa pemasukan dan mengurangkan kerumitan masa log masuk . Walau bagaimanapun, ambil perhatian bahawa isihan sisipan carian binari masih memerlukan pengalihan bilangan elemen yang sama, tetapi penggunaan masa untuk menyalin tatasusunan adalah lebih rendah daripada operasi swap satu demi satu.

Ciri: Kelebihan utama isihan sisipan binari ialah ia sangat cekap dalam senario set data kecil.

public static int[] sort(int[] arr) throws Exception {
        // 开始遍历第一个元素后的所有元素
        for (int i = 1; i < arr.length; i++) {
            // 需要插入的元素
            int tmp = arr[i];
            // 从已排序最后一个元素开始，如果当前元素比插入元素大，就往后移动
            int j = i;
            while (j > 0 && tmp < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }
            // 将元素插入
            if (j != i) {
                arr[j] = tmp;
            }
        }
        return arr;
    }

    public static int[] binarySort(int[] arr) throws Exception {
        for (int i = 1; i < arr.length; i++) {
            // 需要插入的元素
            int tmp = arr[i];
            // 通过二分查找直接找到插入位置
            int j = Math.abs(Arrays.binarySearch(arr, 0, i, tmp) + 1);
            // 找到插入位置后，通过数组复制向后移动，腾出元素位置
            System.arraycopy(arr, j, arr, j + 1, i - j);
            // 将元素插入
            arr[j] = tmp;
        }
        return arr;
    }

Isih Gabung

Isih Gabung ialah algoritma yang menggunakan strategi bahagi-dan-takluk dan mengandungi dua operasi utama: Split dan Gabung. Proses umum ialah membahagikan tatasusunan secara rekursif kepada dua bahagian sehingga ia tidak boleh dibahagikan lagi (iaitu tatasusunan kosong atau hanya mempunyai satu elemen sahaja yang tinggal), dan kemudian bergabung dan mengisih. Ringkasnya, operasi cantum adalah untuk terus mengambil dua tatasusunan tersusun yang lebih kecil dan menggabungkannya menjadi tatasusunan yang lebih besar.

Ciri-ciri: Isih Gabungan terutamanya algoritma pengisihan yang direka untuk senario set data yang besar.

public static void mergeSortRecursive(int[] arr, int[] result, int start, int end) {
        // 跳出递归
        if (start >= end) {
            return;
        }
        // 待分割的数组长度
        int len = end - start;
        int mid = (len >> 1) + start;
        int left = start; // 左子数组开始索引
        int right = mid + 1; // 右子数组开始索引
        // 递归切割左子数组，直到只有一个元素
        mergeSortRecursive(arr, result, left, mid);
        // 递归切割右子数组，直到只有一个元素
        mergeSortRecursive(arr, result, right, end);
        int k = start;
        while (left <= mid && right <= end) {
            result[k++] = arr[left] < arr[right] ? arr[left++] : arr[right++];
        }
        while (left <= mid) {
            result[k++] = arr[left++];
        }
        while (right <= end) {
            result[k++] = arr[right++];
        }
        for (k = start; k <= end; k++) {
            arr[k] = result[k];
        }
    }

    public static int[] merge_sort(int[] arr) {
        int len = arr.length;
        int[] result = new int[len];
        mergeSortRecursive(arr, result, 0, len - 1);
        return arr;
    }

Proses pelaksanaan Timsort

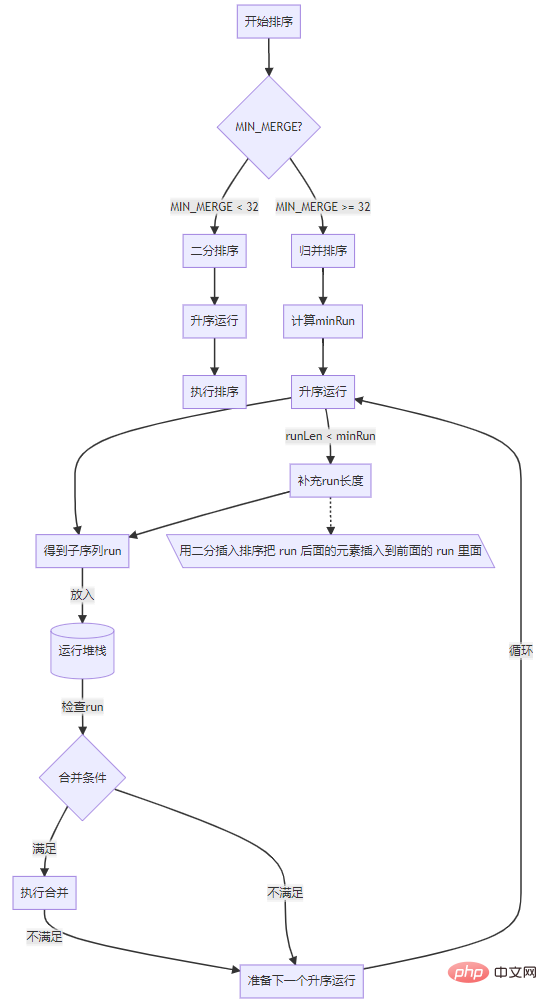
Proses umum algoritma, jika panjang tatasusunan kurang daripada ambang yang ditentukan (MIN_MERGE ) Gunakan terus algoritma sisipan binari untuk melengkapkan pengisihan, jika tidak lakukan langkah berikut:

• Mulakan dari sebelah kiri tatasusunan, laksanakan jalankan dalam tertib menaik untuk mendapatkan susulan .

• Letakkan ini urutan ke dalam tindanan yang sedang berjalan dan tunggu untuk melaksanakan cantuman.

• Semak urutan dalam tindanan yang sedang berjalan, dan laksanakan cantuman jika syarat penggabungan dipenuhi.

• Ulang langkah pertama dan lakukan lari menaik seterusnya seterusnya.

Operasi tertib menaik

Operasi tertib menaik ialah proses mencari turutan meningkat (tertib menaik) atau menurun (tertib menurun) berterusan daripada tatasusunan. Jika jujukan Jika jujukan dalam tertib menurun, balikkan kepada tertib menaik Proses ini juga boleh dipendekkan kepada run. Contohnya, dalam tatasusunan [2,3,6,4,9,30], anda boleh menemui tiga jujukan, [2,3,6], [4,9], [30] atau 3 run.

Beberapa ambang utama

MIN_MERGE

Ini ialah nilai malar, yang boleh difahami secara ringkas sebagai ambang minimum untuk melaksanakan penggabungan panjang tatasusunan Jika ia lebih kecil daripadanya, tidak perlu melakukan pengisihan yang begitu rumit, hanya sisipan binari. Dalam pelaksanaan C Tim Peter, ia adalah 64, tetapi dalam pengalaman sebenar, menetapkannya kepada 32 berfungsi lebih baik, jadi nilai dalam java ialah 32.

Untuk memastikan kestabilan semasa membalikkan tertib menurun, elemen yang sama tidak akan diterbalikkan.

minrun

Apabila menggabungkan jujukan, jika bilangan run bersamaan atau kurang sedikit daripada kuasa 2, kecekapan penggabungan ialah tertinggi; jika lebih besar sedikit daripada kuasa 2, kecekapan akan berkurangan dengan ketara. Oleh itu, untuk meningkatkan kecekapan penggabungan, adalah perlu untuk mengawal panjang setiap run sebanyak mungkin Dengan menentukan minrun untuk mewakili panjang minimum setiap run, jika. panjangnya terlalu pendek, gunakan isihan sisipan binari untuk mengisih < Elemen berikut 🎜> dimasukkan ke dalam run sebelumnya. run

Secara amnya, sebelum melaksanakan algoritma pengisihan, minrun ini akan dikira terlebih dahulu (ia melaraskan dirinya mengikut ciri-ciri data akan memilih nombor dari 32 hingga 64, jadi saiz data dibahagikan). oleh minrun adalah sama dengan Atau kurang sedikit daripada kuasa 2. Contohnya, jika panjangnya ialah 65, maka nilai minrun ialah 33; jika panjangnya ialah 165, nilai minrun ialah 42;

看下 Java 里面的实现，如果数据长度（n） < MIN_MERGE，则返回数据长度。如果数据长度恰好是 2 的幂次方，则返回MIN_MERGE/2
也就是16，否则返回一个MIN_MERGE/2 <= k <= MIN_MERGE范围的值k，这样可以使的 n/k 接近但严格小于 2 的幂次方。

private static int minRunLength(int n) {
        assert n >= 0;
        int r = 0;      // 如果低位任何一位是1，就会变成1
        while (n >= MIN_MERGE) {
            r |= (n & 1);
            n >>= 1;
        }
        return n + r;
    }

MIN_GALLOP

MIN_GALLOP 是为了优化合并的过程设定的一个阈值，控制进入 GALLOP 模式中， GALLOP 模式放在后面讲。

下面是 Timsort 执行流程图

运行合并

当栈里面的 run 满足合并条件时，它就将栈里面相邻的两个run 进行合并。

合并条件

Timsort 为了执行平衡合并（让合并的 run 大小尽可能相同），制定了一个合并规则，对于在栈顶的三个run，分别用X、Y 和 Z 表示他们的长度，其中 X 在栈顶，它们必须始终维持一下的两个规则：

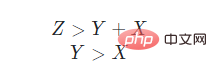
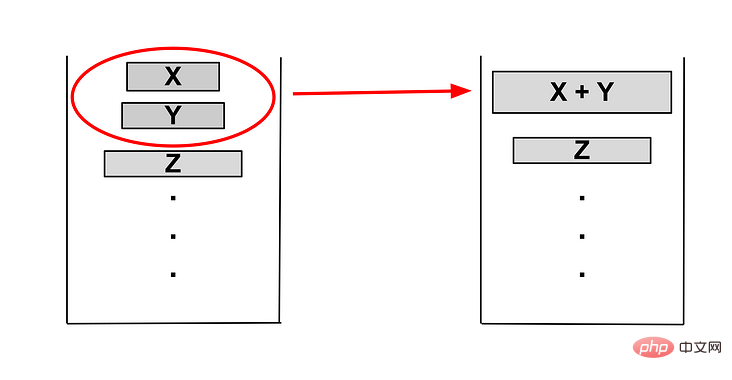
一旦有其中的一个条件不被满足，则将 Y 与 X 或 Z 中的较小者合并生成新的 run，并再次检查栈顶是否仍然满足条件。如果不满足则会继续进行合并，直至栈顶的三个元素都满足这两个条件，如果只剩两个run，则满足 Y > X 即可。

如下下图例子

• 当 Z <= Y+X ，将 X+Y 合并，此时只剩下两个run。

• 检测 Y < X ，执行合并，此时只剩下 X，则退出合并检测。

我们看下 Java 里面的合并实现

private void mergeCollapse() {
      
       // 当存在两个以上run执行合并检查
        while (stackSize > 1) {

          // 表示 Y
            int n = stackSize - 2; 
           
          // Z <= Y + X 
            if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) { 

              // 如果 Z < X 合并Z+Y ，否则合并X+Y
              if (runLen[n - 1] < runLen[n + 1])
                    n--;
                
                // 合并相邻的两个run，也就是runLen[n] 和 runLen[n+1]
                mergeAt(n); 
            } else if (runLen[n] <= runLen[n + 1]) {
                
                // Y <= X 合并 Y+X
                mergeAt(n);
            } else {
                
                // 满足两个条件，跳出循环
                break; 
            }
        }
    }

合并内存开销

原始归并排序空间复杂度是 O(n)也就是数据大小。为了实现中间项，Timsort 进行了一次归并排序，时间开销和空间开销都比 O(n)小。

优化是为了尽可能减少数据移动，占用更少的临时内存，先找出需要移动的元素，然后将较小序列复制到临时内存，在按最终顺序排序并填充到组合序列中。

比如我们需要合并 X [1, 2, 3, 6, 10] 和 Y [4, 5, 7, 9, 12, 14, 17]，X 中最大元素是10，我们可以通过二分查找确定，它需要插入到 Y 的第 5个位置才能保证顺序，而 Y 中最小元素是4，它需要插入到 X 中的第4个位置才能保证顺序，那么就知道了[1, 2, 3] 和 [12, 14, 17] 不需要移动，我们只需要移动 [6, 10] 和 [4, 5, 7, 9]，然后只需要分配一个大小为 2 临时存储就可以了。

合并优化

在归并排序算法中合并两个数组需要一一比较每个元素，为了优化合并的过程，设定了一个阈值 MIN_GALLOP，当B中元素向A合并时，如果A中连续 MIN_GALLOP 个元素比B中某一个元素要小，那么就进入GALLOP模式。

根据基准测试，比如当A中连续7个以上元素比B中某一元素小时切入该模式效果才好，所以初始值为7。

当进入GALLOP模式后，搜索算法变为指数搜索，分为两个步骤，比如想确定 A 中元素x在 B 中确定的位置

• 首先在 B 中找到合适的索引区间(2^k−1,2^k+1−1) 使得 x 元素在这个范围内；

• 然后在第一步找到的范围内通过二分搜索来找到对应的位置。

只有当一次运行的初始元素不是另一次运行的前七个元素之一时，驰骋才是有益的。这意味着初始阈值为 7。

Atas ialah kandungan terperinci Langkah dan pelaksanaan algoritma pengisihan Timsort di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!