 Peranti teknologi
Peranti teknologi
 AI
AI
 Bandingkan kaedah ramalan siri masa berdasarkan SARIMA, XGBoost dan CNN-LSTM.
Bandingkan kaedah ramalan siri masa berdasarkan SARIMA, XGBoost dan CNN-LSTM.
Bandingkan kaedah ramalan siri masa berdasarkan SARIMA, XGBoost dan CNN-LSTM.
Pengujian prestasi dan perbandingan menganalisis dan meramal penjanaan tenaga suria menggunakan ujian statistik dan pembelajaran mesin
Artikel ini akan membincangkan teknik untuk memperoleh nilai ketara daripada set data melalui penggunaan ujian hipotesis, kejuruteraan ciri, siri masa kaedah pemodelan, dsb. Saya juga akan menangani isu seperti kebocoran data dan penyediaan data untuk model siri masa yang berbeza, dan menjalankan ujian perbandingan tiga ramalan siri masa biasa.
Pengenalan
Ramalan siri masa ialah topik yang kerap dikaji Di sini kami menggunakan data dua loji tenaga solar untuk mengkaji undang-undangnya dan menjalankan pemodelan. Selesaikan isu ini dengan terlebih dahulu menguraikannya menjadi dua soalan:
- Adakah mungkin untuk mengenal pasti modul solar yang kurang berprestasi?
- Adakah mungkin untuk meramalkan penjanaan tenaga suria selama dua hari?
Sebelum kita terus menjawab soalan-soalan ini, mari kita fahami dahulu bagaimana loji kuasa solar menjana tenaga elektrik.
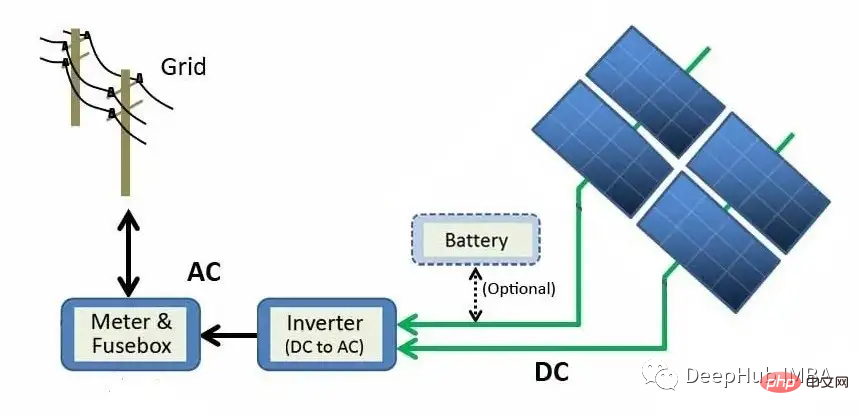
Rajah di atas menerangkan proses penjanaan daripada modul panel solar ke grid. Tenaga suria ditukar terus kepada tenaga elektrik melalui kesan fotoelektrik. Apabila bahan seperti silikon (bahan semikonduktor yang paling biasa dalam panel solar) terdedah kepada cahaya, foton (zarah subatom tenaga elektromagnet) diserap dan elektron bebas dibebaskan, menghasilkan arus terus (DC). Menggunakan penyongsang, kuasa DC ditukar kepada arus ulang alik (AC) dan dihantar ke grid, di mana ia boleh diagihkan ke rumah.
Data
Data mentah terdiri daripada dua fail nilai dipisahkan koma (CSV) untuk setiap loji tenaga solar. Satu dokumen menunjukkan proses penjanaan kuasa dan satu lagi menunjukkan ukuran yang direkodkan oleh penderia ladang solar. Dua set data untuk setiap loji tenaga suria telah disusun menjadi df panda.
Data daripada Loji Tenaga Suria 1 (SP1) dan Loji Tenaga Suria 2 (SP2) dikumpul setiap 15 minit dari 15 Mei 2020 hingga 18 Jun 2020. Kedua-dua set data SP1 dan SP2 mengandungi pembolehubah yang sama.
- Masa Tarikh - selang 15 minit
- Suhu ambien - suhu udara di sekeliling modul
- Suhu modul - suhu modul
- Penyinaran—— Sinaran pada modul
- Kuasa DC (kW) -DC
- Kuasa AC (kW) -AC
- Hasil Harian-Jumlah penjanaan kuasa harian
- Jumlah Hasil - Hasil kumulatif penyongsang
- ID Loji - Pengenalpastian unik loji kuasa solar
- ID Modul - Pengenalpastian unik setiap modul
Untuk penderia cuaca Untuk merekodkan suhu ambien, suhu modul dan sinaran setiap loji tenaga solar.
Untuk set data ini kuasa DC akan menjadi pembolehubah bersandar (pembolehubah sasaran). Matlamat kami adalah untuk cuba mencari modul solar berprestasi rendah.
Dua df bebas untuk analisis dan ramalan. Satu-satunya perbezaan ialah data yang digunakan untuk peramalan disampel semula kepada selang setiap jam, manakala bingkai data yang digunakan untuk analisis mengandungi selang 15 minit.
Mula-mula kami mengalih keluar Plant ID kerana ia tidak menambah nilai untuk cuba menjawab soalan di atas. ID modul juga dialih keluar daripada set data ramalan. Jadual 1 dan 2 menunjukkan contoh data.


Sebelum meneruskan menganalisis data, kami membuat beberapa andaian tentang loji tenaga solar, termasuk:
- Instrumen pemerolehan data adalah sempurna
- Modul dibersihkan dengan kerap (mengabaikan kesan penyelenggaraan)
- Tiada masalah oklusi di sekitar dua loji tenaga solar
Analisis data penerokaan ( EDA)
Bagi mereka yang baru dalam sains data, EDA ialah langkah penting dalam memahami data dengan memplot visualisasi dan melaksanakan ujian statistik. Mula-mula kita boleh memerhati prestasi setiap loji tenaga solar dengan memplot DC dan AC untuk SP1 dan SP2.
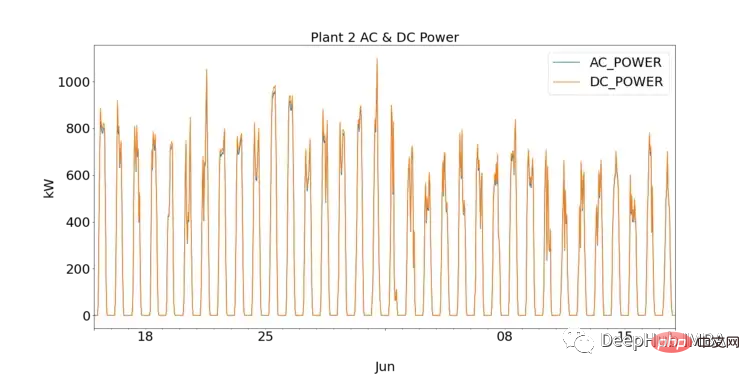
SP1 menunjukkan susunan magnitud kuasa DC yang lebih tinggi daripada sp2. Dengan mengandaikan bahawa data yang dikumpul oleh SP1 adalah betul dan instrumen yang digunakan untuk merekod data tidak rosak, ini bermakna penyongsang dalam SP1 perlu dikaji dengan lebih mendalam
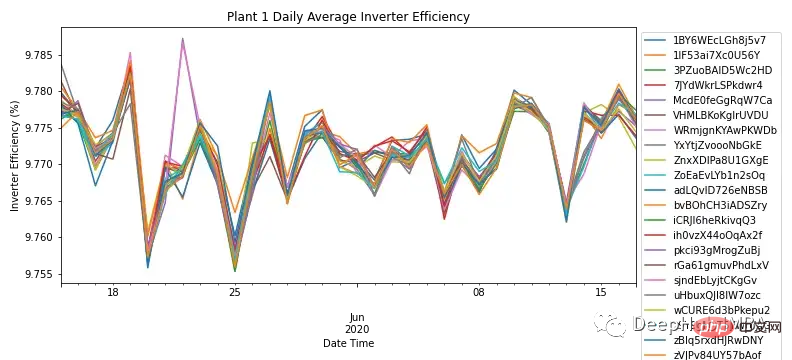
Dengan menekan setiap Kuasa AC dan DC agregat frekuensi harian setiap modul, Rajah 3 menunjukkan kecekapan penyongsang bagi semua modul dalam SP1. Mengikut pengetahuan di lapangan, kecekapan penyongsang suria hendaklah antara 93-96%. Oleh kerana julat kecekapan untuk semua modul ialah 9.76% - 9.79%, ini menggambarkan keperluan untuk menyiasat prestasi penyongsang dan sama ada ia perlu diganti.
Memandangkan SP1 menunjukkan masalah dengan penyongsang, analisis lanjut hanya dilakukan pada SP2.
Walaupun analisis kecil ini adalah hasil daripada lebih banyak masa yang dihabiskan pada penyongsang, ia tidak menjawab persoalan utama dalam menentukan prestasi modul solar.
Memandangkan penyongsang SP2 berfungsi dengan baik, sebarang anomali boleh dikenal pasti dan disiasat dengan mendalami data.
Rajah 4 menunjukkan hubungan antara suhu modul dan suhu ambien, dan terdapat kes di mana suhu modul sangat tinggi.
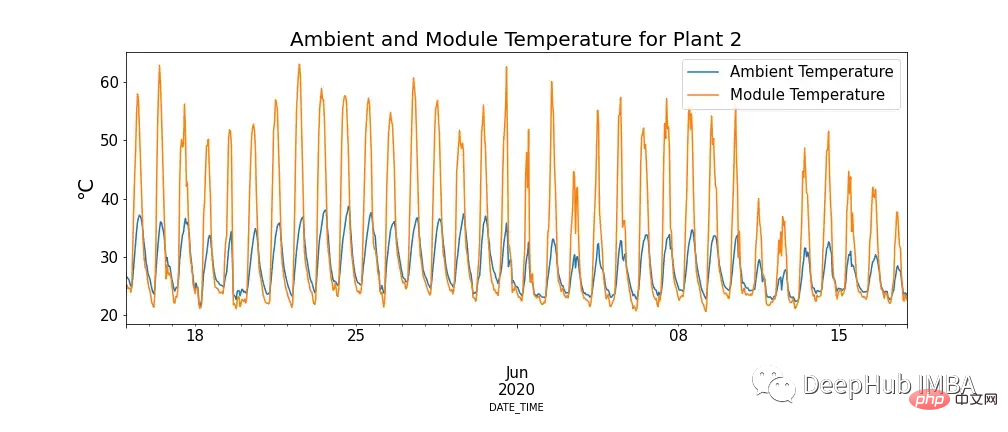
Ini mungkin kelihatan bertentangan dengan pengetahuan kita, tetapi dapat dilihat bahawa suhu tinggi mempunyai kesan negatif pada panel solar. Apabila foton bersentuhan dengan elektron dalam sel suria, ia membebaskan elektron bebas, tetapi pada suhu yang lebih tinggi, lebih banyak elektron sudah berada dalam keadaan teruja, yang mengurangkan voltan yang boleh dihasilkan oleh panel, dengan itu mengurangkan kecekapan.
Mengambil kira fenomena ini, Rajah 5 di bawah menunjukkan suhu modul dan kuasa DC untuk SP2 (titik data di mana suhu ambien lebih rendah daripada suhu modul dan masa dalam hari apabila modul berjalan dengan nombor yang lebih rendah telah ditapis, untuk mengelakkan data condong).
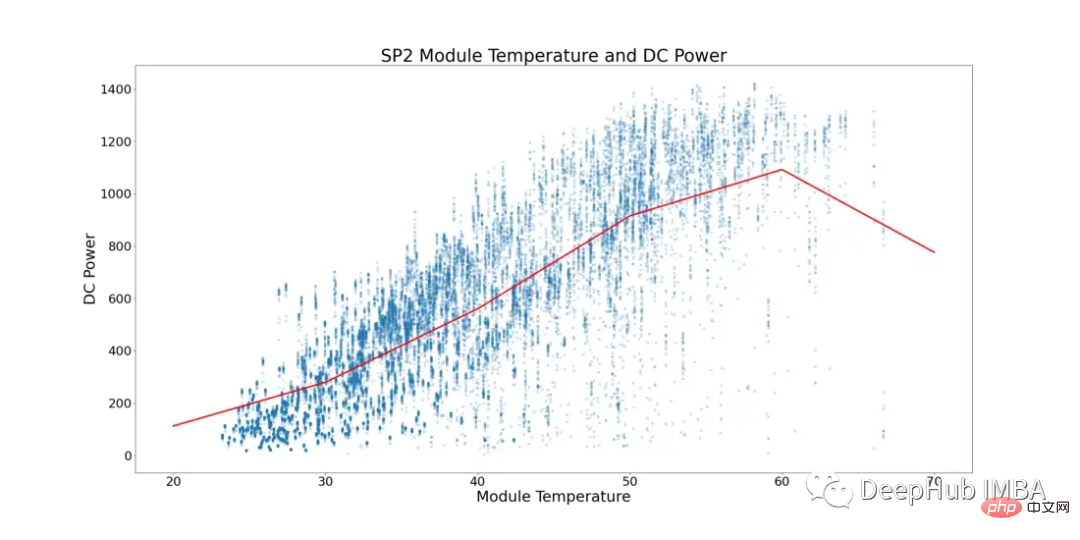
Dalam Rajah 5, garis merah mewakili suhu purata. Anda boleh lihat di sini bahawa terdapat titik tip yang jelas dan tanda-tanda genangan kuasa DC. Mula mendatar pada ~52°C. Untuk mencari modul solar dengan prestasi suboptimum, semua baris yang menunjukkan suhu modul melebihi 52°C telah dialih keluar.
Rajah 6 di bawah menunjukkan kuasa DC setiap modul dalam SP2 dalam tempoh sehari. Ini pada asasnya memenuhi jangkaan, dan penjanaan kuasa lebih besar pada waktu tengah hari. Tetapi terdapat satu lagi masalah semasa tempoh operasi puncak, penjanaan kuasa adalah rendah. Sukar untuk kami merumuskan sebab-sebab keadaan ini, kerana keadaan cuaca mungkin buruk pada hari itu, atau SP2 mungkin memerlukan penyelenggaraan rutin, dll.
Terdapat juga tanda-tanda modul berprestasi rendah dalam Rajah 6. Ia boleh dikenal pasti sebagai modul (titik data individu) pada graf yang menyimpang daripada kelompok terdekat.

Untuk menentukan modul yang berprestasi lemah, kami boleh melakukan ujian statistik sambil membandingkan prestasi setiap modul dengan modul lain untuk menentukan prestasi.
Setiap 15 minit, pengagihan bekalan kuasa DC modul yang berbeza pada masa yang sama adalah pengedaran normal Melalui ujian hipotesis, ia boleh ditentukan modul mana yang berprestasi lemah. Kiraan ialah bilangan kali modul berada di luar selang keyakinan 99.9% dengan nilai p
Rajah 7 menunjukkan dalam tertib menurun bilangan kali setiap modul secara statistik lebih rendah daripada modul lain dalam tempoh yang sama.

Daripada Rajah 7 adalah jelas bahawa modul 'Quc1TzYxW2pYoWX' bermasalah. Maklumat ini boleh diberikan kepada kakitangan SP2 yang berkaitan untuk menyiasat puncanya.
Pemodelan
Di bawah ini kita mula menggunakan tiga algoritma siri masa yang berbeza: SARIMA, XGBoost dan CNN-LSTM, untuk memodelkan dan membandingkan
untuk ketiga-tiga model , kedua-duanya menggunakan ramalan titik data seterusnya untuk ramalan. Pengesahan berjalan ke hadapan ialah teknik yang digunakan dalam pemodelan siri masa kerana ramalan menjadi kurang tepat dari semasa ke semasa, jadi pendekatan yang lebih praktikal ialah melatih semula model dengan data sebenar apabila ia tersedia.
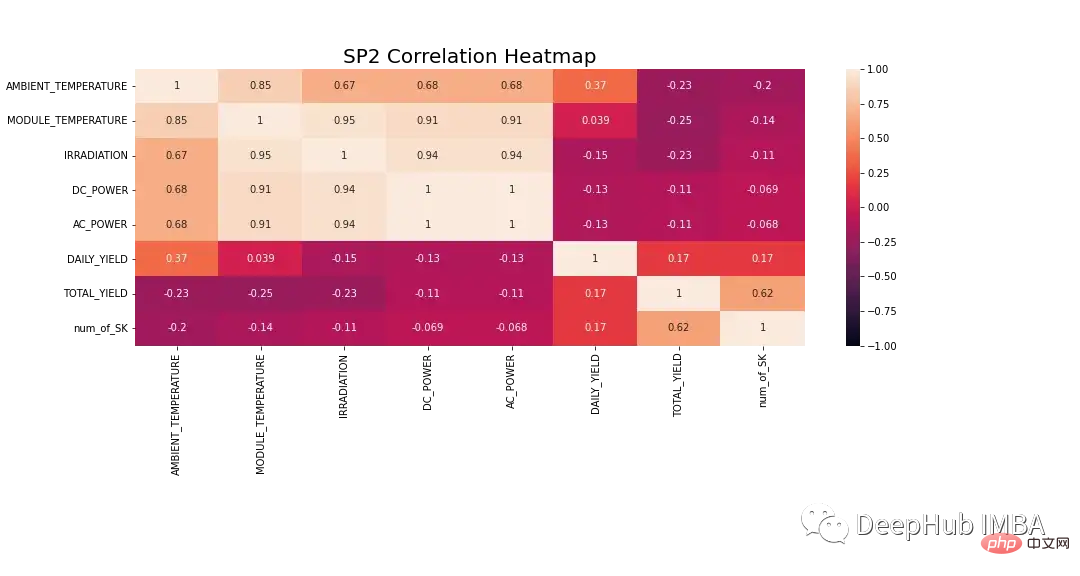
Data perlu dikaji dengan lebih terperinci sebelum dimodelkan. Rajah 8 menunjukkan peta haba korelasi untuk semua ciri dalam set data SP2. Peta haba menunjukkan korelasi kuat pembolehubah bersandar, kuasa DC, dengan suhu modul, penyinaran dan suhu ambien. Ciri-ciri ini mungkin memainkan peranan penting dalam ramalan.
Dalam peta haba di bawah, kuasa AC menunjukkan pekali korelasi Pearson 1. Untuk mengelakkan isu kebocoran data, kami mengalih keluar kuasa DC daripada data.
SARIMA
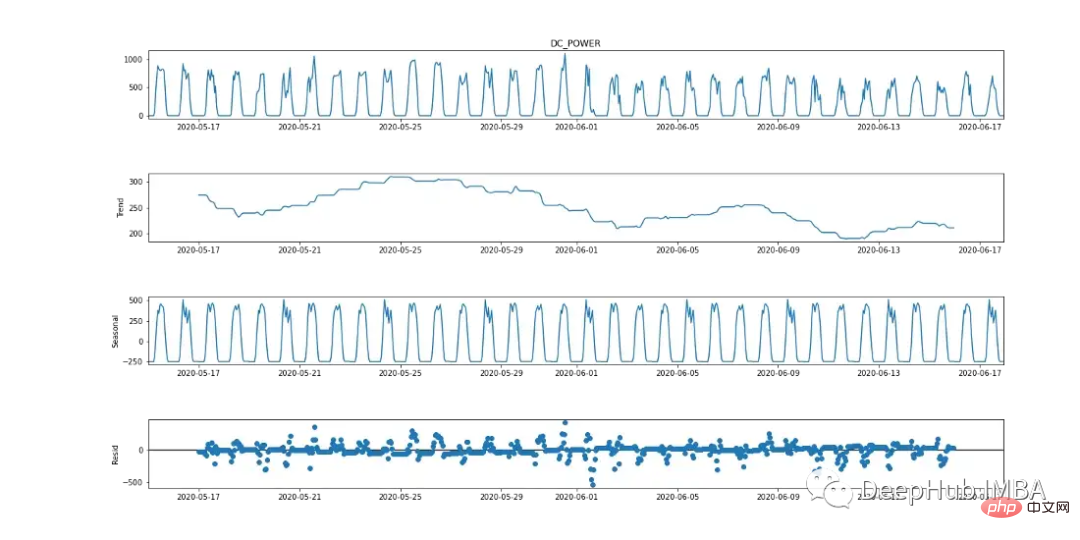
Purata Pergerakan Bersepadu Autoregresif Bermusim (SARIMA) ialah kaedah ramalan siri masa univariate. Memandangkan pembolehubah sasaran menunjukkan tanda-tanda tempoh kitaran 24 jam, SARIMA ialah pilihan pemodelan yang cekap kerana ia mengambil kira kesan bermusim. Ini boleh diperhatikan dalam carta pecahan bermusim di bawah.
Algoritma SARIMA memerlukan data pegun. Terdapat pelbagai cara untuk menguji sama ada data adalah pegun, seperti ujian statistik (ujian Dickey-Fowler tambahan), statistik ringkasan (membandingkan min/varian bahagian data yang berbeza) dan menganalisis data secara visual. Adalah penting untuk menjalankan beberapa ujian sebelum pemodelan.
Ujian Augmented Dickey-Fuller (ADF) ialah "ujian akar unit" yang digunakan untuk menentukan sama ada siri masa adalah pegun. Pada asasnya, ia adalah ujian keertian statistik di mana terdapat hipotesis nol dan hipotesis alternatif dan kesimpulan dibuat berdasarkan nilai-p yang terhasil.
Hipotesis nol: Data siri masa adalah tidak pegun.
Hipotesis alternatif: Data siri masa adalah pegun.
Dalam contoh kami, jika nilai p ≤ 0.05, kami boleh menolak hipotesis nol dan mengesahkan bahawa data tidak mempunyai punca unit.
from statsmodels.tsa.stattools import adfuller
result = adfuller(plant2_dcpower.values)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('t%s: %.3f' % (key, value))
Daripada ujian ADF, nilai p ialah 0.000553, < 0.05. Berdasarkan statistik ini, data boleh dianggap stabil. Walau bagaimanapun, melihat Rajah 2 (graf atas), terdapat tanda-tanda bermusim yang jelas (untuk data siri masa dianggap pegun, tidak sepatutnya ada tanda-tanda kemusim dan arah aliran), menunjukkan bahawa data itu tidak pegun. Oleh itu, adalah penting untuk menjalankan pelbagai ujian. < 0.05。根据这一统计数据,可以认为该数据是稳定的。然而,查看图2(最上面的图),有明显的季节性迹象(对于被认为是平稳的时间序列数据,不应该有季节性和趋势的迹象),这说明数据是非平稳的。因此,运行多个测试非常重要。
Untuk memodelkan pembolehubah bersandar dengan SARIMA, siri masa perlu pegun. Seperti yang ditunjukkan dalam Rajah 9 (graf pertama dan ketiga), kuasa DC mempunyai tanda bermusim yang jelas. Ambil perbezaan pertama [t-(t-1)] untuk mengeluarkan komponen bermusim, seperti yang ditunjukkan dalam Rajah 10, kerana ia kelihatan serupa dengan taburan normal. Data kini tidak bergerak dan sesuai untuk algoritma SARIMA.
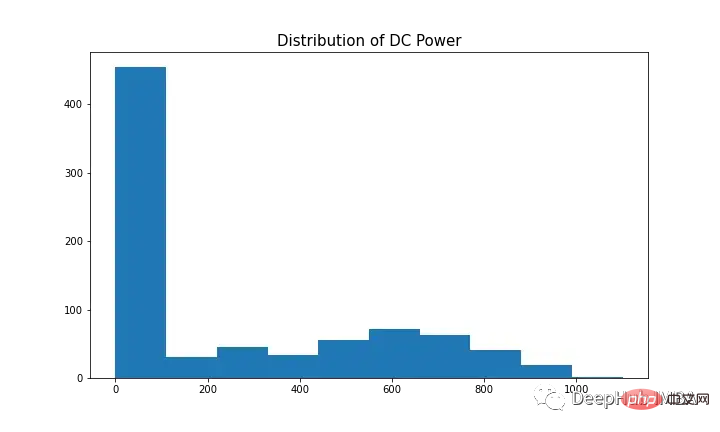
Hiperparameter SARIMA termasuk p (urutan autoregresif), d (urutan perbezaan), q (urutan purata bergerak), p (urutan autoregresif bermusim) ), d (urutan perbezaan bermusim ), q (perintah purata bergerak bermusim), m (langkah masa kitaran bermusim), arah aliran (trend deterministik).
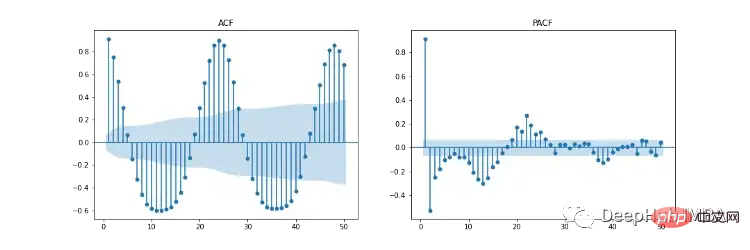
Rajah 11 menunjukkan autokorelasi (ACF), autokorelasi separa (PACF) dan plot ACF/PACF bermusim. Plot ACF menunjukkan korelasi antara siri masa dan versi tertundanya. PACF menunjukkan korelasi langsung antara siri masa dan versi ketinggalannya. Kawasan berlorek biru mewakili selang keyakinan. SACF dan SPACF boleh dikira dengan mengambil perbezaan bermusim (m) daripada data asal, dalam kes ini 24 kerana terdapat kesan bermusim 24 jam yang jelas dalam plot ACF.
Menurut gerak hati kami, titik permulaan hiperparameter boleh diperoleh daripada plot ACF dan PACF. Sebagai contoh, kedua-dua ACF dan PACF menunjukkan arah aliran menurun secara beransur-ansur, iaitu tertib autoregresif (p) dan tertib purata bergerak (q) kedua-duanya lebih besar daripada 0. p dan p boleh ditentukan dengan melihat plot PCF dan SPCF masing-masing, dan mengira bilangan ketinggalan yang menjadi signifikan secara statistik sebelum nilai ketinggalan menjadi tidak ketara. Begitu juga, q dan q boleh didapati dalam rajah ACF dan SACF.
Tertib perbezaan (d) boleh ditentukan dengan bilangan perbezaan yang menjadikan data pegun. Susunan perbezaan musim (D) dianggarkan daripada bilangan perbezaan yang diperlukan untuk mengalih keluar komponen bermusim daripada siri masa.
Anda boleh membaca artikel ini untuk pilihan hiperparameter ini: https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html
Anda juga boleh menggunakan kaedah carian grid untuk pengoptimuman hiperparameter , pilih hiperparameter optimum berdasarkan ralat min kuasa dua (MSE) minimum, termasuk p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, trend = ' n ' (tiada trend).
from time import time
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
print(f'SARIMA runtime: {round(time_len/60,2)} mins')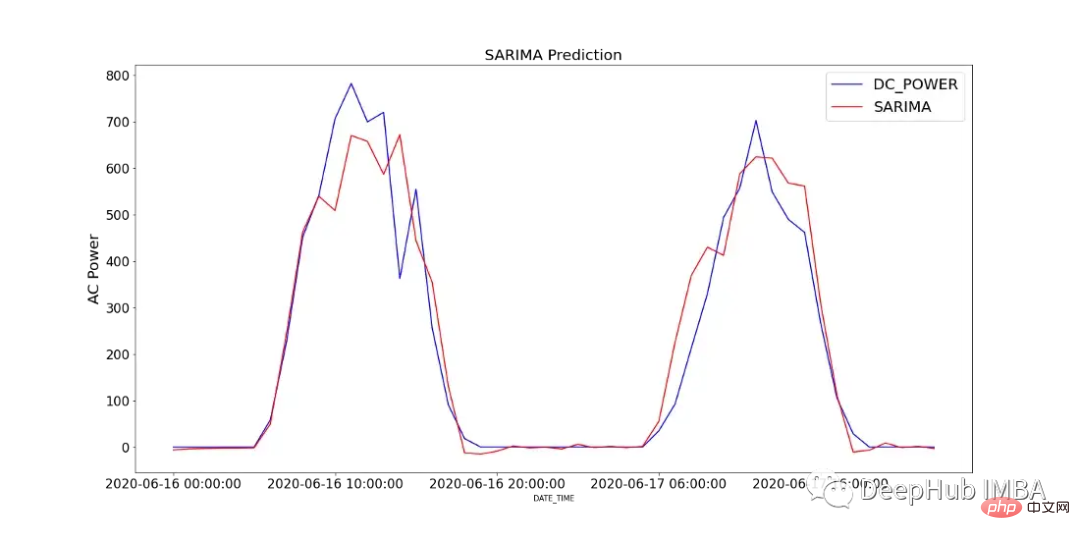
Rajah 12 menunjukkan perbandingan nilai ramalan model SARIMA dengan kuasa DC yang direkodkan dalam SP2 selama 2 hari.
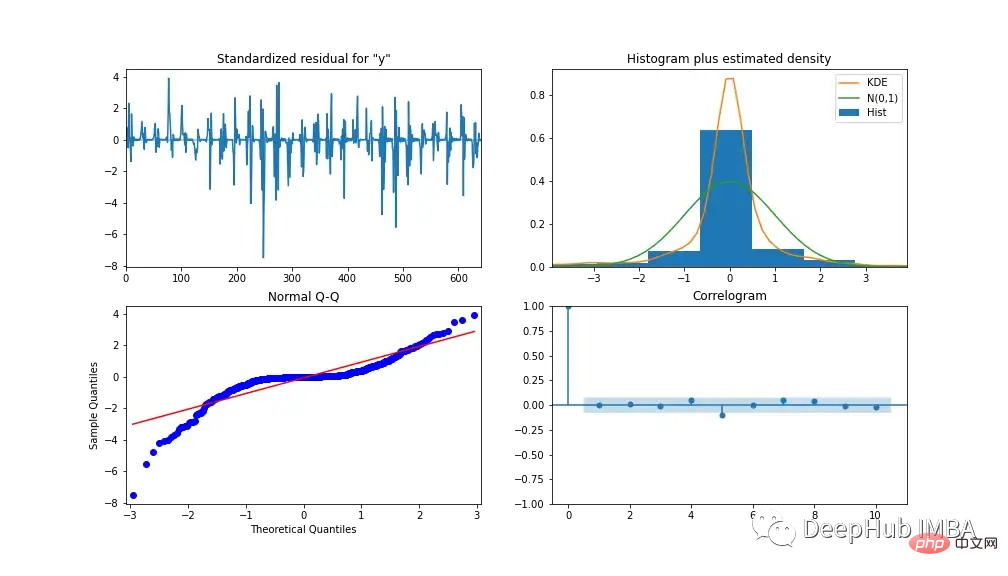
Untuk menganalisis prestasi model, Rajah 13 menunjukkan diagnostik model. Plot korelasi menunjukkan hampir tiada korelasi selepas ketinggalan pertama, dan histogram di bawah menunjukkan taburan normal di sekitar min sifar. Daripada ini kita boleh mengatakan bahawa model tidak boleh mengumpul maklumat lanjut daripada data.
XGBoost
XGBoost (EXtreme Gradient Boosting) ialah algoritma pepohon keputusan meningkatkan kecerunan. Ia menggunakan pendekatan ensemble di mana model pepohon keputusan baharu ditambah untuk mengubah suai skor pepohon keputusan sedia ada. Tidak seperti SARIMA, XGBoost ialah algoritma pembelajaran mesin berbilang variasi, yang bermaksud model itu boleh menggunakan berbilang ciri untuk meningkatkan prestasi model.
Kami menggunakan kejuruteraan ciri untuk meningkatkan ketepatan model. 3 ciri tambahan turut dicipta, termasuk versi ketinggalan kuasa AC dan DC, masing-masing S1_AC_POWER dan S1_DC_POWER, dan kecekapan keseluruhan EFF, iaitu kuasa AC dibahagikan dengan kuasa DC. Dan alih keluar AC_POWER dan MODULE_TEMPERATURE daripada data. Rajah 14 menunjukkan tahap kepentingan ciri mengikut keuntungan (keuntungan purata pemisahan menggunakan ciri) dan berat (bilangan kali ciri muncul dalam pokok).

Tentukan hiperparameter yang digunakan dalam pemodelan melalui carian grid Hasilnya ialah: *kadar pembelajaran = 0.01, bilangan penganggar = 1200, subsampel = 0.8, colsample mengikut pokok = 1. , sampel sampel mengikut tahap = 1, berat kanak-kanak min = 20 dan kedalaman maksimum = 10
Kami menggunakan MinMaxScaler untuk menskalakan data latihan kepada antara 0 dan 1 (anda juga boleh bereksperimen dengan penimbang lain seperti log-transform dan penskala piawai, yang bergantung pada pengedaran data). Tukar data kepada set data pembelajaran yang diselia dengan mengalihkan semua pembolehubah bebas ke belakang mengikut jumlah masa tertentu.
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.preprocessing import MinMaxScaler
from time import time
def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
return result, test, xgb_model
if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
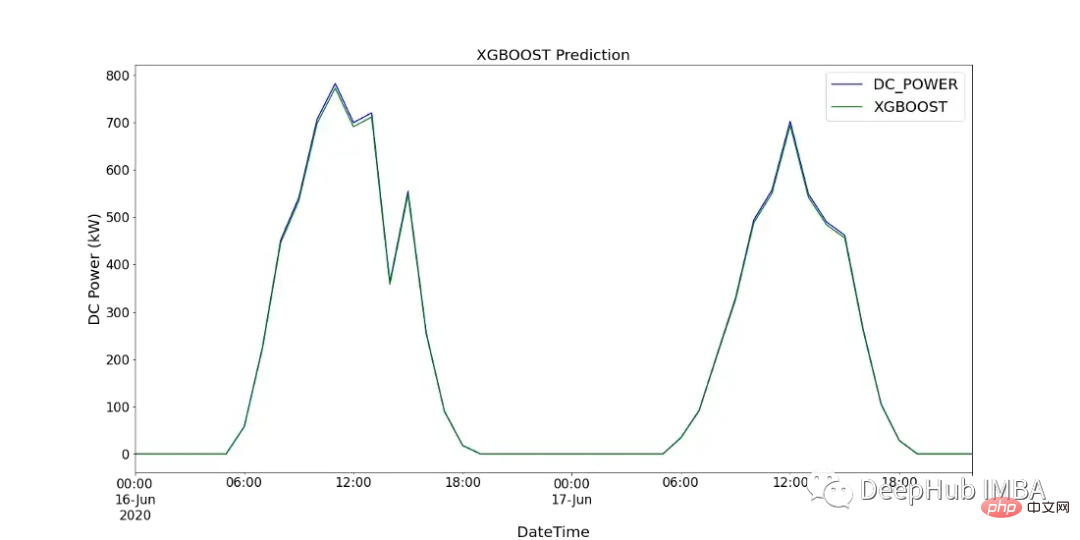
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。
CNN-LSTM
CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络,在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型,旨在解决长期存在的梯度爆炸/消失问题,使用内部存储系统,允许它在输入序列上积累状态。
在本例中,使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入,所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似,使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放,但范围在-1到1之间。对于CNN-LSTM,需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features],以便可以将其作为输入传递给模型。
由于我们希望为每个子序列重用相同的CNN模型,因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。
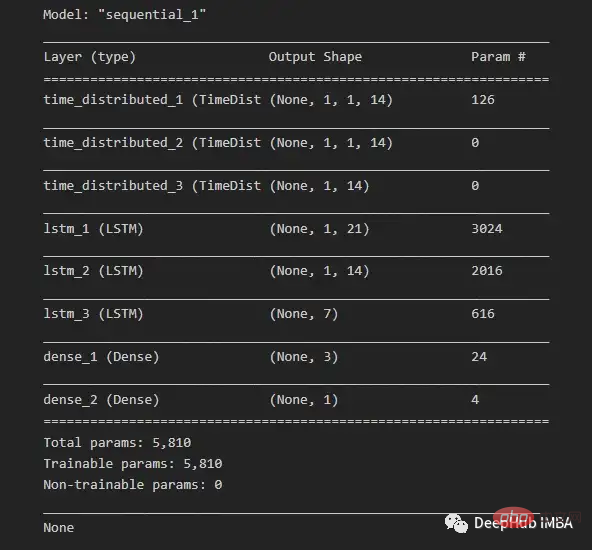
在将数据分解为训练数据和测试数据之后,将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后,模型可以进一步使用这一点来评估模型的性能。
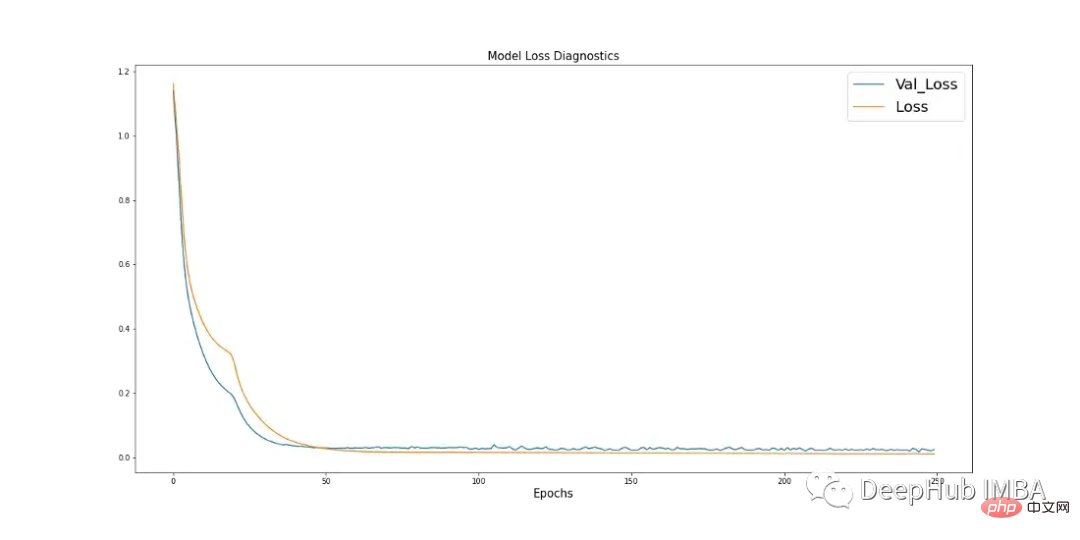
学习曲线是深度学习中使用的一个很好的诊断工具,它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习,并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
import keras
from keras.models import Sequential
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
from keras.optimizers import Adam
n_steps = 1
subseq = 1
def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
return np.array(x), np.array(y)
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
return model, history
# split and resahpe data
train, test = train_test_split(dropped_df_cat)
train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
#scale data
scaler_x = MinMaxScaler(feature_range=(-1,1))
scaler_y = MinMaxScaler(feature_range=(-1,1))
train_x = scaler_x.fit_transform(train_x)
train_y = scaler_y.fit_transform(train_y)
test_x = scaler_x.transform(test_x)
test_y = scaler_y.transform(test_y)
# shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
train_data_np = np.hstack((train_x, train_y))
x, y = split_data(train_data_np, n_steps)
x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
# create validation set
x_val, y_val = x_subseq[-24:], y[-24:]
x_train, y_train = x_subseq[:-24], y[:-24]
n_features = x.shape[2]
actual = scaler_y.inverse_transform(test_y)
# run CNN-LSTM model
if __name__ == '__main__':
start_time = time()
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
print(f"CNN-LSTM MSE: {round(mse,2)}")图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。
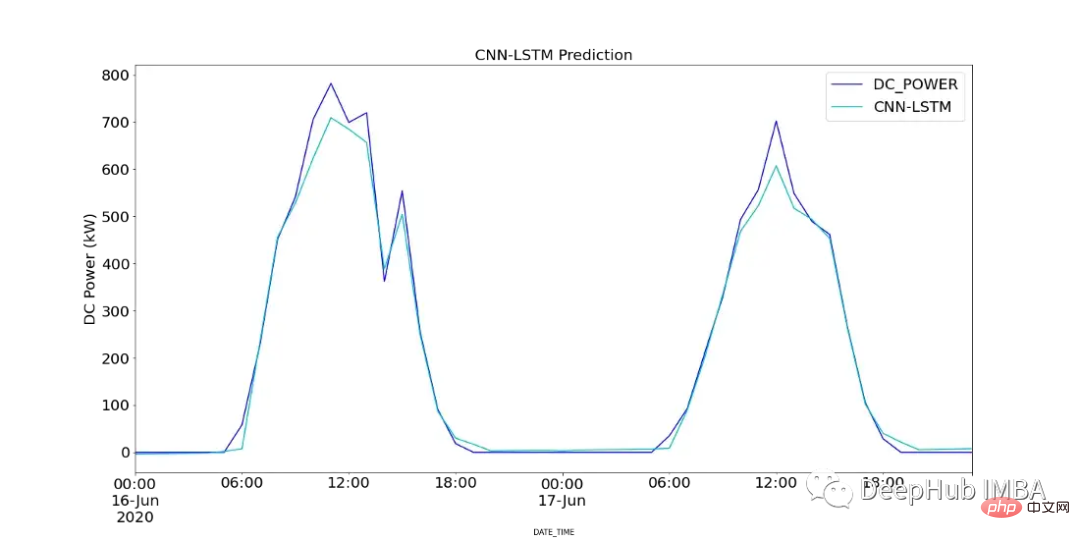
由于CNN-LSTM的随机性,该模型运行10次,并记录一个平均MSE值作为最终值,以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。
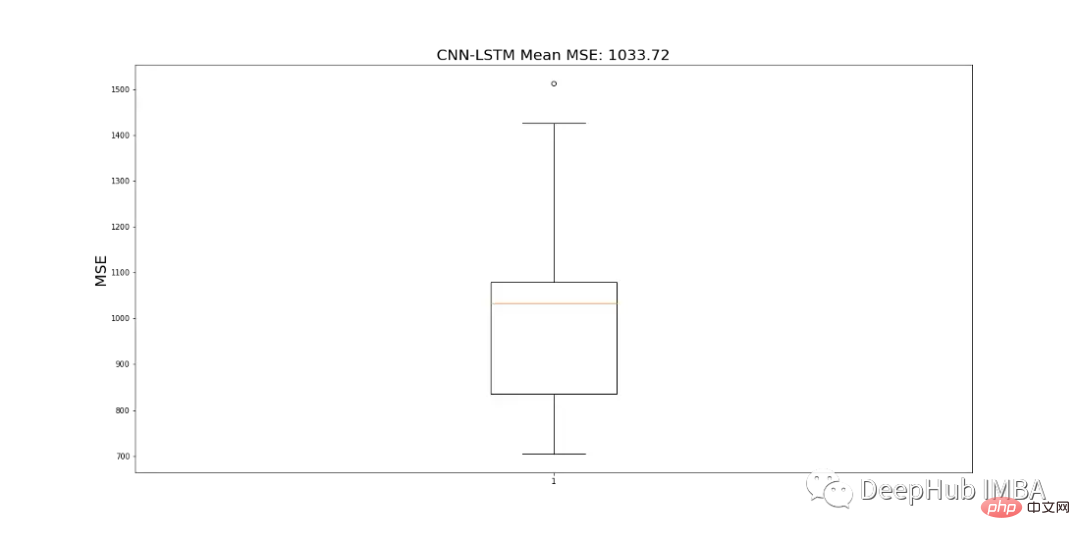
结果对比
下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。
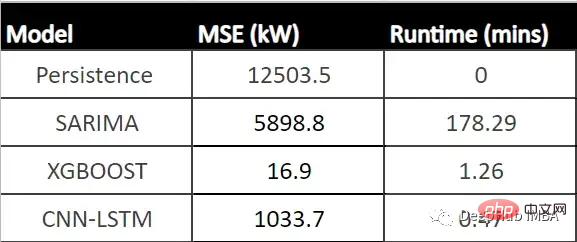
从表中可以看出,XGBoost的MSE最低、运行时第二快,并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时,它可以成为帮助运营经理决策过程的强大工具。
总结
在本文中我们分析了SP1和SP2,确定SP1性能较低。所以对SP2的进一步调查显示,并且查看了SP2中那些模块性能可能有问题,并使用假设检验来计算每个模块在统计上明显表现不佳的次数,' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。
我们使用数据训练三个模型:SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差,XGBOOST表现最好,MSE为16.9,运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。
Atas ialah kandungan terperinci Bandingkan kaedah ramalan siri masa berdasarkan SARIMA, XGBoost dan CNN-LSTM.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1662
1662
 14
14
 1419
1419
 52
52
 1313
1313
 25
25
 1262
1262
 29
29
 1235
1235
 24
24
 15 alat anotasi imej percuma sumber terbuka disyorkan
Mar 28, 2024 pm 01:21 PM
15 alat anotasi imej percuma sumber terbuka disyorkan
Mar 28, 2024 pm 01:21 PM
Anotasi imej ialah proses mengaitkan label atau maklumat deskriptif dengan imej untuk memberi makna dan penjelasan yang lebih mendalam kepada kandungan imej. Proses ini penting untuk pembelajaran mesin, yang membantu melatih model penglihatan untuk mengenal pasti elemen individu dalam imej dengan lebih tepat. Dengan menambahkan anotasi pada imej, komputer boleh memahami semantik dan konteks di sebalik imej, dengan itu meningkatkan keupayaan untuk memahami dan menganalisis kandungan imej. Anotasi imej mempunyai pelbagai aplikasi, meliputi banyak bidang, seperti penglihatan komputer, pemprosesan bahasa semula jadi dan model penglihatan graf Ia mempunyai pelbagai aplikasi, seperti membantu kenderaan dalam mengenal pasti halangan di jalan raya, dan membantu dalam proses. pengesanan dan diagnosis penyakit melalui pengecaman imej perubatan. Artikel ini terutamanya mengesyorkan beberapa alat anotasi imej sumber terbuka dan percuma yang lebih baik. 1.Makesen
 Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Artikel ini akan membawa anda memahami SHAP: penjelasan model untuk pembelajaran mesin
Jun 01, 2024 am 10:58 AM
Dalam bidang pembelajaran mesin dan sains data, kebolehtafsiran model sentiasa menjadi tumpuan penyelidik dan pengamal. Dengan aplikasi meluas model yang kompleks seperti kaedah pembelajaran mendalam dan ensemble, memahami proses membuat keputusan model menjadi sangat penting. AI|XAI yang boleh dijelaskan membantu membina kepercayaan dan keyakinan dalam model pembelajaran mesin dengan meningkatkan ketelusan model. Meningkatkan ketelusan model boleh dicapai melalui kaedah seperti penggunaan meluas pelbagai model yang kompleks, serta proses membuat keputusan yang digunakan untuk menerangkan model. Kaedah ini termasuk analisis kepentingan ciri, anggaran selang ramalan model, algoritma kebolehtafsiran tempatan, dsb. Analisis kepentingan ciri boleh menerangkan proses membuat keputusan model dengan menilai tahap pengaruh model ke atas ciri input. Anggaran selang ramalan model
 Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Kenal pasti overfitting dan underfitting melalui lengkung pembelajaran
Apr 29, 2024 pm 06:50 PM
Artikel ini akan memperkenalkan cara mengenal pasti pemasangan lampau dan kekurangan dalam model pembelajaran mesin secara berkesan melalui keluk pembelajaran. Underfitting dan overfitting 1. Overfitting Jika model terlampau latihan pada data sehingga ia mempelajari bunyi daripadanya, maka model tersebut dikatakan overfitting. Model yang dipasang terlebih dahulu mempelajari setiap contoh dengan sempurna sehingga ia akan salah mengklasifikasikan contoh yang tidak kelihatan/baharu. Untuk model terlampau, kami akan mendapat skor set latihan yang sempurna/hampir sempurna dan set pengesahan/skor ujian yang teruk. Diubah suai sedikit: "Punca overfitting: Gunakan model yang kompleks untuk menyelesaikan masalah mudah dan mengekstrak bunyi daripada data. Kerana set data kecil sebagai set latihan mungkin tidak mewakili perwakilan yang betul bagi semua data. 2. Underfitting Heru
 Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Evolusi kecerdasan buatan dalam penerokaan angkasa lepas dan kejuruteraan penempatan manusia
Apr 29, 2024 pm 03:25 PM
Pada tahun 1950-an, kecerdasan buatan (AI) dilahirkan. Ketika itulah penyelidik mendapati bahawa mesin boleh melakukan tugas seperti manusia, seperti berfikir. Kemudian, pada tahun 1960-an, Jabatan Pertahanan A.S. membiayai kecerdasan buatan dan menubuhkan makmal untuk pembangunan selanjutnya. Penyelidik sedang mencari aplikasi untuk kecerdasan buatan dalam banyak bidang, seperti penerokaan angkasa lepas dan kelangsungan hidup dalam persekitaran yang melampau. Penerokaan angkasa lepas ialah kajian tentang alam semesta, yang meliputi seluruh alam semesta di luar bumi. Angkasa lepas diklasifikasikan sebagai persekitaran yang melampau kerana keadaannya berbeza daripada di Bumi. Untuk terus hidup di angkasa, banyak faktor mesti dipertimbangkan dan langkah berjaga-jaga mesti diambil. Para saintis dan penyelidik percaya bahawa meneroka ruang dan memahami keadaan semasa segala-galanya boleh membantu memahami cara alam semesta berfungsi dan bersedia untuk menghadapi kemungkinan krisis alam sekitar
 Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Telus! Analisis mendalam tentang prinsip model pembelajaran mesin utama!
Apr 12, 2024 pm 05:55 PM
Dalam istilah orang awam, model pembelajaran mesin ialah fungsi matematik yang memetakan data input kepada output yang diramalkan. Secara lebih khusus, model pembelajaran mesin ialah fungsi matematik yang melaraskan parameter model dengan belajar daripada data latihan untuk meminimumkan ralat antara output yang diramalkan dan label sebenar. Terdapat banyak model dalam pembelajaran mesin, seperti model regresi logistik, model pepohon keputusan, model mesin vektor sokongan, dll. Setiap model mempunyai jenis data dan jenis masalah yang berkenaan. Pada masa yang sama, terdapat banyak persamaan antara model yang berbeza, atau terdapat laluan tersembunyi untuk evolusi model. Mengambil perceptron penyambung sebagai contoh, dengan meningkatkan bilangan lapisan tersembunyi perceptron, kita boleh mengubahnya menjadi rangkaian neural yang mendalam. Jika fungsi kernel ditambah pada perceptron, ia boleh ditukar menjadi SVM. yang ini
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada
 Adakah Flash Attention stabil? Meta dan Harvard mendapati bahawa sisihan berat model mereka berubah-ubah mengikut urutan magnitud
May 30, 2024 pm 01:24 PM
Adakah Flash Attention stabil? Meta dan Harvard mendapati bahawa sisihan berat model mereka berubah-ubah mengikut urutan magnitud
May 30, 2024 pm 01:24 PM
MetaFAIR bekerjasama dengan Harvard untuk menyediakan rangka kerja penyelidikan baharu untuk mengoptimumkan bias data yang dijana apabila pembelajaran mesin berskala besar dilakukan. Adalah diketahui bahawa latihan model bahasa besar sering mengambil masa berbulan-bulan dan menggunakan ratusan atau bahkan ribuan GPU. Mengambil model LLaMA270B sebagai contoh, latihannya memerlukan sejumlah 1,720,320 jam GPU. Melatih model besar memberikan cabaran sistemik yang unik disebabkan oleh skala dan kerumitan beban kerja ini. Baru-baru ini, banyak institusi telah melaporkan ketidakstabilan dalam proses latihan apabila melatih model AI generatif SOTA Mereka biasanya muncul dalam bentuk lonjakan kerugian Contohnya, model PaLM Google mengalami sehingga 20 lonjakan kerugian semasa proses latihan. Bias berangka adalah punca ketidaktepatan latihan ini,



