Bagaimana untuk melaksanakan pokok ketinggian minimum di Jawa

Keperluan masalah

Pokok ialah graf tidak terarah di mana mana-mana dua bucu disambungkan dengan hanya satu laluan. Dalam erti kata lain, mana-mana graf bersambung tanpa kitaran mudah ialah pokok.

Anda diberi pokok yang mengandungi n nod, dilabelkan 0 hingga n - 1 . Diberi nombor n dan senarai tepi dengan n - 1 tepi tidak terarah (setiap tepi ialah sepasang label), di mana tepi[i] = [ai, bi] bermakna terdapat tepi antara nod ai dan bi dalam pokok Tidak terarah tepi.

Anda boleh memilih mana-mana nod dalam pokok sebagai akar. Apabila nod x dipilih sebagai nod akar, biarkan ketinggian pokok hasil ialah h. Di antara semua pokok yang mungkin, pokok dengan ketinggian minimum (iaitu, min(h)) dipanggil pokok ketinggian minimum .

Sila cari semua pokok ketinggian minimum dan kembalikan senarai label nod akarnya dalam sebarang susunan.

Ketinggian pokok merujuk kepada bilangan tepi pada laluan ke bawah terpanjang antara nod akar dan nod daun.

Contoh 1:

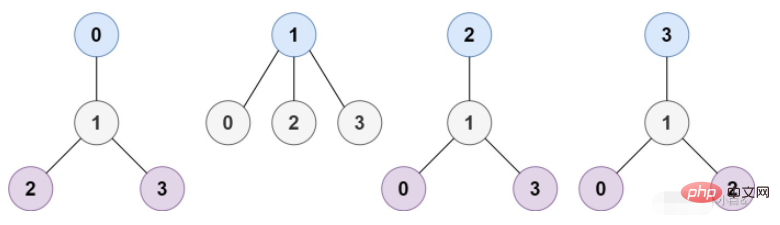
Input: n = 4, tepi = [[1,0],[1,2],[1,3] ]
Output: [1]
Penjelasan: Seperti yang ditunjukkan dalam rajah, apabila punca ialah nod dengan label 1, ketinggian pokok ialah 1, iaitu satu-satunya pokok ketinggian minimum.

Contoh 2:

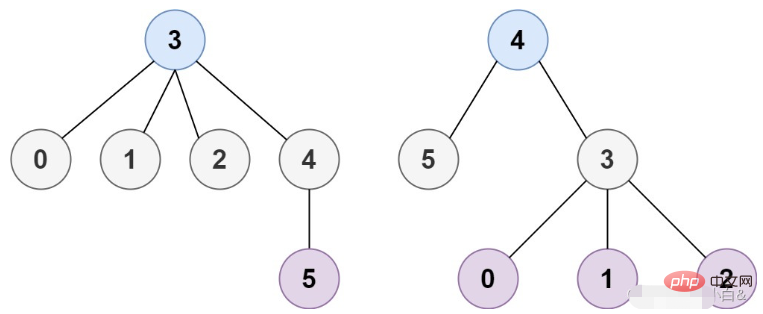
Input: n = 6, tepi = [[3,0],[3,1],[3 ,2],[3,4],[5,4]]
Output: [3,4]

Prompt:
1 tepi.panjang == n - 1
0 ai != bi
Semua (ai, bi) berbeza antara satu sama lain
Input yang diberikan dijamin sebagai pokok, dan tidak akan ada tepi berulang

Idea penyelesaian masalah

  Daripada dua rajah di atas, kita boleh buat kesimpulan: Apa yang perlu diselesaikan dalam masalah ini ialah nod pusat dalam pokok, dan setiap pokok akan mempunyai tidak lebih daripada dua nod pusat.

  Dan jika kita ingin mendapatkan nod pusat dalam pokok, kita boleh FBS lapisan demi lapisan (iaitu, memotong nod daun dengan keluar-darjah satu lapisan demi lapisan) sehingga lapisan terakhir dipotong, anda boleh mengeluarkan hasilnya!

Algoritma

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> res = new ArrayList<Integer>();
        //如果只有一个节点，则它就是最小高度树
        if(n == 1){
            res.add(0);
            return res;
        }

        //每个节点的邻居数量
        int [] degree = new int[n];
        //每个节点的邻居
        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int [] edge : edges){
            int a = edge[0];
            int b = edge[1];

            degree[a]++;
            degree[b]++;

            if(map.get(a) == null){
                map.put(a,new ArrayList<Integer>());//key:节点   value:邻居
            }

            if(map.get(b) == null){
                map.put(b,new ArrayList<Integer>());//key:节点   value:邻居
            }

            map.get(a).add(b);
            map.get(b).add(a);
        }

        //建立队列
        LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
        //将所有度为1的节点入队
        for(int i = 0;i < degree.length;i++){
            if(degree[i] == 1){
                leafNodes.add(i);
            }
        }

        while(leafNodes.size() > 0){
            res.clear();
            //每一层节点的数量
            int size = leafNodes.size();

            for(int i = 0;i < size;i++){
                int leaf = leafNodes.poll();
                //将当前节点加入到结果集
                res.add(leaf);

                List<Integer> neighbors = map.get(leaf);
                //将出度减一，也就是将最外层的叶子节点剪掉
                for(int neighbor : neighbors){
                    degree[neighbor]--;
                    if(degree[neighbor] == 1){
                        //叶子节点入队
                        leafNodes.add(neighbor);
                    }
                }
            }
        }
        return res;
    }
}

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan pokok ketinggian minimum di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!