 Peranti teknologi
Peranti teknologi
 AI
AI
 Dengan menukar masalah matematik kepada kod, penyelidikan Google telah meningkatkan ketepatan pembuktian mesin.
Dengan menukar masalah matematik kepada kod, penyelidikan Google telah meningkatkan ketepatan pembuktian mesin.
Dengan menukar masalah matematik kepada kod, penyelidikan Google telah meningkatkan ketepatan pembuktian mesin.
Komputer telah digunakan untuk mengesahkan pembuktian matematik untuk beberapa lama, tetapi mereka hanya dapat melakukannya jika masalah disediakan menggunakan bahasa pembuktian yang direka khas dan tidak dapat mengendalikan campuran notasi matematik dan teks bertulis yang digunakan oleh ahli matematik .
Jika anda menukar masalah matematik yang ditulis dalam bahasa semula jadi kepada kod formal dan memudahkan komputer untuk menyelesaikannya, ini mungkin membantu membina mesin yang boleh meneroka penemuan baharu dalam matematik.
Proses ini dipanggil pemformalkan, tetapi hanya pembuktian boleh mengambil masa bertahun-tahun, jadi hanya sebahagian kecil pengetahuan matematik diformalkan dan kemudian dibuktikan oleh mesin.
Autoformalisasi merujuk kepada tugas menerjemahkan matematik secara automatik daripada bahasa semula jadi kepada bahasa formal . Implikasi praktikal dan falsafah daripada alat pemformalkan automatik yang berjaya akan menjadi sangat besar, ia boleh mengurangkan kos pemformalan yang berlebihan semasa, dan dalam jangka panjang, ia boleh menghubungkan aspek automatik penaakulan matematik dalam pelbagai bidang penyelidikan.
Dalam kajian baru-baru ini, Yuhuai Wu dari Google dan rakan usaha samanya menggunakan rangkaian saraf daripada OpenAI Codex untuk mengautomasikan kerja pemformalkan . Codex telah dilatih mengenai sejumlah besar teks dan data pengaturcaraan daripada web, dan pengaturcara boleh menggunakannya untuk menjana kod yang boleh dipercayai.

Pautan kertas: https://arxiv.org/pdf/2205.12615.pdf
Memformalkan 12,500 masalah pertandingan matematik sekolah menengah
Satu siri kemajuan terkini dalam model bahasa berskala besar menunjukkan potensi model untuk memahami bahasa formal. Walau bagaimanapun, kejayaan sedia ada terhad kepada bahasa formal (seperti Python) yang wujud korpora besar di web. Sebaliknya, data matematik formal sangat terhad. Salah satu perpustakaan bahasa matematik rasmi terbesar, Arkib Bukti Formal, hanya bersaiz 180mb, iaitu kurang daripada 0.18% daripada data latihan model bahasa besar Codex.
Tambahan pula, tidak seperti kes untuk bahasa pengaturcaraan tujuan umum, di mana docstring bahasa semula jadi tersedia secara meluas, terdapat sedikit penjajaran data antara bahasa semula jadi dan bahasa matematik formal. Oleh itu, masih tidak diketahui sama ada kejayaan model bahasa berskala besar secara langsung boleh menggalakkan pembangunan pemformalkan automatik.
Memandangkan persamaan antara bahasa bukti dan bahasa pengaturcaraan, pasukan memutuskan untuk melihat sama ada Codex boleh merasmikan perpustakaan 12,500 masalah pertandingan matematik sekolah menengah. Ia mampu menukar satu perempat daripada masalah kepada format yang serasi dengan penyelesai bukti formal Isabelle.
Wu menyatakan bahawa banyak transformasi yang tidak berjaya adalah akibat sistem tidak memahami konsep matematik tertentu. "Jika anda menunjukkan model dengan contoh yang menerangkan konsep, maka model itu boleh memahaminya dengan cepat."
Kerja ini meneroka prospek pemformalkan automatik model bahasa besar mempunyai keupayaan yang cukup baik untuk memformalkan matematik bahasa semula jadi dalam prover teorem interaktif.
Rajah 1 di bawah ialah contoh sempurna pemformalkan automatik. Model bukan sahaja menukar kod Isabelle yang betul secara sintaksis, ia juga mampu menangkap titik penaakulan penting dalam bahasa semula jadi.

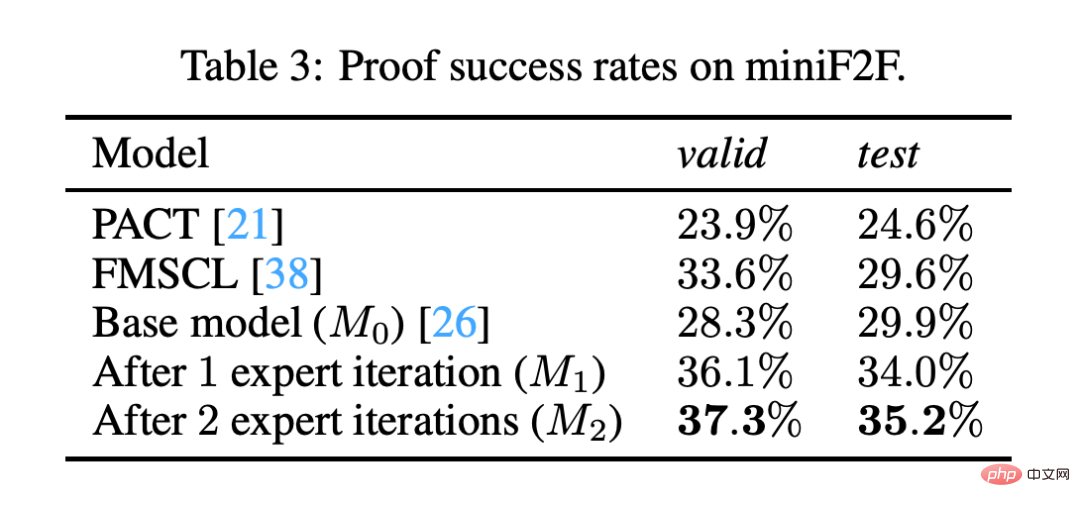
Untuk menguji keberkesanan prosedur pemformalan automatik ini, pasukan itu kemudiannya menggunakan Codex kepada satu set masalah yang sudah mempunyai versi rasmi manusia, yang mana Codex turut dijana Dibangunkan versi rasminya sendiri. Pasukan itu menggunakan AI lain yang dipanggil MiniF2F untuk menyelesaikan kedua-dua versi masalah.
Memformalkan masalah secara automatik meningkatkan kadar kejayaan MiniF2F daripada 29% kepada 35%, menunjukkan bahawa Codex telah mencapai kemajuan penting dalam pemformalkan masalah.
Perlu diperhatikan bahawa pembentangan untuk banyak pertandingan matematik cenderung berbentuk: seseorang diminta untuk mencari jawapan kepada masalah tertentu, dan bukannya membuktikan cadangan yang diberikan . Walau bagaimanapun, pernyataan matematik formal adalah dalam bentuk proposisi, bukan soalan.
Untuk menukar soalan kepada cadangan, penyelidik melampirkan "Jawapan Akhir" selepas soalan:

untuk pemformalkan automatik Format segera ialah :

Adakah AI akan bersaing dengan ahli matematik manusia?
Ini adalah perkembangan yang menarik, tetapi Wu berkata kerja pasukan hanyalah bukti konsep. "Jika matlamatnya adalah untuk melatih mesin yang setanding dengan ahli matematik manusia terbaik, maka pemformalkan automatik nampaknya menjadi laluan utama untuk mencapai matlamat ini." berkata jika kadar kejayaan dipertingkatkan lagi, AI akan mampu bersaing dengan ahli matematik manusia. "
Jika kami mencapai 100%, kami pasti akan mencipta ejen AI yang memenangi pingat emas Olimpik Matematik Antarabangsa."Matlamat segera pasukan adalah untuk menambah baik model formal automatik dan bukti automasi mesin, tetapi kesan masa depan hasil penyelidikan akan menjadi jauh lebih mendalam. Wu berkata model ini boleh mendedahkan bidang matematik yang kini tidak diketahui oleh manusia.
Keupayaan penaakulan mesin ini juga sangat sesuai untuk tugas pengesahan dalam julat bidang yang lebih luas. "Anda boleh mengesahkan sama ada perisian melakukan apa yang anda mahukan, atau anda boleh mengesahkan cip perkakasan, supaya ia mempunyai aplikasi dalam algoritma perdagangan kewangan dan reka bentuk perkakasan
Menggunakan mesin untuk meneroka matematik adalah sesuatu yang teruja. perkembangan itu, kata Yang-Hui He dari Institut Sains Matematik di London, tetapi cabaran sebenar adalah menggunakan model dalam penyelidikan matematik yang kebanyakannya ditulis dalam LaTex. "Kami hanya menggunakan LaTex kerana ia lancar untuk menaip, tetapi ia adalah bahasa semula jadi dalam erti kata dan mempunyai peraturannya sendiri
Katanya, kerana pengguna boleh menentukan fungsi dan Notasi mereka sendiri, fungsi dan fungsi ini." simbol hanya boleh digunakan dalam satu kertas matematik, yang boleh menjadi rumit untuk rangkaian saraf yang dilatih hanya pada teks biasa.
Atas ialah kandungan terperinci Dengan menukar masalah matematik kepada kod, penyelidikan Google telah meningkatkan ketepatan pembuktian mesin.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Gunakan penyataan padam untuk membersihkan jadual SQL
Apr 09, 2025 pm 03:00 PM
Gunakan penyataan padam untuk membersihkan jadual SQL
Apr 09, 2025 pm 03:00 PM
Ya, pernyataan padam boleh digunakan untuk membersihkan jadual SQL, langkah -langkahnya adalah seperti berikut: Gunakan pernyataan padam: padam dari meja_name; Ganti Table_name dengan nama jadual untuk dibersihkan.
 phpmyadmin mencipta jadual data
Apr 10, 2025 pm 11:00 PM
phpmyadmin mencipta jadual data
Apr 10, 2025 pm 11:00 PM
Untuk membuat jadual data menggunakan phpmyadmin, langkah -langkah berikut adalah penting: Sambungkan ke pangkalan data dan klik tab baru. Namakan jadual dan pilih enjin penyimpanan (disyorkan innoDB). Tambah butiran lajur dengan mengklik butang Tambah Lajur, termasuk nama lajur, jenis data, sama ada untuk membenarkan nilai null, dan sifat lain. Pilih satu atau lebih lajur sebagai kunci utama. Klik butang Simpan untuk membuat jadual dan lajur.
 Bagaimana untuk menangani pemecahan memori Redis?
Apr 10, 2025 pm 02:24 PM
Bagaimana untuk menangani pemecahan memori Redis?
Apr 10, 2025 pm 02:24 PM
Pemecahan ingatan redis merujuk kepada kewujudan kawasan bebas kecil dalam ingatan yang diperuntukkan yang tidak dapat ditugaskan semula. Strategi mengatasi termasuk: Mulakan semula Redis: Kosongkan memori sepenuhnya, tetapi perkhidmatan mengganggu. Mengoptimumkan struktur data: Gunakan struktur yang lebih sesuai untuk Redis untuk mengurangkan bilangan peruntukan dan siaran memori. Laraskan parameter konfigurasi: Gunakan dasar untuk menghapuskan pasangan nilai kunci yang paling kurang baru-baru ini. Gunakan mekanisme kegigihan: sandarkan data secara teratur dan mulakan semula redis untuk membersihkan serpihan. Pantau penggunaan memori: Cari masalah tepat pada masanya dan ambil langkah.
 Cara Membuat Pangkalan Data Oracle Cara Membuat Pangkalan Data Oracle
Apr 11, 2025 pm 02:33 PM
Cara Membuat Pangkalan Data Oracle Cara Membuat Pangkalan Data Oracle
Apr 11, 2025 pm 02:33 PM
Mewujudkan pangkalan data Oracle tidak mudah, anda perlu memahami mekanisme asas. 1. Anda perlu memahami konsep pangkalan data dan Oracle DBMS; 2. Menguasai konsep teras seperti SID, CDB (pangkalan data kontena), PDB (pangkalan data pluggable); 3. Gunakan SQL*Plus untuk membuat CDB, dan kemudian buat PDB, anda perlu menentukan parameter seperti saiz, bilangan fail data, dan laluan; 4. Aplikasi lanjutan perlu menyesuaikan set aksara, memori dan parameter lain, dan melakukan penalaan prestasi; 5. Beri perhatian kepada ruang cakera, keizinan dan parameter, dan terus memantau dan mengoptimumkan prestasi pangkalan data. Hanya dengan menguasai ia dengan mahir memerlukan amalan yang berterusan, anda boleh benar -benar memahami penciptaan dan pengurusan pangkalan data Oracle.
 Cara Membuat Pangkalan Data Oracle Cara Membuat Pangkalan Data Oracle
Apr 11, 2025 pm 02:36 PM
Cara Membuat Pangkalan Data Oracle Cara Membuat Pangkalan Data Oracle
Apr 11, 2025 pm 02:36 PM
Untuk membuat pangkalan data Oracle, kaedah biasa adalah menggunakan alat grafik DBCA. Langkah -langkah adalah seperti berikut: 1. Gunakan alat DBCA untuk menetapkan DBName untuk menentukan nama pangkalan data; 2. Tetapkan SYSPASSWORD dan SYSTEMPASSWORD kepada kata laluan yang kuat; 3. Tetapkan aksara dan NationalCharacterset ke Al32utf8; 4. Tetapkan MemorySize dan Tablespacesize untuk menyesuaikan mengikut keperluan sebenar; 5. Tentukan laluan logfile. Kaedah lanjutan dibuat secara manual menggunakan arahan SQL, tetapi lebih kompleks dan terdedah kepada kesilapan. Perhatikan kekuatan kata laluan, pemilihan set aksara, saiz dan memori meja makan
 Pantau titisan redis dengan perkhidmatan pengeksport redis
Apr 10, 2025 pm 01:36 PM
Pantau titisan redis dengan perkhidmatan pengeksport redis
Apr 10, 2025 pm 01:36 PM
Pemantauan yang berkesan terhadap pangkalan data REDIS adalah penting untuk mengekalkan prestasi yang optimum, mengenal pasti kemungkinan kesesakan, dan memastikan kebolehpercayaan sistem keseluruhan. Perkhidmatan Pengeksport Redis adalah utiliti yang kuat yang direka untuk memantau pangkalan data REDIS menggunakan Prometheus. Tutorial ini akan membimbing anda melalui persediaan lengkap dan konfigurasi perkhidmatan pengeksport REDIS, memastikan anda membina penyelesaian pemantauan dengan lancar. Dengan mengkaji tutorial ini, anda akan mencapai tetapan pemantauan operasi sepenuhnya
 Apakah parameter konfigurasi memori Redis?
Apr 10, 2025 pm 02:03 PM
Apakah parameter konfigurasi memori Redis?
Apr 10, 2025 pm 02:03 PM
** Parameter teras konfigurasi memori Redis adalah MaxMemory, yang menghadkan jumlah memori yang boleh digunakan oleh Redis. Apabila had ini melebihi, REDIS melaksanakan strategi penghapusan mengikut dasar-dasar MaxMemory, termasuk: noeviction (secara langsung menolak menulis), AllKeys-LRU/Volatile-LRU (dihapuskan oleh LRU), allkeys-rawak-rawak-rawak (dihapuskan oleh penghapusan rawak), dan volatili-volatili-ttl), dan volatili-volatili-ttl (tidak meniru-rawak), dan volatili-ttl (tidak meniminasi volatili), dan volatili-ttl (tidak meniminasi volatili), dan volatili-ttl (tidak meniru-rawak), dan volatili-ttl (eximination-ttl) Parameter lain yang berkaitan termasuk MaxMemory-Samples (kuantiti sampel LRU), RDB-Mampatan
 Cara Menulis Penyataan Pangkalan Data Oracle
Apr 11, 2025 pm 02:42 PM
Cara Menulis Penyataan Pangkalan Data Oracle
Apr 11, 2025 pm 02:42 PM
Inti dari pernyataan Oracle SQL adalah pilih, masukkan, mengemas kini dan memadam, serta aplikasi fleksibel dari pelbagai klausa. Adalah penting untuk memahami mekanisme pelaksanaan di sebalik pernyataan, seperti pengoptimuman indeks. Penggunaan lanjutan termasuk subqueries, pertanyaan sambungan, fungsi analisis, dan PL/SQL. Kesilapan umum termasuk kesilapan sintaks, isu prestasi, dan isu konsistensi data. Amalan terbaik pengoptimuman prestasi melibatkan menggunakan indeks yang sesuai, mengelakkan pilih *, mengoptimumkan di mana klausa, dan menggunakan pembolehubah terikat. Menguasai Oracle SQL memerlukan amalan, termasuk penulisan kod, debugging, berfikir dan memahami mekanisme asas.



