Union-find: struktur data pepohon yang digunakan untuk menyelesaikan beberapa masalah penggabungan dan pertanyaan bagi set bercabang. Sebagai contoh: terdapat n kampung, tanya sama ada terdapat jalan penghubung antara dua kampung, dan hubungkan dua kampung
Dua teras:
Cari: Cari set di mana unsur itu terletak
Kesatuan: Gabungkan set dua elemen menjadi satu set
Pencarian kesatuan
Cari Cepat<.>
Kerumitan masa Kesatuan: O(logn) boleh dioptimumkan kepada O(a(n) )) a(n)
Gunakan tatasusunan untuk melaksanakan struktur pepohon. Subskrip tatasusunan ialah elemen, dan nilai yang disimpan dalam tatasusunan ialah nilai nod induk
rreee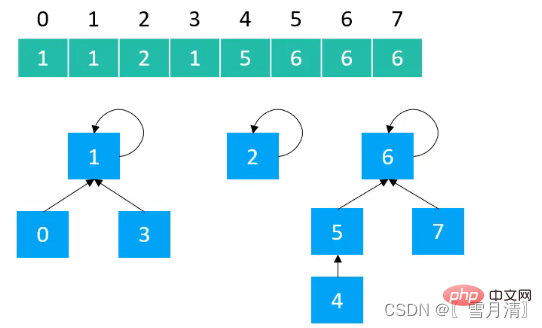 
2.1 Pelaksanaan Carian Pantas
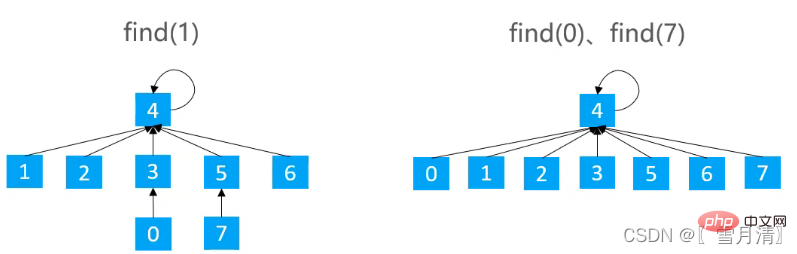
Menggunakan Carian Pantas untuk melaksanakan pencarian kesatuan, ketinggian maksimum pokok ialah 2, dan ketinggian setiap nod ialah Nod induk ialah nod akar
public abstract class UnionFind {
int[] parents;
/**
* 初始化并查集
* @param capacity
*/
public UnionFind(int capacity){
if(capacity < 0) {
throw new IllegalArgumentException("capacity must be >=0");
}
//初始时每一个元素父节点（根结点）是自己
parents = new int[capacity];
for(int i = 0; i < parents.length;i++) {
parents[i] = i;
}
}
/**
* 检查v1 v2 是否属于同一个集合
*/
public boolean isSame(int v1,int v2) {
return find(v1) == find(v2);
}
/**
* 查找v所属的集合 （根节点）
*/
public abstract int find(int v);
/**
* 合并v1 v2 所属的集合
*/
public abstract void union(int v1, int v2);
// 范围检查
public void rangeCheck(int v) {
if(v<0 || v > parents.length)
throw new IllegalArgumentException("v is out of capacity");
}
}
public class UnionFind_QF extends UnionFind {
public UnionFind_QF(int capacity) {
super(capacity);
}
// 查
@Override
public int find(int v) {
rangeCheck(v);
return parents[v];
}
// 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
// 查找v1 v2 的父（根）节点
int p1= find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
for(int i = 0; i< parents.length; i++) {
if(parents[i] == p1) {
parents[i] = p2;
}
}
}
}
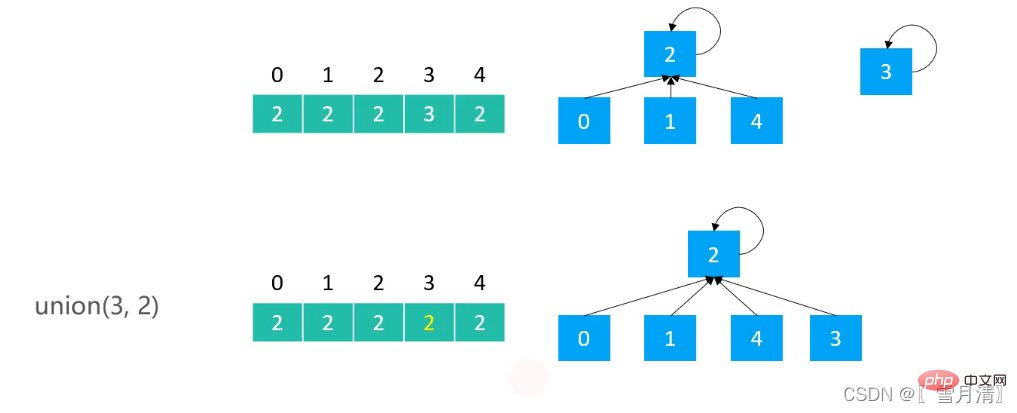
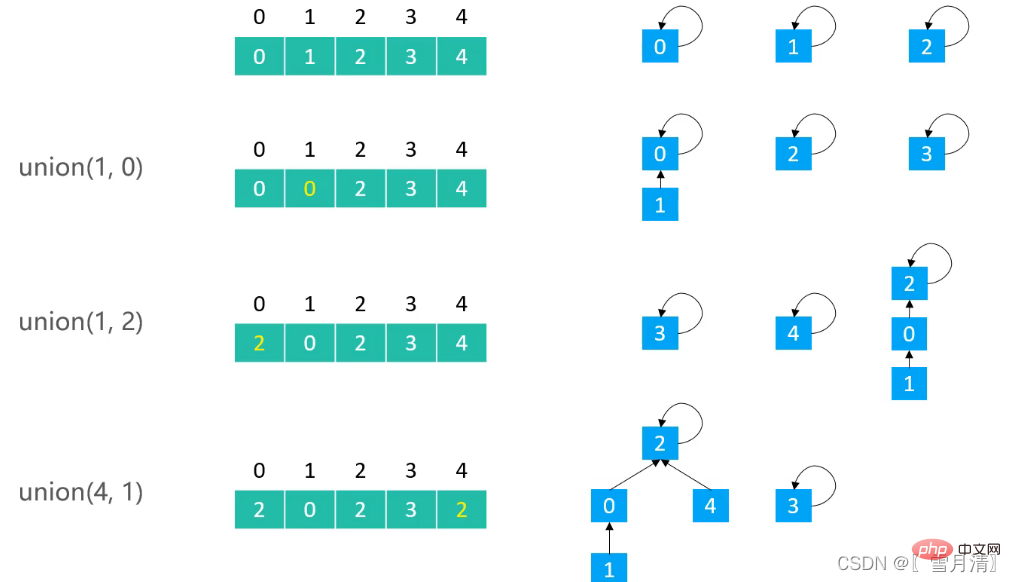Pencarian kesatuan sering dilaksanakan oleh kesatuan pantas, tetapi penyatuan cepat kadangkala menyebabkan ketidakseimbangan pokok
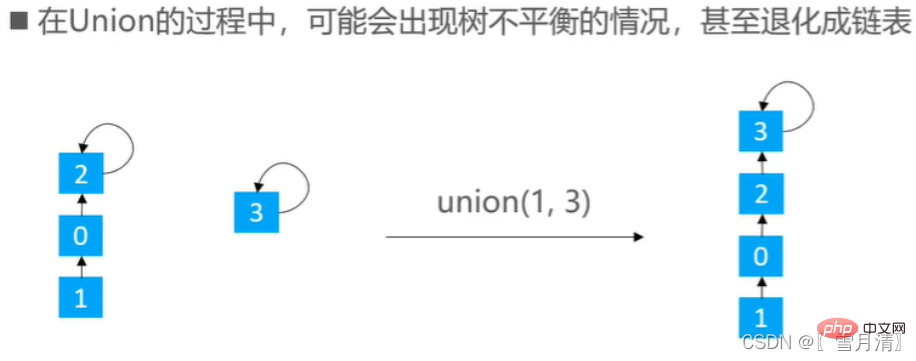3.1 Pengoptimuman berasaskan saiz
Teras idea: cantumkan pokok dengan beberapa elemen kepada pokok dengan banyak elemen
public class UnionFind_QU extends UnionFind {
public UnionFind_QU(int capacity) {
super(capacity);
}
//查某一个元素的根节点
@Override
public int find(int v) {
//检查下标是否越界
rangeCheck(v);
// 一直循环查找节点的根节点
while (v != parents[v]) {
v = parents[v];
}
return v;
}
//V1 并到 v2 中
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
parents[p1] = p2;
}
}3.2 Pengoptimuman berdasarkan pangkat
Idea teras : cantuman pokok pendek ke pokok tinggi
public class UniondFind_QU_S extends UnionFind{
// 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
private int[] sizes;
public UniondFind_QU_S(int capacity) {
super(capacity);
sizes = new int[capacity];
//初始都为 1
for(int i = 0;i < sizes.length;i++) {
sizes[i] = 1;
}
}
@Override
public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
v = parents[v];
}
return v;
}
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
if(sizes[p1] < sizes[p2]) {
parents[p1] = p2;
sizes[p2] += sizes[p1];
// 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
}else {
parents[p2] = p1;
sizes[p1] += sizes[p2];
}
}
}Terdapat tiga idea untuk terus mengoptimumkan: mampatan laluan, pemisahan laluan, separuh laluan
3.2.1 Mampatan Laluan (Mampatan Laluan)
Gunakan apabila mencari Semua nod pada titik laluan ke nod akar, dengan itu mengurangkan ketinggian pokok
public class UnionFind_QU_R extends UnionFind_QU {
// 创建rank数组 ranks[i] 代表以i为根节点的树的高度
private int[] ranks;
public UnionFind_QU_R(int capacity) {
super(capacity);
ranks = new int[capacity];
for(int i = 0;i < ranks.length;i++) {
ranks[i] = 1;
}
}
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
// p1 并到 p2 上 p2为根 树的高度不变
if(ranks[p1] < ranks[p2]) {
parents[p1] = p2;
// p2 并到 p1 上 p1为根 树的高度不变
} else if(ranks[p1] > ranks[p2]) {
parents[p2] = p1;
}else {
// 高度相同 p1 并到 p2上，p2为根 树的高度+1
parents[p1] = p2;
ranks[p2] += 1;
}
}
}
3.2 . Pemisahan 2 Laluan
Jadikan setiap nod pada laluan menghala ke nod datuk neneknya
/**
* Quick Union -基于rank的优化 -路径压缩
*
*/
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
public UnionFind_QU_R_PC(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
if(parents[v] != v) {
//递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
parents[v] = find(parents[v]);
}
return parents[v];
}
}
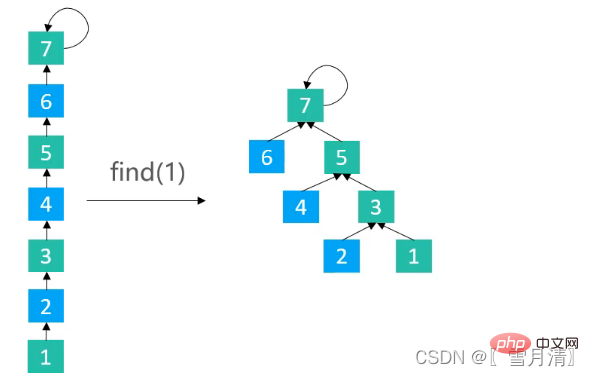
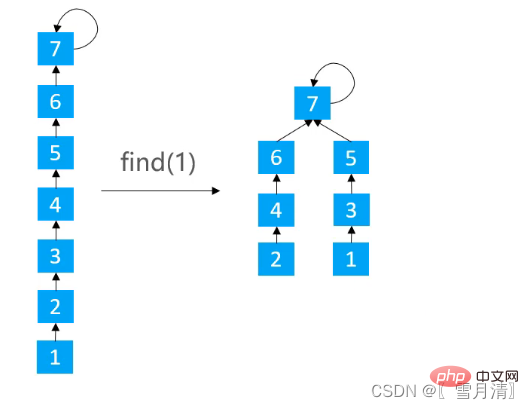Jadikan setiap nod lain pada laluan menghala ke nod datuk neneknya
/**
* Quick Union -基于rank的优化 -路径分裂
*
*/
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
public UnionFind_QU_R_PS(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
while(v != parents[v]) {
int p = parents[v];
parents[v] = parents[parents[v]];
v = p;
}
return v;
}
}
boleh menjamin bahawa kerumitan masa terlunas bagi setiap operasi ialah O(a(n)), a(n)
Atas ialah kandungan terperinci Contoh analisis union-find dalam java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
