
Pokok Rentang: Pokok rentang graf bersambung merujuk kepada subgraf bersambung, yang mengandungi graf Semua n bucu, tetapi hanya cukup n-1 tepi untuk membentuk pokok. Pokok rentang dengan n bucu hanya mempunyai n-1 tepi Jika satu lagi tepi ditambah pada pokok rentang, ia pasti akan membentuk kitaran.
Pokok Rentang Minimum: Di antara semua pokok rentang dalam graf bersambung, berat semua tepi dan pokok rentang terkecil dipanggil pokok rentang minimum.
Dalam kehidupan, struktur grafik adalah yang paling banyak digunakan. Sebagai contoh, dalam pemilihan laluan pembinaan rangkaian komunikasi, kampung boleh dianggap sebagai bucu Jika terdapat laluan komunikasi antara kampung, ia dikira sebagai tepi atau lengkok di antara dua titik nilai berat tepi atau lengkok.
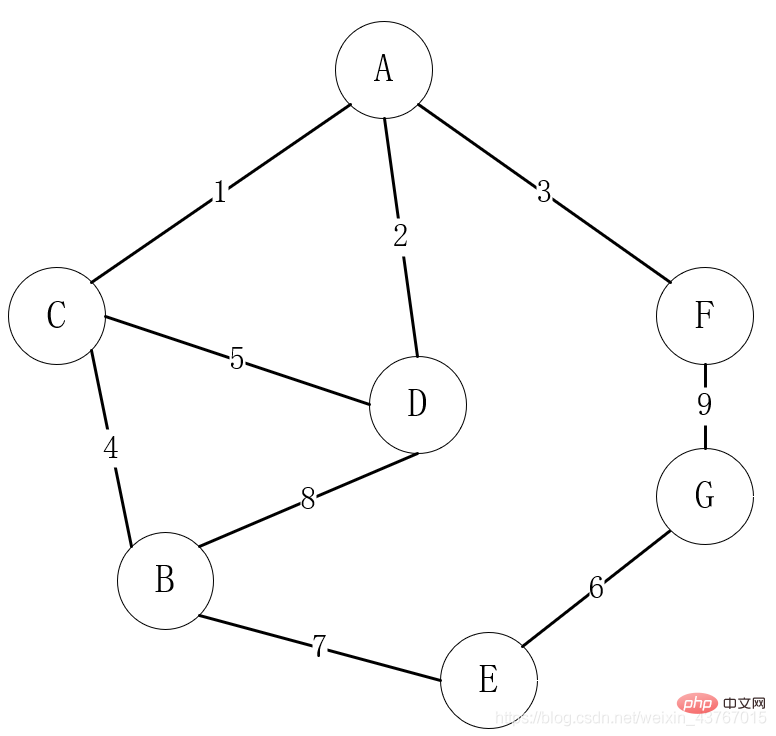
Gambar di atas merupakan kes di mana pilihan laluan pembinaan rangkaian komunikasi dalam kehidupan dipetakan kepada struktur graf. Pucuk berfungsi sebagai kampung Jika terdapat laluan komunikasi antara kampung, ia mempunyai tepi.
Keperluan yang sangat biasa ialah semua kampung yang boleh berkomunikasi mesti berkomunikasi, dan kos pembinaan komunikasi adalah minimum, lagipun dana adalah "terhad", dan dana disimpan, hehe!
Masalah di atas, ditukarkan kepada model matematik, ialah masalah mencari pepohon rentang minimum graf, iaitu: memilih laluan yang menghubungkan semua bucu yang disambungkan dan mempunyai jumlah pemberat terkecil. Terdapat banyak penyelesaian untuk masalah ini, dan dua algoritma yang paling klasik ialah algoritma Prim dan algoritma Kruskal.
Algoritma Prim bermula dari bucu tertentu, dengan mengandaikan bahawa semua bucu tidak bersambung, langkah demi langkah Cari tepi dengan berat terkecil pada setiap bucu untuk menyambung dan membina pokok rentang minimum. Ia menggunakan mata sebagai matlamat untuk membina pokok rentang minimum.
Langkah khusus ialah: Mula-mula pilih bucu a secara rawak, cari semua bucu yang boleh disambungkan ke bucu a, pilih bucu dengan berat rendah untuk disambungkan, kemudian cari semua bucu yang boleh disambungkan kepada kedua-dua ini bucu atau , pilih bucu dengan berat rendah untuk menyambung ke salah satu bucu ulangi proses ini n-1 kali, setiap kali memilih bucu terpendek ke mana-mana bucu hujung yang disambungkan (bukannya bucu terpendek ke bucu pertama) untuk disambungkan; , sehingga Semua bucu disambungkan, dan pokok rentang minimum selesai.
Kes ini sepadan dengan kes dalam kod pelaksanaan di bawah.
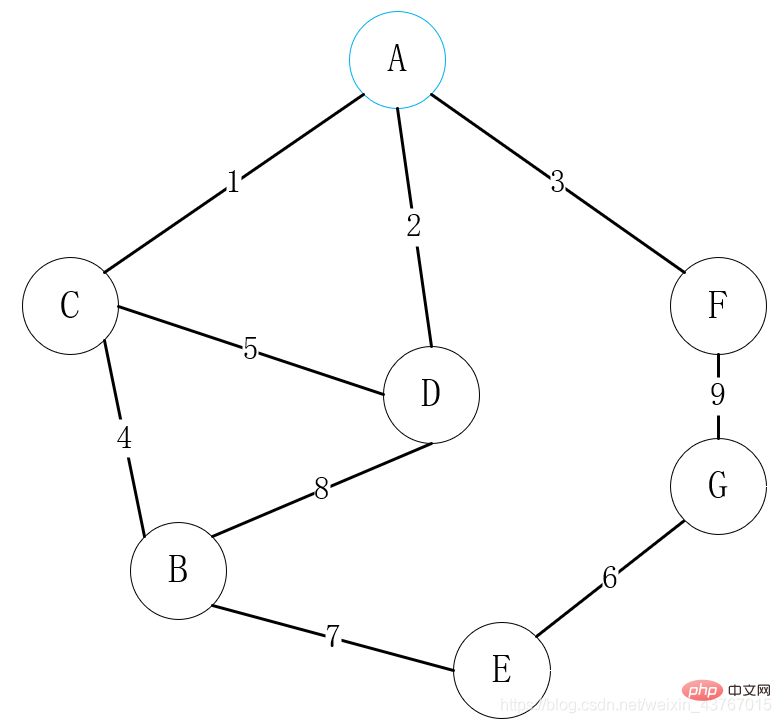
Dalam rajah di atas, mula-mula pilih bucu A sebagai titik bersambung, dapatkan bucu A boleh menyambung semua bucu C, D dan F, dan pilih satu dengan titik rendah berat Bucu disambungkan, di sini pilih A-C
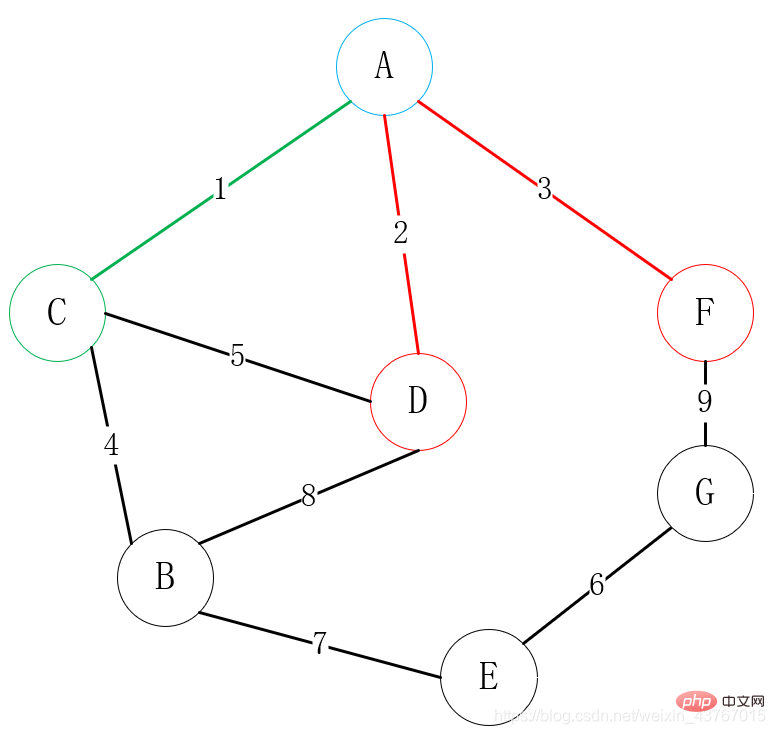
Kemudian cari semua bucu yang boleh disambungkan ke A atau C (tidak termasuk titik bersambung), cari B, D, F, a jumlah Terdapat 4 tepi untuk dipilih, A-D, A-F, C-B, C-D Pilih bucu dengan berat rendah untuk disambungkan dengan salah satu bucu Di sini jelas kita memilih A-D untuk disambungkan
Kemudian cari semua bucu yang boleh disambungkan ke A, C atau D (tidak termasuk titik bersambung), cari B dan F, terdapat 3 tepi untuk dipilih, C-B, D-B, A-F, pilih bucu dengan berat rendah dan salah satu daripadanya Vertices disambungkan, di sini sambungan A-F jelas dipilih; tidak termasuk titik bersambung), cari B , G, terdapat sejumlah 3 tepi untuk dipilih, C-B, D-B, F-G Pilih bucu dengan berat rendah untuk disambungkan dengan salah satu bucu Sambungan C-B jelas dipilih di sini. 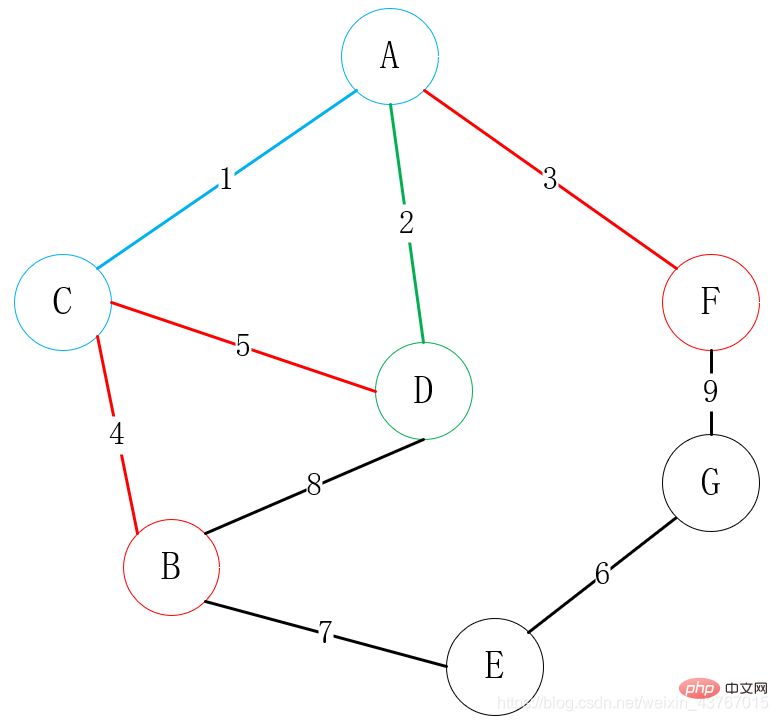
Kemudian cari semua bucu yang boleh disambungkan kepada A atau C atau D atau F atau B (tidak termasuk titik bersambung), cari E dan G, terdapat 2 tepi untuk pilih daripada, B-E, F-G, pilih yang mempunyai berat rendah Puncak disambungkan ke salah satu bucu, di sini sambungan B-E jelas dipilih; bucu yang boleh disambungkan ke A atau C atau D atau F atau B atau E (tidak termasuk titik Bersambung), cari G, terdapat 2 tepi untuk dipilih, E-G, F-G, pilih bucu dengan berat rendah untuk disambungkan dengan salah satu bucu, jelas pilih sambungan E-G di sini; 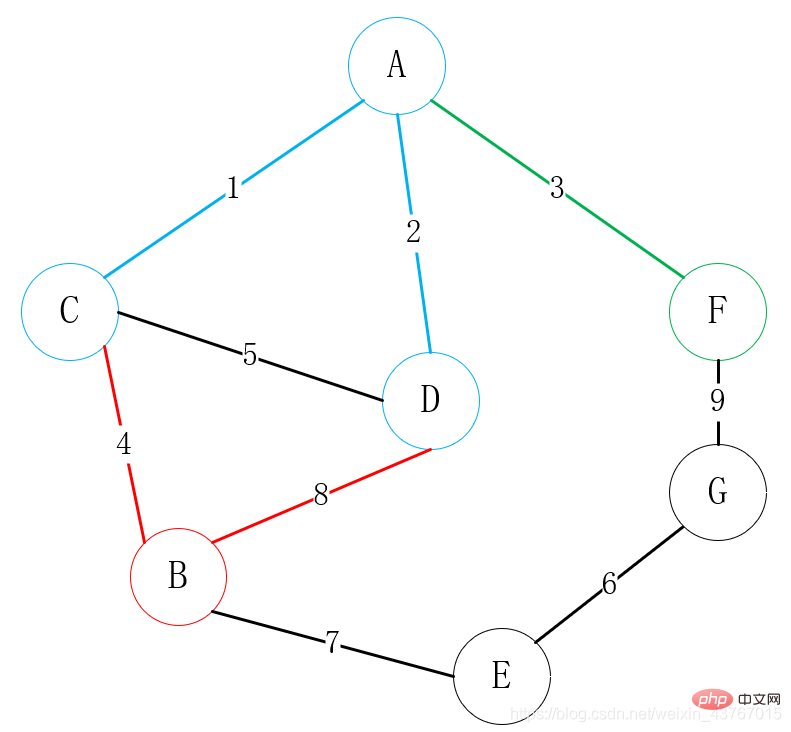
Semua bucu disambungkan pada masa ini, pokok rentang minimum telah dibina, dan berat minimum ialah 23. 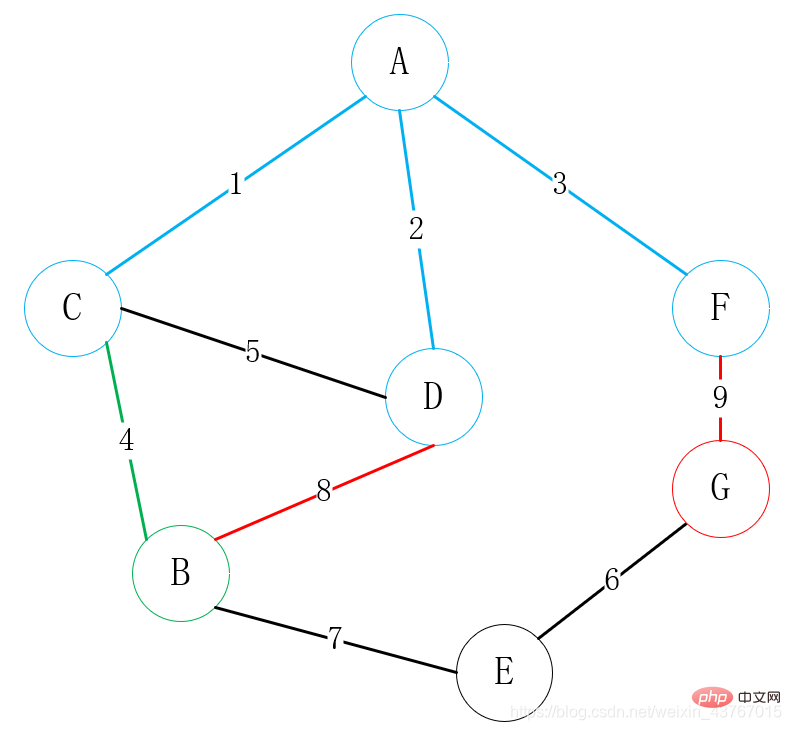
Algoritma Kruskal (Kruskal) secara beransur-ansur membina pokok rentang minimum dengan cara yang semakin meningkat berdasarkan pemberat tepi, iaitu Gunakan tepi sebagai sasaran untuk membina pokok rentang minimum.
Langkah-langkah khusus ialah: Anggap setiap bucu graf berwajaran sebagai hutan, kemudian susun pemberat setiap tepi bersebelahan dalam graf dalam tertib menaik, dan kemudian ekstrak daripada senarai tepi bersebelahan yang disusun Untuk tepi dengan pemberat terkecil, tulis bucu permulaan dan akhir tepi, sambung bucu untuk membentuk hutan menjadi pokok, kemudian baca tepi bersebelahan bucu permulaan dan tamat, ekstrak tepi bersebelahan dengan pemberat kecil dahulu, dan teruskan menyambung bucu untuk membentuk hutan. Keperluan untuk menambah tepi bersebelahan ialah tepi bersebelahan yang ditambahkan pada graf tidak membentuk kitaran (cincin). Ini diulang sehingga n-1 tepi telah ditambah. Pada ketika ini, pokok rentang minimum dibina.
Kes ini sepadan dengan kes dalam kod pelaksanaan di bawah Proses algoritma Kruskal tradisional adalah seperti berikut:
Mula-mula dapatkan tatasusunan set tepi dan kurangkan. ia mengikut berat untuk Untuk mengisih, saya menggunakan isihan secara langsung untuk mengisih dalam kod, atau saya boleh melaksanakan pengisihan timbunan sendiri. , to=C, weight=1 }
Edge{from=D, to=A, weight=2}Edge{from=A, to=F, weight=3}Edge{from= B, to=C, weight= 4}
Edge{from=C, to=D, weight=5}
Edge{from=E, to=G, weight=6}
Edge{ from =E, hingga=B, berat =7}
Tepi{dari=D, hingga=B, berat=8}
Tepi{dari=F, hingga=G, berat=9}
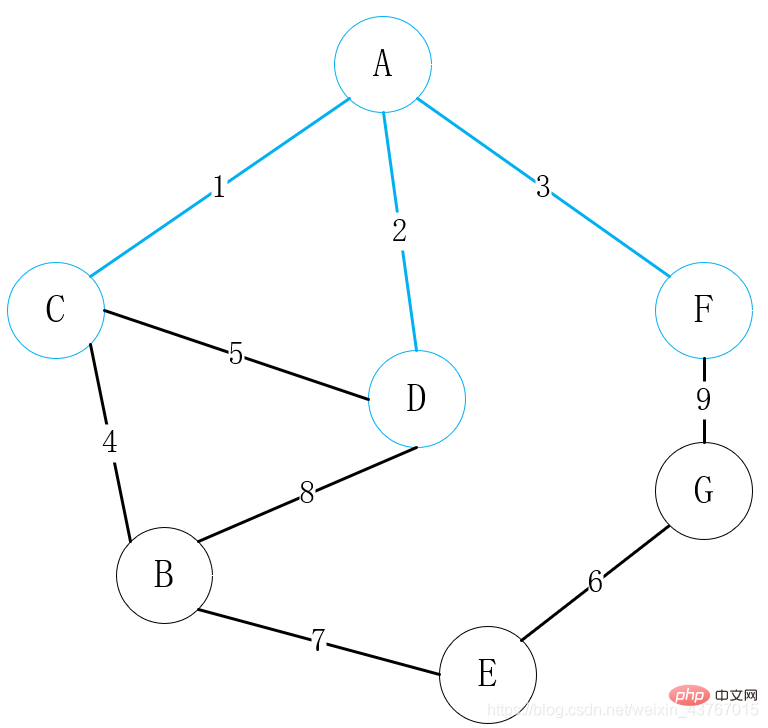
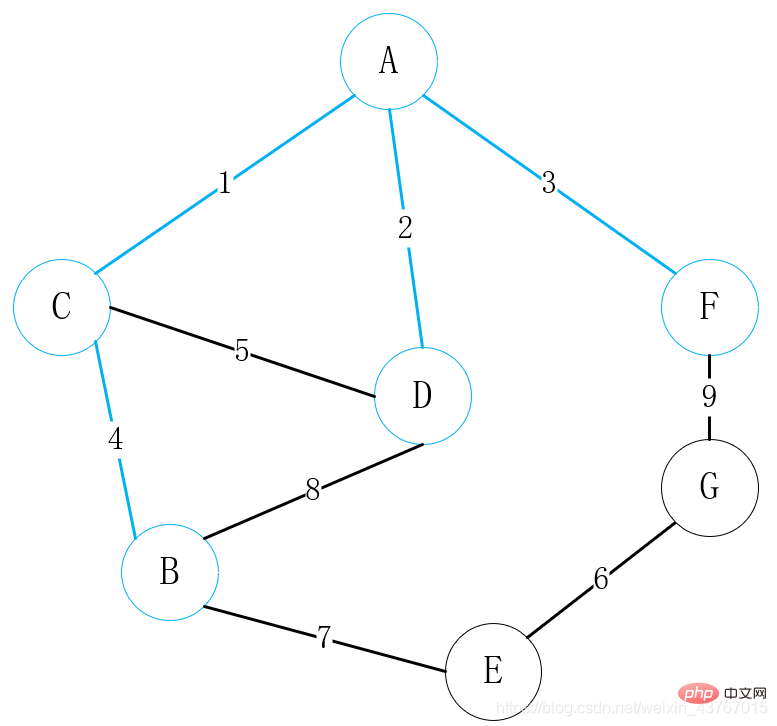
Gelung keluar 1st Edge A-C, nilaikan bahawa ia tidak akan membentuk kitaran dengan pokok rentang minimum yang ditemui, tambahkan jumlah berat sebanyak 1, dan teruskan
gelung keluar D-A tepi kedua, hakim dan Pokok rentang minimum yang telah dijumpai tidak akan membentuk kitaran, dan jumlah pemberat ditambah sebanyak 2. Teruskan; 🎜> Lingkarkan tepi ketiga A-F dan nilaikan ia sama dengan pokok rentang minimum yang telah ditemui A kitaran tidak akan terbentuk, dan jumlah nilai berat meningkat sebanyak 3. Teruskan; 🎜>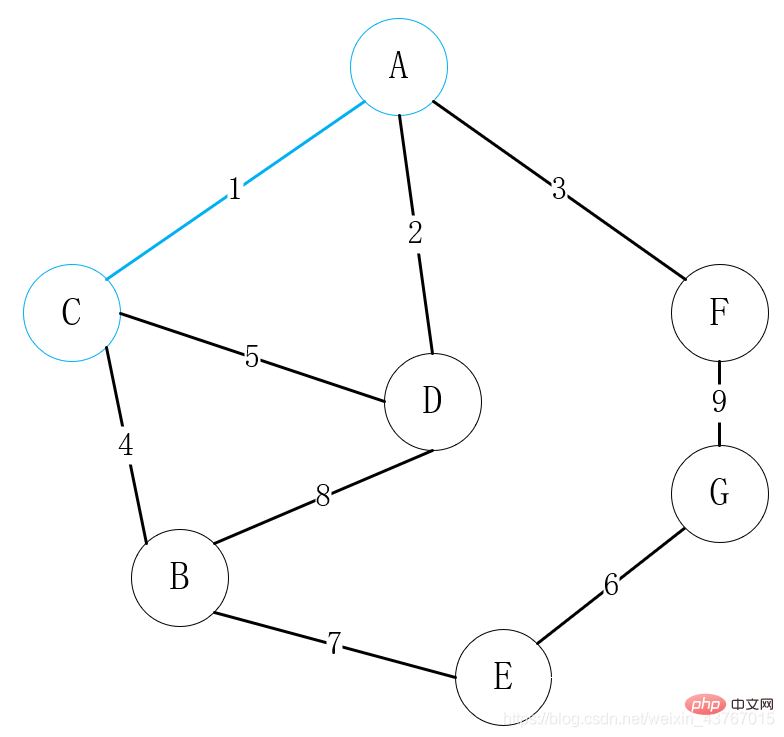
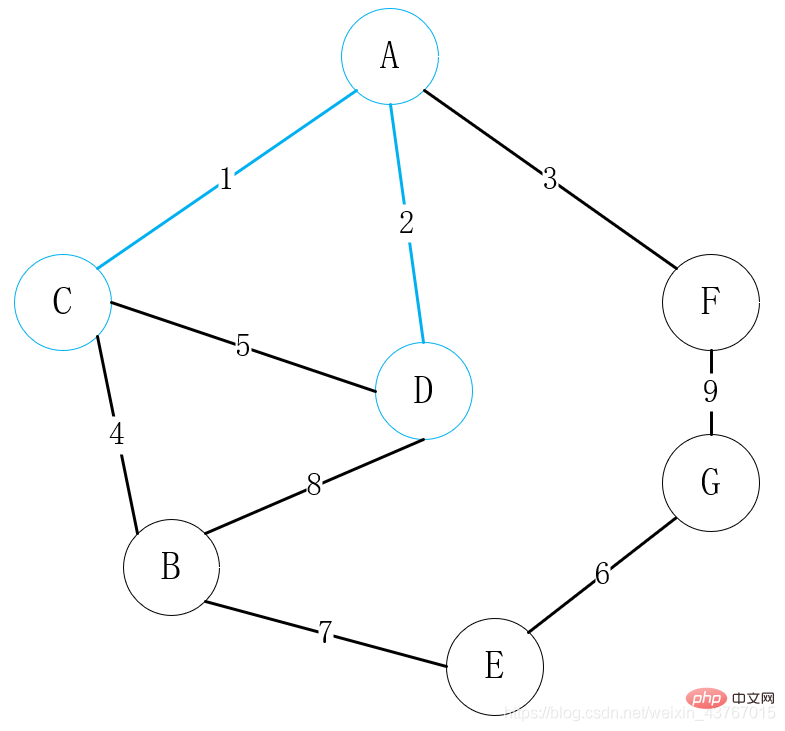
 4 Perlaksanaan Graf Berwajaran Matriks Bersebelahan
4 Perlaksanaan Graf Berwajaran Matriks Bersebelahan
Pelaksanaan di sini boleh membina kelas yang melaksanakan graf berwajaran tidak terarah berdasarkan matriks bersebelahan, dan menyediakan kaedah traversal pertama mendalam dan kaedah lintasan pertama lebar, dan menyediakan perolehan tepi Kaedah tatasusunan set menyediakan dua kaedah mencari pokok rentang minimum, Prim dan Kruskal.
/**
* 无向加权图邻接矩阵实现
* {@link MatrixPrimAndKruskal#MatrixPrimAndKruskal(E[], Edge[])} 构建无向加权图
* {@link MatrixPrimAndKruskal#DFS()} 深度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#BFS()} 广度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#toString()} 输出无向加权图
* {@link MatrixPrimAndKruskal#prim()} Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskal()} Kruskal算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskalAndPrim()} Kruskal算法结合Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#getEdges()} 获取边集数组
*
* @author lx
* @date 2020/5/14 18:13
*/
public class MatrixPrimAndKruskal<E> {
/**
* 顶点数组
*/
private Object[] vertexs;
/**
* 邻接矩阵
*/
private int[][] matrix;
/**
*
*/
private Edge<E>[] edges;
/**
* 由于是加权图,这里设置一个边的权值上限,任何边的最大权值不能大于等于该值,在实际应用中,该值应该根据实际情况确定
*/
private static final int NO_EDGE = 99;
/**
* 边对象,具有权值,在构建加权无向图时使用
*/
private static class Edge<E> {
private E from;
private E to;
private int weight;
public Edge(E from, E to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
/**
* 创建无向加权图
*
* @param vertexs 顶点数组
* @param edges 边对象数组
*/
public MatrixPrimAndKruskal(Object[] vertexs, Edge<E>[] edges) {
//初始化边数组
this.edges = edges;
// 初始化顶点数组,并添加顶点
this.vertexs = Arrays.copyOf(vertexs, vertexs.length);
// 初始化边矩阵,并预先填充边信息
this.matrix = new int[vertexs.length][vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
if (i == j) {
this.matrix[i][j] = 0;
} else {
this.matrix[i][j] = NO_EDGE;
}
}
}
for (Edge<E> edge : edges) {
// 读取一条边的起始顶点和结束顶点索引值
int p1 = getPosition(edge.from);
int p2 = getPosition(edge.to);
//对称的两个点位都置为edge.weight,无向图可以看作相互可达的有向图
this.matrix[p1][p2] = edge.weight;
this.matrix[p2][p1] = edge.weight;
}
}
/**
* 获取某条边的某个顶点所在顶点数组的索引位置
*
* @param e 顶点的值
* @return 所在顶点数组的索引位置, 或者-1 - 表示不存在
*/
private int getPosition(E e) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == e) {
return i;
}
}
return -1;
}
/**
* 深度优先搜索遍历图,类似于树的前序遍历,
*/
public void DFS() {
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("DFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
DFS(i, visited);
}
}
System.out.println();
}
/**
* 深度优先搜索遍历图的递归实现,类似于树的先序遍历
* 因此模仿树的先序遍历,同样借用栈结构,这里使用的是方法的递归,隐式的借用栈
*
* @param i 顶点索引
* @param visited 访问标志数组
*/
private void DFS(int i, boolean[] visited) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
// 遍历该顶点的所有邻接点。若该邻接点是没有访问过,那么继续递归遍历领接点
for (int w = firstVertex(i); w >= 0; w = nextVertex(i, w)) {
if (!visited[w]) {
DFS(w, visited);
}
}
}
/**
* 广度优先搜索图,类似于树的层序遍历
* 因此模仿树的层序遍历,同样借用队列结构
*/
public void BFS() {
// 辅组队列
Queue<Integer> indexLinkedList = new LinkedList<>();
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("BFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
indexLinkedList.add(i);
}
if (!indexLinkedList.isEmpty()) {
//j索引出队列
Integer j = indexLinkedList.poll();
//继续访问j的邻接点
for (int k = firstVertex(j); k >= 0; k = nextVertex(j, k)) {
if (!visited[k]) {
visited[k] = true;
System.out.print(vertexs[k] + " ");
//继续入队列
indexLinkedList.add(k);
}
}
}
}
System.out.println();
}
/**
* 返回顶点v的第一个邻接顶点的索引,失败则返回-1
*
* @param v 顶点v在数组中的索引
* @return 返回顶点v的第一个邻接顶点的索引,失败则返回-1
*/
private int firstVertex(int v) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 从i=0开始*/
for (int i = 0; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 返回顶点v相对于w的下一个邻接顶点的索引,失败则返回-1
*
* @param v 顶点索引
* @param w 第一个邻接点索引
* @return 返回顶点v相对于w的下一个邻接顶点的索引,失败则返回-1
*/
private int nextVertex(int v, int w) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1) || w < 0 || w > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 由于邻接点w的索引已经获取了,所以从i=w+1开始寻找*/
for (int i = w + 1; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 输出图
*
* @return 输出图字符串
*/
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
stringBuilder.append(matrix[i][j]).append("\t");
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
/**
* Prim算法求最小生成树
*/
public void prim() {
System.out.println("prim: ");
//对应节点应该被连接的前驱节点,用来输出
//默认为0,即前驱结点为第一个节点
int[] mid = new int[matrix.length];
//如果某顶点作为末端顶点被连接,对应位置应该为true
//第一个顶点默认被连接
boolean[] connected = new boolean[matrix.length];
connected[0] = true;
//存储未连接顶点到已连接顶点的最短距离(最小权)
int[] dis = new int[matrix.length];
//首先将矩阵第一行即其他顶点到0索引顶点的权值拷贝进去
System.arraycopy(matrix[0], 0, dis, 0, matrix.length);
//存储路径长度
int sum = 0;
//最小权值
int min;
/*默认第一个顶点已经找到了,因此最多还要需要大循环n-1次*/
for (int k = 1; k < matrix.length; k++) {
min = NO_EDGE;
//最小权值的顶点的索引
int minIndex = 0;
/*寻找权值最小的且未被连接的顶点索引*/
for (int i = 1; i < matrix.length; i++) {
//排除已连接的顶点,排除权值等于0的值,这里权值等于0表示已生成的最小生成树的顶点都未能与该顶点连接
if (!connected[i] && dis[i] != 0 && dis[i] < min) {
min = dis[i];
minIndex = i;
}
}
//如果没找到,那么该图可能不是连通图,直接返回了,此时最小生成树没啥意义
if (minIndex == 0) {
return;
}
//权值和增加
sum += min;
//该新连接顶点对应的索引值变成true,表示已被连接,后续判断时跳过该顶点
connected[minIndex] = true;
//输出对应的前驱顶点到该最小顶点的权值
System.out.println(vertexs[mid[minIndex]] + " ---> " + vertexs[minIndex] + " 权值:" + min);
/*在新顶点minIndex加入之前的其他所有顶点到连接顶点最小的权值已经计算过了
因此只需要更新其他未连接顶点到新连接顶点minIndex是否还有更短的权值,有的话就更新找到距离已连接的顶点权最小的顶点*/
for (int i = 1; i < matrix.length; i++) {
//如果该顶点未连接
if (!connected[i]) {
/*如果新顶点到未连接顶点i的权值不为0,并且比原始顶点到未连接顶点i的权值还要小,那么更新对应位置的最小权值*/
if (matrix[minIndex][i] != 0 && dis[i] > matrix[minIndex][i]) {
//更新最小权值
dis[i] = matrix[minIndex][i];
//更新前驱节点索引为新加入节点索引
mid[i] = minIndex;
}
}
}
}
System.out.println("sum: " + sum);
}
/**
* Kruskal算法求最小生成树传统实现,要求知道边集数组,和顶点数组
*/
public void kruskal() {
System.out.println("Kruskal: ");
//由于创建图的时候保存了边集数组,这里直接使用就行了
//Edge[] edges = getEdges();
//this.edges=edges;
//对边集数组进行排序
Arrays.sort(this.edges, Comparator.comparingInt(o -> o.weight));
// 用于保存已有最小生成树中每个顶点在该最小树中的最终终点的索引
int[] vends = new int[this.edges.length];
//能够知道终点索引范围是[0,this.edges.length-1],因此填充edges.length表示没有终点
Arrays.fill(vends, this.edges.length);
int sum = 0;
for (Edge<E> edge : this.edges) {
// 获取第i条边的起点索引from
int from = getPosition(edge.from);
// 获取第i条边的终点索引to
int to = getPosition(edge.to);
// 获取顶点from在"已有的最小生成树"中的终点
int m = getEndIndex(vends, from);
// 获取顶点to在"已有的最小生成树"中的终点
int n = getEndIndex(vends, to);
// 如果m!=n,意味着没有形成环路,则可以添加,否则直接跳过,进行下一条边的判断
if (m != n) {
//添加设置原始终点索引m在已有的最小生成树中的终点为n
vends[m] = n;
System.out.println(vertexs[from] + " ---> " + vertexs[to] + " 权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("sum: " + sum);
//System.out.println(Arrays.toString(this.edges));
}
/**
* 获取顶点索引i的终点如果没有终点则返回顶点索引本身
*
* @param vends 顶点在最小生成树中的终点
* @param i 顶点索引
* @return 顶点索引i的终点如果没有终点则返回顶点索引本身
*/
private int getEndIndex(int[] vends, int i) {
//这里使用循环查找的逻辑,寻找的是最终的终点
while (vends[i] != this.edges.length) {
i = vends[i];
}
return i;
}
/**
* 如果没有现成的边集数组,那么根据邻接矩阵结构获取图中的边集数组
*
* @return 图的边集数组
*/
private Edge[] getEdges() {
List<Edge> edges = new ArrayList<>();
/*遍历矩阵数组 只需要遍历一半就行了*/
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
//如果存在边
if (matrix[i][j] != NO_EDGE && matrix[i][j] != 0) {
edges.add(new Edge<>(vertexs[i], vertexs[j], matrix[i][j]));
//edges[index++] = new Edge(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges.toArray(new Edge[0]);
}
/**
* Kruskal结合Prim算法.不需要知道边集,只需要矩阵数组,和顶点数组
* 同样是求最小权值的边,但是有一个默认起点顶点,该起点可以是要求[0,顶点数量-1]之间的任意值,同时查找最小权的边。
* 可能会有Bug,目前未发现
*/
public void kruskalAndPrim() {
System.out.println("kruskalAndPrim: ");
//已经找到的边携带的顶点对应的索引将变为true,其余未找到边对应的顶点将是false
boolean[] connected = new boolean[matrix.length];
//这里选择第一个顶点为起点,表示以该顶点开始寻找包含该顶点的最小边
connected[0] = true;
int sum = 0, n1 = 0, n2 = 0;
//最小权值
int min;
while (true) {
min = NO_EDGE;
/*找出所有带有已找到顶点的边中,最小权值的边,只需要寻找对称矩阵的一半即可*/
//第一维
for (int i = 0; i < matrix.length; i++) {
//第二维
for (int j = i + 1; j < matrix.length; j++) {
//排除等于0的,排除两个顶点都找到了的,这里实际上已经隐含了排除环的逻辑,如果某条边的两个顶点都找到了,那么如果算上该条边,肯定会形成环
//寻找剩下的最小的权值的边
if (matrix[i][j] != 0 && connected[i] != connected[j] && matrix[i][j] < min) {
min = matrix[i][j];
n1 = i;
n2 = j;
}
}
}
//如果没找到最小权值,该图可能不是连通图,或者已经寻找完毕,直接返回
if (min == NO_EDGE) {
System.out.println(" sum:" + sum);
return;
}
//已经找到的边对应的两个顶点都置为true
connected[n1] = true;
connected[n2] = true;
//输出找到的边和最小权值
System.out.println(vertexs[n1] + " ---> " + vertexs[n2] + " 权值:" + min);
sum += min;
}
}
public static void main(String[] args) {
//顶点数组
Character[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//边数组,加权值
Edge[] edges = {
new Edge<>('A', 'C', 1),
new Edge<>('D', 'A', 2),
new Edge<>('A', 'F', 3),
new Edge<>('B', 'C', 4),
new Edge<>('C', 'D', 5),
new Edge<>('E', 'G', 6),
new Edge<>('E', 'B', 7),
new Edge<>('D', 'B', 8),
new Edge<>('F', 'G', 9)};
//构建图
MatrixPrimAndKruskal<Character> matrixPrimAndKruskal = new MatrixPrimAndKruskal<Character>(vexs, edges);
//输出图
System.out.println(matrixPrimAndKruskal);
//深度优先遍历
matrixPrimAndKruskal.DFS();
//广度优先遍历
matrixPrimAndKruskal.BFS();
//Prim算法输出最小生成树
matrixPrimAndKruskal.prim();
//Kruskal算法输出最小生成树
matrixPrimAndKruskal.kruskal();
//Kruskal算法结合Prim算法输出最小生成树,可能会有Bug,目前未发现
matrixPrimAndKruskal.kruskalAndPrim();
//获取边集数组
Edge[] edges1 = matrixPrimAndKruskal.getEdges();
System.out.println(Arrays.toString(edges1));
}
}5 Pelaksanaan graf berwajaran senarai bersebelahan 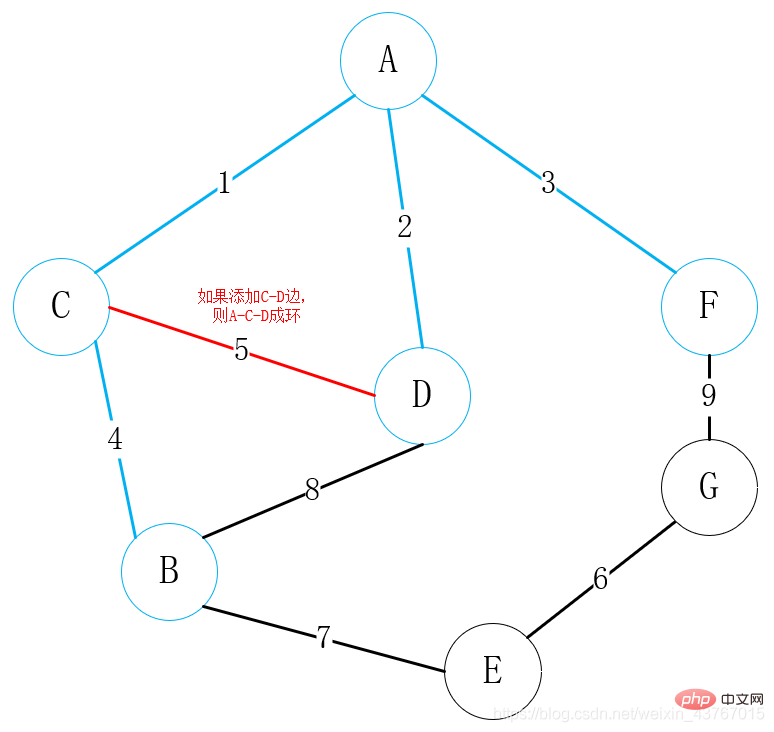
rreeee
Atas ialah kandungan terperinci Bagaimana untuk mencari pokok rentang minimum di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




