
Algoritma pengisihan menggunakan faktor algoritma khusus untuk mengisih satu atau lebih set data mengikut set corak. Urutan akhir dibentangkan mengikut peraturan tertentu.
Dalam menyusun algoritma, kestabilan dan kecekapan adalah isu yang sering kita perlu pertimbangkan.
Kestabilan: Kestabilan bermaksud apabila dua elemen yang sama muncul dalam urutan pada masa yang sama, selepas algoritma pengisihan tertentu, kedudukan relatif kedua-dua elemen sebelum dan selepas pengisihan tidak berubah.
Analisis kerumitan:
(1) Kerumitan masa: iaitu, proses daripada keadaan awal jujukan kepada keadaan hasil diisih akhir selepas operasi seperti transformasi dan peralihan algoritma pengisihan Satu ukuran masa yang dihabiskan.
(2) Kerumitan ruang: Ia adalah overhed ruang yang dibelanjakan dari keadaan awal jujukan melalui proses menyusun transformasi anjakan kepada keadaan akhir.
Algoritma pengisihan biasa dibahagikan kepada jenis berikut:
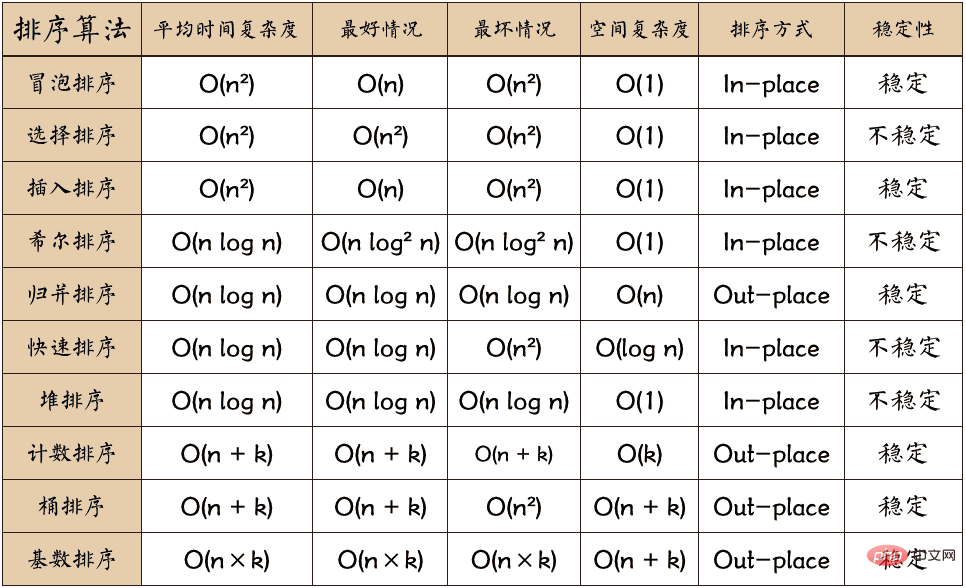
Isih Separuh Sisipan (Isih Sisipan Binari) ialah penambahbaikan pada algoritma isihan sisipan. Masukkan elemen secara berterusan ke dalam urutan yang telah diisih sebelumnya. Memandangkan separuh pertama ialah urutan yang diisih, kita tidak perlu mencari titik sisipan mengikut urutan Kita boleh menggunakan kaedah carian separuh untuk mempercepatkan carian untuk titik sisipan.
Dalam proses memasukkan elemen baharu ke dalam tatasusunan yang diisih, apabila mencari titik sisipan, tetapkan elemen pertama kawasan yang akan disisipkan kepada [rendah], dan elemen terakhir Jika elemen ditetapkan kepada a[tinggi], maka dalam setiap pusingan perbandingan, elemen yang akan dimasukkan akan dibandingkan dengan a[m], di mana m = (rendah+tinggi)/2 lebih kecil daripada elemen rujukan, pilih a[rendah] kepada [m-1] ialah kawasan sisipan baharu (iaitu tinggi=m-1), jika tidak pilih a[m+1] kepada a[tinggi] sebagai kawasan sisipan baharu (iaitu rendah=m+1), dan seterusnya sehingga rendah
Ringkasnya: manfaatkan ciri susunan elemen yang disusun dan gunakan ciri carian binari untuk mencari kedudukan yang hendak dimasukkan dengan cepat.
// Binary Insertion Sort method
private static void binaryInsertSort(int[] array){
for(int i = 1; i < array.length; i++){
int temp = array[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < array[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
array[j] = array[j - 1];
}
array[low] = temp;
}
}Algoritma isihan separuh sisipan ialah algoritma pengisihan yang stabil Ia mengurangkan bilangan perbandingan antara kata kunci dengan ketara berbanding dengan algoritma sisipan langsung, jadi ia lebih pantas daripada sisipan langsung. algoritma isihan. Cepat, tetapi bilangan pergerakan rekod tidak berubah, jadi kerumitan masa algoritma isihan sisipan yang dibelah dua masih O(n^2), yang sama dengan algoritma isihan sisipan langsung.
Kerumitan masa
Kes terbaik: O(n). Jika elemen diisih dalam susunan hadapan, kedudukan akan ditemui terus pada permulaan, tanpa mencari dan beralih.
Kes terburuk: O(n^2). Jika elemen diisih dalam susunan terbalik, carian data diperlukan setiap kali.
Purata kerumitan: O(n^2).
Kerumitan ruang: O(1). Hanya beberapa ruang storan diperlukan untuk merekodkan unit utama maklumat, iaitu, kerumitan ruang ialah O(1).
Contoh:
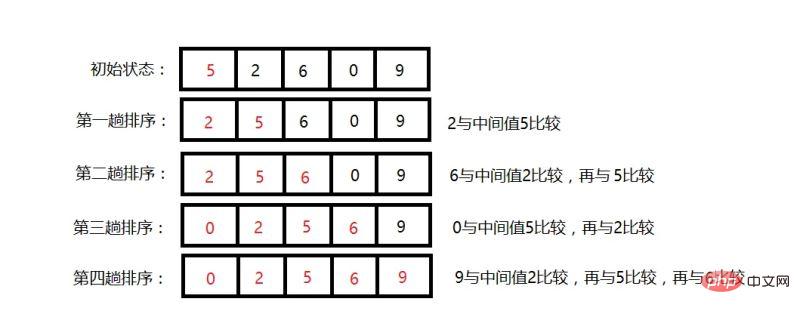
Idea keseluruhan algoritma telah diterangkan di atas perairan itu.
Isih sisipan separuh
Perihalan masalah:
Anda diberi nombor tatasusunan integer, sila susun tatasusunan dalam tertib menaik.
Contoh 1:
Input: nums = [5,2,3,1]
Output: [1,2,3,5]
Contoh 2:
Input: nums = [5,1,1,2,0,0]
Output: [0,0,1,1,2,5]
Petua:
1
-5 * 104 rreeee
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan algoritma isihan separuh sisipan dalam Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




