 pembangunan bahagian belakang
pembangunan bahagian belakang
 Tutorial Python
Tutorial Python
 Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS)
Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS)
Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS)
POCS: Unjuran ke Set Cembung. Dalam matematik, set cembung ialah set di mana mana-mana ruas garis antara mana-mana dua titik berada dalam set. Unjuran ialah operasi memetakan titik ke subruang dalam ruang lain. Memandangkan set cembung dan titik, anda boleh beroperasi dengan mencari unjuran titik ke set cembung. Unjuran ialah titik dalam set cembung yang paling hampir dengan titik dan boleh dikira dengan meminimumkan jarak antara titik ini dan mana-mana titik lain dalam set cembung. Memandangkan ia adalah unjuran, kita boleh memetakan ciri kepada set cembung dalam ruang lain, supaya operasi seperti pengelompokan atau pengurangan dimensi boleh dilakukan.
Artikel ini menyemak algoritma pengelompokan berdasarkan kaedah unjuran set cembung, iaitu algoritma pengelompokan berdasarkan POCS. Kertas asal diterbitkan di IWIS2022.
Set cembung
Set cembung ditakrifkan sebagai satu set titik data, di mana segmen garisan yang menghubungkan mana-mana dua titik x1 dan x2 dalam set disertakan sepenuhnya dalam set ini. Mengikut definisi set cembung, set kosong ∅, set unitari, segmen garis, hyperplane, dan sfera Euclidean semuanya dianggap sebagai set cembung. Titik data juga dianggap sebagai set cembung kerana ia adalah set tunggal (set dengan hanya satu elemen). Ini membuka laluan baharu untuk menggunakan konsep POCS pada titik data berkelompok.
Projection of Convex Sets (POCS)
Kaedah POCS secara kasar boleh dibahagikan kepada dua jenis: berselang-seli dan selari.
1. Poc berselang seli
Bermula dari mana-mana titik dalam ruang data, unjuran berselang-seli dari titik ini kepada dua (atau lebih) set cembung bersilang akan menumpu ke titik persilangan yang ditetapkan Satu titik, contohnya rajah berikut:
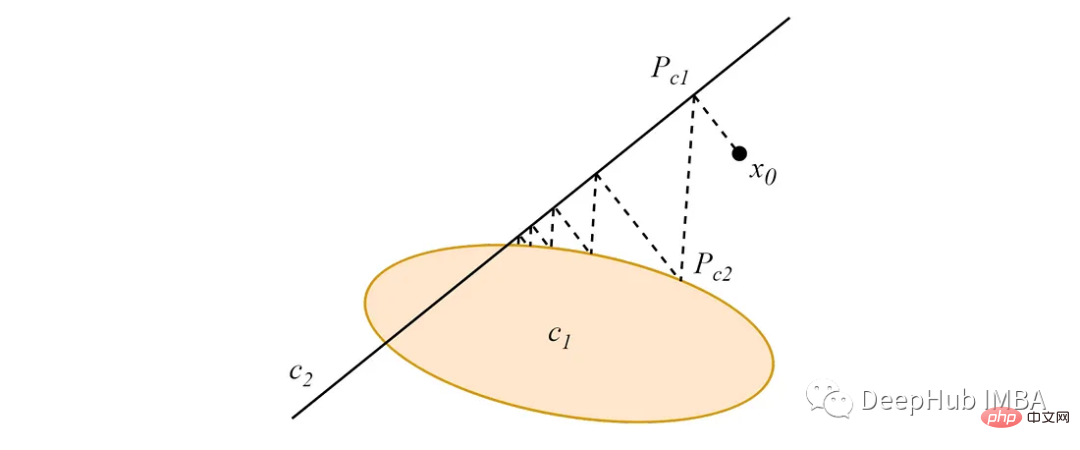
Apabila set cembung tidak bersilang, unjuran berselang-seli akan menumpu kepada kitaran had tamak yang bergantung pada susunan unjuran.
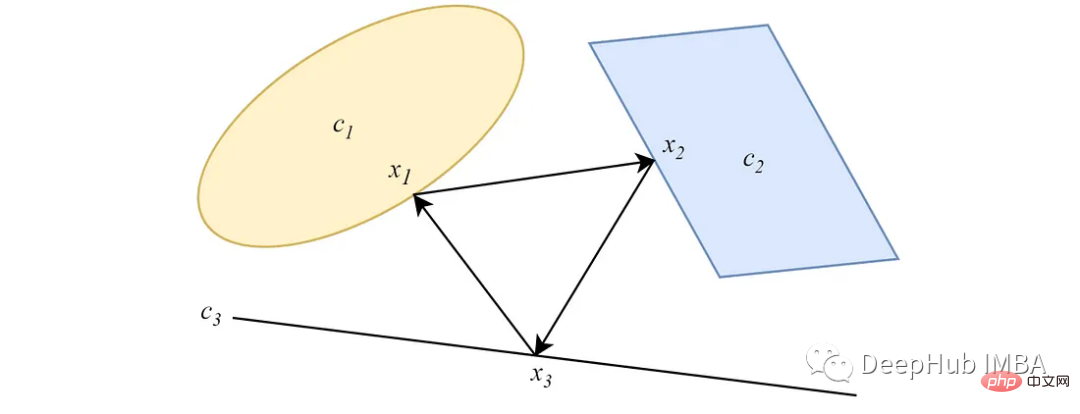
2. POCS Selari
Berbeza daripada bentuk berselang-seli, projek POCS selari dari titik data ke semua set cembung secara serentak, dan setiap unjuran Semua mempunyai kepentingan berat badan. Untuk dua set cembung bersilang yang tidak kosong, serupa dengan versi berselang-seli, unjuran selari menumpu ke satu titik di persimpangan set.
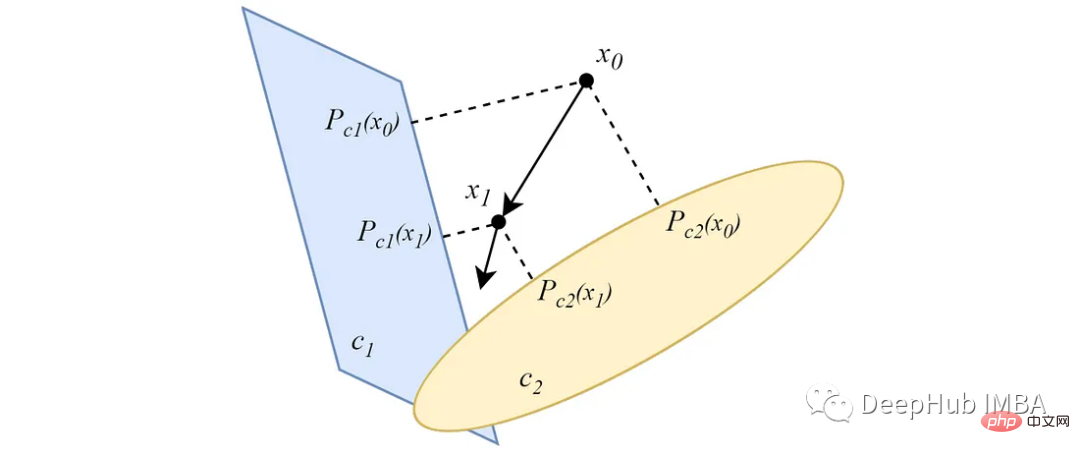
Dalam kes di mana set cembung tidak bersilang, unjuran akan menumpu kepada penyelesaian minimum. Idea utama algoritma pengelompokan berasaskan POC datang daripada ciri ini.
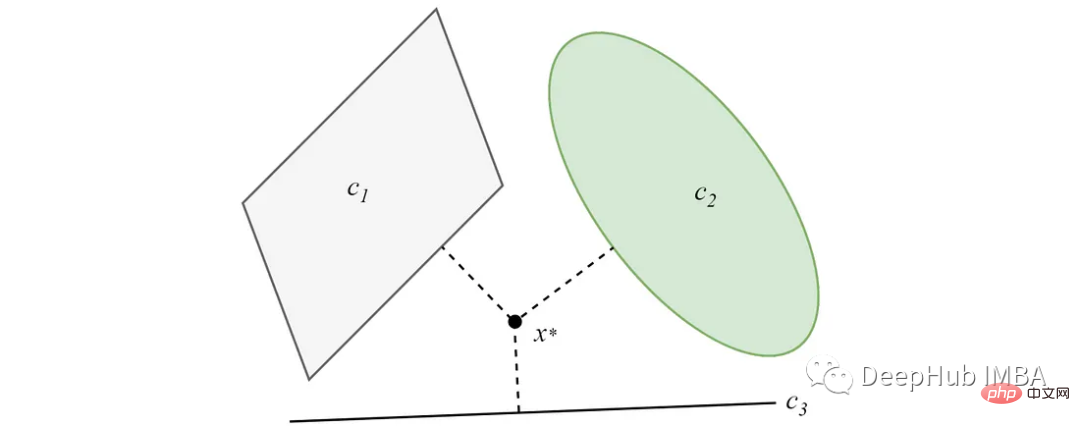
Untuk butiran lanjut tentang POCS, anda boleh melihat kertas asal
Algoritma pengelompokan berasaskan POCS
Menggunakan penumpuan selari Harta kaedah POCS, pengarang kertas itu mencadangkan algoritma pengelompokan yang sangat mudah tetapi berkesan pada tahap tertentu. Algoritma ini berfungsi sama dengan algoritma K-Means klasik, tetapi terdapat perbezaan dalam cara setiap titik data diproses: algoritma K-Means menimbang kepentingan setiap titik data yang sama, tetapi algoritma pengelompokan berasaskan POC Setiap titik data ditimbang secara berbeza dalam kepentingan, yang berkadar dengan jarak titik data daripada prototaip kelompok.
Pseudokod algoritma adalah seperti berikut:

Hasil eksperimen
Pengarang menguji algoritma berasaskan POC pada beberapa penanda aras awam set data Prestasi algoritma pengelompokan. Jadual di bawah meringkaskan perihalan set data ini.
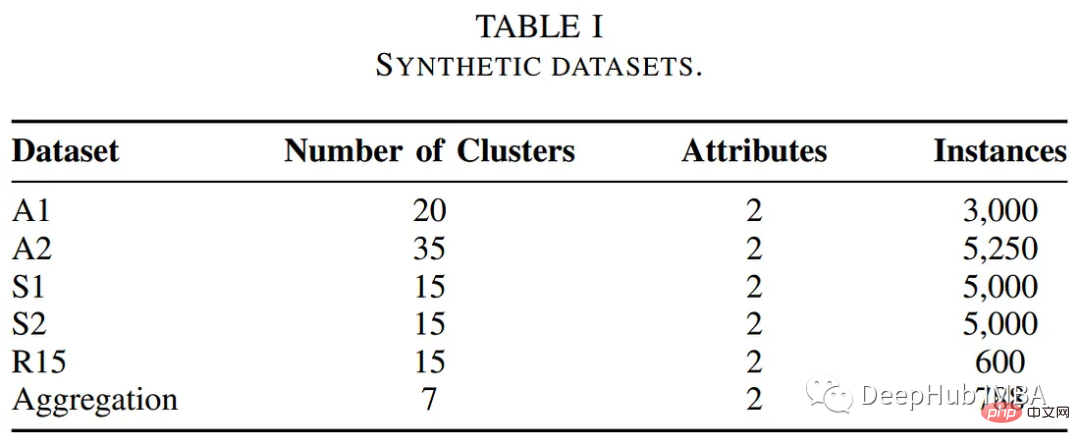
Pengarang membandingkan prestasi algoritma pengelompokan berasaskan POC dengan kaedah pengelompokan tradisional lain, termasuk algoritma k-means dan fuzzy c-means. Jadual berikut meringkaskan penilaian dari segi masa pelaksanaan dan ralat pengelompokan.
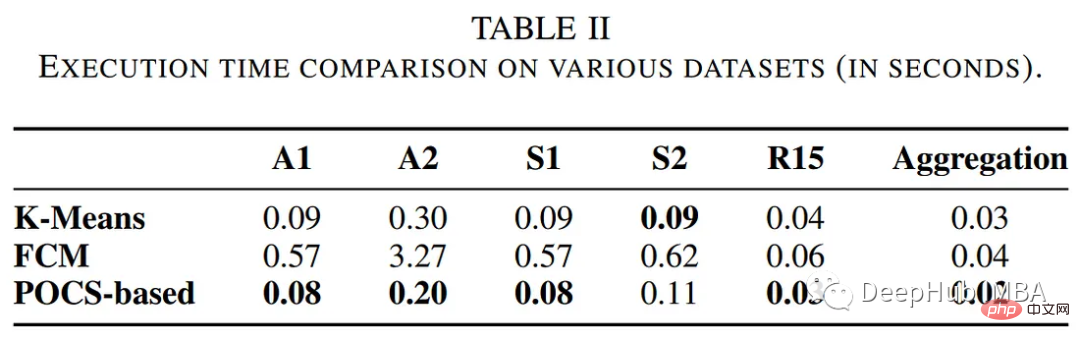
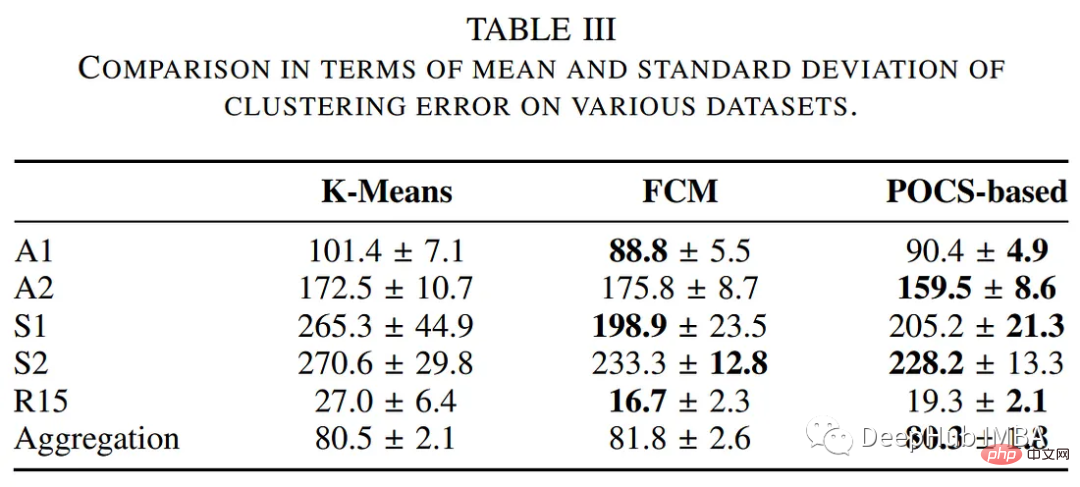
Hasil pengelompokan ditunjukkan di bawah:

Kod sampel
Kami menggunakan algoritma ini pada set data yang sangat mudah. Pengarang telah mengeluarkan pakej untuk kegunaan langsung, yang boleh kita gunakan terus untuk aplikasi:
pip install pocs-based-clustering
Buat set data ringkas 5000 titik data berpusat pada 10 gugusan:
# Import packages import time import matplotlib.pyplot as plt from sklearn.datasets import make_blobs from pocs_based_clustering.tools import clustering # Generate a simple dataset num_clusters = 10 X, y = make_blobs(n_samples=5000, centers=num_clusters, cluster_std=0.5, random_state=0) plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], s=50) plt.show()

Lakukan pengelompokan dan paparkan hasilnya:
# POSC-based Clustering Algorithm centroids, labels = clustering(X, num_clusters, 100) # Display results plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis') plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red') plt.show()

总结
我们简要回顾了一种简单而有效的基于投影到凸集(POCS)方法的聚类技术,称为基于POCS的聚类算法。该算法利用POCS的收敛特性应用于聚类任务,并在一定程度上实现了可行的改进。在一些基准数据集上验证了该算法的有效性。
论文的地址如下:https://arxiv.org/abs/2208.08888
作者发布的源代码在这里:https://github.com/tranleanh/pocs-based-clustering
Atas ialah kandungan terperinci Algoritma pengelompokan berdasarkan unjuran pada set cembung (POCS). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
Ditulis di atas & pemahaman peribadi penulis: Pada masa ini, dalam keseluruhan sistem pemanduan autonomi, modul persepsi memainkan peranan penting Hanya selepas kenderaan pemanduan autonomi yang memandu di jalan raya memperoleh keputusan persepsi yang tepat melalui modul persepsi boleh Peraturan hiliran dan. modul kawalan dalam sistem pemanduan autonomi membuat pertimbangan dan keputusan tingkah laku yang tepat pada masanya dan betul. Pada masa ini, kereta dengan fungsi pemanduan autonomi biasanya dilengkapi dengan pelbagai penderia maklumat data termasuk penderia kamera pandangan sekeliling, penderia lidar dan penderia radar gelombang milimeter untuk mengumpul maklumat dalam modaliti yang berbeza untuk mencapai tugas persepsi yang tepat. Algoritma persepsi BEV berdasarkan penglihatan tulen digemari oleh industri kerana kos perkakasannya yang rendah dan penggunaan mudah, dan hasil keluarannya boleh digunakan dengan mudah untuk pelbagai tugas hiliran.
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Lapisan bawah fungsi C++ sort menggunakan isihan gabungan, kerumitannya ialah O(nlogn), dan menyediakan pilihan algoritma pengisihan yang berbeza, termasuk isihan pantas, isihan timbunan dan isihan stabil.
 Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Konvergensi kecerdasan buatan (AI) dan penguatkuasaan undang-undang membuka kemungkinan baharu untuk pencegahan dan pengesanan jenayah. Keupayaan ramalan kecerdasan buatan digunakan secara meluas dalam sistem seperti CrimeGPT (Teknologi Ramalan Jenayah) untuk meramal aktiviti jenayah. Artikel ini meneroka potensi kecerdasan buatan dalam ramalan jenayah, aplikasi semasanya, cabaran yang dihadapinya dan kemungkinan implikasi etika teknologi tersebut. Kecerdasan Buatan dan Ramalan Jenayah: Asas CrimeGPT menggunakan algoritma pembelajaran mesin untuk menganalisis set data yang besar, mengenal pasti corak yang boleh meramalkan di mana dan bila jenayah mungkin berlaku. Set data ini termasuk statistik jenayah sejarah, maklumat demografi, penunjuk ekonomi, corak cuaca dan banyak lagi. Dengan mengenal pasti trend yang mungkin terlepas oleh penganalisis manusia, kecerdasan buatan boleh memperkasakan agensi penguatkuasaan undang-undang
 Mengapakah sukar untuk melaksanakan fungsi seperti koleksi dalam bahasa Go?
Mar 24, 2024 am 11:57 AM
Mengapakah sukar untuk melaksanakan fungsi seperti koleksi dalam bahasa Go?
Mar 24, 2024 am 11:57 AM
Sukar untuk melaksanakan fungsi seperti koleksi dalam bahasa Go, yang merupakan masalah yang menyusahkan ramai pembangun. Berbanding dengan bahasa pengaturcaraan lain seperti Python atau Java, bahasa Go tidak mempunyai jenis koleksi terbina dalam, seperti set, peta, dll., yang membawa beberapa cabaran kepada pembangun apabila melaksanakan fungsi pengumpulan. Mula-mula, mari kita lihat mengapa sukar untuk melaksanakan fungsi seperti koleksi secara langsung dalam bahasa Go. Dalam bahasa Go, struktur data yang paling biasa digunakan ialah hirisan dan peta Mereka boleh melengkapkan fungsi seperti koleksi, tetapi
 Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
01Garis prospek Pada masa ini, sukar untuk mencapai keseimbangan yang sesuai antara kecekapan pengesanan dan hasil pengesanan. Kami telah membangunkan algoritma YOLOv5 yang dipertingkatkan untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi, menggunakan piramid ciri berbilang lapisan, strategi kepala pengesanan berbilang dan modul perhatian hibrid untuk meningkatkan kesan rangkaian pengesanan sasaran dalam imej penderiaan jauh optik. Menurut set data SIMD, peta algoritma baharu adalah 2.2% lebih baik daripada YOLOv5 dan 8.48% lebih baik daripada YOLOX, mencapai keseimbangan yang lebih baik antara hasil pengesanan dan kelajuan. 02 Latar Belakang & Motivasi Dengan perkembangan pesat teknologi penderiaan jauh, imej penderiaan jauh optik resolusi tinggi telah digunakan untuk menggambarkan banyak objek di permukaan bumi, termasuk pesawat, kereta, bangunan, dll. Pengesanan objek dalam tafsiran imej penderiaan jauh
 Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
1. Latar Belakang Pembinaan 58 Portrait Platform Pertama sekali, saya ingin berkongsi dengan anda latar belakang pembinaan 58 Portrait Platform. 1. Pemikiran tradisional platform pemprofilan tradisional tidak lagi mencukupi Membina platform pemprofilan pengguna bergantung pada keupayaan pemodelan gudang data untuk menyepadukan data daripada pelbagai barisan perniagaan untuk membina potret pengguna yang tepat untuk memahami tingkah laku, minat pengguna dan keperluan, dan menyediakan keupayaan sampingan, akhirnya, ia juga perlu mempunyai keupayaan platform data untuk menyimpan, bertanya dan berkongsi data profil pengguna dan menyediakan perkhidmatan profil dengan cekap. Perbezaan utama antara platform pemprofilan perniagaan binaan sendiri dan platform pemprofilan pejabat pertengahan ialah platform pemprofilan binaan sendiri menyediakan satu barisan perniagaan dan boleh disesuaikan atas permintaan platform pertengahan pejabat berkhidmat berbilang barisan perniagaan, mempunyai kompleks pemodelan, dan menyediakan lebih banyak keupayaan umum. 2.58 Potret pengguna latar belakang pembinaan potret di platform tengah 58
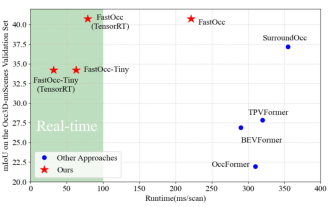 Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Ditulis di atas & Pemahaman peribadi penulis ialah dalam sistem pemanduan autonomi, tugas persepsi adalah komponen penting dalam keseluruhan sistem pemanduan autonomi. Matlamat utama tugas persepsi adalah untuk membolehkan kenderaan autonomi memahami dan melihat elemen persekitaran sekeliling, seperti kenderaan yang memandu di jalan raya, pejalan kaki di tepi jalan, halangan yang dihadapi semasa memandu, tanda lalu lintas di jalan raya, dan sebagainya, dengan itu membantu hiliran. modul Membuat keputusan dan tindakan yang betul dan munasabah. Kenderaan dengan keupayaan pemanduan autonomi biasanya dilengkapi dengan pelbagai jenis penderia pengumpulan maklumat, seperti penderia kamera pandangan sekeliling, penderia lidar, penderia radar gelombang milimeter, dsb., untuk memastikan kenderaan autonomi itu dapat melihat dan memahami persekitaran sekeliling dengan tepat. elemen , membolehkan kenderaan autonomi membuat keputusan yang betul semasa pemanduan autonomi. kepala



