Kerumitan masa Java dan analisis contoh kerumitan ruang
1. Kecekapan algoritma
Analisis kecekapan algoritma dibahagikan kepada dua jenis: yang pertama ialah kecekapan masa, dan yang kedua ialah kecekapan ruang. Kecekapan masa dipanggil kerumitan masa, dan kecekapan ruang dipanggil kerumitan ruang. Kerumitan masa terutamanya mengukur kelajuan berjalan algoritma, manakala kerumitan ruang terutamanya mengukur ruang tambahan yang diperlukan oleh algoritma Pada hari-hari awal pembangunan komputer, kapasiti penyimpanan komputer adalah sangat kecil. Jadi kami sangat mengambil berat tentang kerumitan ruang. Bagaimanapun, selepas perkembangan pesat industri komputer, kapasiti penyimpanan komputer telah mencapai tahap yang sangat tinggi. Jadi kita tidak perlu lagi memberi perhatian khusus kepada kerumitan ruang sesuatu algoritma.
2. Kerumitan masa
1 Konsep kerumitan masa
Masa yang diambil oleh algoritma adalah berkadar dengan bilangan pelaksanaan penyataannya adalah Bilangan pelaksanaan ialah kerumitan masa algoritma. Maksudnya, apabila kita mendapat kod dan melihat kerumitan masa kod itu, kita terutamanya mendapati berapa kali kod dengan penyataan paling banyak dilaksanakan dalam kod itu telah dilaksanakan.
2. Perwakilan asimptotik O Besar
Lihat graf dan analisis:

Apabila nilai N menjadi lebih besar dan lebih besar , 2N dan Nilai 10 boleh diabaikan.
Malah, apabila kita mengira kerumitan masa, kita sebenarnya tidak perlu mengira bilangan eksekusi yang tepat, tetapi hanya anggaran bilangan pelaksanaan, jadi di sini kita menggunakan perwakilan asimptotik Big O.
Tatatanda O Besar: Ia ialah tatatanda matematik yang digunakan untuk menerangkan tingkah laku asimptotik bagi sesuatu fungsi.
1. Gantikan semua pemalar aditif dalam masa larian dengan pemalar 1.
2 Dalam fungsi masa berjalan yang diubah suai, hanya istilah tertib tertinggi dikekalkan.
3 Jika sebutan tertib tertinggi wujud dan bukan 1, keluarkan pemalar yang didarab dengan sebutan ini. Hasilnya ialah pesanan Big O.

Melalui perkara di atas kita akan mendapati bahawa perwakilan asimptotik Big O mengalih keluar item yang mempunyai sedikit kesan ke atas keputusan, dan menyatakan bilangan pelaksanaan secara ringkas dan jelas.
Selain itu, terdapat senario terbaik, sederhana dan terburuk untuk kerumitan masa beberapa algoritma:
Senario terburuk: bilangan maksimum larian (batas atas) untuk sebarang input saiz
Purata kes: bilangan jangkaan larian untuk sebarang saiz input
Kes terbaik: bilangan minimum larian (batas bawah) untuk sebarang saiz input
Contohnya: mencari data x dalam tatasusunan panjang N
Kes terbaik: 1 kali ditemui
Kes terburuk: N kali ditemui
Purata kes: N/2 kali ditemui
Situasi umum dalam amalan Tumpuan adalah pada situasi operasi algoritma yang paling teruk, jadi kerumitan masa mencari data dalam tatasusunan ialah O(N)
Kerumitan masa pengiraan
Contoh 1:

Operasi asas dilakukan 2N+10 kali dengan memperoleh kaedah O-order yang besar, kita tahu bahawa kerumitan masa ialah O(N)
Contoh 2:
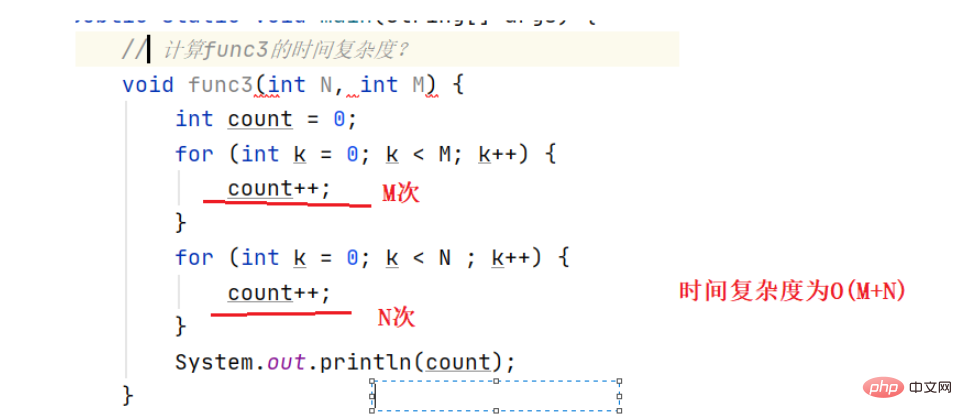
Operasi asas dilakukan M+N kali, terdapat dua M dan N yang tidak diketahui, dan kerumitan masa ialah O(N+ M)
Contoh 3:

Operasi asas dilakukan sebanyak 100 kali Dengan memperoleh kaedah tertib-O besar, kerumitan masa ialah O(1 )
Contoh 4: Mengira kerumitan masa bagi jenis gelembung

Operasi asas dilaksanakan N kali terbaik, dan (N*(N-1 ))/2 kali paling teruk Dengan memperoleh kaedah tertib O yang besar + kerumitan masa, yang paling teruk biasanya dilihat , kerumitan masa ialah O(N^2
Contoh 5: Kerumitan masa carian binari

Operasi asas dilakukan sekali pada masa terbaik, dan pada masa paling teruk O(logN), kerumitan masa ialah O(logN) ps: Dalam analisis algoritma, logN bermaksud bahawa asas ialah 2 dan logaritma ialah N. Di sesetengah tempat, ia ditulis sebagai lgN (disyorkan untuk menerangkan cara logN dikira melalui carian origami. out) (Oleh kerana carian binari menghapuskan separuh daripada nilai yang tidak sesuai setiap kali, baki nilai selepas satu carian binari ialah: n/2, dan baki nilai selepas dua carian binari ialah: n/2/2 = n/4)
Contoh soalan 6: Kira kerumitan masa rekursi faktorial
Kerumitan masa rekursi = bilangan ulangan * bilangan kali setiap ulangan dilaksanakan

Temui operasi asas melalui pengiraan dan analisis Diulang N kali, kerumitan masa ialah O(N)
Contoh 7: Kira kerumitan masa rekursi Fibonacci

Melalui pengiraan dan analisis, didapati operasi asas adalah rekursif 2^N kali, dan kerumitan masa ialah O(2^N).
Peraturan:
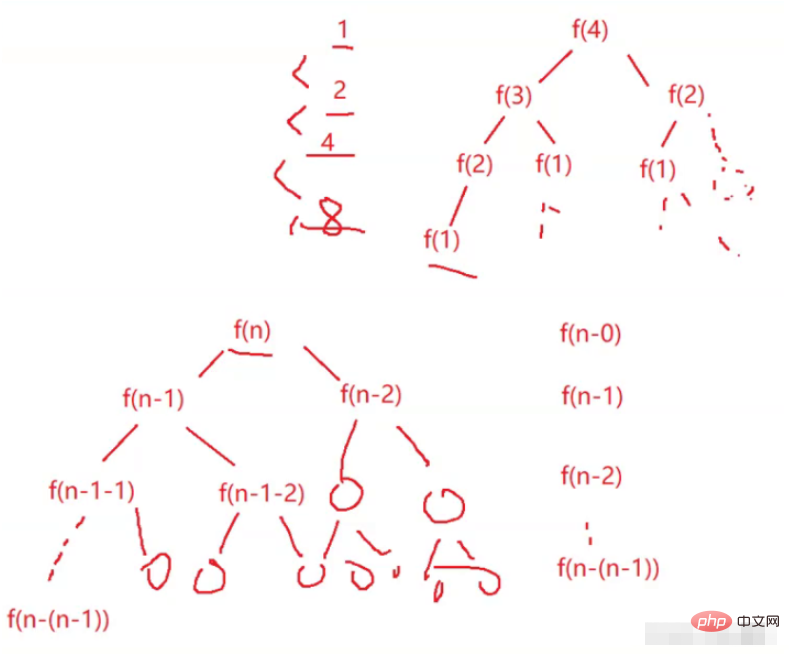
2^0+2^1+2^2+2^3……2^(n-(n-1) ))
Jumlah jujukan geometri
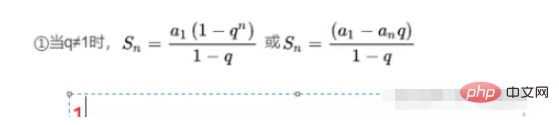
a1 mewakili sebutan pertama, q ialah geometri, iaitu 2, 1(1-2^n) / -1, bersamaan dengan 2^n+1, jadi kerumitan masa ialah O(2^n)
3. Kerumitan ruang
Kerumitan ruang ialah pengukuran proses berjalan sesuatu algoritma Ukuran jumlah ruang penyimpanan yang diduduki buat sementara waktu. Kerumitan ruang bukanlah berapa banyak bait ruang yang diduduki oleh program, kerana ini tidak begitu bermakna, jadi kerumitan ruang dikira dengan bilangan pembolehubah. Peraturan pengiraan kerumitan ruang pada asasnya serupa dengan kerumitan praktikal, dan notasi asimptotik O besar juga digunakan.
Contoh 1: Mengira kerumitan ruang jenis gelembung
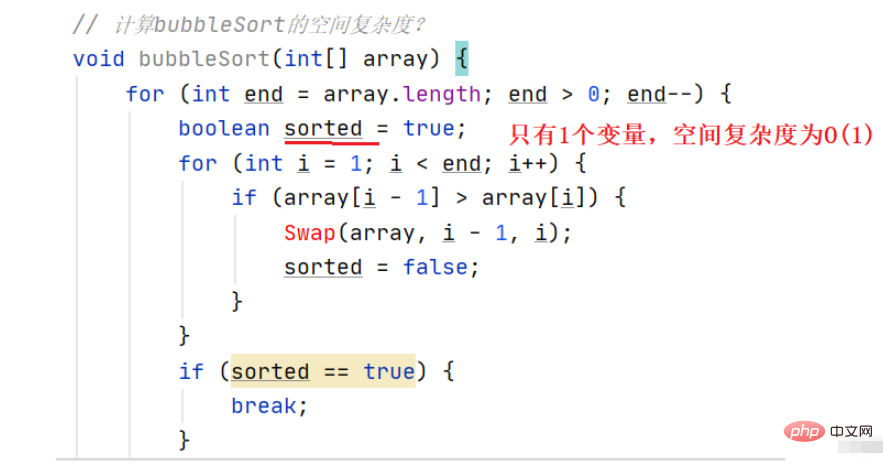
menggunakan ruang tambahan yang berterusan, jadi kerumitan ruang ialah O(1)
Contoh 2: Kira kerumitan ruang Fibonacci
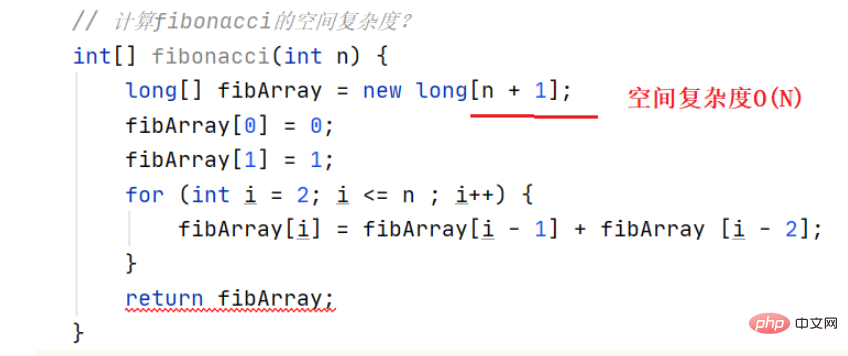
Membuka N ruang secara dinamik dan kerumitan ruang ialah O(N)
Contoh 3: Kira kerumitan ruang bagi rekursi faktorial

Rekursi dipanggil N kali, N bingkai tindanan dibuka dan setiap bingkai tindanan menggunakan jumlah ruang yang tetap. Kerumitan ruang ialah O(N)
Atas ialah kandungan terperinci Kerumitan masa Java dan analisis contoh kerumitan ruang. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1382
1382
 52
52
 Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan Nombor Sempurna di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor Perfect dalam Java?, contoh dengan pelaksanaan kod.
 Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Weka di Jawa. Di sini kita membincangkan Pengenalan, cara menggunakan weka java, jenis platform, dan kelebihan dengan contoh.
 Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Nombor Smith di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor smith di Jawa? contoh dengan pelaksanaan kod.
 Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Dalam artikel ini, kami telah menyimpan Soalan Temuduga Spring Java yang paling banyak ditanya dengan jawapan terperinci mereka. Supaya anda boleh memecahkan temuduga.
 Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Java 8 memperkenalkan API Stream, menyediakan cara yang kuat dan ekspresif untuk memproses koleksi data. Walau bagaimanapun, soalan biasa apabila menggunakan aliran adalah: bagaimana untuk memecahkan atau kembali dari operasi foreach? Gelung tradisional membolehkan gangguan awal atau pulangan, tetapi kaedah Foreach Stream tidak menyokong secara langsung kaedah ini. Artikel ini akan menerangkan sebab -sebab dan meneroka kaedah alternatif untuk melaksanakan penamatan pramatang dalam sistem pemprosesan aliran. Bacaan Lanjut: Penambahbaikan API Java Stream Memahami aliran aliran Kaedah Foreach adalah operasi terminal yang melakukan satu operasi pada setiap elemen dalam aliran. Niat reka bentuknya adalah
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Panduan untuk TimeStamp to Date di Java. Di sini kita juga membincangkan pengenalan dan cara menukar cap waktu kepada tarikh dalam java bersama-sama dengan contoh.
 Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Kapsul adalah angka geometri tiga dimensi, terdiri daripada silinder dan hemisfera di kedua-dua hujungnya. Jumlah kapsul boleh dikira dengan menambahkan isipadu silinder dan jumlah hemisfera di kedua -dua hujungnya. Tutorial ini akan membincangkan cara mengira jumlah kapsul yang diberikan dalam Java menggunakan kaedah yang berbeza. Formula volum kapsul Formula untuk jumlah kapsul adalah seperti berikut: Kelantangan kapsul = isipadu isipadu silinder Dua jumlah hemisfera dalam, R: Radius hemisfera. H: Ketinggian silinder (tidak termasuk hemisfera). Contoh 1 masukkan Jejari = 5 unit Ketinggian = 10 unit Output Jilid = 1570.8 Unit padu menjelaskan Kirakan kelantangan menggunakan formula: Kelantangan = π × r2 × h (4
 Bagaimana untuk menjalankan aplikasi boot musim bunga pertama anda di Spring Tool Suite?
Feb 07, 2025 pm 12:11 PM
Bagaimana untuk menjalankan aplikasi boot musim bunga pertama anda di Spring Tool Suite?
Feb 07, 2025 pm 12:11 PM
Spring Boot memudahkan penciptaan aplikasi Java yang mantap, berskala, dan siap pengeluaran, merevolusi pembangunan Java. Pendekatan "Konvensyen Lebih Konfigurasi", yang wujud pada ekosistem musim bunga, meminimumkan persediaan manual, Allo




