 Peranti teknologi
Peranti teknologi
 AI
AI
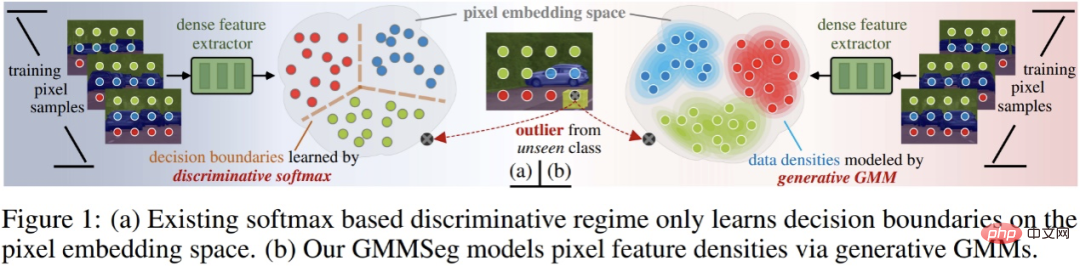
 GMMSeg, paradigma baharu segmentasi semantik generatif, boleh mengendalikan pengecaman set tertutup dan set terbuka
GMMSeg, paradigma baharu segmentasi semantik generatif, boleh mengendalikan pengecaman set tertutup dan set terbuka
GMMSeg, paradigma baharu segmentasi semantik generatif, boleh mengendalikan pengecaman set tertutup dan set terbuka
Algoritma segmentasi semantik arus perdana pada asasnya ialah model pengelasan diskriminatif berdasarkan pengelas softmax, yang secara langsung memodelkan p (kelas|ciri piksel) dan mengabaikan sepenuhnya pengedaran data piksel asas, iaitu, p ( kelas| ciri piksel). Ini mengehadkan ekspresi dan generalisasi model pada data OOD (luar pengedaran).
Dalam kajian baru-baru ini, penyelidik dari Universiti Zhejiang, Universiti Teknologi Sydney dan Institut Penyelidikan Baidu mencadangkan paradigma pembahagian semantik baharu - berdasarkan model pembahagian semantik generatif Gaussian mixture (GMM) GMMSeg.

- Pautan kertas: https://arxiv.org/abs/2210.02025
- Pautan kod: https://github.com/leonnnop/GMMSeg
GMMSeg melaksanakan pengedaran bersama piksel dan kategori Pemodelan menggunakan algoritma EM untuk mempelajari pengelas campuran Gaussian (GMM Classifier) dalam ruang ciri piksel, dan menggunakan paradigma generatif untuk menangkap secara halus taburan ciri piksel bagi setiap kategori. Sementara itu, GMMSeg menggunakan kehilangan diskriminasi untuk mengoptimumkan pengekstrak ciri mendalam dari hujung ke hujung. Ini memberikan GMMSeg kelebihan kedua-dua model diskriminatif dan generatif.
Hasil eksperimen menunjukkan bahawa GMMSeg telah mencapai peningkatan prestasi pada pelbagai seni bina segmentasi dan rangkaian tulang belakang pada masa yang sama, tanpa sebarang pasca pemprosesan atau penalaan halus, GMMSeg boleh secara langsung digunakan untuk tugas pembahagian anomali.
Sehingga kini, ini adalah kali pertama kaedah pembahagian semantik boleh menggunakan contoh model tunggal, dalam kedua-dua set tertutup dan set terbuka serentak mencapai prestasi lanjutan dalam keadaan dunia terbuka. Ini juga merupakan kali pertama pengelas generatif menunjukkan kelebihan dalam tugas penglihatan berskala besar.
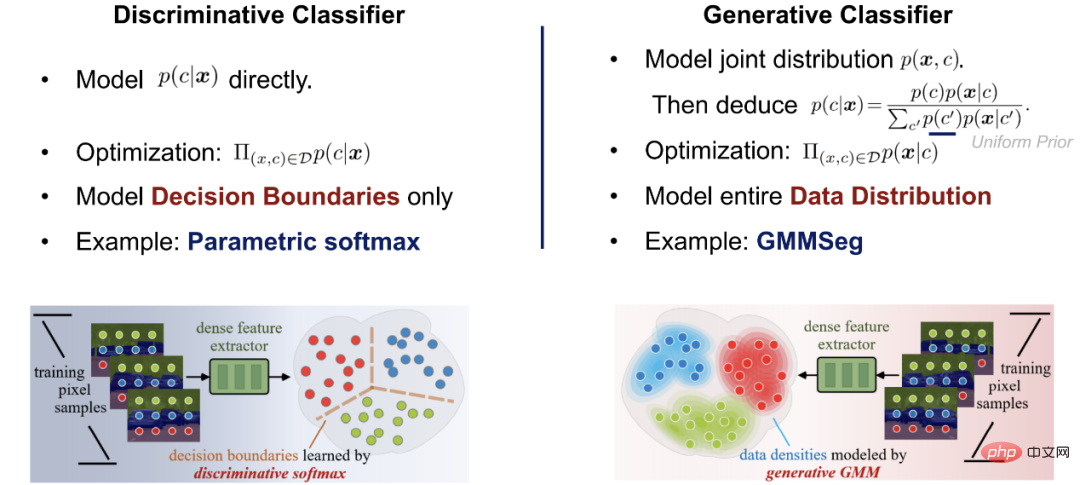
Diskriminan vs. Pengelas Generatif
Sebelum mendalami paradigma segmentasi sedia ada dan kaedah yang dicadangkan, pengenalan ringkas disediakan di sini. konsep pengelas diskriminatif dan generatif.
Andaikan terdapat set data D, yang mengandungi pasangan sampel - pasangan label (x, y); kebarangkalian pengelasan sampel p (y|x). Kaedah pengelasan boleh dibahagikan kepada dua kategori: pengelas diskriminatif dan pengelas generatif.
- Pengelas diskriminasi: secara langsung memodelkan kebarangkalian bersyarat p (y|x); ia hanya mempelajari sempadan keputusan yang optimum untuk pengelasan, dan sepenuhnya Ia melakukannya tidak mempertimbangkan pengedaran sampel itu sendiri dan oleh itu tidak dapat mencerminkan ciri-ciri sampel.
- Pengelas generatif: model pertama taburan kebarangkalian bersama p (x, y), dan kemudian terbitkan kebarangkalian bersyarat pengelasan melalui teorem Bayes yang jelas kepada modelnya pengedaran data itu sendiri, model yang sepadan sering diwujudkan untuk setiap kategori. Berbanding dengan pengelas diskriminatif, ia mempertimbangkan sepenuhnya maklumat ciri sampel.
Paradigma pembahagian semantik arus perdana: pengelas Softmax diskriminatif
Kebanyakan model pembahagian piksel demi piksel arus perdana semasa gunakan kedalaman Rangkaian mengekstrak ciri piksel, dan kemudian menggunakan pengelas softmax untuk mengelaskan ciri piksel. Seni bina rangkaiannya terdiri daripada dua bahagian:
Bahagian pertama ialah pengekstrak ciri piksel dan seni bina tipikalnya ialah penyahkod pengekod pasangan , ciri piksel diperoleh dengan memetakan input piksel ruang RGB ke ruang dimensi tinggi D-dimensi.
Bahagian kedua ialah pengelas piksel, iaitu pengelas softmax arus perdana; ia mengekodkan ciri piksel input ke dalam kelas C Real output nombor (logits), dan kemudian gunakan fungsi softmax untuk menormalkan output (logit) dan tetapkan makna kebarangkalian, iaitu, gunakan logit untuk mengira kebarangkalian posterior klasifikasi piksel:
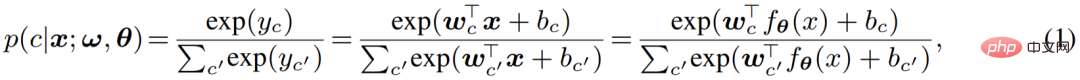
Akhir sekali, model lengkap yang terdiri daripada dua bahagian akan dioptimumkan hujung ke hujung melalui kehilangan entropi silang:
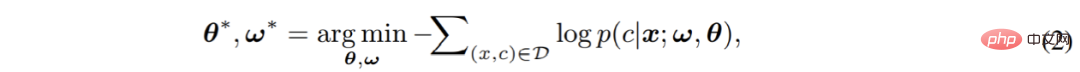
Di sini Dalam proses, model mengabaikan taburan piksel itu sendiri dan menganggarkan secara langsung kebarangkalian bersyarat p (c|x) ramalan pengelasan piksel. Dapat dilihat bahawa pengelas softmax arus perdana pada dasarnya adalah pengelas diskriminatif . Pengelas diskriminasi mempunyai struktur yang ringkas dan kerana matlamat pengoptimumannya secara langsung bertujuan untuk mengurangkan ralat diskriminasi, ia selalunya boleh mencapai prestasi diskriminasi yang sangat baik. Walau bagaimanapun, pada masa yang sama, ia mempunyai beberapa kekurangan maut yang tidak menarik perhatian kerja sedia ada, yang sangat mempengaruhi prestasi klasifikasi dan generalisasi pengelas softmax:
Pertama sekali , yang hanya memodelkan sempadan keputusan sepenuhnya mengabaikan pengedaran ciri piksel, dan oleh itu tidak boleh memodelkan dan menggunakan ciri khusus setiap kategori melemahkan keupayaan generalisasi dan ekspresinya;
- Kedua, ia menggunakan pasangan parameter tunggal ( w
- ,b) untuk memodelkan kelas dengan kata lain, pengelas softmax bergantung pada andaian unimodaliti ini andaian yang sangat kuat dan terlalu dipermudahkan sering gagal untuk digunakan dalam aplikasi praktikal, menyebabkan hanya prestasi yang tidak optimum. Akhir sekali, output pengelas softmax tidak dapat menggambarkan dengan tepat maksud kebarangkalian sebenar ramalan terakhirnya hanya boleh digunakan sebagai rujukan apabila membandingkan dengan kategori lain. Ini juga merupakan sebab asas mengapa sebilangan besar model pembahagian arus perdana sukar untuk mengesan input OOD.
- Sebagai tindak balas kepada masalah ini, penulis percaya bahawa paradigma diskriminatif arus perdana perlu difikirkan semula, dan penyelesaian yang sepadan diberikan dalam artikel ini: Model Segmentasi Semantik Generatif— — GMMSeg.
Model segmentasi semantik generatif: GMMSeg
Pengarang menyusun semula proses segmentasi semantik dari perspektif model generatif. Berbanding dengan memodelkan secara langsung kebarangkalian pengelasan p (c|
x), pengelas generatif memodelkan taburan bersama p (x, c) dan kemudian menggunakan teorem Bayes Terbitkan kebarangkalian pengelasan:
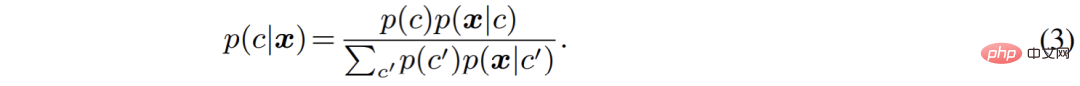 Antaranya, untuk pertimbangan generalisasi, kategori sebelum p (c) selalunya ditetapkan kepada pengedaran seragam, dan Bagaimana untuk memodelkan kategori bersyarat pengedaran p (
Antaranya, untuk pertimbangan generalisasi, kategori sebelum p (c) selalunya ditetapkan kepada pengedaran seragam, dan Bagaimana untuk memodelkan kategori bersyarat pengedaran p (
|c) ciri piksel telah menjadi isu utama pada masa ini. Dalam kertas ini, iaitu GMMSeg, model campuran Gaussian digunakan untuk memodelkan p (
x|c), yang mempunyai bentuk berikut:
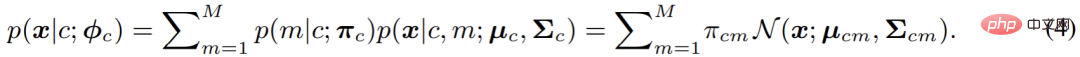 Apabila bilangan komponen tidak terhad, model campuran Gaussian secara teorinya boleh memuatkan sebarang pengedaran, jadi ia sangat elegan dan berkuasa pada masa yang sama, The sifat model hibridnya juga menjadikannya layak untuk memodelkan pelbagai mod, iaitu, untuk memodelkan variasi dalam kelas. Berdasarkan ini, artikel ini menggunakan anggaran kemungkinan maksimum untuk mengoptimumkan parameter model:
Apabila bilangan komponen tidak terhad, model campuran Gaussian secara teorinya boleh memuatkan sebarang pengedaran, jadi ia sangat elegan dan berkuasa pada masa yang sama, The sifat model hibridnya juga menjadikannya layak untuk memodelkan pelbagai mod, iaitu, untuk memodelkan variasi dalam kelas. Berdasarkan ini, artikel ini menggunakan anggaran kemungkinan maksimum untuk mengoptimumkan parameter model:
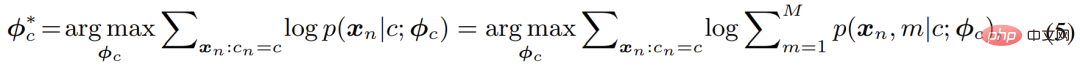 Penyelesaian klasik ialah algoritma EM, iaitu, dengan melaksanakan secara bergilir-gilir E-M - Pengoptimuman dua langkah demi langkah bagi F - fungsi:
Penyelesaian klasik ialah algoritma EM, iaitu, dengan melaksanakan secara bergilir-gilir E-M - Pengoptimuman dua langkah demi langkah bagi F - fungsi:
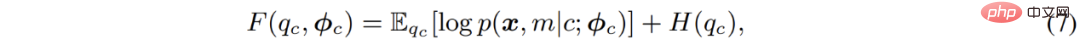
Khusus untuk pengoptimuman model campuran Gaussian, algoritma EM sebenarnya menganggarkan semula kebarangkalian bahawa titik data tergolong dalam setiap submodel dalam E-step. Dalam erti kata lain, ia adalah bersamaan dengan pengelompokan lembut piksel dalam langkah-E kemudian, dalam langkah-M, hasil pengelompokan boleh digunakan untuk mengemas kini parameter model sekali lagi.
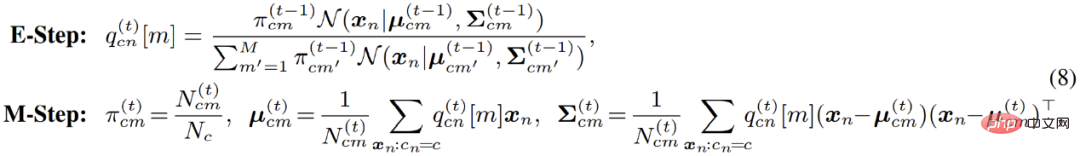
Walau bagaimanapun, dalam aplikasi praktikal, penulis mendapati bahawa algoritma EM standard menumpu secara perlahan dan keputusan akhir adalah lemah. Penulis mengesyaki bahawa algoritma EM terlalu sensitif kepada nilai awal pengoptimuman parameter, menjadikannya sukar untuk menumpu ke titik ekstrem tempatan yang lebih baik. Diilhamkan oleh satu siri algoritma pengelompokan terkini berdasarkan teori pengangkutan optimum, penulis memperkenalkan seragam tambahan sebelum pengedaran model campuran:
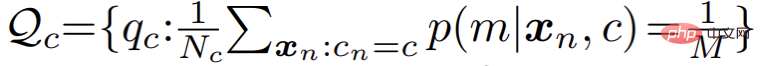
Sejajar dengan itu, E-langkah dalam proses pengoptimuman parameter diubah menjadi masalah pengoptimuman yang terhad, seperti berikut:
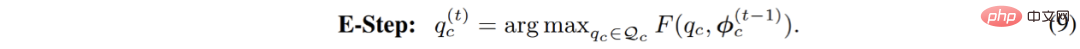
Proses ini boleh difahami secara intuitif, sama kekangan pengedaran diperkenalkan kepada proses pengelompokan: semasa proses pengelompokan, titik data boleh diagihkan secara sama rata kepada setiap sub-model pada tahap tertentu. Selepas memperkenalkan kekangan ini, proses pengoptimuman ini adalah bersamaan dengan masalah penghantaran optimum yang disenaraikan dalam formula berikut:
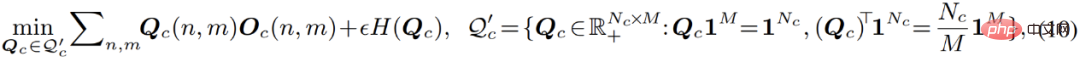
Formula ini boleh menggunakan Sinkhorn-Knopp The algoritma menyelesaikan dengan cepat. Keseluruhan proses pengoptimuman yang dipertingkatkan dinamakan Sinkhorn EM, yang telah dibuktikan oleh beberapa kerja teori untuk mempunyai penyelesaian optimum global yang sama seperti algoritma EM standard, dan kurang berkemungkinan jatuh ke dalam penyelesaian optimum tempatan.
Pengoptimuman Hibrid Dalam Talian
Selepas itu, dalam proses pengoptimuman lengkap, artikel menggunakan mod pengoptimuman hibrid dalam talian: Melalui Sinkhorn EM generatif, pengelas campuran Gaussian adalah dioptimumkan secara berterusan dalam ruang ciri yang dikemas kini secara beransur-ansur, manakala untuk bahagian lain daripada rangka kerja yang lengkap, bahagian pengekstrak ciri piksel, berdasarkan hasil ramalan pengelas generatif, gunakan Optimize dengan kehilangan rentas entropi yang diskriminatif. Kedua-dua bahagian dioptimumkan secara bergilir-gilir dan diselaraskan antara satu sama lain, menjadikan keseluruhan model diganding rapat dan berkeupayaan untuk latihan hujung ke hujung:

Dalam proses ini, ciri Bahagian pengekstrakan hanya dioptimumkan melalui perambatan belakang kecerunan manakala bahagian pengelas generatif hanya dioptimumkan melalui SinkhornEM. Reka bentuk pengoptimuman berselang-seli inilah yang membolehkan keseluruhan model disepadukan secara padat dan mewarisi kelebihan daripada model diskriminatif dan generatif.

Akhir sekali, GMMSeg mendapat manfaat daripada seni bina klasifikasi generatif dan strategi latihan hibrid dalam talian, menunjukkan ciri-ciri yang pengelas softmax yang diskriminatif tidak mempunyai Kelebihan:
- Pertama, mendapat manfaat daripada seni bina universalnya, GMMSeg serasi dengan kebanyakan model segmentasi arus perdana, iaitu, serasi dengan model yang menggunakan softmax untuk pengelasan: anda hanya perlu menggantikan pengelas softmax yang diskriminatif tanpa rasa sakit prestasi model sedia ada.
- Kedua, disebabkan penggunaan mod latihan hibrid, GMMSeg menggabungkan kelebihan pengelas generatif dan diskriminatif, dan pada tahap tertentu menyelesaikan masalah yang softmax tidak dapat memodelkan perubahan dalam kelas. ; sangat meningkatkan prestasi diskriminasinya.
- Ketiga, GMMSeg secara eksplisit memodelkan pengedaran ciri piksel, iaitu, p (x|c secara langsung boleh memberikan pengedaran sampel milik setiap satu); kategori Kebarangkalian, yang membolehkannya mengendalikan data OOD yang tidak kelihatan secara semula jadi.
Hasil eksperimen
Hasil percubaan menunjukkan bahawa sama ada ia berdasarkan seni bina CNN atau seni bina Transformer, dalam set data segmentasi semantik yang digunakan secara meluas (ADE20K, Cityscapes , COCO-Stuff), GMMSeg boleh mencapai peningkatan prestasi yang stabil dan jelas.
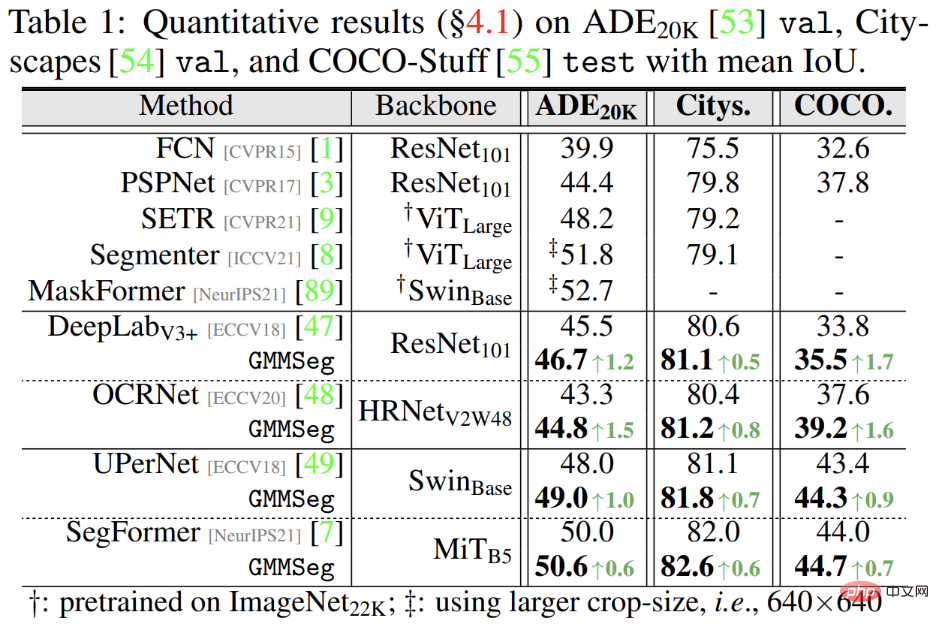

Selain itu, dalam tugasan segmentasi abnormal, tidak perlu berurusan dengan tugasan set tertutup , iaitu, biasa Jika sebarang pengubahsuaian dibuat kepada model terlatih dalam tugas pembahagian semantik, GMMSeg boleh mengatasi kaedah lain yang memerlukan pasca pemprosesan khas dalam semua penunjuk penilaian biasa.
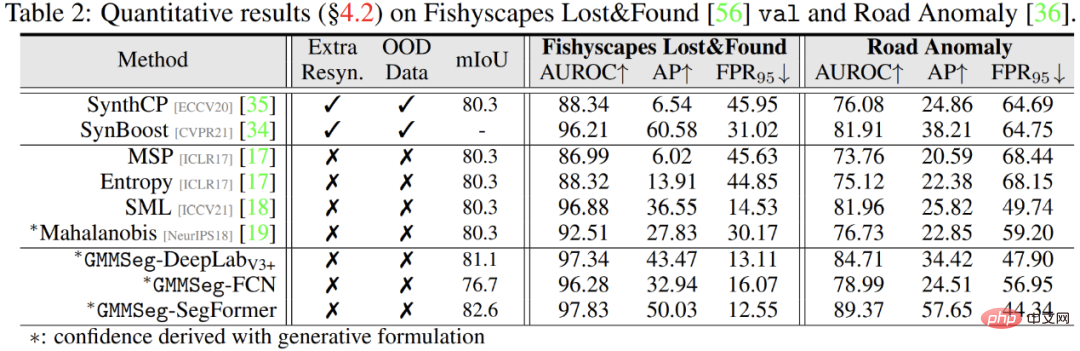

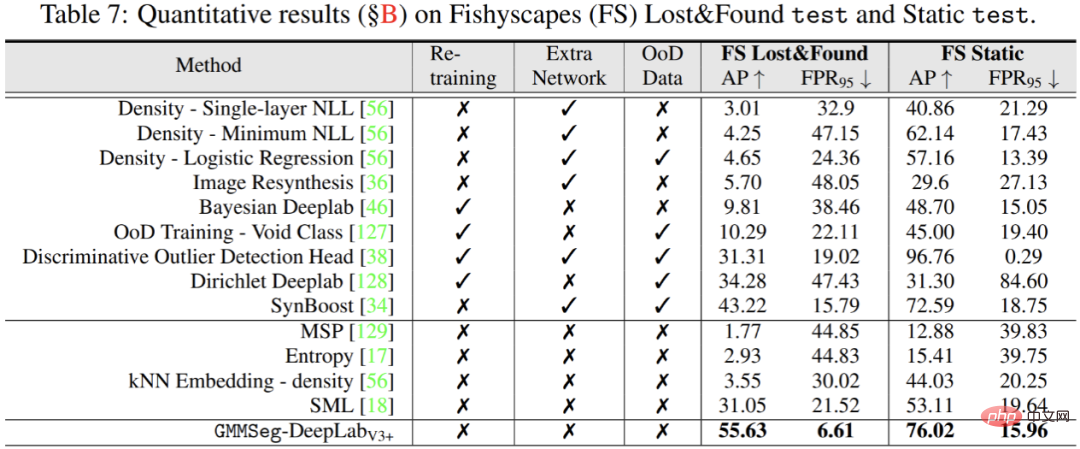
Atas ialah kandungan terperinci GMMSeg, paradigma baharu segmentasi semantik generatif, boleh mengendalikan pengecaman set tertutup dan set terbuka. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Model MoE sumber terbuka paling berkuasa di dunia ada di sini, dengan keupayaan bahasa Cina setanding dengan GPT-4, dan harganya hanya hampir satu peratus daripada GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Model MoE sumber terbuka paling berkuasa di dunia ada di sini, dengan keupayaan bahasa Cina setanding dengan GPT-4, dan harganya hanya hampir satu peratus daripada GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Bayangkan model kecerdasan buatan yang bukan sahaja mempunyai keupayaan untuk mengatasi pengkomputeran tradisional, tetapi juga mencapai prestasi yang lebih cekap pada kos yang lebih rendah. Ini bukan fiksyen sains, DeepSeek-V2[1], model MoE sumber terbuka paling berkuasa di dunia ada di sini. DeepSeek-V2 ialah gabungan model bahasa pakar (MoE) yang berkuasa dengan ciri-ciri latihan ekonomi dan inferens yang cekap. Ia terdiri daripada 236B parameter, 21B daripadanya digunakan untuk mengaktifkan setiap penanda. Berbanding dengan DeepSeek67B, DeepSeek-V2 mempunyai prestasi yang lebih kukuh, sambil menjimatkan 42.5% kos latihan, mengurangkan cache KV sebanyak 93.3% dan meningkatkan daya pemprosesan penjanaan maksimum kepada 5.76 kali. DeepSeek ialah sebuah syarikat yang meneroka kecerdasan buatan am
 Apr 09, 2024 am 11:52 AM
Apr 09, 2024 am 11:52 AM
AI memang mengubah matematik. Baru-baru ini, Tao Zhexuan, yang telah mengambil perhatian terhadap isu ini, telah memajukan keluaran terbaru "Buletin Persatuan Matematik Amerika" (Buletin Persatuan Matematik Amerika). Memfokuskan pada topik "Adakah mesin akan mengubah matematik?", ramai ahli matematik menyatakan pendapat mereka Seluruh proses itu penuh dengan percikan api, tegar dan menarik. Penulis mempunyai barisan yang kuat, termasuk pemenang Fields Medal Akshay Venkatesh, ahli matematik China Zheng Lejun, saintis komputer NYU Ernest Davis dan ramai lagi sarjana terkenal dalam industri. Dunia AI telah berubah secara mendadak Anda tahu, banyak artikel ini telah dihantar setahun yang lalu.
 Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas secara rasmi memasuki era robot elektrik! Semalam, Atlas hidraulik hanya "menangis" menarik diri daripada peringkat sejarah Hari ini, Boston Dynamics mengumumkan bahawa Atlas elektrik sedang berfungsi. Nampaknya dalam bidang robot humanoid komersial, Boston Dynamics berazam untuk bersaing dengan Tesla. Selepas video baharu itu dikeluarkan, ia telah pun ditonton oleh lebih sejuta orang dalam masa sepuluh jam sahaja. Orang lama pergi dan peranan baru muncul. Ini adalah keperluan sejarah. Tidak dinafikan bahawa tahun ini adalah tahun letupan robot humanoid. Netizen mengulas: Kemajuan robot telah menjadikan majlis pembukaan tahun ini kelihatan seperti manusia, dan tahap kebebasan adalah jauh lebih besar daripada manusia Tetapi adakah ini benar-benar bukan filem seram? Pada permulaan video, Atlas berbaring dengan tenang di atas tanah, seolah-olah terlentang. Apa yang berikut adalah rahang-jatuh
 KAN, yang menggantikan MLP, telah diperluaskan kepada konvolusi oleh projek sumber terbuka
Jun 01, 2024 pm 10:03 PM
KAN, yang menggantikan MLP, telah diperluaskan kepada konvolusi oleh projek sumber terbuka
Jun 01, 2024 pm 10:03 PM
Awal bulan ini, penyelidik dari MIT dan institusi lain mencadangkan alternatif yang sangat menjanjikan kepada MLP - KAN. KAN mengatasi MLP dari segi ketepatan dan kebolehtafsiran. Dan ia boleh mengatasi prestasi MLP berjalan dengan bilangan parameter yang lebih besar dengan bilangan parameter yang sangat kecil. Sebagai contoh, penulis menyatakan bahawa mereka menggunakan KAN untuk menghasilkan semula keputusan DeepMind dengan rangkaian yang lebih kecil dan tahap automasi yang lebih tinggi. Khususnya, MLP DeepMind mempunyai kira-kira 300,000 parameter, manakala KAN hanya mempunyai kira-kira 200 parameter. KAN mempunyai asas matematik yang kukuh seperti MLP berdasarkan teorem penghampiran universal, manakala KAN berdasarkan teorem perwakilan Kolmogorov-Arnold. Seperti yang ditunjukkan dalam rajah di bawah, KAN telah
 Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Prestasi JAX, yang dipromosikan oleh Google, telah mengatasi Pytorch dan TensorFlow dalam ujian penanda aras baru-baru ini, menduduki tempat pertama dalam 7 penunjuk. Dan ujian tidak dilakukan pada TPU dengan prestasi JAX terbaik. Walaupun dalam kalangan pembangun, Pytorch masih lebih popular daripada Tensorflow. Tetapi pada masa hadapan, mungkin lebih banyak model besar akan dilatih dan dijalankan berdasarkan platform JAX. Model Baru-baru ini, pasukan Keras menanda aras tiga hujung belakang (TensorFlow, JAX, PyTorch) dengan pelaksanaan PyTorch asli dan Keras2 dengan TensorFlow. Pertama, mereka memilih satu set arus perdana
 Kerja baharu pada ramalan siri masa + model besar NLP: secara automatik menjana gesaan tersirat untuk ramalan siri masa
Mar 18, 2024 am 09:20 AM
Kerja baharu pada ramalan siri masa + model besar NLP: secara automatik menjana gesaan tersirat untuk ramalan siri masa
Mar 18, 2024 am 09:20 AM
Hari ini saya ingin berkongsi kerja penyelidikan terbaru dari University of Connecticut yang mencadangkan kaedah untuk menyelaraskan data siri masa dengan model pemprosesan bahasa semula jadi (NLP) yang besar pada ruang terpendam untuk meningkatkan prestasi peramalan siri masa. Kunci kepada kaedah ini ialah menggunakan petunjuk spatial terpendam (prompt) untuk meningkatkan ketepatan ramalan siri masa. Tajuk kertas: S2IP-LLM: SemanticSpaceInformedPromptLearningwithLLMforTimeSeriesForecasting Alamat muat turun: https://arxiv.org/pdf/2403.05798v1.pdf 1. Model latar belakang masalah besar
 Robot Tesla bekerja di kilang, Musk: Tahap kebebasan tangan akan mencapai 22 tahun ini!
May 06, 2024 pm 04:13 PM
Robot Tesla bekerja di kilang, Musk: Tahap kebebasan tangan akan mencapai 22 tahun ini!
May 06, 2024 pm 04:13 PM
Video terbaru robot Tesla Optimus dikeluarkan, dan ia sudah boleh berfungsi di kilang. Pada kelajuan biasa, ia mengisih bateri (bateri 4680 Tesla) seperti ini: Pegawai itu juga mengeluarkan rupanya pada kelajuan 20x - pada "stesen kerja" kecil, memilih dan memilih dan memilih: Kali ini ia dikeluarkan Salah satu sorotan video itu ialah Optimus menyelesaikan kerja ini di kilang, sepenuhnya secara autonomi, tanpa campur tangan manusia sepanjang proses. Dan dari perspektif Optimus, ia juga boleh mengambil dan meletakkan bateri yang bengkok, memfokuskan pada pembetulan ralat automatik: Berkenaan tangan Optimus, saintis NVIDIA Jim Fan memberikan penilaian yang tinggi: Tangan Optimus adalah robot lima jari di dunia paling cerdik. Tangannya bukan sahaja boleh disentuh
 FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
Pengesanan objek ialah masalah yang agak matang dalam sistem pemanduan autonomi, antaranya pengesanan pejalan kaki adalah salah satu algoritma terawal untuk digunakan. Penyelidikan yang sangat komprehensif telah dijalankan dalam kebanyakan kertas kerja. Walau bagaimanapun, persepsi jarak menggunakan kamera fisheye untuk pandangan sekeliling agak kurang dikaji. Disebabkan herotan jejari yang besar, perwakilan kotak sempadan standard sukar dilaksanakan dalam kamera fisheye. Untuk mengurangkan perihalan di atas, kami meneroka kotak sempadan lanjutan, elips dan reka bentuk poligon am ke dalam perwakilan kutub/sudut dan mentakrifkan metrik mIOU pembahagian contoh untuk menganalisis perwakilan ini. Model fisheyeDetNet yang dicadangkan dengan bentuk poligon mengatasi model lain dan pada masa yang sama mencapai 49.5% mAP pada set data kamera fisheye Valeo untuk pemanduan autonomi



