 Peranti teknologi
Peranti teknologi
 AI
AI
 Ringkasan perbandingan lima model pembelajaran mendalam untuk ramalan siri masa
Ringkasan perbandingan lima model pembelajaran mendalam untuk ramalan siri masa
Ringkasan perbandingan lima model pembelajaran mendalam untuk ramalan siri masa
Siri Pertandingan M Makridakis (masing-masing dikenali sebagai M4 dan M5) telah diadakan pada tahun 2018 dan 2020 (M6 juga diadakan pada tahun ini). Bagi mereka yang tidak tahu, siri-m boleh dianggap sebagai ringkasan keadaan semasa ekosistem siri masa, memberikan bukti empirikal dan objektif untuk teori dan amalan ramalan semasa.
Keputusan M4 2018 menunjukkan bahawa kaedah "ML" tulen mengatasi kaedah statistik tradisional secara besar-besaran, yang tidak dijangka pada masa itu. Dalam M5[1] dua tahun kemudian, skor tertinggi adalah dengan hanya kaedah "ML". Dan semua 50 teratas pada asasnya berdasarkan ML (kebanyakannya model pokok). Pertandingan ini menyaksikan debut LightGBM (untuk ramalan siri masa) serta Deepar [2] dan N-Beats [3] Amazon. Model N-Beats dikeluarkan pada tahun 2020 dan 3% lebih baik daripada pemenang pertandingan M4!
Pertandingan Ramalan Tekanan Ventilator baru-baru ini menunjukkan kepentingan menggunakan kaedah pembelajaran mendalam untuk menangani cabaran siri masa masa nyata. Matlamat pertandingan adalah untuk meramalkan urutan temporal tekanan dalam paru-paru mekanikal. Setiap contoh latihan ialah siri masanya sendiri, jadi tugas itu adalah masalah siri masa berbilang. Pasukan pemenang menyerahkan seni bina dalam berbilang lapisan yang termasuk rangkaian LSTM dan blok Transformer.
Dalam beberapa tahun kebelakangan ini, banyak seni bina terkenal telah dikeluarkan, seperti MQRNN dan DSSM. Kesemua model ini menyumbang banyak perkara baharu kepada bidang peramalan siri masa menggunakan pembelajaran mendalam. Selain memenangi pertandingan Kaggle, ia juga membawa kami lebih banyak kemajuan seperti:
- Kepelbagaian: keupayaan untuk menggunakan model untuk tugasan yang berbeza.
- MLOP: Keupayaan untuk menggunakan model dalam pengeluaran.
- Kebolehtafsiran dan Kebolehtafsiran: Model kotak hitam tidak begitu popular.
Artikel ini membincangkan 5 seni bina pembelajaran mendalam yang pakar dalam ramalan siri masa ialah:
- N-BEATS (ElementAI)
- DeepAR (. Amazon)
- Spacetimeformer[4]
- Temporal Fusion Transformer atau TFT (Google) [5]
- TSFormer (MAE dalam siri masa)[7]
N-BEATS
Model ini datang terus daripada (malangnya) syarikat ElementAI yang berumur pendek, yang diasaskan bersama oleh Yoshua Bengio. Seni bina peringkat atas dan komponen utamanya ditunjukkan dalam Rajah 1:
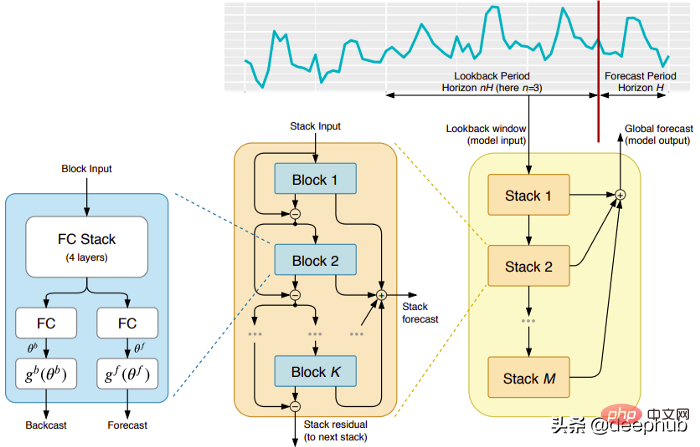
N-BEATS ialah seni bina pembelajaran mendalam tulen berdasarkan susunan mendalam rangkaian suapan hadapan bersepadu . Penimbunan juga dilakukan melalui sambungan ke hadapan dan belakang.
Setiap blok hanya memodelkan baki ralat yang dihasilkan oleh siaran belakang sebelumnya, dan kemudian mengemas kini ramalan berdasarkan ralat ini. Proses ini mensimulasikan kaedah Box-Jenkins apabila memasang model ARIMA.
Berikut ialah kelebihan utama model ini:
Ekspresif dan mudah digunakan: Model ini mudah difahami, mempunyai struktur modular, ia direka bentuk untuk memerlukan kejuruteraan ciri siri masa yang minimum dan tidak memerlukan Input perlu diskalakan.
Model ini mempunyai keupayaan untuk membuat generalisasi merentas berbilang siri masa. Dalam erti kata lain, siri masa yang berbeza dengan pengagihan yang sedikit berbeza boleh digunakan sebagai input. Dalam N-BEATS, ia dilaksanakan melalui meta-pembelajaran. Proses meta-pembelajaran merangkumi dua proses: proses pembelajaran dalaman dan proses pembelajaran luaran. Proses pembelajaran dalaman berlaku di dalam blok dan membantu model menangkap ciri temporal tempatan. Proses pembelajaran luaran berlaku dalam susun lapis dan membantu model mempelajari ciri global bagi semua siri masa.
Penyusun baki berganda: Idea sambungan dan penyusunan sisa adalah sangat bijak, dan ia digunakan dalam hampir setiap jenis rangkaian saraf dalam. Prinsip yang sama digunakan dalam pelaksanaan N-BEATS, tetapi dengan beberapa pengubahsuaian tambahan: setiap blok mempunyai dua cawangan baki, satu berjalan dalam tetingkap lihat belakang (dipanggil backcast) dan satu lagi berjalan dalam tetingkap ramalan (dipanggil untuk ramalan).
Setiap blok berturut-turut hanya memodelkan baki yang terhasil daripada siaran belakang yang dibina semula bagi blok sebelumnya, dan kemudian mengemas kini ramalan berdasarkan ralat itu. Ini membantu model menganggarkan isyarat siaran belakang yang berguna dengan lebih baik, manakala ramalan ramalan tindanan akhir dimodelkan sebagai jumlah hierarki semua ramalan separa. Proses inilah yang mensimulasikan kaedah Box-Jenkins bagi model ARIMA.
Kebolehtafsiran: Model ini datang dalam dua varian, universal dan boleh ditafsir. Dalam varian umum, rangkaian secara sewenang-wenangnya mempelajari pemberat akhir bagi lapisan yang disambungkan sepenuhnya bagi setiap blok. Dalam varian yang boleh ditafsir, lapisan terakhir setiap blok dialih keluar. Cawangan backcast dan ramalan kemudiannya didarab dengan aliran simulasi matriks tertentu (fungsi monotonik) dan kemusim (fungsi kitaran kitaran).
Nota: Pelaksanaan N-BEATS asal hanya berfungsi dengan siri masa univariate.
DeepAR
Model siri masa novel yang menggabungkan pembelajaran mendalam dan ciri autoregresif. Rajah 2 menunjukkan seni bina peringkat atas DeepAR:
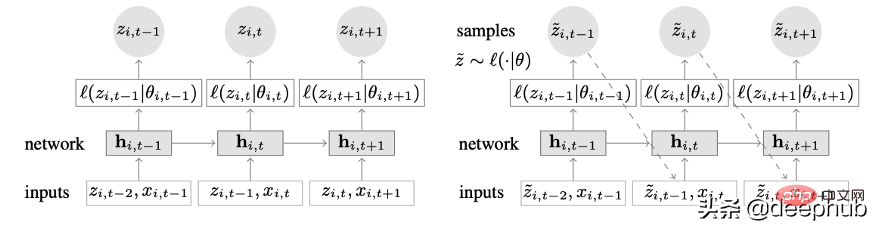
Berikut ialah kelebihan utama model ini:
DeepAR berfungsi dengan baik pada berbilang siri masa: dengan menggunakan berbilang siri masa dengan pengedaran yang sedikit berbeza . Juga boleh digunakan pada banyak senario kehidupan sebenar. Sebagai contoh, syarikat kuasa mungkin ingin melancarkan perkhidmatan ramalan kuasa untuk setiap pelanggan, setiap satunya mempunyai corak penggunaan yang berbeza (yang bermaksud pengagihan yang berbeza).
Selain data sejarah, DeepAR juga membenarkan penggunaan siri masa masa hadapan yang diketahui (ciri model autoregresif) dan atribut statik tambahan. Dalam senario ramalan permintaan elektrik yang dinyatakan sebelum ini, pembolehubah masa tambahan boleh menjadi bulan (sebagai integer dengan nilai antara 1-12). Dengan mengandaikan setiap pelanggan dikaitkan dengan penderia yang mengukur penggunaan kuasa, pembolehubah statik tambahan adalah seperti sensor_id atau customer_id.
Jika anda sudah biasa menggunakan seni bina rangkaian saraf seperti MLP dan RNN untuk ramalan siri masa, langkah prapemprosesan utama ialah menskalakan siri masa menggunakan teknik penormalan atau penormalan. Ini tidak memerlukan operasi manual dalam DeepAR, kerana model asas menskalakan input autoregresif z untuk setiap siri masa i dengan faktor penskalaan v_i, iaitu min bagi siri masa itu. Secara khusus, persamaan faktor skala yang digunakan dalam penanda aras kertas adalah seperti berikut:

Walau bagaimanapun, dalam praktiknya, jika saiz siri masa sasaran sangat berbeza, maka semasa prapemprosesan Ia masih perlu untuk menggunakan penskalaan anda sendiri. Contohnya, dalam senario ramalan permintaan tenaga, set data mungkin mengandungi pelanggan elektrik voltan sederhana (seperti kilang kecil, menggunakan elektrik dalam megawatt) dan pelanggan voltan rendah (seperti isi rumah, menggunakan elektrik dalam kilowatt).
DeepAR membuat ramalan kebarangkalian dan bukannya secara langsung mengeluarkan nilai masa hadapan. Ini dilakukan sebagai sampel Monte Carlo. Ramalan ini digunakan untuk mengira ramalan kuantil dengan menggunakan fungsi kehilangan kuantil. Bagi mereka yang tidak biasa dengan jenis kerugian ini, kerugian kuantiti digunakan untuk mengira bukan sahaja anggaran, tetapi selang ramalan sekitar nilai tersebut.
Spacetimeformer
Pergantungan masa adalah yang paling penting dalam siri masa univariate. Tetapi dalam beberapa senario siri masa, perkara tidak semudah itu. Sebagai contoh, katakan kita mempunyai tugas ramalan cuaca dan ingin meramalkan suhu lima bandar. Mari kita anggap bandar-bandar ini milik sesebuah negara. Memandangkan apa yang telah kita lihat setakat ini, kita boleh menggunakan DeepAR dan memodelkan setiap bandar sebagai kovariat statik luaran.
Dalam erti kata lain, model akan mempertimbangkan kedua-dua hubungan temporal dan spatial. Ini ialah idea teras Spacetimeformer: gunakan model untuk mengeksploitasi hubungan ruang antara bandar/tempat ini, dengan itu mempelajari kebergantungan berguna tambahan kerana model akan mengambil kira kedua-dua hubungan temporal dan ruang.
Kaji dengan mendalam jujukan ruang-masa
Seperti namanya, model ini menggunakan struktur berdasarkan transformer secara dalaman. Apabila menggunakan model berasaskan transformer untuk ramalan siri masa, teknik popular untuk menghasilkan benam sedar masa adalah dengan menghantar input melalui lapisan pembenaman Time2Vec [6] (untuk tugas NLP, vektor pengekodan kedudukan digunakan dan bukannya Time2Vec). Walaupun teknik ini berfungsi dengan baik untuk siri masa univariate, ia tidak masuk akal untuk input masa multivariate. Mungkin dalam pemodelan bahasa, setiap perkataan dalam ayat diwakili oleh pembenaman, dan perkataan pada dasarnya adalah sebahagian daripada perbendaharaan kata, manakala siri masa tidak begitu mudah.
Dalam siri masa multivariate, pada langkah masa tertentu t, input adalah dalam bentuk x_1,t, x2,t, x_m,t di mana x_i,t ialah nilai ciri i dan m ialah ciri/ Jumlah bilangan jujukan. Jika kita menghantar input melalui lapisan Time2Vec, vektor benam temporal akan dihasilkan. Apakah yang sebenarnya diwakili oleh pembenaman ini? Jawapannya ialah ia akan mewakili keseluruhan koleksi input sebagai satu entiti (token). Jadi model hanya akan mempelajari dinamik temporal antara langkah masa tetapi akan terlepas hubungan spatial antara ciri/pembolehubah.
Spacetimeformer menyelesaikan masalah ini dengan meratakan input menjadi satu vektor besar, dipanggil jujukan ruang masa. Jika input mengandungi pembolehubah N, disusun ke dalam langkah masa T, urutan spatiotemporal yang terhasil akan mempunyai label (NxT). Rajah 3 di bawah menunjukkan ini dengan lebih baik:
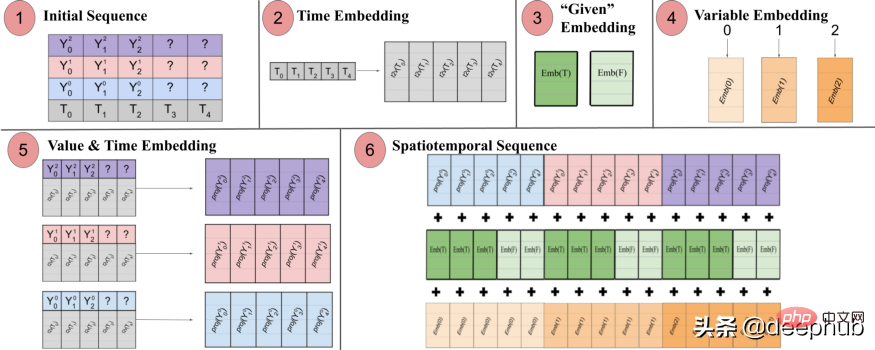
Kertas itu menyatakan: "(1) Format input berbilang variasi yang mengandungi maklumat masa. Input penyahkod tiada nilai ("?") dan ditetapkan kepada sifar apabila membuat ramalan. (2) Siri masa dilalui melalui Lapisan Time2Vec, menghasilkan pembenaman Frekuensi yang mewakili corak input berkala (3) Benamkan binari menunjukkan sama ada nilai diberikan sebagai konteks atau perlu diramalkan (4) Memetakan indeks integer setiap siri masa kepada perwakilan "ruang". pembenaman jadual carian dan ruang pembolehubah. Urutan yang panjang diambil sebagai input
Dalam erti kata lain, urutan terakhir mengekodkan pembenaman bersatu yang mengandungi maklumat temporal, ruang dan kontekstual tetapi kelemahan kaedah ini ialah urutan tersebut sangat panjang. Menghasilkan pertumbuhan kuadratik sumber Ini kerana mengikut mekanisme perhatian, setiap token disemak dengan yang lain
Temporal Fusion TransformerTemporal Fusion Transformer (TFT) ialah model ramalan siri masa berasaskan Transformer yang dikeluarkan oleh Google lebih serba boleh berbanding model sebelumnya >Peringkat teratas seni bina TFT ditunjukkan dalam Rajah 4. Berikut ialah kelebihan utama model ini: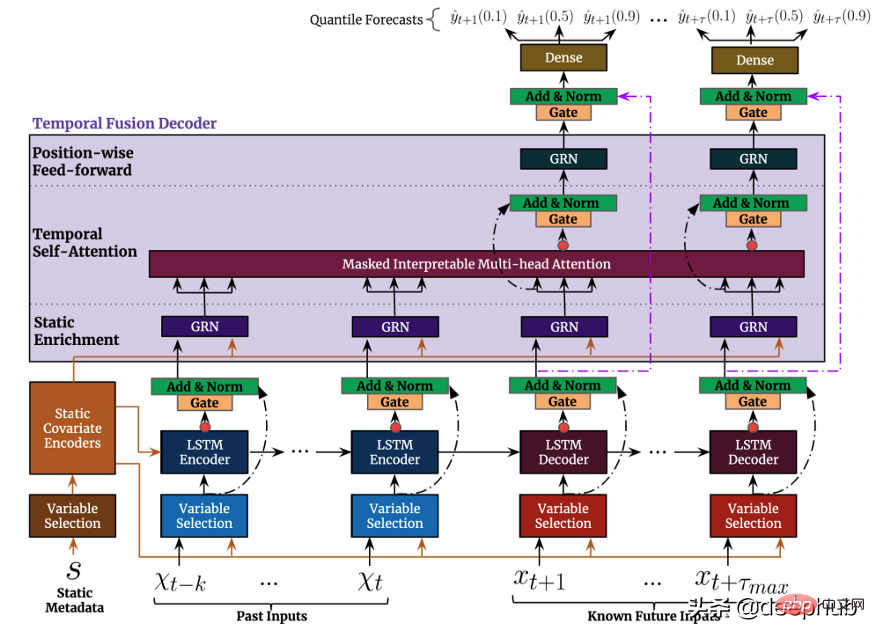 Seperti model yang dinyatakan sebelum ini, TFT menyokong pembinaan pada beberapa siri masa yang heterogen
Seperti model yang dinyatakan sebelum ini, TFT menyokong pembinaan pada beberapa siri masa yang heterogen
Sokongan TFT tiga jenis ciri: i) Data pembolehubah masa dengan input masa hadapan yang diketahui ii) Data pembolehubah masa yang diketahui hanya setakat ini iii) Pembolehubah kategori/statik, juga dikenali sebagai ciri invarian masa oleh itu TFT lebih serba boleh berbanding model sebelumnya . Dalam senario ramalan permintaan kuasa yang dinyatakan sebelum ini, kami ingin menggunakan tahap kelembapan sebagai ciri pembolehubah masa, yang tidak diketahui dalam TFT sehingga kini boleh dilaksanakan, tetapi tidak dalam DeepAR ciri-ciri ini: TFT memberi penekanan yang kuat pada kebolehtafsiran Secara khusus, dengan memanfaatkan komponen Pemilihan Pembolehubah (ditunjukkan dalam Rajah 4 di atas), model itu boleh mengukur kesan setiap ciri ciri. TFT, sebaliknya Mekanisme perhatian berbilang kepala yang boleh ditafsirkan baru dicadangkan: pemberat perhatian lapisan ini boleh mendedahkan langkah masa yang paling penting dalam tempoh semakan ini corak bermusim dalam keseluruhan set data 🎜>Selang ramalan: Sama seperti DeepAR, TFT mengeluarkan selang ramalan dan nilai ramalan dengan menggunakan regresi kuantil. . Sebagai tambahan kepada prestasi mereka yang tiada tandingan, semua model di atas mempunyai satu persamaan: mereka menggunakan sepenuhnya data temporal berbilang variasi dan mereka menggunakan maklumat eksogen untuk meningkatkan prestasi ramalan ke tahap yang tidak pernah berlaku sebelum ini. Walau bagaimanapun, kebanyakan tugas pemprosesan bahasa semula jadi (NLP) menggunakan model pra-latihan. Suapan tugas NLP kebanyakannya adalah data yang dicipta oleh manusia Ia penuh dengan maklumat yang kaya dan sangat baik dan hampir boleh dianggap sebagai unit data. Dalam ramalan siri masa, kita dapat merasakan kekurangan model pra-latihan tersebut. Mengapa kita tidak boleh memanfaatkan ini dalam siri masa seperti yang kita lakukan dalam NLP?
Ini membawa kepada model terakhir yang ingin kami perkenalkan, TSFormer Model ini mempertimbangkan dua perspektif Kami membahagikannya kepada empat bahagian daripada input kepada output, dan menyediakan kod pelaksanaan Python (secara rasmi juga disediakan ), model ini baru dikeluarkan, jadi kami memfokuskannya di sini.
TSFormer
Ia ialah model pra-latihan siri masa tanpa pengawasan berdasarkan Transformer (TSFormer), yang menggunakan strategi latihan dalam MAE dan mampu menangkap kebergantungan yang sangat lama dalam data.
NLP dan Siri Masa: 
Data siri masa kurang padat daripada Bahasa semula jadi data jauh lebih rendah
Kami memerlukan data siri masa yang lebih panjang daripada data NLP
Pengenalan kepada TSFormerTSFormer pada dasarnya serupa dengan seni bina utama MAE, data Lulus melalui pengekod dan kemudian melalui penyahkod, matlamat utama adalah untuk membina semula data yang hilang (bertopeng buatan).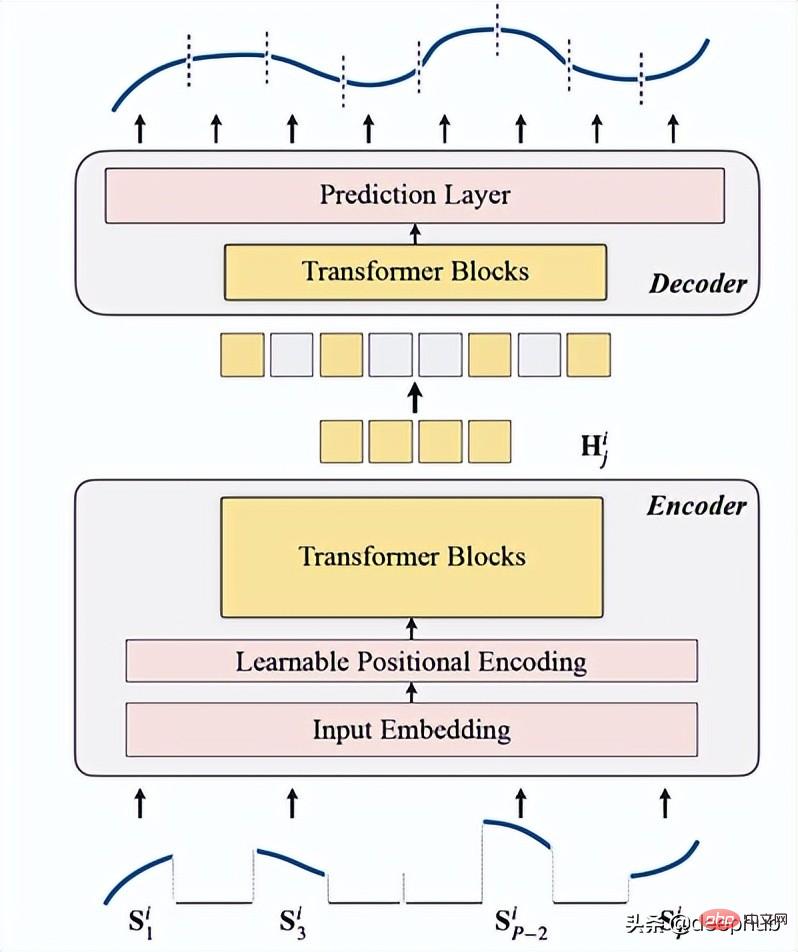
Kami meringkaskannya kepada 4 perkara berikut:
1. Menyamarkan
berfungsi sebagai langkah pertama sebelum data memasuki pengekod. Urutan input (Sᶦ) telah diedarkan ke dalam kepingan P, yang panjangnya ialah L. Oleh itu, panjang tetingkap gelongsor yang digunakan untuk meramalkan langkah seterusnya ialah P XL.

Nisbah oklusi ialah 75% (nampak sangat tinggi, saya rasa ia menggunakan parameter yang sama seperti MAE yang ingin kami selesaikan ialah tugasan yang diselia sendiri); jadi semakin tinggi data Semakin sedikit pengekod semakin cepat pengiraan.
Sebab utama melakukan ini (menolim segmen jujukan input) ialah tampung
- lebih baik daripada titik individu.
- Ia memudahkan penggunaan model hiliran (STGNN mengambil segmen unit sebagai input)
- Ia boleh menguraikan saiz input pengekod.
class Patch(nn.Module):<br>def __init__(self, patch_size, input_channel, output_channel, spectral=True):<br>super().__init__()<br>self.output_channel = output_channel<br>self.P = patch_size<br>self.input_channel = input_channel<br>self.output_channel = output_channel<br>self.spectral = spectral<br>if spectral:<br>self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)<br>else:<br>self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))<br>def forward(self, input):<br>B, N, C, L = input.shape<br>if self.spectral:<br>spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)<br>real = spec_feat_.real<br>imag = spec_feat_.imag<br>spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)<br>output = self.emb_layer(spec_feat).transpose(-1, -2)<br>else:<br>input = input.unsqueeze(-1) # B, N, C, L, 1<br>input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1<br>output = self.input_embedding(input) # B*N, d, L/P, 1<br>output = output.squeeze(-1).view(B, N, self.output_channel, -1)<br>assert output.shape[-1] == L / self.P<br>return output
Berikut ialah fungsi yang menjana masking:
class MaskGenerator(nn.Module):<br>def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):<br>super().__init__()<br>self.mask_size = mask_size<br>self.mask_ratio = mask_ratio<br>self.sort = True<br>self.average_patch = lm<br>self.distribution = distribution<br>if self.distribution == "geom":<br>assert lm != -1<br>assert distribution in ['geom', 'uniform']<br>def uniform_rand(self):<br>mask = list(range(int(self.mask_size)))<br>random.shuffle(mask)<br>mask_len = int(self.mask_size * self.mask_ratio)<br>self.masked_tokens = mask[:mask_len]<br>self.unmasked_tokens = mask[mask_len:]<br>if self.sort:<br>self.masked_tokens = sorted(self.masked_tokens)<br>self.unmasked_tokens = sorted(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def geometric_rand(self):<br>mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked<br>self.masked_tokens = np.where(mask)[0].tolist()<br>self.unmasked_tokens = np.where(~mask)[0].tolist()<br># assert len(self.masked_tokens) > len(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def forward(self):<br>if self.distribution == 'geom':<br>self.unmasked_tokens, self.masked_tokens = self.geometric_rand()<br>elif self.distribution == 'uniform':<br>self.unmasked_tokens, self.masked_tokens = self.uniform_rand()<br>else:<br>raise Exception("ERROR")<br>return self.unmasked_tokens, self.masked_tokens2. Pengekodan
termasuk pembenaman input, pengekodan kedudukan dan blok Transformer. Pengekod hanya boleh dilaksanakan pada patch yang tidak bertopeng (ini juga kaedah MAE).
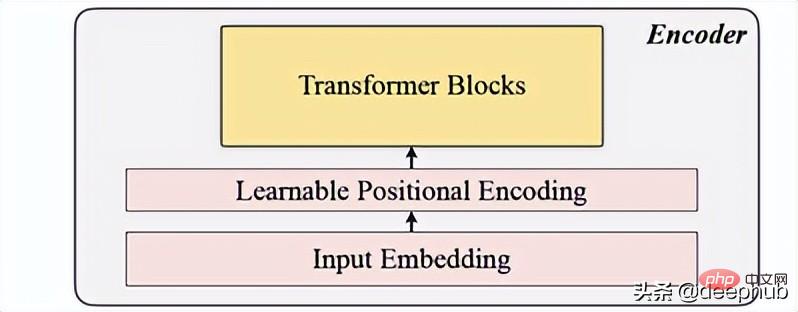
Pembenaman input
Gunakan unjuran linear untuk mendapatkan pembenaman input, yang menukarkan ruang yang tidak bertopeng kepada ruang terpendam. Formulanya boleh dilihat di bawah:
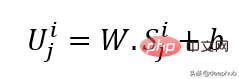
W dan B ialah parameter yang boleh dipelajari dan U ialah vektor input model dalam dimensi.
Pengekodan kedudukan
Lapisan pengekodan kedudukan mudah digunakan untuk menambahkan maklumat jujukan baharu. Menambah perkataan "boleh dipelajari", yang membantu menunjukkan prestasi yang lebih baik daripada sinus. Oleh itu, pembenaman lokasi yang boleh dipelajari menunjukkan hasil yang baik untuk siri masa.
class LearnableTemporalPositionalEncoding(nn.Module):<br>def __init__(self, d_model, dropout=0.1, max_len: int = 1000):<br>super().__init__()<br>self.dropout = nn.Dropout(p=dropout)<br>self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)<br>nn.init.uniform_(self.pe, -0.02, 0.02)<br><br>def forward(self, X, index):<br>if index is None:<br>pe = self.pe[:X.size(1), :].unsqueeze(0)<br>else:<br>pe = self.pe[index].unsqueeze(0)<br>X = X + pe<br>X = self.dropout(X)<br>return X<br>class PositionalEncoding(nn.Module):<br>def __init__(self, hidden_dim, dropout=0.1):<br>super().__init__()<br>self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)<br>def forward(self, input, index=None, abs_idx=None):<br>B, N, L_P, d = input.shape<br># temporal embedding<br>input = self.tem_pe(input.view(B*N, L_P, d), index=index)<br>input = input.view(B, N, L_P, d)<br># absolute positional embedding<br>return input
Blok Transformer
Kertas menggunakan 4 lapisan Transformer, iaitu nombor yang lebih rendah daripada biasa dalam penglihatan komputer dan tugas pemprosesan bahasa semula jadi. Transformer yang digunakan di sini ialah struktur paling asas yang disebut dalam kertas asal, seperti yang ditunjukkan dalam Rajah 4 di bawah:
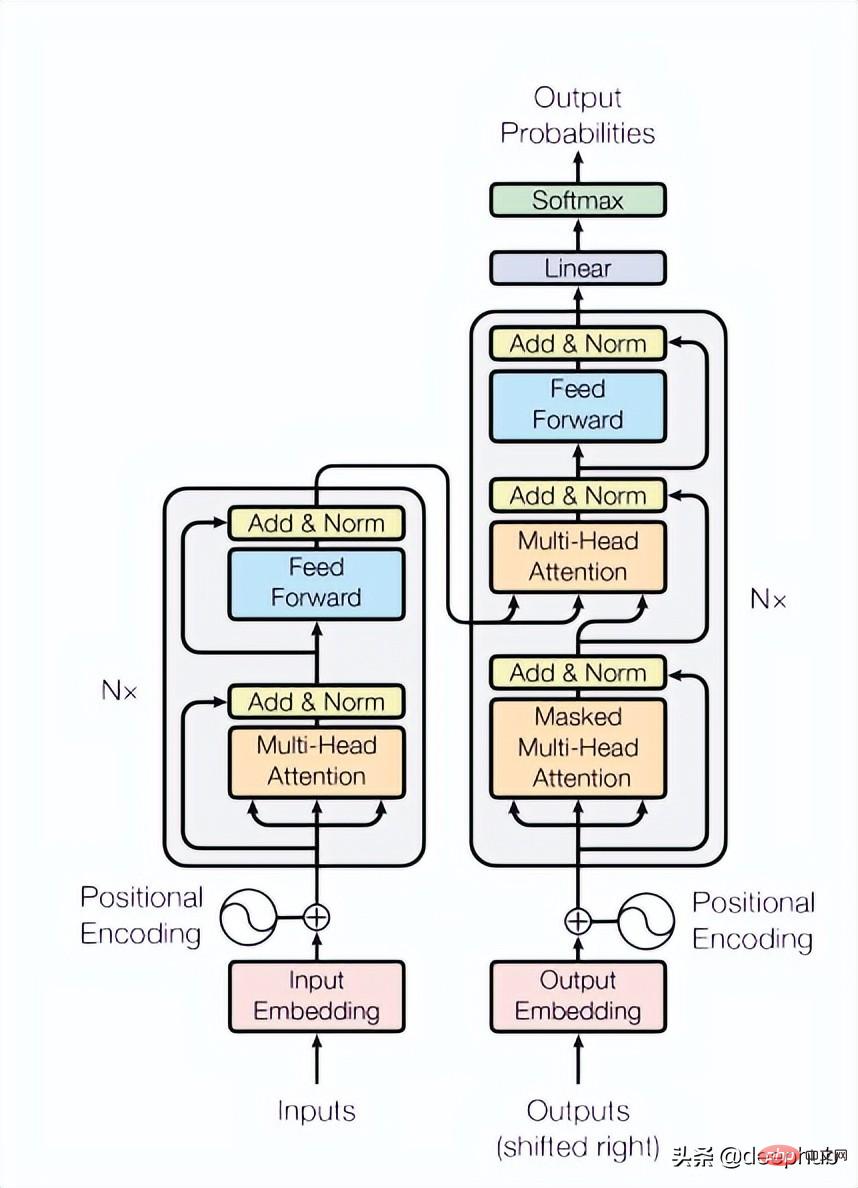
class TransformerLayers(nn.Module):<br>def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):<br>super().__init__()<br>self.d_model = hidden_dim<br>encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)<br>self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)<br>def forward(self, src):<br>B, N, L, D = src.shape<br>src = src * math.sqrt(self.d_model)<br>src = src.view(B*N, L, D)<br>src = src.transpose(0, 1)<br>output = self.transformer_encoder(src, mask=None)<br>output = output.transpose(0, 1).view(B, N, L, D)<br>return output
3
Penyahkod terdiri daripada satu siri blok Transformer. Ia digunakan untuk semua tampalan (sebaliknya, MAE tidak mempunyai pembenaman kedudukan, kerana tampalannya sudah mempunyai maklumat kedudukan), dan bilangan lapisan hanya satu, dan kemudian menggunakan MLP mudah, yang menjadikan panjang output sama dengan setiap tampalan. panjang. 
Kira patch topeng untuk setiap titik data (i), dan pilih mae (Min-Mutlak-Ralat) sebagai fungsi Kehilangan untuk urutan utama dan urutan yang dibina semula. 
Ini ialah keseluruhan seni bina 
Berikut ialah pelaksanaan kod: 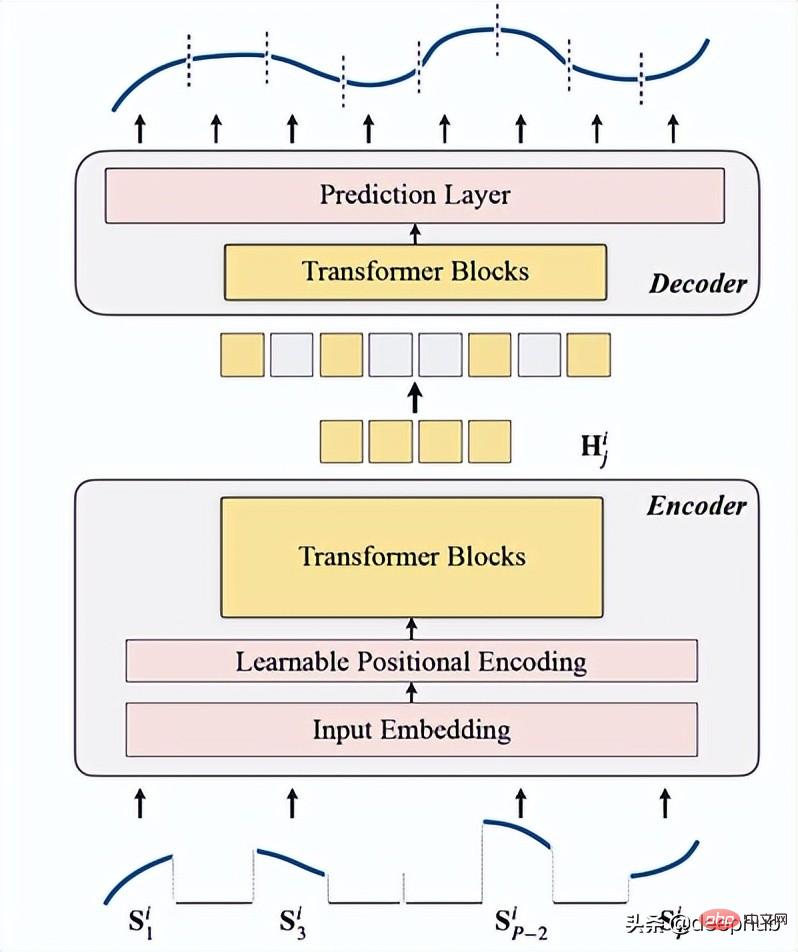
def trunc_normal_(tensor, mean=0., std=1.):<br>__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)<br>def unshuffle(shuffled_tokens):<br>dic = {}<br>for k, v, in enumerate(shuffled_tokens):<br>dic[v] = k<br>unshuffle_index = []<br>for i in range(len(shuffled_tokens)):<br>unshuffle_index.append(dic[i])<br>return unshuffle_index<br>class TSFormer(nn.Module):<br>def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):<br>super().__init__()<br>self.patch_size = patch_size<br>self.seleted_feature = selected_feature<br>self.mode = mode<br>self.spectral = spectral<br>self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)<br>self.pe = PositionalEncoding(out_channel, dropout=dropout)<br>self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)<br>self.encoder = TransformerLayers(out_channel, L)<br>self.decoder = TransformerLayers(out_channel, 1)<br>self.encoder_2_decoder = nn.Linear(out_channel, out_channel)<br>self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))<br>trunc_normal_(self.mask_token, std=.02)<br>if self.spectral:<br>self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)<br>else:<br>self.output_layer = nn.Linear(out_channel, patch_size)<br>def _forward_pretrain(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br><br># mask tokens<br>unmasked_token_index, masked_token_index = self.mask()<br>encoder_input = patches[:, :, unmasked_token_index, :] <br># encoder<br>H = self.encoder(encoder_input) <br># encoder to decoder<br>H = self.encoder_2_decoder(H)<br># decoder<br># H_unmasked = self.pe(H, index=unmasked_token_index)<br>H_unmasked = H<br>H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)<br>H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d<br>H = self.decoder(H_full)<br># output layer<br>if self.spectral:<br># output = H<br>spec_feat_H_ = self.output_layer(H)<br>real = spec_feat_H_[..., :int(self.patch_size/2+1)]<br>imag = spec_feat_H_[..., int(self.patch_size/2+1):]<br>spec_feat_H = torch.complex(real, imag)<br>out_full = torch.fft.irfft(spec_feat_H)<br>else:<br>out_full = self.output_layer(H)<br># prepare loss<br>B, N, _, _ = out_full.shape <br>out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]<br>out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)<br>label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P<br>label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()<br>label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)<br># prepare plot<br>## note that the output_full and label_full are not aligned. The out_full in shuffled<br>### therefore, unshuffle for plot<br>unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)<br>out_full_unshuffled = out_full[:, :, unshuffled_index, :]<br>plot_args = {}<br>plot_args['out_full_unshuffled'] = out_full_unshuffled<br>plot_args['label_full'] = label_full<br>plot_args['unmasked_token_index'] = unmasked_token_index<br>plot_args['masked_token_index'] = masked_token_index<br>return out_masked_tokens, label_masked_tokens, plot_args<br>def _forward_backend(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br>encoder_input = patches # no mask when running the backend.<br># encoder<br>H = self.encoder(encoder_input) <br>return H<br>def forward(self, input_data):<br><br>if self.mode == 'Pretrain':<br>return self._forward_pretrain(input_data)<br>else:<br>return self._forward_backend(input_data)Atas ialah kandungan terperinci Ringkasan perbandingan lima model pembelajaran mendalam untuk ramalan siri masa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1371
1371
 52
52
 Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Ditulis sebelum ini, hari ini kita membincangkan bagaimana teknologi pembelajaran mendalam boleh meningkatkan prestasi SLAM berasaskan penglihatan (penyetempatan dan pemetaan serentak) dalam persekitaran yang kompleks. Dengan menggabungkan kaedah pengekstrakan ciri dalam dan pemadanan kedalaman, di sini kami memperkenalkan sistem SLAM visual hibrid serba boleh yang direka untuk meningkatkan penyesuaian dalam senario yang mencabar seperti keadaan cahaya malap, pencahayaan dinamik, kawasan bertekstur lemah dan seks yang teruk. Sistem kami menyokong berbilang mod, termasuk konfigurasi monokular, stereo, monokular-inersia dan stereo-inersia lanjutan. Selain itu, ia juga menganalisis cara menggabungkan SLAM visual dengan kaedah pembelajaran mendalam untuk memberi inspirasi kepada penyelidikan lain. Melalui percubaan yang meluas pada set data awam dan data sampel sendiri, kami menunjukkan keunggulan SL-SLAM dari segi ketepatan kedudukan dan keteguhan penjejakan.
 Regresi kuantil untuk ramalan kebarangkalian siri masa
May 07, 2024 pm 05:04 PM
Regresi kuantil untuk ramalan kebarangkalian siri masa
May 07, 2024 pm 05:04 PM
Jangan ubah maksud kandungan asal, perhalusi kandungan, tulis semula kandungan dan jangan teruskan. "Regression kuantil memenuhi keperluan ini, menyediakan selang ramalan dengan peluang yang dikira. Ia adalah teknik statistik yang digunakan untuk memodelkan hubungan antara pembolehubah peramal dan pembolehubah tindak balas, terutamanya apabila taburan bersyarat pembolehubah tindak balas adalah menarik Apabila. Tidak seperti regresi tradisional kaedah, regresi kuantil memfokuskan pada menganggar magnitud bersyarat pembolehubah bergerak balas dan bukannya min bersyarat "Rajah (A): Regresi kuantil Regresi kuantil ialah anggaran. Kaedah pemodelan untuk hubungan linear antara set regresi X dan kuantil. daripada pembolehubah yang dijelaskan Y. Model regresi yang sedia ada sebenarnya adalah kaedah untuk mengkaji hubungan antara pembolehubah yang dijelaskan dan pembolehubah penjelasan. Mereka memberi tumpuan kepada hubungan antara pembolehubah penjelasan dan pembolehubah yang dijelaskan
 Menerobos sempadan pengesanan kecacatan tradisional, 'Spektrum Kecacatan' mencapai ketepatan ultra tinggi dan pengesanan kecacatan industri semantik yang kaya buat kali pertama.
Jul 26, 2024 pm 05:38 PM
Menerobos sempadan pengesanan kecacatan tradisional, 'Spektrum Kecacatan' mencapai ketepatan ultra tinggi dan pengesanan kecacatan industri semantik yang kaya buat kali pertama.
Jul 26, 2024 pm 05:38 PM
Dalam pembuatan moden, pengesanan kecacatan yang tepat bukan sahaja kunci untuk memastikan kualiti produk, tetapi juga teras untuk meningkatkan kecekapan pengeluaran. Walau bagaimanapun, set data pengesanan kecacatan sedia ada selalunya tidak mempunyai ketepatan dan kekayaan semantik yang diperlukan untuk aplikasi praktikal, menyebabkan model tidak dapat mengenal pasti kategori atau lokasi kecacatan tertentu. Untuk menyelesaikan masalah ini, pasukan penyelidik terkemuka yang terdiri daripada Universiti Sains dan Teknologi Hong Kong Guangzhou dan Teknologi Simou telah membangunkan set data "DefectSpectrum" secara inovatif, yang menyediakan anotasi berskala besar yang kaya dengan semantik bagi kecacatan industri. Seperti yang ditunjukkan dalam Jadual 1, berbanding set data industri lain, set data "DefectSpectrum" menyediakan anotasi kecacatan yang paling banyak (5438 sampel kecacatan) dan klasifikasi kecacatan yang paling terperinci (125 kategori kecacatan
 Model dialog NVIDIA ChatQA telah berkembang kepada versi 2.0, dengan panjang konteks disebut pada 128K
Jul 26, 2024 am 08:40 AM
Model dialog NVIDIA ChatQA telah berkembang kepada versi 2.0, dengan panjang konteks disebut pada 128K
Jul 26, 2024 am 08:40 AM
Komuniti LLM terbuka ialah era apabila seratus bunga mekar dan bersaing Anda boleh melihat Llama-3-70B-Instruct, QWen2-72B-Instruct, Nemotron-4-340B-Instruct, Mixtral-8x22BInstruct-v0.1 dan banyak lagi. model yang cemerlang. Walau bagaimanapun, berbanding dengan model besar proprietari yang diwakili oleh GPT-4-Turbo, model terbuka masih mempunyai jurang yang ketara dalam banyak bidang. Selain model umum, beberapa model terbuka yang mengkhusus dalam bidang utama telah dibangunkan, seperti DeepSeek-Coder-V2 untuk pengaturcaraan dan matematik, dan InternVL untuk tugasan bahasa visual.
 Google AI memenangi pingat perak IMO Mathematical Olympiad, model penaakulan matematik AlphaProof telah dilancarkan dan pembelajaran pengukuhan kembali
Jul 26, 2024 pm 02:40 PM
Google AI memenangi pingat perak IMO Mathematical Olympiad, model penaakulan matematik AlphaProof telah dilancarkan dan pembelajaran pengukuhan kembali
Jul 26, 2024 pm 02:40 PM
Bagi AI, Olimpik Matematik tidak lagi menjadi masalah. Pada hari Khamis, kecerdasan buatan Google DeepMind menyelesaikan satu kejayaan: menggunakan AI untuk menyelesaikan soalan sebenar IMO Olimpik Matematik Antarabangsa tahun ini, dan ia hanya selangkah lagi untuk memenangi pingat emas. Pertandingan IMO yang baru berakhir minggu lalu mempunyai enam soalan melibatkan algebra, kombinatorik, geometri dan teori nombor. Sistem AI hibrid yang dicadangkan oleh Google mendapat empat soalan dengan betul dan memperoleh 28 mata, mencapai tahap pingat perak. Awal bulan ini, profesor UCLA, Terence Tao baru sahaja mempromosikan Olimpik Matematik AI (Anugerah Kemajuan AIMO) dengan hadiah berjuta-juta dolar Tanpa diduga, tahap penyelesaian masalah AI telah meningkat ke tahap ini sebelum Julai. Lakukan soalan secara serentak pada IMO Perkara yang paling sukar untuk dilakukan dengan betul ialah IMO, yang mempunyai sejarah terpanjang, skala terbesar dan paling negatif
 Pandangan alam semula jadi: Ujian kecerdasan buatan dalam perubatan berada dalam keadaan huru-hara Apa yang perlu dilakukan?
Aug 22, 2024 pm 04:37 PM
Pandangan alam semula jadi: Ujian kecerdasan buatan dalam perubatan berada dalam keadaan huru-hara Apa yang perlu dilakukan?
Aug 22, 2024 pm 04:37 PM
Editor |. ScienceAI Berdasarkan data klinikal yang terhad, beratus-ratus algoritma perubatan telah diluluskan. Para saintis sedang membahaskan siapa yang harus menguji alat dan cara terbaik untuk melakukannya. Devin Singh menyaksikan seorang pesakit kanak-kanak di bilik kecemasan mengalami serangan jantung semasa menunggu rawatan untuk masa yang lama, yang mendorongnya untuk meneroka aplikasi AI untuk memendekkan masa menunggu. Menggunakan data triage daripada bilik kecemasan SickKids, Singh dan rakan sekerja membina satu siri model AI untuk menyediakan potensi diagnosis dan mengesyorkan ujian. Satu kajian menunjukkan bahawa model ini boleh mempercepatkan lawatan doktor sebanyak 22.3%, mempercepatkan pemprosesan keputusan hampir 3 jam bagi setiap pesakit yang memerlukan ujian perubatan. Walau bagaimanapun, kejayaan algoritma kecerdasan buatan dalam penyelidikan hanya mengesahkan perkara ini
 Latihan dengan berjuta-juta data kristal untuk menyelesaikan masalah fasa kristalografi, kaedah pembelajaran mendalam PhAI diterbitkan dalam Sains
Aug 08, 2024 pm 09:22 PM
Latihan dengan berjuta-juta data kristal untuk menyelesaikan masalah fasa kristalografi, kaedah pembelajaran mendalam PhAI diterbitkan dalam Sains
Aug 08, 2024 pm 09:22 PM
Editor |KX Sehingga hari ini, perincian dan ketepatan struktur yang ditentukan oleh kristalografi, daripada logam ringkas kepada protein membran yang besar, tidak dapat ditandingi oleh mana-mana kaedah lain. Walau bagaimanapun, cabaran terbesar, yang dipanggil masalah fasa, kekal mendapatkan maklumat fasa daripada amplitud yang ditentukan secara eksperimen. Penyelidik di Universiti Copenhagen di Denmark telah membangunkan kaedah pembelajaran mendalam yang dipanggil PhAI untuk menyelesaikan masalah fasa kristal Rangkaian saraf pembelajaran mendalam yang dilatih menggunakan berjuta-juta struktur kristal tiruan dan data pembelauan sintetik yang sepadan boleh menghasilkan peta ketumpatan elektron yang tepat. Kajian menunjukkan bahawa kaedah penyelesaian struktur ab initio berasaskan pembelajaran mendalam ini boleh menyelesaikan masalah fasa pada resolusi hanya 2 Angstrom, yang bersamaan dengan hanya 10% hingga 20% daripada data yang tersedia pada resolusi atom, manakala Pengiraan ab initio tradisional
 Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) set data memainkan peranan penting dalam mempromosikan penyelidikan pemprosesan bahasa semula jadi (NLP). Set data QA berkualiti tinggi bukan sahaja boleh digunakan untuk memperhalusi model, tetapi juga menilai dengan berkesan keupayaan model bahasa besar (LLM), terutamanya keupayaan untuk memahami dan menaakul tentang pengetahuan saintifik. Walaupun pada masa ini terdapat banyak set data QA saintifik yang meliputi bidang perubatan, kimia, biologi dan bidang lain, set data ini masih mempunyai beberapa kekurangan. Pertama, borang data adalah agak mudah, kebanyakannya adalah soalan aneka pilihan. Ia mudah dinilai, tetapi mengehadkan julat pemilihan jawapan model dan tidak dapat menguji sepenuhnya keupayaan model untuk menjawab soalan saintifik. Sebaliknya, Soal Jawab terbuka



