
Ringkasnya: Rekursi ialah apabila kaedah memanggil dirinya sendiri, menghantar pembolehubah berbeza setiap kali ia dipanggil Rekursi membantu pengaturcara menyelesaikan masalah yang rumit dan menjadikan kod itu ringkas.
Lihat senario aplikasi praktikal, masalah maze (backtracking), rekursi (Recursion)
Saya akan senaraikan dua kes kecil , Untuk membantu anda memahami rekursif, berikut ialah semakan mekanisme panggilan rekursif
Masalah cetak
Masalah faktor
public static void test(int n) {
if (n > 2) {
test(n - 1);
}
System.out.println("n=" + n);
}
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1) * n;
}
}Apakah jenis masalah yang digunakan rekursi untuk diselesaikan?
Pelbagai masalah matematik seperti: masalah 8 ratu, Menara Hanoi, faktorial masalah, maze Masalah, masalah bola dan bakul (pertandingan pengaturcaraan google).
Rekursi juga digunakan dalam pelbagai algoritma, seperti isihan pantas, isihan gabungan, carian binari, algoritma bahagi dan takluk, dsb.
Masalah yang akan diselesaikan dengan timbunan-->Kod ketiga agak ringkas.
Peraturan penting yang perlu dipatuhi untuk rekursi
Apabila kaedah dilaksanakan, ruang bebas terlindung baharu (ruang tindanan) dicipta.
Pembolehubah tempatan kaedah adalah bebas dan tidak akan mempengaruhi satu sama lain, seperti pembolehubah n.
Jika pembolehubah jenis rujukan (seperti tatasusunan) digunakan dalam kaedah, data jenis rujukan akan dikongsi.
Rekursi mesti mendekati syarat untuk keluar dari rekursi, jika tidak, ia akan menjadi rekursi tak terhingga, StackOverflowError akan muncul, dan anda akan mati :).
Apabila kaedah menyelesaikan pelaksanaan atau menemui pengembalian, hasilnya akan dikembalikan kepada sesiapa yang memanggilnya Pada masa yang sama, apabila kaedah menyelesaikan pelaksanaan atau mengembalikan, kaedah itu juga akan kembali.
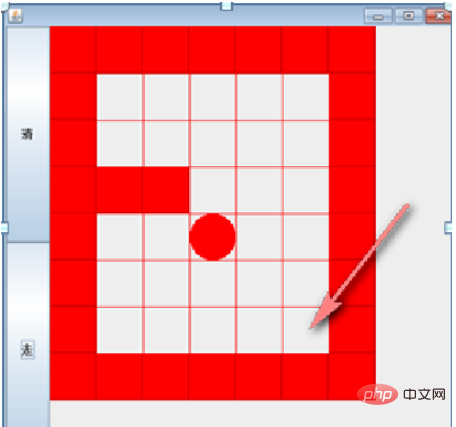
Penjelasan: Laluan yang dilalui oleh bola, dan pencarian laluan yang ditetapkan oleh pengaturcara Strategi adalah berkaitan dengan: susunan atas, bawah, kiri dan kanan apabila mencari laluan berkaitan Apabila anda mendapat laluan bola, anda boleh mula-mula menggunakan (kanan bawah, kiri atas), dan kemudian menukarnya kepada (atas kanan, kiri bawah) untuk melihat sama ada laluan berubah. Uji untuk fenomena menjejak ke belakang.
package com.szh.recursion;
/**
* 走迷宫问题
*/
public class MiGong {
//使用递归回溯来给小球找路, 说明:
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置,则说明通路找到.
//4. 约定:当 map[i][j] 为 0 表示该点没有走过; 当为 1 表示墙; 2 表示通路可以走;
//5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
public static boolean setWay(int[][] map, int i, int j) {
//此时走到了迷宫终点
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2;
if (setWay(map, i + 1, j)) { //下
return true;
} else if (setWay(map, i, j + 1)) { //右
return true;
} else if (setWay(map, i - 1, j)) { //上
return true;
} else { //左
return true;
}
} else { //map[i][j] != 0, 即只能为1、2。 1表示墙(无法走),2表示已经走过了,所以此时直接返回false
return false;
}
}
}
//修改找路的策略,改成 上->右->下->左
public static boolean setWay2(int[][] map, int i, int j) {
if(map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if(map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 上->右->下->左
map[i][j] = 2;
if(setWay2(map, i - 1, j)) { //上
return true;
} else if (setWay2(map, i, j + 1)) { //右
return true;
} else if (setWay2(map, i + 1, j)) { //下
return true;
} else { //左
return true;
}
} else {
return false;
}
}
}
public static void main(String[] args) {
//先创建一个二维数组,模拟迷宫 (地图)
int[][] map = new int[8][7];
//使用迷宫中的部分格子表示墙体(置1)
//第一行和最后一行置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//第一列和最后一列置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//多添加两块墙体
map[3][1] = 1;
map[3][2] = 1;
// map[1][2] = 1;
// map[2][2] = 1;
//输出地图查看
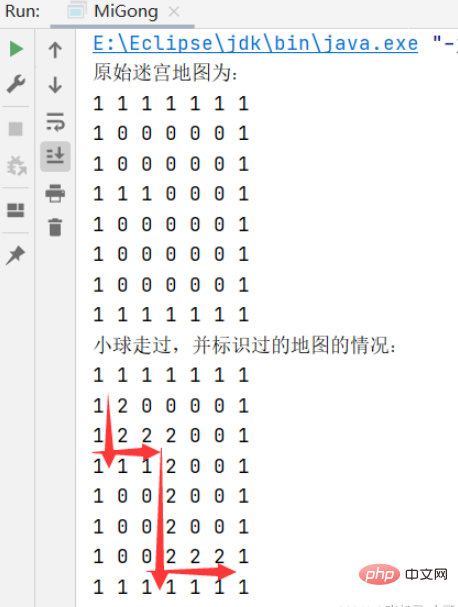
System.out.println("原始迷宫地图为:");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//使用递归回溯走迷宫
setWay(map, 1, 1);
// setWay2(map, 1, 1);
System.out.println("小球走过,并标识过的地图的情况:");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
}
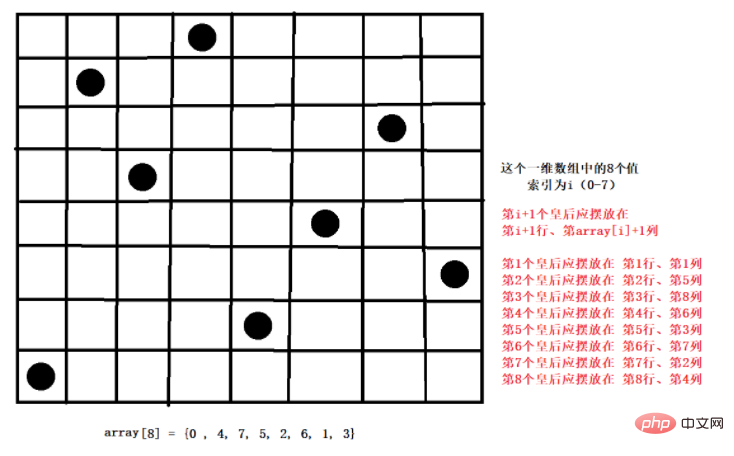
The Eight Queens Problem is an kuno dan terkenal The masalah ialah kes biasa algoritma penjejakan ke belakang. Masalah ini dibangkitkan oleh pemain catur antarabangsa Max Bethel pada tahun 1848: Letakkan lapan ratu pada grid catur 8×8 supaya mereka tidak boleh menyerang antara satu sama lain, iaitu, tiada dua ratu boleh berada dalam kedudukan yang sama dalam baris, lajur atau pepenjuru?

Ratu pertama diletakkan di baris pertama dan lajur pertama dahulu.
Letakkan ratu kedua di baris kedua dan lajur pertama, dan kemudian tentukan sama ada ia OK Jika tidak, teruskan letakkannya dalam lajur kedua dan lajur ketiga untuk mencari a yang sesuai.
Teruskan ke ratu ketiga, atau lajur pertama, lajur kedua... sehingga ratu ke-8 boleh diletakkan pada kedudukan yang tidak bercanggah, ia boleh dianggap sebagai penyelesaian yang betul.
Apabila penyelesaian yang betul diperolehi, apabila tindanan bergolek kembali ke tindanan sebelumnya, ia akan mula menjejak ke belakang, iaitu meletakkan ratu pertama dalam lajur pertama, dan semua penyelesaian yang betul akan diperolehi.
Kemudian kembali dan teruskan meletakkan ratu pertama dalam lajur kedua, dan kemudian teruskan melakukan langkah 1, 2, 3, dan 4 dalam gelung.
package com.szh.recursion;
/**
* 八皇后问题
*/
public class Queue8 {
//定义max表示共有多少个皇后
private int max = 8;
//定义数组,保存皇后放置的位置结果,比如 arr = {0, 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
//共有多少种解法
private static int count = 0;
//共有多少次冲突
private static int judgeCount = 0;
//编写一个方法,放置第n个皇后
//特别注意: check 是 每一次递归时,进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯
private void check(int n) {
if (n == max) { //n = 8 , 表示这8个皇后已经全部放好了
print();
return;
}
//依次放入皇后,并判断是否冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if (judge(n)) { // 不冲突
//接着放n+1个皇后,即开始递归
check(n + 1);
}
//如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行第i列向后的那一列
}
}
//查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的n-1个皇后冲突
private boolean judge(int n) {
//每摆放一个皇后,就循环去和之前摆好的皇后位置相比较,看是否冲突
for (int i = 0; i < n; i++) {
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
//3. 判断是否在同一行, 没有必要,n 表示第几个皇后,这个值每次都在递增,所以必然不在同一行
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
judgeCount++;
return false;
}
}
return true;
}
//打印皇后摆放的具体位置
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法\n", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount);
}
}
Malah, anda boleh melihat proses penjejakan ke belakang dengan menyahpepijat kod di sini, jadi saya tidak akan memberitahu lebih lanjut.
Atas ialah kandungan terperinci Cara menggunakan struktur dan algoritma data Java untuk melaksanakan rekursi dan penjejakan ke belakang. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




