
Tulis atur cara yang boleh melukis segi tiga sama, dan pada setiap sisi segi tiga, ia mesti boleh melukis segitiga luar yang lebih kecil. Mampu mengulangi proses ini seberapa banyak yang dikehendaki mencipta beberapa corak yang menarik.
Mewakili imej sebagai tatasusunan piksel dua dimensi. Setiap sel dalam tatasusunan piksel akan mewakili warna (RGB) piksel tersebut.
Untuk melakukan ini, anda boleh menggunakan perpustakaan NumPy untuk menjana tatasusunan piksel dan Bantal untuk menukarnya kepada imej yang boleh disimpan.
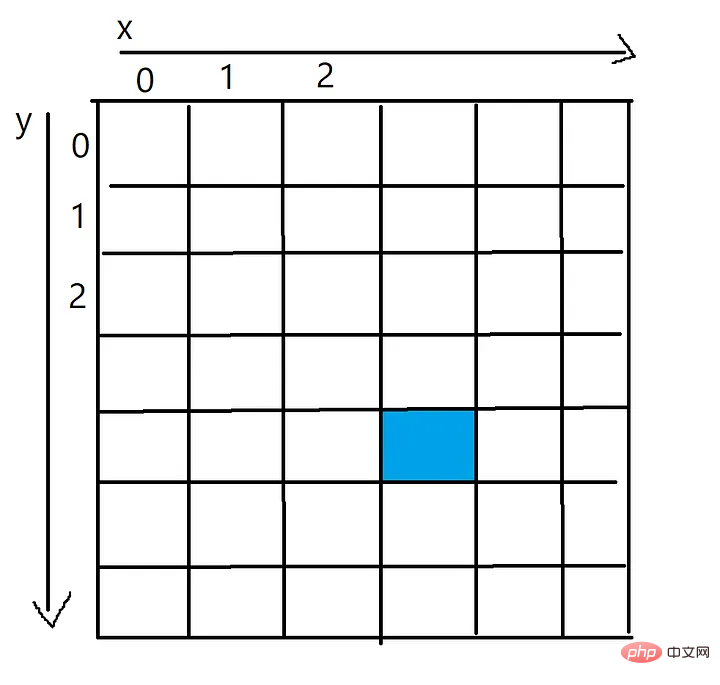
Nilai x bagi piksel biru ialah 3 dan nilai y ialah 4, yang boleh diakses melalui tatasusunan dua dimensi, seperti piksel[4][3 ]
Sekarang mulakan pengekodan Pertama, anda memerlukan fungsi yang boleh mendapatkan dua set koordinat dan lukis garisan di antaranya.
Kod di bawah berfungsi dengan menginterpolasi antara dua titik, menambahkan piksel baharu pada tatasusunan piksel pada setiap langkah. Anda boleh menganggap proses ini sebagai teduhan piksel demi piksel pada baris.
Anda boleh menggunakan aksara sambungan "" dalam setiap coretan kod untuk menampung beberapa baris kod yang lebih panjang.
import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
# 找出像素阵列的边界
max_x_coordinate = len(pixels[0])
max_y_coordinate = len(pixels)
# 两点之间沿着x轴和y轴的距离
horizontal_distance = to_coordinates[1] - from_coordinates[1]
vertical_distance = to_coordinates[0] - from_coordinates[0]
# 两点之间的总距离
distance = math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
+ (to_coordinates[0] - from_coordinates[0])**2)
# 每次给一个新的像素上色时,将向前走多远
horizontal_step = horizontal_distance/distance
vertical_step = vertical_distance/distance
# 此时,将进入循环以在像素数组中绘制线
# 循环的每一次迭代都会沿着线添加一个新的点
for i in range(round(distance)):
# 这两个坐标是直线中心的坐标
current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
# 一旦得到了点的坐标,
# 就在坐标周围画出尺寸为thickness的图案
for x in range (-thickness, thickness):
for y in range (-thickness, thickness):
x_value = current_x_coordinate + x
y_value = current_y_coordinate + y
if (x_value > 0 and x_value < max_x_coordinate and \
y_value > 0 and y_value < max_y_coordinate):
pixels[y_value][x_value] = colour
# 定义图像的大小
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# 画一条线
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# 把像素阵列变成一张真正的图片
img = Image.fromarray(pixels)
# 显示得到的图片,并保存它
img.show()
img.save('Line.png')
Hasil fungsi ini apabila melukis garis kuning di antara setiap sudut tatasusunan piksel
Sekarang kita mempunyai fungsi yang melukis garis antara dua titik, kita boleh melukis segitiga sama sisi pertama kita.
Memandangkan titik tengah dan panjang sisi segitiga, ketinggian boleh dikira menggunakan formula: h = ½(√3a).
Kini dengan menggunakan ketinggian, titik tengah dan panjang sisi ini, anda boleh mengira kedudukan setiap sudut segitiga. Menggunakan fungsi plot_line yang kami buat tadi, kami boleh melukis garisan antara setiap sudut.
def draw_triangle(center, side_length, thickness, colour, pixels):
# 等边三角形的高度是,h = ½(√3a)
# 其中a是边长
triangle_height = round(side_length * math.sqrt(3)/2)
# 顶角
top = [center[0] - triangle_height/2, center[1]]
# 左下角
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# 右下角
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
# 在每个角之间画一条线来完成三角形
plot_line(top, bottom_left, thickness, colour, pixels)
plot_line(top, bottom_right, thickness, colour, pixels)
plot_line(bottom_left, bottom_right, thickness, colour, pixels)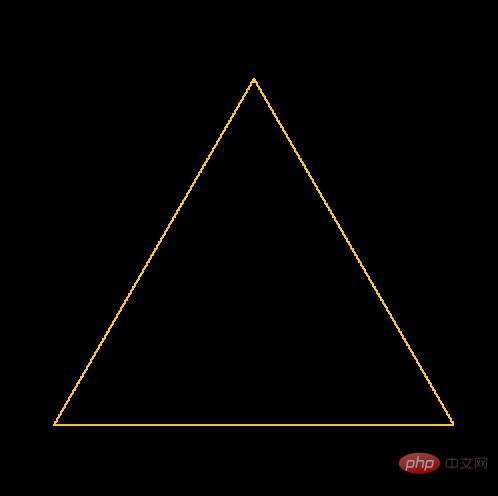
Hasilnya apabila melukis segitiga di tengah PNG 500x500 piksel
Semuanya sudah sedia, anda boleh Cipta fraktal pertama anda dalam Python.
Tetapi langkah terakhir adalah yang paling sukar untuk diselesaikan, fungsi segi tiga memanggil dirinya sendiri untuk setiap sisinya, seseorang perlu dapat mengira titik tengah setiap segitiga baru yang lebih kecil dan memutarkannya dengan betul supaya ia berserenjang kepada mereka Bahagian yang melekat.
Anda boleh menggunakan fungsi ini untuk memutar setiap sudut segitiga dengan menolak offset titik tengah daripada koordinat yang diputar dan kemudian menggunakan formula untuk memutarkan sepasang koordinat.
def rotate(coordinate, center_point, degrees):
# 从坐标中减去旋转的点
x = (coordinate[0] - center_point[0])
y = (coordinate[1] - center_point[1])
# Python的cos和sin函数采用弧度而不是度数
radians = math.radians(degrees)
# 计算旋转点
new_x = (x * math.cos(radians)) - (y * math.sin(radians))
new_y = (y * math.cos(radians)) + (x * math.sin(radians))
# 将在开始时减去的偏移量加回旋转点上
return [new_x + center_point[0], new_y + center_point[1]]
Putar setiap koordinat 35 darjah segitiga
Setelah anda boleh memutarkan segitiga, fikirkan cara melukis pada setiap sisi segitiga pertama A segitiga kecil baru.
Untuk mencapai ini, lanjutkan fungsi draw_triangle untuk mengira putaran dan titik tengah segitiga baharu bagi setiap sisi, yang panjang sisinya dikurangkan dengan parameter shrink_side_by.
Sebaik sahaja ia mengira titik tengah dan putaran segitiga baharu, ia memanggil draw_triangle(diri) untuk melukis segitiga baharu yang lebih kecil dari tengah garisan semasa. Ini kemudiannya akan memukul blok kod yang sama secara terbalik untuk mengira satu lagi set titik tengah dan putaran untuk segi tiga yang lebih kecil.
Ini dipanggil algoritma gelung kerana fungsi draw_triangle kini memanggil dirinya sendiri sehingga mencapai kedalaman maksimum segi tiga yang ingin dilukis. Mempunyai ayat melarikan diri ini adalah penting kerana secara teorinya fungsi akan bergelung selama-lamanya (tetapi dalam praktiknya timbunan panggilan akan menjadi terlalu besar, menyebabkan ralat limpahan timbunan).
def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \
pixels, shrink_side_by, iteration, max_depth):
# 等边三角形的高度是,h = ½(√3a)
# 其中'a'是边长
triangle_height = side_length * math.sqrt(3)/2
# 顶角
top = [center[0] - triangle_height/2, center[1]]
# 左下角
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# 右下角
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
if (degrees_rotate != 0):
top = rotate(top, center, degrees_rotate)
bottom_left = rotate(bottom_left, center, degrees_rotate)
bottom_right = rotate(bottom_right, center, degrees_rotate)
# 三角形各边之间的坐标
lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]]
line_number = 0
# 在每个角之间画一条线来完成三角形
for line in lines:
line_number += 1
plot_line(line[0], line[1], thickness, colour, pixels)
# 如果还没有达到max_depth,就画一些新的三角形
if (iteration < max_depth and (iteration < 1 or line_number < 3)):
gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1])
new_side_length = side_length*shrink_side_by
# 正在绘制的三角形线的中心
center_of_line = [(line[0][0] + line[1][0]) / 2, \
(line[0][1] + line[1][1]) / 2]
new_center = []
new_rotation = degrees_rotate
# 需要旋转traingle的数量
if (line_number == 1):
new_rotation += 60
elif (line_number == 2):
new_rotation -= 60
else:
new_rotation += 180
# 在一个理想的世界里,这将是gradient=0,
# 但由于浮点除法的原因,无法
# 确保永远是这种情况
if (gradient < 0.0001 and gradient > -0.0001):
if (center_of_line[0] - center[0] > 0):
new_center = [center_of_line[0] + triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
new_center = [center_of_line[0] - triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
# 计算直线梯度的法线
difference_from_center = -1/gradient
# 计算这条线距中心的距离
# 到新三角形的中心
distance_from_center = triangle_height * (shrink_side_by/2)
# 计算 x 方向的长度,
# 从线的中心到新三角形的中心
x_length = math.sqrt((distance_from_center**2)/ \
(1 + difference_from_center**2))
# 计算出x方向需要走哪条路
if (center_of_line[1] < center[1] and x_length > 0):
x_length *= -1
# 现在计算Y方向的长度
y_length = x_length * difference_from_center
# 用新的x和y值来偏移线的中心
new_center = [center_of_line[0] + y_length, \
center_of_line[1] + x_length]
draw_triangle(new_center, new_side_length, new_rotation, \
thickness, colour, pixels, shrink_side_by, \
iteration+1, max_depth)
Fraktal segi tiga, sisi mengecut=1/2, kedalaman maksimum=2
Atas ialah kandungan terperinci Bagaimana untuk melukis corak fraktal menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




