Apakah algoritma biasa yang biasa digunakan dalam pembangunan Java?

Algoritma tamak

Aplikasi klasik: seperti Pengekodan Huffman, algoritma pepohon rentang minimum Prim dan Kruskal serta algoritma laluan terpendek sumber tunggal Dijkstra.

Langkah-langkah algoritma tamak untuk menyelesaikan masalah

Langkah pertama, apabila kita melihat masalah seperti ini, kita mesti terlebih dahulu memikirkan algoritma tamak: untuk satu set data, kita menentukan nilai had dan nilai yang dijangkakan, dengan harapan dapat memilih beberapa data daripada ia, dan memuaskan Dalam kes mengehadkan nilai, nilai yang dijangkakan adalah yang terbesar.

Secara analogi dengan contoh tadi, nilai had ialah berat tidak boleh melebihi 100kg, dan nilai yang dijangkakan ialah jumlah nilai item. Set data ini ialah 5 jenis kacang. Kami memilih sebahagian daripadanya yang beratnya tidak melebihi 100kg dan mempunyai jumlah nilai yang paling besar.

Dalam langkah kedua, kami cuba melihat sama ada masalah ini boleh diselesaikan dengan algoritma tamak: setiap kali, pilih data yang menyumbang paling banyak kepada nilai yang dijangkakan di bawah situasi semasa dan menyumbang jumlah yang sama kepada nilai had.

Secara analogi dengan contoh tadi, kami memilih kacang dengan harga seunit tertinggi daripada baki kacang setiap kali, iaitu kacang yang menyumbang paling banyak kepada nilai apabila berat ialah sama.

Dalam langkah ketiga, kami memberikan beberapa contoh untuk melihat sama ada keputusan yang dihasilkan oleh algoritma tamak adalah optimum. Dalam kebanyakan kes, hanya berikan beberapa contoh untuk mengesahkannya. Membuktikan dengan tegas ketepatan algoritma tamak adalah sangat rumit dan memerlukan banyak penaakulan matematik.

Sebab utama algoritma tamak tidak berfungsi ialah pilihan sebelumnya akan mempengaruhi pilihan berikutnya.

Analisis Praktikal Algoritma Tamak

1

Kami mempunyai m gula-gula dan n kanak-kanak. Kami kini ingin mengagihkan gula-gula kepada kanak-kanak ini, tetapi gula-gula kurang dan lebih ramai kanak-kanak (m

Kita boleh abstrak masalah ini kepada: daripada n kanak-kanak, pilih beberapa kanak-kanak untuk mengedarkan gula-gula, supaya bilangan kanak-kanak yang berpuas hati (nilai jangkaan) adalah yang terbesar. Nilai had masalah ini ialah bilangan gula-gula m.

Setiap kali, kami mencari yang mempunyai permintaan terkecil untuk saiz gula-gula di kalangan kanak-kanak yang tinggal, dan kemudian memberinya gula-gula terkecil antara gula-gula yang tinggal yang boleh memuaskannya Pelan pengedaran yang diperolehi dengan cara ini adalah The rancangan yang memuaskan bilangan kanak-kanak yang paling ramai.

2

Masalah ini lebih kerap berlaku dalam kehidupan seharian kita. Katakan kita mempunyai wang kertas 1 yuan, 2 yuan, 5 yuan, 10 yuan, 20 yuan, 50 yuan dan 100 yuan masing-masing ialah c1, c2, c5, c10, c20, c50 dan c100. Kita kini perlu menggunakan wang ini untuk membayar K yuan Berapakah jumlah wang kertas minimum yang perlu kita gunakan?

Dalam kehidupan, kita mesti membayar dengan yang mempunyai nilai muka yang paling besar dahulu Jika tidak mencukupi, kita akan terus menggunakan yang mempunyai nilai muka yang lebih kecil, dan seterusnya, dan akhirnya menggunakan 1 yuan. untuk membuat selebihnya. Dalam kes menyumbang nilai jangkaan yang sama (bilangan wang kertas), kami berharap dapat menyumbang lebih banyak, supaya jumlah wang kertas dapat dikurangkan Ini adalah penyelesaian kepada algoritma yang tamak.

3. Liputan selang waktu

Andaikan kita mempunyai n selang, dan titik permulaan dan penamat bagi selang itu ialah [l1, r1], [l2, r2], [l3, r3], ..., [ln, rn] masing-masing . Kami memilih sebahagian daripada selang daripada n selang ini. Bahagian selang ini memenuhi bahawa setiap pasangan selang tidak bersilang (titik akhir bersilang tidak dianggap sebagai persilangan paling banyak?

Idea pemprosesan ini digunakan dalam banyak masalah algoritma yang tamak, seperti penjadualan tugas, penjadualan guru, dsb.

Penyelesaian kepada masalah ini adalah seperti berikut: kami menganggap bahawa titik akhir paling kiri bagi n selang ini ialah lmin dan titik akhir paling kanan ialah rmax. Masalah ini bersamaan dengan memilih beberapa selang cerai dan menutup [lmin, rmax] dari kiri ke kanan. Kami menyusun n selang ini mengikut tertib daripada titik akhir permulaan yang kecil ke yang besar.

Setiap kali kami memilih, titik akhir kiri tidak bertepatan dengan selang yang dilindungi sebelum ini, dan titik akhir yang betul adalah sekecil mungkin, supaya selang yang tidak bertutup boleh diletakkan seluas yang mungkin. Ini sebenarnya kaedah pemilihan yang tamak.

Bagaimana untuk melaksanakan pengekodan Huffman menggunakan algoritma tamak?

Pengekodan Huffman menggunakan kaedah pengekodan tidak sama panjang ini untuk mengekod aksara. Diperlukan bahawa antara pengekodan setiap aksara, tidak akan ada situasi di mana satu pengekodan adalah awalan pengekodan yang lain. Gunakan pengekodan yang lebih pendek sedikit untuk aksara yang muncul lebih kerap;

Andaikan saya mempunyai fail yang mengandungi 1000 aksara Setiap aksara menduduki 1 bait (1byte=8bits Ia memerlukan sejumlah 8000bit untuk menyimpan 1000 aksara ini?

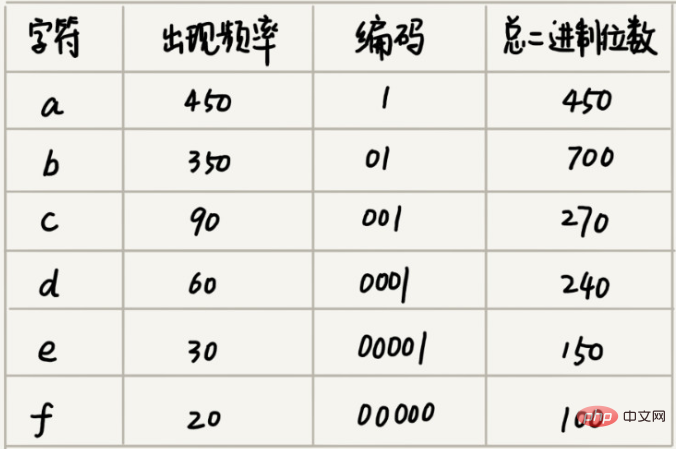
Andaikan kita dapati melalui analisis statistik bahawa 1000 aksara ini hanya mengandungi 6 aksara yang berbeza, andaikan ia adalah a, b, c, d, e dan f. 3 bit binari (bit) boleh mewakili 8 aksara yang berbeza Oleh itu, untuk meminimumkan ruang storan, kami menggunakan 3 bit binari untuk mewakili setiap aksara. Kemudian hanya memerlukan 3000 bit untuk menyimpan 1000 aksara ini, yang menjimatkan banyak ruang daripada kaedah penyimpanan asal. Walau bagaimanapun, adakah terdapat kaedah penyimpanan yang lebih menjimatkan ruang?

a(000), b(001), c(010), d(011), e(100), f(101)

Pengekodan Huffman ialah kaedah pengekodan yang sangat berkesan dan digunakan secara meluas dalam pemampatan data biasanya antara 20% dan 90%.

Pengekodan Huffman bukan sahaja meneliti bilangan aksara berbeza yang terdapat dalam teks, tetapi juga meneliti kekerapan kejadian setiap aksara dan memilih kod dengan panjang yang berbeza berdasarkan kekerapan. Pengekodan Huffman cuba menggunakan kaedah pengekodan panjang tidak sama ini untuk meningkatkan lagi kecekapan pemampatan. Bagaimana untuk memilih kod panjang yang berbeza untuk aksara dengan frekuensi yang berbeza? Berdasarkan pemikiran tamak, kita boleh menggunakan kod yang lebih pendek sedikit untuk aksara yang muncul lebih kerap;

Kod tersebut mempunyai panjang yang berbeza.

Untuk pengekodan sama panjang, sangat mudah untuk kami menyahmampatkannya. Sebagai contoh, dalam contoh tadi, kita menggunakan 3 bit untuk mewakili aksara. Apabila menyahmampat, kami membaca kod binari 3 digit daripada teks setiap kali dan menterjemahkannya ke dalam aksara yang sepadan. Walau bagaimanapun, kod Huffman tidak sama panjang Adakah 1 bit dibaca setiap kali, atau 2 bit, 3 bit, dsb. untuk penyahmampatan? Masalah ini menjadikan pengekodan Huffman lebih rumit untuk dinyahmampatkan. Untuk mengelakkan kekaburan semasa proses penyahmampatan, Pengekodan Huffman memerlukan antara pengekodan setiap aksara, tidak akan ada situasi di mana satu pengekodan ialah awalan pengekodan yang lain.

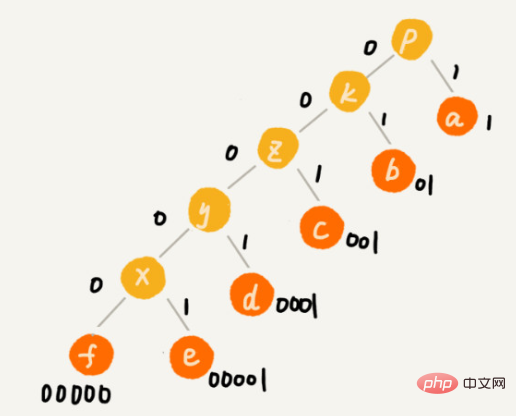
Andaikan bahawa kekerapan kejadian 6 aksara ini dari tinggi ke rendah ialah a, b, c, d, e, f. Kami mengekodnya seperti ini Pengekodan mana-mana aksara bukan awalan yang lain Apabila menyahmampat, kami akan membaca rentetan perduaan boleh nyahmampat yang mungkin setiap kali, jadi kami tidak akan ada kekaburan. Selepas pengekodan dan pemampatan ini, 1000 aksara ini hanya memerlukan 2100 bit.

Walaupun idea pengekodan Huffman tidak sukar difahami, Bagaimana untuk mengekod aksara yang berbeza dengan panjang yang berbeza mengikut kekerapan kejadiannya?

Gunakan tindanan besar untuk meletakkan aksara mengikut kekerapan.

Algoritma Bahagi dan Takluk

Idea teras algoritma divide and conquer sebenarnya adalah empat perkataan, divide and conquer, iaitu, membahagikan masalah asal kepada n sub-masalah yang lebih kecil dengan struktur yang serupa dengan masalah asal, secara rekursif Menyelesaikan submasalah ini dan kemudian menggabungkan keputusannya menghasilkan penyelesaian kepada masalah asal.

Algoritma divide-and-conquer ialah idea penyelesaian masalah, dan rekursi ialah teknik pengaturcaraan. Malah, algoritma bahagi-dan-takluk secara amnya lebih sesuai untuk dilaksanakan menggunakan rekursi. Dalam pelaksanaan rekursif algoritma bahagi-dan-takluk, setiap peringkat rekursi melibatkan tiga operasi berikut:

• Uraian: Uraikan masalah asal kepada satu siri sub-masalah; -masalah cukup kecil, maka penyelesaian langsung

• Gabung: gabungkan hasil sub-masalah ke dalam masalah asal.

• Masalah yang boleh diselesaikan oleh algoritma bahagi-dan-takluk secara amnya perlu memenuhi syarat berikut:

Masalah asal mempunyai corak yang sama dengan masalah kecil yang diuraikan; boleh diselesaikan secara bebas, dan sub-masalah boleh diselesaikan secara bebas Tiada korelasi antara

• mempunyai keadaan penamatan penguraian, iaitu apabila masalah cukup kecil, ia boleh diselesaikan secara langsung;

• boleh dibahagikan kepada Masalah digabungkan ke dalam masalah asal, dan kerumitan operasi gabungan ini tidak boleh terlalu tinggi, jika tidak, ia tidak akan mempunyai kesan mengurangkan kerumitan keseluruhan algoritma.

• Contoh analisis aplikasi algoritma bahagi dan takluk

• Bagaimana untuk memprogramkan untuk mencari bilangan pasangan tertib atau pasangan terbalik set data?

  Bandingkan setiap nombor dengan nombor selepasnya untuk melihat bilangan yang lebih kecil daripadanya. Kami merekodkan bilangan nombor yang lebih kecil daripadanya sebagai k Dengan cara ini, selepas memeriksa setiap nombor, kami merumuskan nilai k yang sepadan dengan setiap nombor. Walau bagaimanapun, kerumitan masa operasi ini ialah O(n^2).

  Kita boleh membahagikan tatasusunan kepada dua bahagian, A1 dan A2, mengira bilangan pasangan tertib terbalik K1 dan K2 bagi A1 dan A2 masing-masing, dan kemudian mengira bilangan pasangan tertib terbalik K3 antara A1 dan A2. Maka bilangan pasangan tertib terbalik dalam tatasusunan A adalah sama dengan K1+K2+K3. Dengan bantuan algoritma isihan gabungan

  Adakah terdapat keperluan untuk mengisih fail pesanan 10GB mengikut jumlah?

  Kami boleh mengimbas pesanan terlebih dahulu dan membahagikan fail 10GB kepada beberapa julat amaun berdasarkan jumlah pesanan. Sebagai contoh, jumlah pesanan antara 1 dan 100 yuan diletakkan dalam fail kecil, jumlah pesanan antara 101 dan 200 diletakkan dalam fail lain, dan seterusnya. Dengan cara ini, setiap fail kecil boleh dimuatkan ke dalam memori untuk diisih secara berasingan, dan akhirnya fail kecil yang dipesan ini digabungkan untuk mendapatkan data pesanan 10GB pesanan terakhir.

  Algoritma penjejakan belakang

  Senario aplikasi: carian mendalam-dahulu, padanan ungkapan biasa, analisis sintaks dalam prinsip kompilasi. Banyak masalah matematik klasik boleh diselesaikan menggunakan algoritma backtracking, seperti Sudoku, lapan ratu, ransel 0-1, pewarna graf, masalah jurujual perjalanan, pilih atur jumlah, dll.

  Idea pemprosesan menjejak ke belakang agak serupa dengan carian penghitungan. Kami menghitung semua penyelesaian dan mencari penyelesaian yang memenuhi jangkaan kami. Untuk selalu menghitung semua penyelesaian yang mungkin dan mengelakkan peninggalan dan pertindihan, kami membahagikan proses penyelesaian masalah kepada beberapa peringkat. Pada setiap peringkat, kami akan menghadapi persimpangan di jalan Kami mula-mula memilih laluan secara rawak Apabila kami mendapati bahawa laluan ini tidak berfungsi (tidak memenuhi penyelesaian yang diharapkan), kami kembali ke persimpangan sebelumnya di jalan itu. pilih jalan lain Teruskan berjalan.

  Masalah Lapan Ratu

  Kami mempunyai papan catur 8x8, dan kami mahu meletakkan 8 buah catur (ratu) di atasnya. Setiap buah catur tidak boleh mempunyai satu lagi buah catur dalam baris, lajur atau pepenjuru.

  Beg galas 1.0-1

  Banyak senario boleh disarikan ke dalam model masalah ini. Penyelesaian klasik untuk masalah ini ialah pengaturcaraan dinamik, tetapi terdapat juga penyelesaian yang mudah tetapi kurang cekap, iaitu algoritma penjejakan ke belakang yang kita bicarakan hari ini.

  Kami mempunyai beg galas, dan jumlah berat bawaan beg galas itu ialah Wkg. Kini kami mempunyai n item, setiap satunya mempunyai berat yang berbeza dan tidak boleh dibahagikan. Kami kini mahu memilih beberapa item dan memuatkannya ke dalam beg galas kami. Bagaimana untuk memaksimumkan jumlah berat item dalam beg galas tanpa melebihi berat yang boleh dibawa beg galas?

  Untuk setiap item ada dua pilihan, letak dalam beg galas atau tak letak dalam beg galas. Untuk n item, terdapat 2^n cara untuk memasangnya Alih keluar item yang mempunyai jumlah berat melebihi Wkg, dan pilih yang mempunyai jumlah berat paling hampir dengan Wkg daripada kaedah pemasangan yang selebihnya. Namun, bagaimanakah kita boleh menyenaraikan 2^n cara berpura-pura ini secara menyeluruh tanpa pengulangan?

  Kaedah penjejakan belakang: Kami boleh menyusun item mengikut tertib, dan keseluruhan masalah diuraikan kepada n peringkat, dan setiap peringkat sepadan dengan cara memilih item. Proses item pertama dahulu, pilih untuk memuatkannya atau tidak, dan kemudian proses item yang tinggal secara rekursif.

  Pengaturcaraan dinamik

  Pengaturcaraan dinamik lebih sesuai untuk menyelesaikan masalah optimum, seperti mencari nilai maksimum, nilai minimum, dll. Ia boleh mengurangkan kerumitan masa dengan ketara dan meningkatkan kecekapan pelaksanaan kod.

  0-1 Masalah Beg galas

  Untuk satu set item yang tidak boleh dibahagikan dengan berat yang berbeza, kita perlu memilih beberapa untuk dimasukkan ke dalam beg galas Atas alasan untuk memenuhi had berat maksimum beg galas, berapakah jumlah berat maksimum barang tersebut beg galas itu?

  Berfikir:

  (1) Bahagikan keseluruhan proses penyelesaian kepada n peringkat, dan setiap peringkat akan memutuskan sama ada untuk meletakkan item dalam beg galas. Selepas setiap item diputuskan (untuk dimasukkan ke dalam beg galas atau tidak untuk dimasukkan ke dalam beg galas), berat barang dalam beg galas akan mempunyai banyak situasi, iaitu, ia akan mencapai banyak negeri yang berbeza, yang sepadan dengan pokok rekursif, iaitu, terdapat banyak nod yang berbeza.

  (2) Kami menggabungkan keadaan berulang (nod) setiap lapisan, hanya merekodkan keadaan berbeza, dan kemudian memperoleh set keadaan lapisan seterusnya berdasarkan set keadaan lapisan sebelumnya. Kita boleh menggabungkan keadaan berulang bagi setiap lapisan untuk memastikan bilangan keadaan berbeza dalam setiap lapisan tidak melebihi w (w mewakili berat bawaan beg galas), iaitu 9 dalam contoh.

  Bahagikan n peringkat Setiap peringkat diperoleh berdasarkan peringkat sebelumnya dan bergerak ke hadapan secara dinamik untuk mengelakkan pengiraan berulang.

  Kerumitan masa menggunakan algoritma penjejakan ke belakang untuk menyelesaikan masalah ini ialah O(2^n), iaitu eksponen. Jadi apakah kerumitan masa penyelesaian pengaturcaraan dinamik?

  Bahagian yang paling memakan masa ialah gelung dua peringkat dalam kod, jadi kerumitan masa ialah O(n*w). n mewakili bilangan item, dan w mewakili jumlah berat yang boleh dibawa oleh beg galas. Kita perlu memohon tatasusunan dua dimensi tambahan n kali w+1, yang menggunakan banyak ruang. Oleh itu, kadangkala, kita akan mengatakan bahawa pengaturcaraan dinamik adalah penyelesaian yang menukar ruang untuk masa.

  0-1 Masalah Beg galas Versi Dinaik Taraf

  Untuk satu set item yang tidak boleh dibahagikan dengan berat yang berbeza dan nilai yang berbeza, kami memilih untuk meletakkan item tertentu ke dalam beg galas atas alasan untuk memenuhi had berat maksimum beg galas, jumlah nilai item yang boleh dimuatkan ke dalam beg galas adalah yang terbesar.

  Apakah jenis masalah yang sesuai untuk diselesaikan dengan pengaturcaraan dinamik?

  Tiga ciri satu model

  Model: model penyelesaian optimum membuat keputusan berbilang peringkat

  Tiga ciri:

  • Substruktur optimum, penyelesaian optimum masalah mengandungi penyelesaian optimum sub-masalah

  • Tiada kesan sampingan, tahap pertama makna Ya, apabila memperoleh keadaan peringkat kemudian, kami hanya mengambil berat tentang nilai keadaan peringkat sebelumnya, bukan bagaimana keadaan ini diperolehi langkah demi langkah. Maksud kedua ialah apabila status sesuatu peringkat ditentukan, ia tidak akan terjejas oleh keputusan dalam peringkat seterusnya. (Yang terakhir tidak menjejaskan sebelumnya.)

  • Submasalah berulang, urutan keputusan yang berbeza, mungkin menghasilkan keadaan berulang apabila mencapai tahap yang sama.

  Ringkasan dua idea penyelesaian masalah pengaturcaraan dinamik

  1. Nyatakan kaedah jadual peralihan

  Secara amnya, masalah yang boleh diselesaikan dengan pengaturcaraan dinamik boleh diselesaikan dengan carian kekerasan menggunakan algoritma penjejakan belakang. Lukiskan pokok rekursi. Daripada pokok rekursi, kita boleh melihat dengan mudah sama ada terdapat sub-masalah berulang dan bagaimana sub-masalah berulang dijana.

  Selepas mencari sub-masalah pendua, kami mempunyai dua cara untuk menanganinya. Yang pertama adalah dengan terus menggunakan kaedah menjejak ke belakang dan menambah "memo" untuk mengelakkan sub-sub pendua. -masalah. Dari segi kecekapan pelaksanaan, ini tidak berbeza dengan idea penyelesaian pengaturcaraan dinamik. Yang kedua ialah menggunakan penyelesaian pengaturcaraan dinamik, kaedah jadual peralihan nyata.

  Mari kita lukis jadual negeri dahulu. Jadual keadaan biasanya adalah dua dimensi, jadi anda boleh menganggapnya sebagai tatasusunan dua dimensi. Antaranya, setiap keadaan mengandungi tiga pembolehubah, baris, lajur dan nilai tatasusunan. Kami mengisi setiap negeri dalam jadual negeri secara berperingkat mengikut proses membuat keputusan, dari depan ke belakang, dan mengikut hubungan rekursif. Akhir sekali, kami menterjemahkan proses pengisian borang rekursif ini kepada kod, iaitu kod pengaturcaraan dinamik.

  memerlukan banyak pembolehubah untuk diwakili dan jadual keadaan yang sepadan mungkin berdimensi tinggi, seperti tiga dimensi atau empat dimensi. Pada masa ini, kami tidak sesuai menggunakan kaedah jadual peralihan keadaan untuk menyelesaikannya. Di satu pihak, ia adalah kerana jadual peralihan keadaan berdimensi tinggi sukar untuk dilukis dan diwakili, dan sebaliknya, ia adalah kerana otak manusia benar-benar tidak pandai memikirkan perkara berdimensi tinggi.

  2. Nyatakan kaedah persamaan peralihan

  Kita perlu menganalisis bagaimana masalah tertentu boleh diselesaikan secara rekursif melalui sub-masalah, iaitu apa yang dipanggil substruktur optimum. Berdasarkan substruktur optimum, tulis formula rekursif, yang dipanggil persamaan peralihan keadaan. Dengan persamaan peralihan keadaan, pelaksanaan kod adalah sangat mudah. Secara amnya, kami mempunyai dua kaedah pelaksanaan kod, satu ialah rekursi ditambah "memo" dan satu lagi ialah rekursi berulang .

  min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

  Saya ingin menekankan bahawa tidak semua masalah sesuai untuk kedua-dua idea penyelesaian masalah. Sesetengah masalah mungkin lebih jelas dengan cara berfikir yang pertama, dan beberapa masalah mungkin lebih jelas dengan cara pemikiran kedua Oleh itu, anda perlu mempertimbangkan masalah khusus untuk memutuskan kaedah penyelesaian masalah yang akan digunakan.

  Kaedah jadual peralihan keadaanIdea penyelesaian masalah boleh diringkaskan secara kasar sebagai, Pelaksanaan algoritma penjejakan belakang - tentukan keadaan - lukis pepohon rekursi - cari sub-masalah pendua - lukis jadual peralihan keadaan - mengikut rekursi Pengisian borang perhubungan tolak - Terjemahkan proses pengisian borang kepada kod . Idea umum kaedah persamaan peralihan keadaan boleh diringkaskan sebagai, Cari substruktur optimum - tulis persamaan peralihan keadaan - terjemahkan persamaan peralihan keadaan kepada kod.

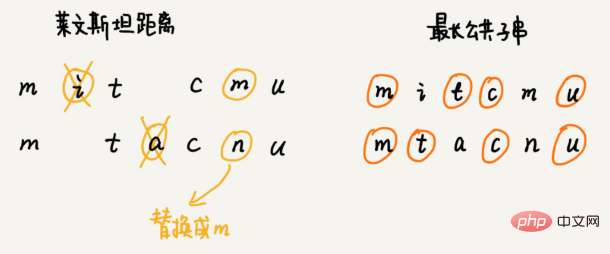
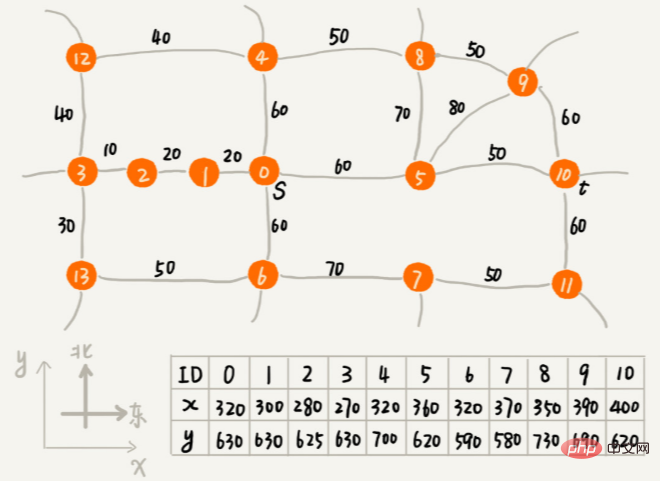
  Bagaimana untuk mengukur persamaan dua rentetan?

  Jarak edit merujuk kepada bilangan minimum operasi pengeditan yang diperlukan untuk menukar satu rentetan kepada rentetan lain (seperti menambah aksara, memadam aksara, menggantikan aksara). Semakin besar jarak suntingan, semakin kecil persamaan antara dua rentetan, sebaliknya, semakin kecil jarak suntingan, semakin besar persamaan antara dua rentetan. Untuk dua rentetan yang sama, jarak edit ialah 0.

  Terdapat banyak kaedah pengiraan yang berbeza untuk jarak edit yang lebih terkenal ialah Jarak Levenshtein, dan Panjang subrentetan biasa terpanjang. Antaranya, jarak Levinstein membenarkan tiga operasi pengeditan menambah, memadam dan menggantikan aksara, dan panjang subrentetan biasa terpanjang hanya membenarkan dua operasi penyuntingan menambah dan memadam aksara.

  Jarak Levenstein dan panjang subrentetan sepunya terpanjang menganalisis persamaan rentetan daripada dua perspektif yang bertentangan sepenuhnya. Saiz jarak Levenstein mewakili perbezaan antara dua rentetan dan saiz subrentetan biasa terpanjang mewakili persamaan antara dua rentetan.
  Jarak Levinstein bagi dua rentetan mitcmu dan mtacnu ialah 3, dan panjang subrentetan sepunya terpanjang ialah 4.

  

  Bagaimana untuk mengira jarak Levenstein secara pemrograman?

  Soalan ini adalah untuk mencari bilangan minimum suntingan yang diperlukan untuk menukar satu rentetan kepada rentetan lain. Keseluruhan proses penyelesaian melibatkan berbilang peringkat membuat keputusan Kita perlu memeriksa secara bergilir sama ada setiap aksara dalam rentetan sepadan dengan aksara dalam rentetan lain, cara menanganinya jika ia sepadan, dan cara menanganinya jika ia tidak sepadan. . Oleh itu, masalah ini mematuhi model penyelesaian optimum pembuatan keputusan berbilang peringkat .

  Algoritma pengesyoran

  Gunakan jarak vektor untuk mencari persamaan.

  

  Cari: Bagaimana untuk menggunakan algoritma carian A* untuk melaksanakan fungsi pencarian laluan dalam permainan?

  Jadi bagaimana untuk mencari laluan sub-optimum dengan cepat yang berhampiran dengan laluan terpendek?

  Algoritma perancangan laluan pantas ini ialah algoritma A* yang akan kita pelajari hari ini. Sebenarnya, algoritma A* ialah pengoptimuman dan transformasi algoritma Dijkstra.

  

  Gunakan jarak garis lurus antara bucu dan titik akhir, iaitu jarak Euclidean, untuk menganggarkan panjang laluan antara bucu dan titik akhir (nota: panjang laluan dan jarak garis lurus ialah dua konsep)

  Jarak ini direkodkan sebagai h(i) (i mewakili nombor bucu ini Nama profesional ialah fungsi heuristik (fungsi heuristik)

  kerana jarak Euclidean Formula pengiraan akan melibatkan pengiraan akar yang memakan masa, jadi kami biasanya menggunakan satu lagi formula pengiraan jarak yang lebih mudah, iaitu jarak Manhattan (jarak Manhattan)

  Jarak Manhattan adalah antara dua titik Jumlah jarak antara koordinat mendatar dan menegak. Proses pengiraan hanya melibatkan penambahan, penolakan dan pembalikan bit tanda, jadi ia lebih cekap daripada jarak Euclidean.

  int hManhattan(Vertex v1, Vertex v2) { // Vertex mewakili bucu, yang ditakrifkan kemudian

  kembalikan Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);

  }

  f(i)=g(i)+h(i), panjang laluan antara bucu dan titik permulaan g(i), anggaran panjang laluan dari bucu ke titik akhir h(i ). f(i ) secara teknikal dipanggil fungsi penilaian.

  Algoritma A* ialah pengubahsuaian mudah algoritma Dijkstra F(i) terkecil disenaraikan dahulu.

  Terdapat tiga perbezaan utama antaranya dan pelaksanaan kod algoritma Dijkstra:

  • Baris gilir keutamaan dibina secara berbeza. Algoritma A* membina baris gilir keutamaan berdasarkan nilai f (iaitu, f(i)=g(i)+h(i) yang baru disebut), manakala algoritma Dijkstra membina baris gilir keutamaan berdasarkan nilai dist ( iaitu, g yang baru disebut (i)) untuk membina baris gilir keutamaan; >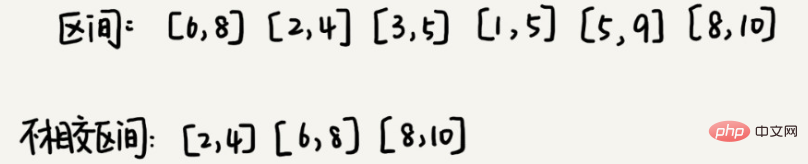

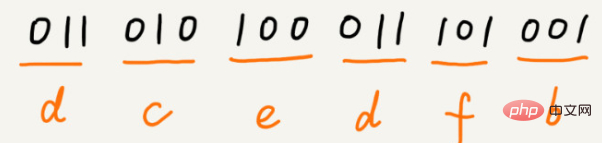
  Syarat untuk gelung berakhir juga berbeza. Algoritma Dijkstra tamat apabila titik akhir dinyah gilir, dan algoritma A* tamat sebaik traversal mencapai titik akhir.

Atas ialah kandungan terperinci Apakah algoritma biasa yang biasa digunakan dalam pembangunan Java?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!