
Pengoptimuman Kawanan Ayam, disingkatkan sebagai CSO (Pengoptimuman Kawanan Ayam), walaupun ia mempunyai latar belakang dalam apa yang dipanggil bionik, pada asasnya adalah varian daripada algoritma kawanan zarah.
Ringkasnya, kawanan zarah adalah sekumpulan zarah Setiap zarah mempunyai kedudukan dan kelajuannya sendiri, dan setiap zarah mesti ditarik oleh zarah terbaik Di samping dua peraturan ini, ia adalah sepenuhnya sama antara satu sama lain, kecuali kedudukan dan kelajuan mereka.
Sudah tentu, algoritma kawanan zarah itu sendiri juga mempunyai latar belakang bionik Dikatakan bahawa ilham itu datang daripada sekumpulan burung yang mencari makanan zarah yang sama bertukar menjadi sekumpulan burung yang sama.
Algoritma kawanan ayam menambah ciri identiti yang berbeza pada zarah ini, atau burung ini, supaya ia tidak lagi setara antara satu sama lain.
Sekurang-kurangnya ada tiga kelas dalam kumpulan ayam iaitu ayam jantan, ayam betina dan anak ayam Setiap ayam mempunyai kedudukan dan kelajuan yang tersendiri. Tetapi bezanya ialah
ayam jantan adalah yang paling tegas merebut makanan, yang bersamaan dengan rawak melukis salah satu ayam jantan lain mempengaruhi kedudukannya.
Ayam-ayam yang paling terkilan Di satu pihak, mereka perlu menerima kepimpinan ayam jantan, dan sebaliknya, mereka perlu bersaing dengan ayam lain untuk mendapatkan makanan<.>
import numpy as np
from random import gauss, random
randint = np.random.randint
uniRand = np.random.uniform
class Chicken:
def __init__(self, N, xRange, order=0, kind=0):
# 生成(N)维参数
self.x = uniRand(*xRange, (N,))
self.best = np.inf
self.xBest = np.zeros((N,))
self.kind = kind # 鸡的类别
self.order = order # 鸡的编号
# 设置自己的首领公鸡
def setCock(self, i):
self.cock = i
# 设置自己的监护母鸡
def setHen(self, i):
self.hen = irandint = np.random.randint
class Swarm:
# cNum 鸡数,是三个元素的列表,分别是公鸡、母鸡和小鸡数
# N参数维度
def __init__(self, cNum, N, xRange):
self.initCs(cNum, N, xRange)
self.bestCS = deepcopy(self.cs) #最佳鸡群
self.best = np.inf #全局最优值
self.xBest = np.zeros((N,)) #全局最优参数
self.N = N
def initCs(self, cNum, N, xRange, vRange):
self.cs = []
self.cNum = cNum
self.cocks = np.arange(cNum[0]) # 公鸡编号
self.hens = np.arange(cNum[0], cNum[0]+cNum[1]) #母鸡编号
self.chicks = np.arange(cNum[0]+cNum[1], np.sum(cNum)) #小鸡编号
kinds = np.repeat([0,1,2], cNum)
for i in range(sum(cNum)):
self.cs.append(Chicken(N,xRange, vRange, i, kinds[i]))
if kinds[i] > 0:
cock = randint(0, cNum[0])
self.cs[i].setCock(cock)
if kinds[i] > 1:
hen = randint(cNum[0], cNum[0]+cNum[1])
self.cs[i].setHen(hen)Ayam jantan
Ingat bahawa nombor ayam jantan semasa ialah i, dan nombor ayam jantan yang dipilih secara rawak ialah j, j≠i, maka kaedah kemas kini kedudukan ayam jantan ke-i Untuk Nombor rawak yang dijana oleh taburan normal boleh dinyatakan sebagai 1∼N(0,σ2
), di mana σ2 ialah
Di mana f secara amnya dipanggil faktor kecergasan, iaitu bersamaan dengan nilai yang diperoleh dengan memasukkan ayam tertentu ke dalam fungsi yang hendak dicari. Contohnya, untuk mencari nilai minimum y=2, jika kedudukan semasa ayam ialah 1.5, maka f=1.52=2.25. ε ialah jumlah kecil yang menghalang ralat pembahagian demi sifar.
Tetapi harus diingat bahawa semua x di atas tidak mewakili skalar, tetapi tatasusunan. 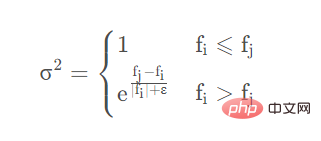
# 写在Swarm类中
def cockStep(self):
for i in self.cocks:
# 第j只公鸡
j = np.random.randint(self.cNum[0])
if j==i:
j = (j+1) % self.cNum[0]
# 第i只公鸡
ci = self.cs[i]
# 第j只公鸡
cj = self.cs[self.cocks[j]]
sigma = 1 if cj.best > ci.best else np.exp(
(cj.best-ci.best)/(np.abs(ci.best)+1e-15))
ci.x *= 1 + gauss(0, sigma)i
(t+1)=xi(t)+k1
r1
(xc&tolak;xi)+k2r2(xj&tolak;x i) Antaranya, xc ialah ayam jantan ketua, dan xj ialah ayam atau ayam jantan yang lain. k1, k2
ialah pekali, dan logik kemas kininya adalah sama dengan ayam jantan Apabila fi lebih besar, ia dinyatakan sebagai Kod ini dilaksanakan sebagai def henStep(self):
nGuarder = self.cNum[0] + self.cNum[1] - 2
for i in self.hens:
guarders = list(self.cocks) + list(self.hens)
c = self.cs[i].cock #首领公鸡
guarders.remove(i)
guarders.remove(c)
# 随机生成另一只监护鸡
j = guarders[np.random.randint(nGuarder)]
ci = self.cs[i]
cj = self.cs[j]
cc = self.cs[c]
k1, k2 = random(), random()
if cc.best > ci.best:
k1 *= np.exp((ci.best-cc.best)/(np.abs(ci.best)+1e-15))
if cj.best < ci.best:
k2 *= np.exp(cj.best-ci.best)
ci.x += k1*(cc.x-ci.x)+k2*(cj.x-ci.x)
Yang terakhir ialah logik kemas kini anak ayam, anak ayam berada di sekeliling ayam Untuk mencari makanan, logik kemas kini ialah 
i
(t+1)=xi(t)+r(x h
( t)&tolak;xi
(t))Antaranya, xh ialah ayam penjaganya, r ialah nombor rawak, dan pelaksanaan algoritma adalah Seluruh kumpulan ayamBak kata pepatah, algoritma berasal dari kehidupan dan lebih tinggi daripada kehidupan Secara semula jadi, kekananan ditekankan, tetapi dalam algoritma kumpulan ayam , penekanan memang pada kekuatan. Jika ayam bertuah dan mendapat hasil pengoptimuman yang lebih baik daripada ayam jantan, maka ayam akan berkembang menjadi ayam jantan.
Dalam erti kata lain, sekali-sekala, identiti ayam dalam kawanan akan disusun semula Yang mempunyai kesan pengoptimuman terbaik ialah ayam jantan ketua, yang lebih teruk adalah ayam penjaga, dan yang paling teruk adalah ayam penjaga. yang paling teruk hanya boleh menjadi ayam jantan sekarang. def chickStep(self):
for i in self.chicks:
ci = self.cs[i]
ci.x += 2*random()*(self.cs[ci.hen].x-ci.x)
Pada ketika ini, rangka kerja algoritma kelompok telah berjaya dibina Seterusnya, bahagian paling kritikal, pengoptimuman, akan dilaksanakan. 其基本逻辑是,输入一个待优化func,通过将每只鸡的位置x带入到这个函数中,得到一个判定值,最后通过这个判定值,来不断更新鸡群。 除了这个函数之外,还需要输入一些其他参数,比如整个鸡群算法的迭代次数,以及鸡群更新的频次等等 其中,printBest可以将当前最佳结果打印出来,其形式为 算法完成之后,当然要找个函数测试一下,测试函数为# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self, func, N, T, msgT):
for n in range(N):
# 计算优化参数
for c in self.cs:
c.best = func(c.x)
# 分别更新公鸡、母鸡和小鸡
self.cockStep()
self.henStep()
self.chickStep()
if (n+1)%T == 0:
self.update() #每T次更新一次种群
self.printBest(n)
self.printBest(n)def printBest(self,n):
fitness = [c.best for c in self.cs]
best = np.min(fitness)
ind = np.where(fitness==best)[0]
msg = f"已经迭代{n}次,最佳优化结果为{np.min(fitness)},参数为:\n"
msg += ", ".join([f"{x:.6f}" for x in self.cs[ind].x])
print(msg)测试
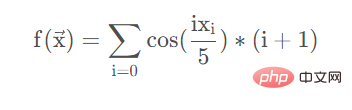
def test(xs):
_sum = 0.0
for i in range(len(xs)):
_sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
return _sum
if __name__ == "__main__":
cNum = [15,20,100]
s = Swarm(cNum, 5, (-5,5))
s.optimize(test, 20, 5)
测试结果如下
已经迭代4次,最佳优化结果为-5.793762423022024,参数为:
-6.599526, 3.117137, 5.959538, 7.225785, 5.204990
已经迭代9次,最佳优化结果为-10.61594651972434,参数为:
-7.003724, -5.589730, 0.981409, 12.920325, -19.006112
已经迭代14次,最佳优化结果为-9.143596747975293,参数为:
5.388234, -3.714421, -5.254391, -5.216215, -6.079223
已经迭代19次,最佳优化结果为-11.097888385616995,参数为:
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
已经迭代19次,最佳优化结果为-11.097888385616995,参数为:
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan algoritma kawanan ayam dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




