
(1) Matriks identiti
ialah matriks segi empat sama di mana elemen pada pepenjuru utama adalah kesemuanya 1 dan elemen yang selebihnya adalah 0 .
Dalam NumPy, anda boleh menggunakan fungsi mata untuk mencipta tatasusunan dua dimensi tersebut. Kita hanya perlu memberikan parameter untuk menentukan bilangan 1 elemen dalam matriks.
Contohnya, buat tatasusunan 3×3:
import numpy as np I2 = np.eye(3) print(I2) [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
(2) Gunakan fungsi savetxt untuk menyimpan data ke dalam fail Sudah tentu, kita perlu menentukan nama fail dan array untuk disimpan.
np.savetxt('eye.txt', I2)#创建一个eye.txt文件,用于保存I2的数据
Format CSV (Comma-Separated Value) ialah format fail biasa, fail dump pangkalan data Ia dalam format CSV , dan setiap medan dalam fail sepadan dengan lajur dalam jadual pangkalan data perisian hamparan (seperti Microsoft Excel) boleh memproses fail CSV.
nota: Fungsi loadtxt dalam NumPy boleh membaca fail CSV dengan mudah, membahagikan medan secara automatik dan memuatkan data ke dalam tatasusunan NumPy
Kandungan data data.csv:
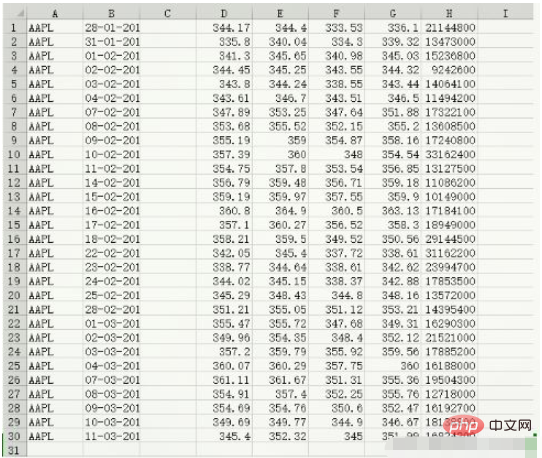
c, v = np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True) # usecols的参数为一个元组,以获取第7字段至第8字段的数据 # unpack参数设置为True,意思是分拆存储不同列的数据,即分别将收盘价和成交量的数组赋值给变量c和v print(c) [336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16 354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62 342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76 352.47 346.67 351.99] print(v) [21144800. 13473000. 15236800. 9242600. 14064100. 11494200. 17322100. 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100. 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400. 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700. 18138800. 16824200.] print(type(c)) print(type(v)) <class 'numpy.ndarray'> <class 'numpy.ndarray'>
VWAP Overview: VWAP (Volume- Weighted Average Price (Volume Weighted Price) Harga Purata) ialah kuantiti ekonomi yang sangat penting, yang mewakili harga "purata" aset kewangan.
Semakin tinggi volum harga tertentu, semakin besar berat harga tersebut.
VWAP ialah purata wajaran yang dikira dengan volum dagangan sebagai berat, dan sering digunakan dalam perdagangan algoritma.
vwap = np.average(c,weights=v) print('成交量加权平均价格vwap =', vwap) 成交量加权平均价格vwap = 350.5895493532009
Fungsi min dalam NumPy boleh mengira min aritmetik unsur tatasusunan
print('c数组中元素的算数平均值为: {}'.format(np.mean(c)))
c数组中元素的算数平均值为: 351.0376666666667Ikhtisar TWAP:
Dalam bidang ekonomi, TWAP (Harga Purata Wajaran Masa, harga purata wajaran masa) ialah satu lagi " Harga purata penunjuk. Sekarang kita telah mengira VWAP, mari kita mengira TWAP juga. Sebenarnya, TWAP hanyalah satu varian Idea asasnya ialah harga terkini adalah lebih penting, jadi kita harus memberikan wajaran yang lebih tinggi kepada harga terkini. Kaedah paling mudah ialah menggunakan fungsi arange untuk mencipta urutan nombor asli yang bermula dari 0 dan meningkat secara berurutan. Bilangan nombor asli ialah bilangan harga penutup. Sudah tentu, ini tidak semestinya cara yang betul untuk mengira TWAP.
t = np.arange(len(c)) print('时间加权平均价格twap=', np.average(c, weights=t)) 时间加权平均价格twap= 352.4283218390804
h, l = np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True)
print('h数据为: \n{}'.format(h))
print('-'*10)
print('l数据为: \n{}'.format(l))
h数据为:
[344.4 340.04 345.65 345.25 344.24 346.7 353.25 355.52 359. 360.
357.8 359.48 359.97 364.9 360.27 359.5 345.4 344.64 345.15 348.43
355.05 355.72 354.35 359.79 360.29 361.67 357.4 354.76 349.77 352.32]
----------
l数据为:
[333.53 334.3 340.98 343.55 338.55 343.51 347.64 352.15 354.87 348.
353.54 356.71 357.55 360.5 356.52 349.52 337.72 338.61 338.37 344.8
351.12 347.68 348.4 355.92 357.75 351.31 352.25 350.6 344.9 345. ]
print('h数据的最大值为: {}'.format(np.max(h)))
print('l数据的最小值为: {}'.format(np.min(l)))
h数据的最大值为: 364.9
l数据的最小值为: 333.53
NumPy中有一个ptp函数可以计算数组的取值范围
该函数返回的是数组元素的最大值和最小值之间的差值
也就是说,返回值等于max(array) - min(array)
print('h数据的最大值-最小值的差值为: \n{}'.format(np.ptp(h)))
print('l数据的最大值-最小值的差值为: \n{}'.format(np.ptp(l)))
h数据的最大值-最小值的差值为:
24.859999999999957
l数据的最大值-最小值的差值为:
26.970000000000027Median: Kami boleh menggunakan Beberapa ambang adalah. digunakan untuk membuang outlier, tetapi ada cara yang lebih baik, iaitu median.
Susun nilai pembolehubah mengikut saiz untuk membentuk jujukan Nombor di tengah jujukan ialah median.
Sebagai contoh, jika kita mempunyai 5 nilai 1, 2, 3, 4, dan 5, maka median ialah nombor tengah 3.
m = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
print('m数据中的中位数为: {}'.format(np.median(m)))
m数据中的中位数为: 352.055
# 数组排序后,查找中位数
sorted_m = np.msort(m)
print('m数据排序: \n{}'.format(sorted_m))
N = len(c)
print('m数据中的中位数为: {}'.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2))
m数据排序:
[336.1 338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5 346.67
348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2
355.36 355.76 356.85 358.16 358.3 359.18 359.56 359.9 360. 363.13]
m数据中的中位数为: 352.055
方差:
方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。
print('variance =', np.var(m))
variance = 50.126517888888884
var_hand = np.mean((m-m.mean())**2)
print('var =', var_hand)
var = 50.126517888888884Nota: Perbezaan dalam pengiraan antara varians sampel dan varians populasi. Varians populasi ialah jumlah kuasa dua sisihan dibahagikan dengan bilangan data, manakala varians sampel ialah jumlah kuasa dua sisihan dibahagikan dengan bilangan data sampel tolak 1, di mana bilangan data sampel tolak 1 (iaitu n- 1) dipanggil darjah kebebasan. Sebab perbezaan ini adalah untuk memastikan varians sampel adalah penganggar yang tidak berat sebelah.
Dalam literatur akademik, analisis harga penutup selalunya berdasarkan pulangan saham dan pulangan logaritma.
Kadar pulangan mudah merujuk kepada kadar perubahan antara dua harga bersebelahan, manakala kadar pulangan logaritma merujuk kepada perbezaan antara kedua-duanya selepas mengambil logaritma semua harga.
Kami belajar tentang logaritma di sekolah menengah Logaritma "a" tolak logaritma "b" adalah sama dengan logaritma "a dibahagikan dengan b". Oleh itu, pulangan log juga boleh digunakan untuk mengukur kadar perubahan harga.
Perhatikan bahawa memandangkan kadar pulangan ialah nisbah, contohnya kita membahagikan dolar AS dengan dolar AS (ia juga boleh menjadi unit mata wang lain), ia tidak berdimensi.
Ringkasnya, perkara yang paling diminati pelabur ialah varians atau sisihan piawai pulangan, kerana ia mewakili saiz risiko pelaburan.
(1) Mula-mula, mari kita hitung kadar pulangan mudah. Fungsi diff dalam NumPy boleh mengembalikan tatasusunan yang terdiri daripada perbezaan antara elemen tatasusunan bersebelahan. Ini agak serupa dengan kalkulus pembezaan. Untuk mengira hasil, kita juga perlu membahagikan harga hari sebelumnya dengan perbezaan. Walau bagaimanapun, perlu diperhatikan di sini bahawa tatasusunan yang dikembalikan oleh perbezaan mempunyai satu elemen kurang daripada tatasusunan harga penutupan. returns = np.diff(arr)/arr[:-1]
Perhatikan bahawa kami tidak membahagikan dengan nilai terakhir dalam tatasusunan harga penutup. Seterusnya, gunakan fungsi std untuk mengira sisihan piawai:
print ("Standard deviation =", np.std(returns))(2) Pulangan log adalah lebih mudah untuk dikira. Kami mula-mula menggunakan fungsi log untuk mendapatkan logaritma setiap harga penutup, dan kemudian menggunakan fungsi diff pada hasilnya.
logreturns = np.diff( np.log(c) )
Secara amnya, kita harus menyemak tatasusunan input untuk memastikan ia tidak mengandungi sifar dan nombor negatif. Jika tidak, anda akan mendapat mesej ralat. Walau bagaimanapun, dalam contoh kami, harga saham sentiasa positif, jadi cek boleh ditinggalkan.
(3) Kami berkemungkinan sangat berminat dengan hari dagangan yang mempunyai pulangan positif.
Selepas melengkapkan langkah sebelumnya, kita hanya perlu menggunakan fungsi where untuk melakukan ini. Fungsi where boleh mengembalikan nilai indeks semua elemen tatasusunan yang memenuhi syarat yang ditentukan.
Masukkan kod berikut:
posretindices = np.where(returns > 0) print "Indices with positive returns", posretindices 即可输出该数组中所有正值元素的索引。 Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)
(4) 在投资学中,波动率(volatility)是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率(如年波动率或月波动率)时,需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值,再除以交易日倒数的平方根,通常交易日取252天。用std和mean函数来计算
代码如下所示:
annual_volatility = np.std(logreturns)/np.mean(logreturns) annual_volatility = annual_volatility / np.sqrt(1./252.)
(5) sqrt函数中的除法运算。在Python中,整数的除法和浮点数的除法运算机制不同(python3已修改该功能),我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似,计算月波动率如下:
annual_volatility * np.sqrt(1./12.)
c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
returns = np.diff(c)/c[:-1]
print('returns的标准差: {}'.format(np.std(returns)))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns>0)
print('retruns中元素为正数的位置: \n{}'.format(posretindices))
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility/np.sqrt(1/252)
print('每年波动率: {}'.format(annual_volatility))
print('每月波动率:{}'.format(annual_volatility*np.sqrt(1/12)))
returns的标准差: 0.012922134436826306
retruns中元素为正数的位置:
(array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
25, 28], dtype=int64),)
每年波动率: 129.27478991115132
每月波动率:37.318417377317765Atas ialah kandungan terperinci Cara menggunakan NumPy dalam fungsi biasa Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




