Cara menggunakan senarai bersebelahan untuk menyimpan graf di Jawa
1. Sentuhan penamat
Senarai bersebelahan ialah kaedah penyimpanan berantai untuk graf struktur datanya terdiri daripada dua bahagian: nod dan titik bersebelahan.
Senarai bersebelahan boleh digunakan untuk mewakili graf tidak terarah, graf terarah dan rangkaian. Ini dijelaskan menggunakan graf tidak berarah.
1. Graf tidak berarah
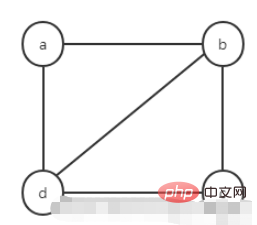
2 Jadual terpaut graf tidak berarah
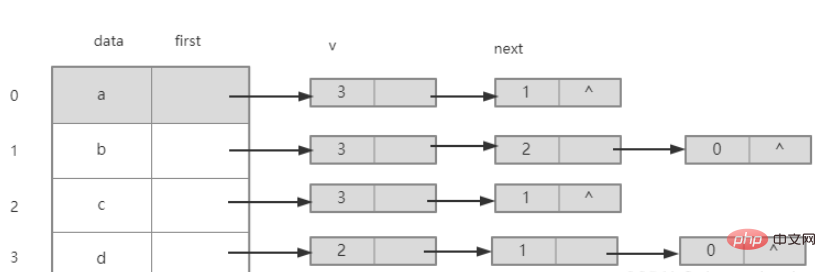
3 .Penjelasan
Titik bersebelahan nod a ialah nod b dan d, dan indeks storan bagi titik bersebelahannya ialah 1 dan 3. Letakkannya ke dalam senarai berpaut tunggal di belakang nod a mengikut kaedah sisipan kepala (urutan terbalik ).
Titik bersebelahan nod b ialah nod a, c, dan d Indeks storan bagi titik bersebelahannya ialah 0, 2, dan 3. Letakkannya ke dalam senarai terpaut tunggal di belakang nod b mengikut kepala. kaedah sisipan (tertib terbalik).
Titik bersebelahan nod c ialah nod b dan d, dan indeks storan bagi titik bersebelahannya ialah 1 dan 3. Ia dimasukkan ke dalam senarai berpaut tunggal di belakang nod c mengikut kaedah interpolasi kepala (terbalik pesanan).
Titik bersebelahan nod d ialah nod a, b, c Subskrip storan titik bersebelahannya ialah 0, 1, 2. Mengikut kaedah interpolasi kepala (tertib terbalik), masukkannya ke dalam satuan. senarai terpaut di belakang nod d tengah.
4. Ciri-ciri senarai bersebelahan graf tidak berarah
adalah seperti berikut Jika terdapat n nod dan tepi dalam graf tidak berarah, maka terdapat n nod dalam jadual nod dan. 2e dalam jadual nod jiran.
Dasar nod ialah bilangan nod dalam senarai terpaut tunggal di belakang nod.
2. Struktur data senarai bersebelahan
1 Nod
termasuk data maklumat nod dan penunjuk ke titik bersebelahan pertama.

2 Titik bersebelahan
termasuk subskrip storan v titik bersebelahan dan penunjuk ke titik bersebelahan seterusnya, jika ia bersebelahan titik rangkaian , maka domain berat w perlu ditambah, seperti yang ditunjukkan dalam rajah di bawah.
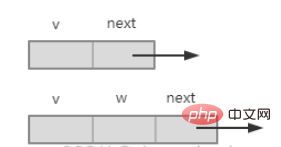
3. Langkah-langkah algoritma
1 Masukkan bilangan nod dan tepi.
2 Masukkan maklumat nod secara bergilir-gilir, simpannya dalam medan data tatasusunan nod Vex[] dan biarkan medan pertama Vex[] kosong.
3 Masukkan dua nod yang dipasang pada setiap tepi secara bergilir-gilir Jika ia adalah rangkaian, anda juga perlu memasukkan berat tepi.
Jika ia adalah graf tidak terarah, masukkan a b, pertanyaan nod a, b, simpan subskrip i, j dalam tatasusunan nod Vex[], buat titik bersebelahan baharu s, biarkan s.v = j;s . next=null;Kemudian masukkan nod s sebelum titik bersebelahan pertama nod ke-i (kaedah interpolasi kepala). Dalam graf tidak berarah, terdapat tepi dari nod a ke nod b, dan terdapat tepi dari nod b ke nod a, jadi titik bersebelahan baharu s2 perlu dibuat, biarkan s2.v = i;s2.next= null; dan kemudian biarkan Nod s2 dimasukkan sebelum titik bersebelahan pertama nod ke-j (kaedah interpolasi kepala).
Jika ia adalah graf tidak terarah, masukkan a b, pertanyaan nod a, b, simpan subskrip i, j dalam tatasusunan nod Vex[], buat titik bersebelahan baharu s, biarkan s.v = j;s . next=null;Kemudian masukkan nod s sebelum titik bersebelahan pertama nod ke-i (kaedah interpolasi kepala).
Jika ia merupakan rangkaian tidak terarah atau rangkaian terarah, ia diproses dengan cara yang sama seperti graf tidak terarah atau graf terarah, kecuali nod bersebelahan mempunyai domain berat tambahan.
4. Perlaksanaan
package graph;
import java.util.Scanner;
public class CreateALGraph {
static final int MaxVnum = 100; // 顶点数最大值
public static void main(String[] args) {
ALGraph G = new ALGraph();
for (int i = 0; i < G.Vex.length; i++) {
G.Vex[i] = new VexNode();
}
CreateALGraph(G); // 创建有向图邻接表
printg(G); // 输出邻接表
}
static int locatevex(ALGraph G, char x) {
for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
if (x == G.Vex[i].data)
return i;
return -1; // 没找到
}
// 插入一条边
static void insertedge(ALGraph G, int i, int j) {
AdjNode s = new AdjNode();
s.v = j;
s.next = G.Vex[i].first;
G.Vex[i].first = s;
}
// 输出邻接表
static void printg(ALGraph G) {
System.out.println("----------邻接表如下:----------");
for (int i = 0; i < G.vexnum; i++) {
AdjNode t = G.Vex[i].first;
System.out.print(G.Vex[i].data + ": ");
while (t != null) {
System.out.print("[" + t.v + "]\t");
t = t.next;
}
System.out.println();
}
}
// 创建有向图邻接表
static void CreateALGraph(ALGraph G) {
int i, j;
char u, v;
System.out.println("请输入顶点数和边数:");
Scanner scanner = new Scanner(System.in);
G.vexnum = scanner.nextInt();
G.edgenum = scanner.nextInt();
System.out.println("请输入顶点信息:");
for (i = 0; i < G.vexnum; i++)//输入顶点信息,存入顶点信息数组
G.Vex[i].data = scanner.next().charAt(0);
for (i = 0; i < G.vexnum; i++)
G.Vex[i].first = null;
System.out.println("请依次输入每条边的两个顶点u,v");
while (G.edgenum-- > 0) {
u = scanner.next().charAt(0);
v = scanner.next().charAt(0);
i = locatevex(G, u); // 查找顶点 u 的存储下标
j = locatevex(G, v); // 查找顶点 v 的存储下标
if (i != -1 && j != -1)
insertedge(G, i, j);
else {
System.out.println("输入顶点信息错!请重新输入!");
G.edgenum++; // 本次输入不算
}
}
}
}
// 定义邻接点类型
class AdjNode {
int v; // 邻接点下标
AdjNode next; // 指向下一个邻接点
}
// 定义顶点类型
class VexNode {
char data; // VexType为顶点的数据类型,根据需要定义
AdjNode first; // 指向第一个邻接点
}
// 定义邻接表类型
class ALGraph {
VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
int vexnum; // 顶点数
int edgenum; // 边数
}5.
Atas ialah kandungan terperinci Cara menggunakan senarai bersebelahan untuk menyimpan graf di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Sempurna di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan Nombor Sempurna di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor Perfect dalam Java?, contoh dengan pelaksanaan kod.
 Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Weka di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Weka di Jawa. Di sini kita membincangkan Pengenalan, cara menggunakan weka java, jenis platform, dan kelebihan dengan contoh.
 Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Nombor Smith di Jawa
Aug 30, 2024 pm 04:28 PM
Panduan untuk Nombor Smith di Jawa. Di sini kita membincangkan Definisi, Bagaimana untuk menyemak nombor smith di Jawa? contoh dengan pelaksanaan kod.
 Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Soalan Temuduga Java Spring
Aug 30, 2024 pm 04:29 PM
Dalam artikel ini, kami telah menyimpan Soalan Temuduga Spring Java yang paling banyak ditanya dengan jawapan terperinci mereka. Supaya anda boleh memecahkan temuduga.
 Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Cuti atau kembali dari Java 8 Stream Foreach?
Feb 07, 2025 pm 12:09 PM
Java 8 memperkenalkan API Stream, menyediakan cara yang kuat dan ekspresif untuk memproses koleksi data. Walau bagaimanapun, soalan biasa apabila menggunakan aliran adalah: bagaimana untuk memecahkan atau kembali dari operasi foreach? Gelung tradisional membolehkan gangguan awal atau pulangan, tetapi kaedah Foreach Stream tidak menyokong secara langsung kaedah ini. Artikel ini akan menerangkan sebab -sebab dan meneroka kaedah alternatif untuk melaksanakan penamatan pramatang dalam sistem pemprosesan aliran. Bacaan Lanjut: Penambahbaikan API Java Stream Memahami aliran aliran Kaedah Foreach adalah operasi terminal yang melakukan satu operasi pada setiap elemen dalam aliran. Niat reka bentuknya adalah
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Panduan untuk TimeStamp to Date di Java. Di sini kita juga membincangkan pengenalan dan cara menukar cap waktu kepada tarikh dalam java bersama-sama dengan contoh.
 Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Program Java untuk mencari kelantangan kapsul
Feb 07, 2025 am 11:37 AM
Kapsul adalah angka geometri tiga dimensi, terdiri daripada silinder dan hemisfera di kedua-dua hujungnya. Jumlah kapsul boleh dikira dengan menambahkan isipadu silinder dan jumlah hemisfera di kedua -dua hujungnya. Tutorial ini akan membincangkan cara mengira jumlah kapsul yang diberikan dalam Java menggunakan kaedah yang berbeza. Formula volum kapsul Formula untuk jumlah kapsul adalah seperti berikut: Kelantangan kapsul = isipadu isipadu silinder Dua jumlah hemisfera dalam, R: Radius hemisfera. H: Ketinggian silinder (tidak termasuk hemisfera). Contoh 1 masukkan Jejari = 5 unit Ketinggian = 10 unit Output Jilid = 1570.8 Unit padu menjelaskan Kirakan kelantangan menggunakan formula: Kelantangan = π × r2 × h (4
 PHP vs Python: Memahami Perbezaan
Apr 11, 2025 am 12:15 AM
PHP vs Python: Memahami Perbezaan
Apr 11, 2025 am 12:15 AM
PHP dan Python masing -masing mempunyai kelebihan sendiri, dan pilihannya harus berdasarkan keperluan projek. 1.Php sesuai untuk pembangunan web, dengan sintaks mudah dan kecekapan pelaksanaan yang tinggi. 2. Python sesuai untuk sains data dan pembelajaran mesin, dengan sintaks ringkas dan perpustakaan yang kaya.






