
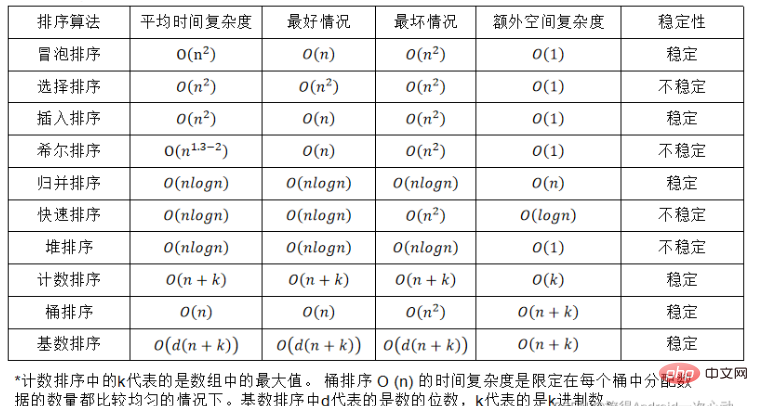
Anggapkan terdapat berbilang rekod dengan kata kunci yang sama dalam urutan rekod yang akan diisih, rekod ini dijamin menjadi Susunan relatif rekod kekal tidak berubah, iaitu, dalam urutan asal, a[i]=a[j], dan a[i] sebelum a[j], adalah dijamin bahawa a[i] masih sebelum a[j]. Algoritma pengisihan ini dipanggil stabil;
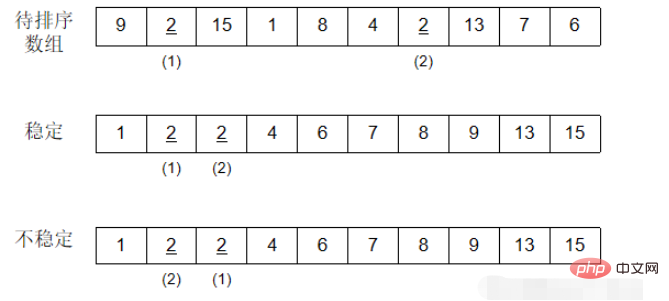
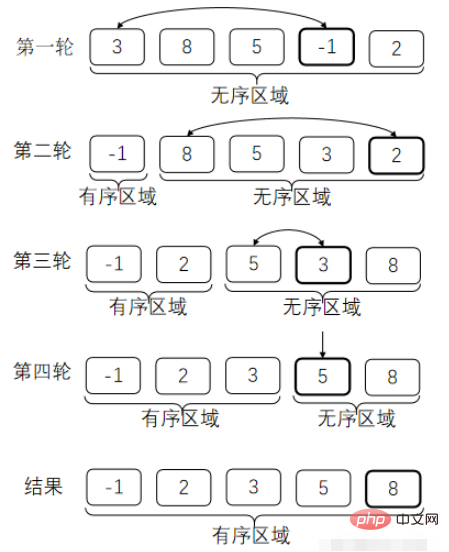
Pilih elemen terkecil daripada elemen yang hendak diisih setiap kali, dan letakkan dalam urutan dengan yang pertama, ke-2, ke-3. ... unsur ditukar. Ini membentuk kawasan tertib di hadapan tatasusunan. Setiap kali pertukaran dilakukan, panjang kawasan yang dipesan ditambah satu.
public static void selectionSort(int[] arr){
//细节一:这里可以是arr.length也可以是arr.length-1
for (int i = 0; i < arr.length-1 ; i++) {
int mini = i;
for (int j = i+1; j < arr.length; j++) {
//切换条件,决定升序还是降序
if(arr[mini]>arr[j]) mini =j;
}
swap(arr,mini,i);
}
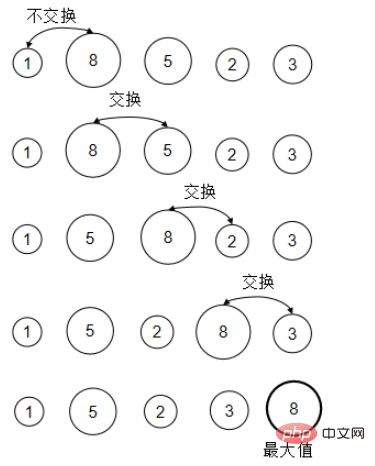
}Bandingkan dua nombor bersebelahan secara bergilir-gilir, dan tukarkannya jika dalam susunan yang salah dengan cara ini, setiap Selepas pusingan perbandingan, anda boleh meletakkan nombor terbesar di tempat yang sepatutnya. (Ia seperti membawa gelembung terbesar ke atas)
Di sini kami menerangkan maksud susunan yang salah. Kami mengisih dalam tertib menaik Nilai kemudian harus lebih besar daripada atau sama dengan nilai sebelumnya.
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
//记录本次有没有进行交换的操作
boolean flag = false;
//保存在头就动头,保存在尾就动尾
for(int j =0 ; j < arr.length-1-i ; j++){
//升序降序选择地
if(arr[j] > arr[j+1])
{
swap(arr,j,j+1);
flag = true;
}
}
//如果本次没有进行交换操作,表示数据已经有序
if(!flag){break;} //程序结束
}
}Isih sisipan sebenarnya boleh difahami sebagai proses melukis kad apabila kita bermain poker. dan setiap kali kad disentuh, kad itu dimasukkan ke tempat yang sepatutnya. Selepas semua kad disentuh, semua kad akan teratur.
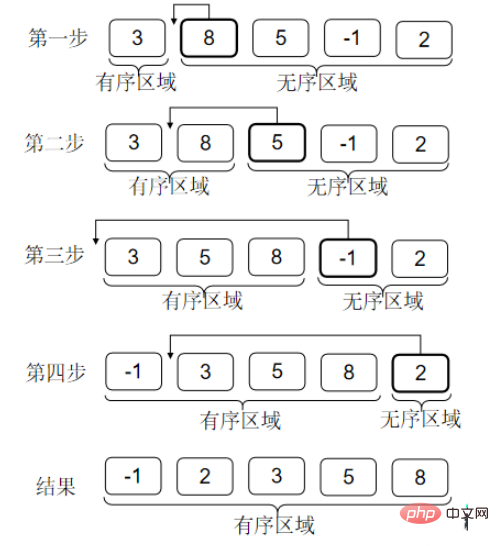
Berfikir: Satu kawasan tertib terbentuk di hadapan tatasusunan Kemudian apabila saya mencari kedudukan di mana nombor semasa perlu dimasukkan, saya menggunakan pembahagian binari mengurangkan kerumitan jenis sisipan Adakah ia telah dioptimumkan kepada O(nlogn)?
Membahagikan kepada dua bahagian boleh mencari kedudukan dengan kerumitan log. Perkara utama ialah jika anda menggunakan tatasusunan untuk menyimpan data, kerumitan mengalihkan semula data semasa pemasukan masih O(n). Jika anda menggunakan senarai terpaut, mencari kedudukan dan memasukkannya ialah O(1), tetapi senarai terpaut tidak boleh dibahagikan kepada dua.
public static void insertSort(int[] arr){
//从第二个数开始,把每个数依次插入到指定的位置
for(int i = 1 ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-1;
//大的后移操作
while(j >= 0 && arr[j] > key)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}Isih bukit ialah algoritma pengisihan yang dicadangkan oleh Donald Shell pada tahun 1959. Ia merupakan versi pengisihan sisipan langsung yang lebih baik dan cekap. Pengisihan bukit memerlukan penyediaan set data sebagai jujukan tambahan.
Set data ini perlu memenuhi tiga syarat berikut:
1 Data disusun dalam tertib menurun
2 panjang tatasusunan yang hendak diisih
3. Nilai minimum dalam data ialah 1.
Selagi tatasusunan memenuhi keperluan di atas, ia boleh digunakan sebagai jujukan tambahan, tetapi jujukan tambahan yang berbeza akan menjejaskan kecekapan pengisihan. Di sini kami menggunakan {5,3,1} sebagai jujukan tambahan untuk menerangkan
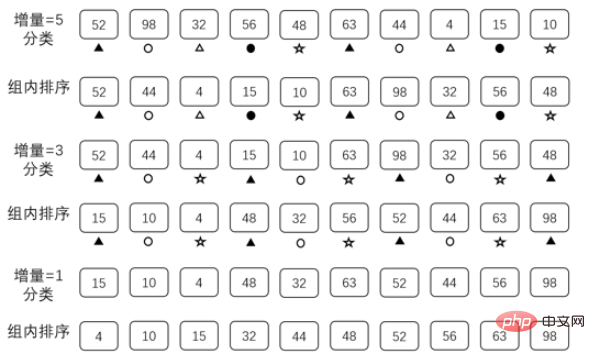
Sebab pengoptimuman: mengurangkan jumlah data, menjadikan O(n) dan O( n Perbezaan antara ^2) tidak besar
public static void shellSort(int[] arr){
//分块处理
int gap = arr.length/2; //增量
while(1<=gap)
{
//插入排序:只不过是与增量位交换
for(int i = gap ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-gap;
while(j >= 0 && arr[j] > key)
{
arr[j+gap] = arr[j];
j-=gap;
}
arr[j+gap] = key;
}
gap = gap/2;
}
}ialah pokok binari lengkap, terbahagi kepada dua jenis: timbunan akar besar dan timbunan akar kecil
boleh O( 1) Ambil nilai maksimum/minimum, padamkan nilai maksimum/minimum dalam O(logn), dan masukkan elemen dalam O(logn)
MIN-HEAPIFY (i) Operasi:
Kami menganggap pokok binari lengkap Kedua-dua subpokok kiri dan subpokok kanan nod tertentu i memenuhi sifat timbunan akar kecil Andaikan bahawa anak kiri nod i adalah left_i, dan anak kanan nod saya adalah rigℎt_i. Jika a[i] lebih besar daripada a[left_i] atau a[rigℎt_i], maka keseluruhan subpokok dengan nod i sebagai nod akar tidak memenuhi sifat timbunan akar kecil Kita kini perlu melakukan operasi: put i sebagai nod akar Subpohon nod akar dilaraskan menjadi timbunan akar kecil.
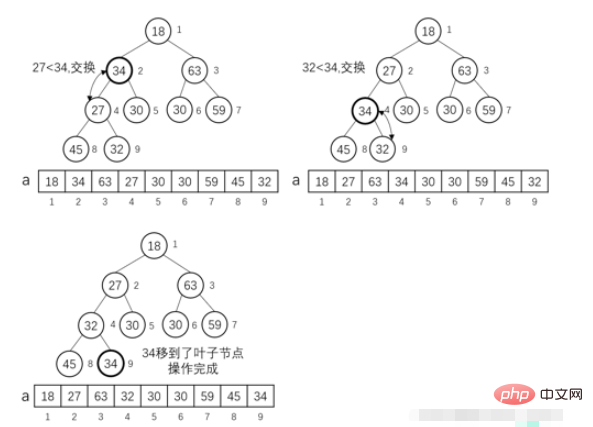
//堆排序
public static void heapSort(int[] arr){
//开始调整的位置为最后一个叶子节点
int start = (arr.length - 1)/2;
//从最后一个叶子节点开始遍历,调整二叉树
for (int i = start; i >= 0 ; i--){
maxHeap(arr, arr.length, i);
}
for (int i = arr.length - 1; i > 0; i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
//将二叉树调整为大顶堆
public static void maxHeap(int[] arr, int size, int index){
//建立左子节点
int leftNode = 2 * index + 1;
//建立右子节点
int rightNode = 2 * index + 2;
int maxNode = index;
//左子节点的值大于根节点时调整
if (leftNode < size && arr[leftNode] > arr[maxNode]){
maxNode = leftNode;
}
//右子节点的值大于根节点时调整
if (rightNode < size && arr[rightNode] > arr[maxNode]){
maxNode = rightNode;
}
if (maxNode != index){
int temp = arr[maxNode];
arr[maxNode] = arr[index];
arr[index] = temp;
//交换之后可能会破坏原来的结构,需要再次调整
//递归调用进行调整
maxHeap(arr, size, maxNode);
}
}Saya menggunakan timbunan akar yang besar Proses pengisihan bermula kepada: pertama akar kiri dan kemudian akar kanan (bergantung pada cara anda menulisnya) -> Setiap akar Atas turun. (Kiri, kanan, atas dan bawah)
Merge sort ialah aplikasi biasa bagi kaedah bahagi dan takluk kaedah penaklukan adalah untuk membahagikan masalah kompleks kepada dua atau lebih sub-masalah yang serupa atau serupa, dan kemudian membahagikan sub-masalah kepada sub-masalah yang lebih kecil...sehingga sub-masalah terakhir cukup kecil untuk diselesaikan secara langsung, dan kemudian menggabungkan penyelesaian kepada sub-masalah untuk mendapatkan penyelesaian kepada masalah asal .
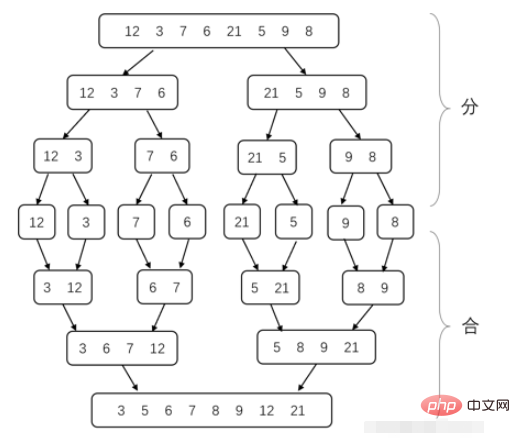
Proses mencantumkan sub-masalah penguraian isihan adalah untuk membahagi tatasusunan kepada 2 bahagian setiap kali sehingga panjang tatasusunan ialah 1 (kerana tatasusunan dengan hanya satu nombor dipesan) . Kemudian gabungkan tatasusunan tertib bersebelahan menjadi satu tatasusunan tertib. Sehingga kesemuanya disatukan, keseluruhan tatasusunan diisih. Masalah yang perlu diselesaikan sekarang ialah bagaimana untuk menggabungkan dua tatasusunan tertib menjadi satu tatasusunan tertib. Malah, setiap kali dua elemen terkecil daripada dua tatasusunan dibandingkan, yang mana lebih kecil dipilih
| <🎜>Array b<🎜> | <🎜>Penerangan<🎜> | <🎜>Anasunan jawapan<🎜> | ||||||||||||||||||||||||||||
| <🎜>2,5,7<🎜> | <🎜>1,3,4<🎜> | <🎜>1<2, ambil 1. Penunjuk tatasusunan b digerakkan ke belakang <🎜> | <🎜>1<🎜> | ||||||||||||||||||||||||||||
| <🎜>2,5,7 <🎜> | <🎜>1,3,4<🎜> | <🎜>2<3, ambil 2 dan gerakkan penunjuk tatasusunan ke belakang<🎜>< /td> | <🎜>1,2<🎜> | ||||||||||||||||||||||||||||
| <🎜>2,5,7<🎜> | <🎜> 1,3,4 <🎜> | <🎜>3<5, ambil 3 dan gerakkan penunjuk tatasusunan b ke belakang<🎜> | <🎜>1,2, 3<🎜> | ||||||||||||||||||||||||||||
| <🎜>2,5,7<🎜> | <🎜>1,3,4<🎜> | <🎜> 4<5, ambil 4 dan gerakkan penunjuk tatasusunan b ke belakang<🎜> | <🎜>1,2,3,4<🎜> | < /tr>||||||||||||||||||||||||||||
| <🎜>2,5,7<🎜> | <🎜>1,3,4<🎜> | <🎜>Terdapat tiada unsur dalam tatasusunan b, ambil 5<🎜 > | <🎜>1,2,3,4,5<🎜> | ||||||||||||||||||||||||||||
| <🎜> 2,5,7<🎜> | <🎜>1,3,4<🎜> | <🎜>Tiada unsur dalam tatasusunan b, ambil 7<🎜>< /td> | <🎜>1, 2,3,4,5,7<🎜> |
public static void mergeSort(int[] arr, int low, int high){
int middle = (high + low)/2;
if (low < high){
//递归排序左边
mergeSort(arr, low, middle);
//递归排序右边
mergeSort(arr, middle +1, high);
//将递归排序好的左右两边合并
merge(arr, low, middle, high);
}
}
public static void merge(int[] arr, int low, int middle, int high){
//存储归并后的临时数组
int[] temp = new int[high - low + 1];
int i = low;
int j = middle + 1;
//记录临时数组中存放数字的下标
int index = 0;
while (i <= middle && j <= high){
if (arr[i] < arr[j]){
temp[index] = arr[i];
i++;
} else {
temp[index] = arr[j];
j++;
}
index++;
}
//处理剩下的数据
while (j <= high){
temp[index] = arr[j];
j++;
index++;
}
while (i <= middle){
temp[index] = arr[i];
i++;
index++;
}
//将临时数组中的数据放回原来的数组
for (int k = 0; k < temp.length; ++k){
arr[k + low] = temp[k];
}
}快速排序的工作原理是:从待排序数组中随便挑选一个数字作为基准数,把所有比它小的数字放在它的左边,所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。
全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边,所有比基准数大的数字放在它的右边。这个操作,我们称为“划分”(Partition)。

//快速排序
public static void QuickSort1(int[] arr, int start, int end){
int low = start, high = end;
int temp;
if(start < end){
int guard = arr[start];
while(low != high){
while(high > low && arr[high] >= guard) high--;
while(low < high && arr[low] <= guard) low++;
if(low < high){
temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
}
arr[start] = arr[low];
arr[low] = guard;
QuickSort1(arr, start, low-1);
QuickSort1(arr, low+1, end);
}
}
//快速排序改进版(填坑法)
public static void QuickSort2(int[] arr, int start, int end){
int low = start, high = end;
if(start < end){
while(low != high){
int guard = arr[start];//哨兵元素
while(high > low && arr[high] >= guard) high--;
arr[low] = arr[high];
while(low < high && arr[low] <= guard) low++;
arr[high] = arr[low];
}
arr[low] = guard;
QuickSort2(arr, start, low-1);
QuickSort2(arr, low+1, end);
}
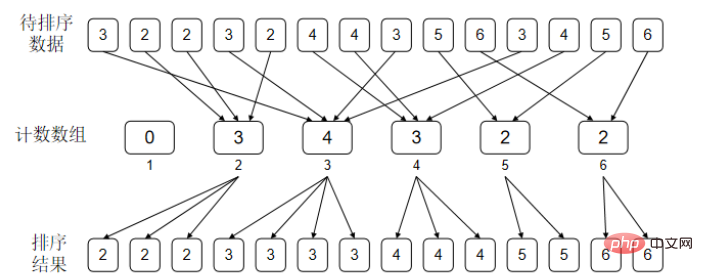
}计算一下每一个数出现了多少次。举一个例子,比如待排序的数据中1出现了2次,2出现了0次,3出现了3次,4出现了1次,那么排好序的结果就是{1.1.3.3.3.4}。
//鸽巢排序
public static void PigeonholeSort(int[] arr){
//获取最大值
int k = 0;
for (int i = 0; i < arr.length; i++) {
k = Math.max(k,arr[i]);
}
//创建计数数组并且初始化为0
int[] cnt = new int[k+10];
for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
int j = 0;
for(int i = 0 ; i <=k ; i++)
{
while(cnt[i]!=0)
{
arr[j]=i;
j++;
cnt[i]--;
}
}
}鸽巢排序其实算不上是真正意义上的排序算法,它的局限性很大。只能对纯整数数组进行排序,举个例子,如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。
先考虑这样一个事情:如果对于待排序数据中的任意一个元素 a[i],我们知道有 m 个元素比它小,那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢?(这里先假设数据中没有相等的元素)。计数排序主要就是依赖这个原理来实现的。
比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2} 0,1,2,3,4
此时cnt[i]表示数据i出现了多少次,
然后对cnt数组做一个前缀和{1,1,3,3,5} :0,1,2,3,4
此时cnt[i]表示数据中小于等于i的数字有多少个
待排序数组 | 计数数组 | 说明 | 答案数组ans |
2,4,0,2,4 | 1,1,3,3,5 | 初始状态 | null,null,null,null,null, |
2,4,0,2,4 | 1,1,3,3,5 | cnt[4]=5,ans第5位赋值,cnt[4]-=1 | null,null,null,null,4 |
2,4,0,2,4 | 1,1,3,3,4 | cnt[2]=3,ans第3位赋值,cnt[2]-=1 | null,null,2 null,4 |
2,4,0,2,4 | 1,1,2,3,4 | cnt[0]=1,ans第1位赋值,cnt[0]-=1 | 0,null,2,null,4 |
2,4,0,2,4 | 0,1,2,3,4 | cnt[4]=4,ans第4位赋值,cnt[4]-=1 | 0,null,2,4,4 |
2,4,0,2,4 | 0,1,2,3,3 | cnt[2]=2,ans第2位赋值,cnt[2]-=1 | 0,2,2,4,4 |
基数排序是通过不停的收集和分配来对数据进行排序的。
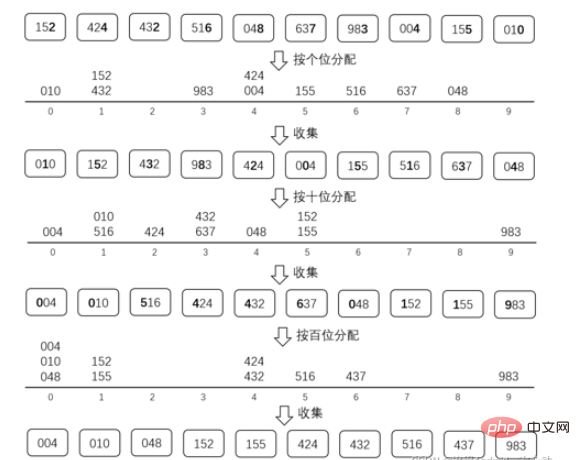
因为是10进制数,所以我们准备十个桶来存分配的数。
最大的数据是3位数,所以我们只需要进行3次收集和分配。
需要先从低位开始收集和分配(不可从高位开始排,如果从高位开始排的话,高位排好的顺序会在排低位的时候被打乱,有兴趣的话自己手写模拟一下试试就可以了)
在收集和分配的过程中,不要打乱已经排好的相对位置
比如按十位分配的时候,152和155这两个数的10位都是5,并且分配之前152在155的前面,那么收集的时候152还是要放在155之前的。
//基数排序
public static void radixSort(int[] array) {
//基数排序
//首先确定排序的趟数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;
//判断位数;
while (max > 0) {
max /= 10;
time++;
}
//建立10个队列;
List<ArrayList> queue = new ArrayList<ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList<Integer> queue1 = new ArrayList<Integer>();
queue.add(queue1);
}
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
//分配数组元素;
for (int j = 0; j < array.length; j++) {
//得到数字的第time+1位数;
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList<Integer> queue2 = queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}Atas ialah kandungan terperinci Bagaimana untuk melaksanakan sepuluh algoritma pengisihan teratas di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




