Cara membuat timbunan struktur data Java

Sifat timbunan

Timbunan secara logiknya adalah pokok binari yang lengkap dan timbunan itu disimpan secara fizikal dalam tatasusunan.

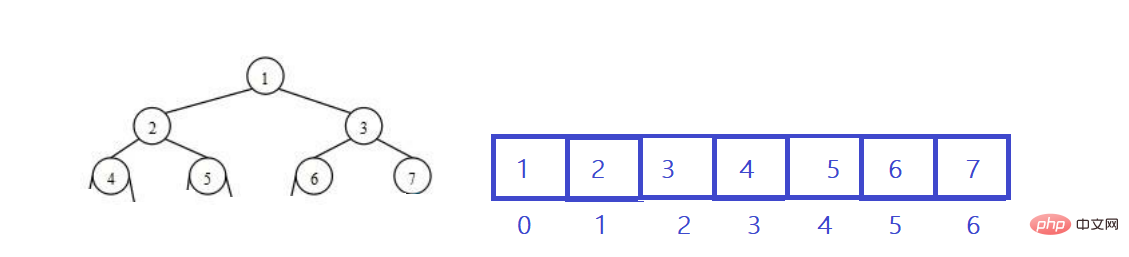
Ringkasan: Pepohon binari lengkap disimpan dalam tatasusunan menggunakan traversal tertib aras Penggunaan utama kaedah ini ialah perwakilan timbunan.

Dan jika subskrip ibu bapa diketahui,

maka: anak kiri (kiri) subskrip = 2 * ibu bapa + 1;

anak kanan (kanan ) subskrip = 2 * ibu bapa + 2;

anak yang dikenali (tiada perbezaan antara kiri dan kanan) (anak) subskrip, kemudian:

subskrip ibu bapa (ibu bapa) = (anak - 1) / 2;

Klasifikasi timbunan

Timbunan besar: Pokok binari lengkap di mana nod akar lebih besar daripada nod anak kiri dan kanan (nod induk lebih besar daripada nod anak), dipanggil a timbunan besar, atau timbunan akar yang besar, atau timbunan maksimum.

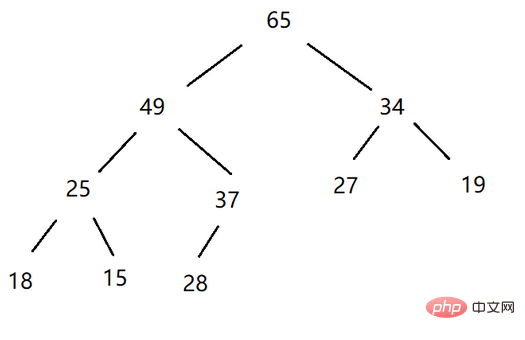
Timbunan kecil: Pokok binari lengkap di mana nod akar lebih kecil daripada nod anak kiri dan kanan dipanggil timbunan kecil (nod induk lebih kecil daripada anaknya nod), atau timbunan akar kecil, atau timbunan minimum.

Pelarasan ke bawah timbunan

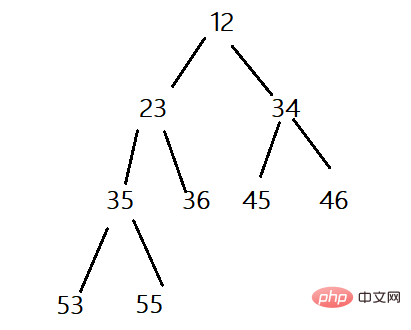
Kini terdapat tatasusunan, yang secara logiknya merupakan pokok binari yang lengkap Kita boleh menggunakan algoritma pelarasan ke bawah bermula dari nod akar kepada Ia menyesuaikan kepada longgokan kecil atau longgokan besar. Algoritma pelarasan ke bawah mempunyai premis: subpokok kiri dan kanan mestilah timbunan sebelum ia boleh dilaraskan.

Ambil timbunan kecil sebagai contoh:

1. Mula-mula, biarkan nod anak kiri dan kanan membandingkan dan ambil nilai minimum.

2. Bandingkan nod anak yang lebih kecil dengan nod induk Jika nod anak

3. Kitaran berulang Jika subskrip nod anak melintasi sempadan, ini bermakna ia telah sampai ke penghujungnya.

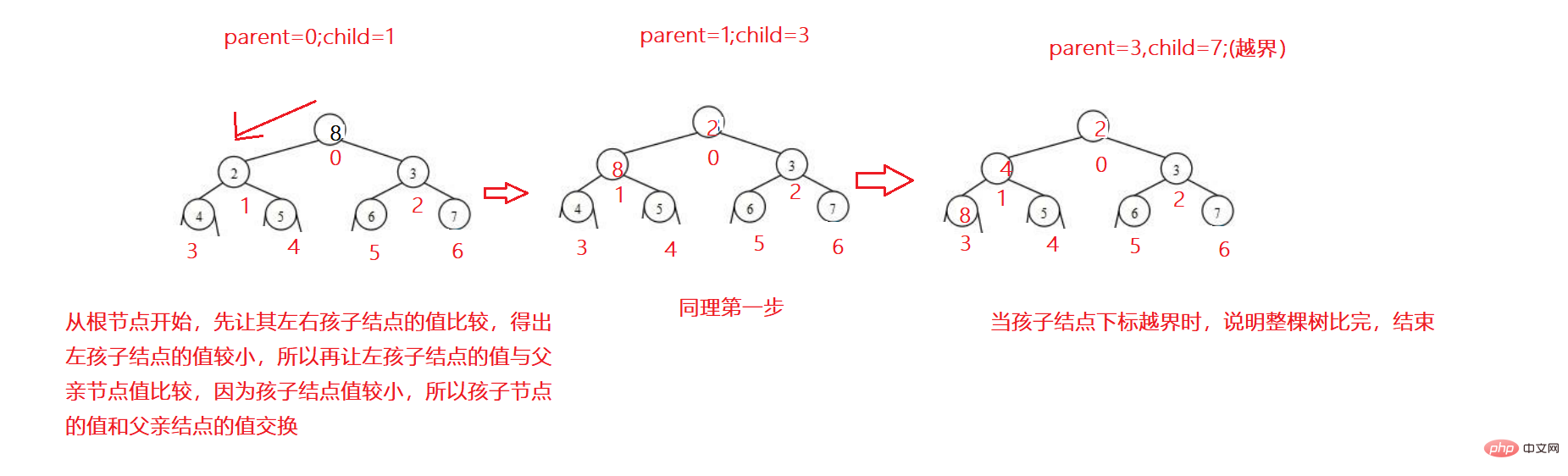
Contoh kod:

 //parent: 每棵树的根节点
 //len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
        int child=parent*2+1; //因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以最起码是有左孩子的，至少有1个孩子
        while(child<len){
            if(child+1<len && elem[child]<elem[child+1]){
                child++;//两孩子结点比较取较小值
            }
            if(elem[child]<elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
        }
    }

Penciptaan timbunan

Memandangkan tatasusunan, tatasusunan ini secara logiknya boleh dianggap sebagai pokok binari yang lengkap , tetapi ia belum menjadi timbunan (subpokok kiri dan kanan bukan besar atau kecil). Sekarang kita menggunakan algoritma untuk membinanya menjadi timbunan (besar atau kecil). Apa yang perlu dilakukan? Di sini kita mula melaraskan dari subpokok pertama nod bukan daun terakhir, dan melaraskannya sehingga ke pokok nod akar, dan kemudian kita boleh menyesuaikannya menjadi longgokan. Di sini kita akan menggunakan pelarasan ke bawah yang baru kita tulis.

public void creatHeap(int[] arr){
        for(int i=0;i<arr.length;i++){
            elem[i]=arr[i];
            useSize++;
        }
        for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
            shiftDown(parent,useSize);
        }
    }

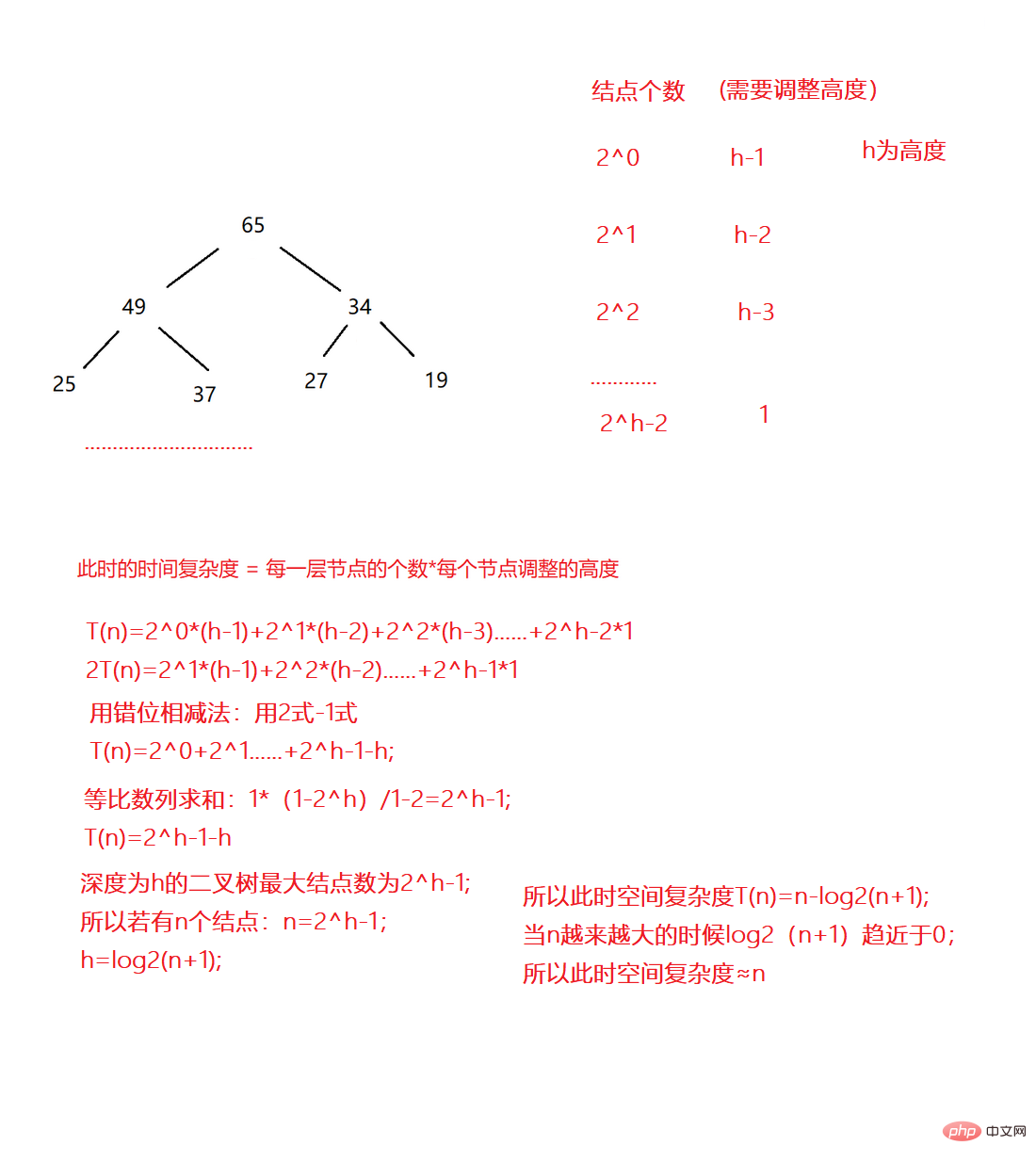
Kerumitan ruang membina timbunan ialah O(N), kerana timbunan itu adalah pokok binari yang lengkap, dan pokok binari penuh juga merupakan pokok binari yang lengkap Kami menggunakan pokok binari penuh (dalam kes terburuk) untuk membuktikannya.

Timbunan perlu dilaraskan ke atas

Sekarang terdapat timbunan, kita perlu memasukkan data di hujung timbunan dan kemudian melaraskannya supaya bahawa ia masih kekal dalam struktur timbunan, ini adalah pelarasan ke atas.

Ambil timbunan besar sebagai contoh:

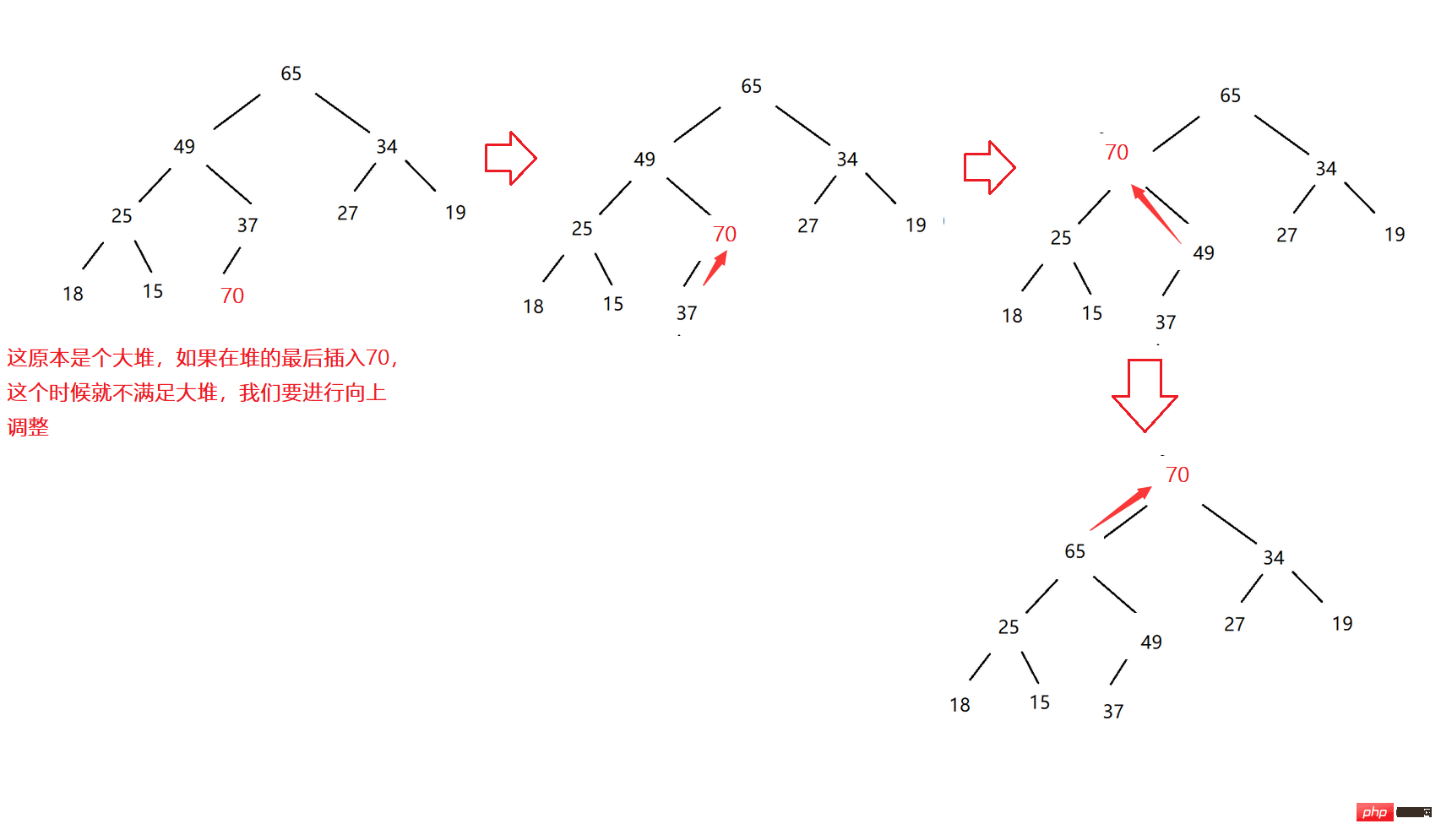
Contoh kod:

public void shiftup(int child){
        int parent=(child-1)/2;
        while(child>0){
            if(elem[child]>elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

Operasi biasa timbunan

Enqueue

Untuk menambah elemen pada timbunan, tambahkannya pada kedudukan terakhir, kemudian laraskannya ke atas.

public boolean isFull(){
        return elem.length==useSize;
    }
public void offer(int val){
        if(isFull()){
            elem= Arrays.copyOf(elem,2*elem.length);//扩容
        }
        elem[useSize++]=val;
        shiftup(useSize-1);
    }

Dequeue

Untuk memadamkan elemen dalam timbunan, tukar elemen atas timbunan dengan elemen terakhir, kemudian kurangkan saiz keseluruhan tatasusunan dengan satu, dan akhir sekali laraskannya ke bawah untuk memadam bahagian atas elemen timbunan.

public boolean isEmpty(){
        return useSize==0;
    }
public int poll(){
        if(isEmpty()){
            throw new RuntimeException("优先级队列为空");
        }
        int tmp=elem[0];
        elem[0]=elem[useSize-1];
        elem[useSize-1]=tmp;
        useSize--;
        shiftDown(0,useSize);
        return tmp;
    }

Dapatkan elemen pertama pasukan

public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("优先级队列为空");
        }
        return elem[0];
    }

Soalan Teratas

Beri anda 6 data, cari 3 data terbesar teratas. Bagaimanakah kita menggunakan timbunan pada masa ini?

Idea penyelesaian masalah:

1. Jika anda ingin mencari elemen K teratas yang terbesar, anda perlu membina timbunan akar yang kecil.

2. Jika anda ingin mencari elemen K terkecil yang pertama, anda perlu membina timbunan akar yang besar.

3. Elemen terbesar Kth. Bina timbunan kecil, dan unsur atas timbunan ialah unsur terbesar K.

4. Unsur terkecil Kth. Bina timbunan besar, dan elemen atas timbunan ialah unsur terbesar K.

Contoh

Contohnya: Cari data pertama n terbesar

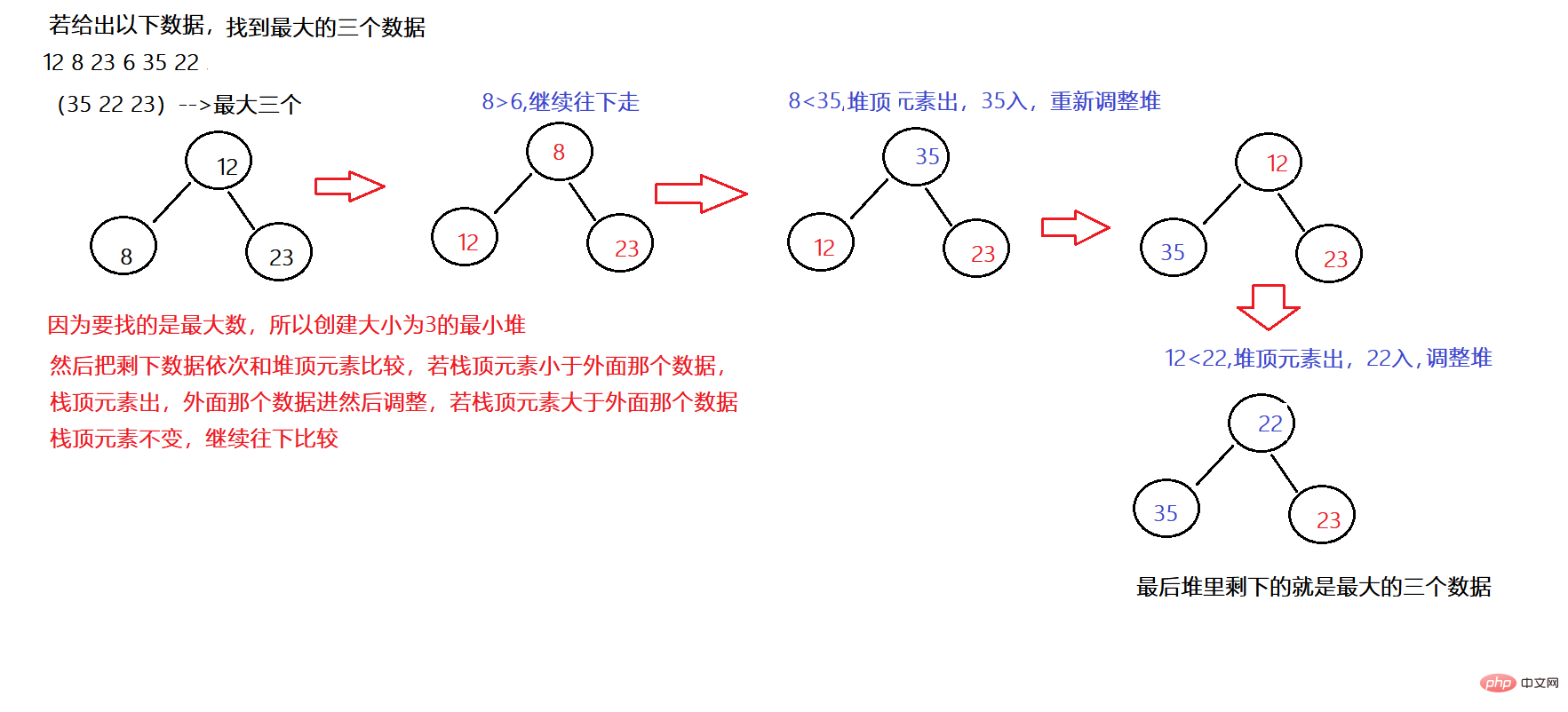
Contoh kod:

 public static int[] topK(int[] array,int k){
        //创建一个大小为K的小根堆
        PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });
        //遍历数组中元素，将前k个元素放入队列中
        for(int i=0;i<array.length;i++){
            if(minHeap.size()<k){
                minHeap.offer(array[i]);
            }else{
                //从k+1个元素开始，分别和堆顶元素比较
                int top=minHeap.peek();
                if(array[i]>top){
                    //先弹出后存入
                    minHeap.poll();
                    minHeap.offer(array[i]);
                }
            }
        }
        //将堆中元素放入数组中
        int[] tmp=new int[k];
        for(int i=0;i< tmp.length;i++){
            int top=minHeap.poll();
            tmp[i]=top;
        }
        return tmp;
    }
    public static void main(String[] args) {
        int[] array={12,8,23,6,35,22};
        int[] tmp=topK(array,3);
        System.out.println(Arrays.toString(tmp));
    }

Hasil: < .

---->Dagendui

Contoh kod:

  public void heapSort(){
        int end=useSize-1;
        while(end>0){
            int tmp=elem[0];
            elem[0]=elem[end];
            elem[end]=tmp;
            shiftDown(0,end);//假设这里向下调整为大根堆
            end--;
        }
    }

Atas ialah kandungan terperinci Cara membuat timbunan struktur data Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!