
Kerumitan pengiraan ialah ukuran sumber pengiraan (masa dan ruang) yang digunakan oleh algoritma tertentu semasa berjalan.
Kerumitan pengiraan terbahagi kepada dua kategori:
Kerumitan masa bukanlah ukuran algoritma atau sekeping kod yang dijalankan di bawah mesin atau mesin tertentu. keadaan. Kerumitan masa secara amnya merujuk kepada kerumitan masa, iaitu fungsi yang secara kualitatif menerangkan masa berjalan algoritma dan membolehkan kami membandingkan algoritma yang berbeza tanpa menjalankannya. Sebagai contoh, algoritma dengan O(n) akan sentiasa berprestasi lebih baik daripada O(n²) kerana kadar pertumbuhannya kurang daripada O(n²).
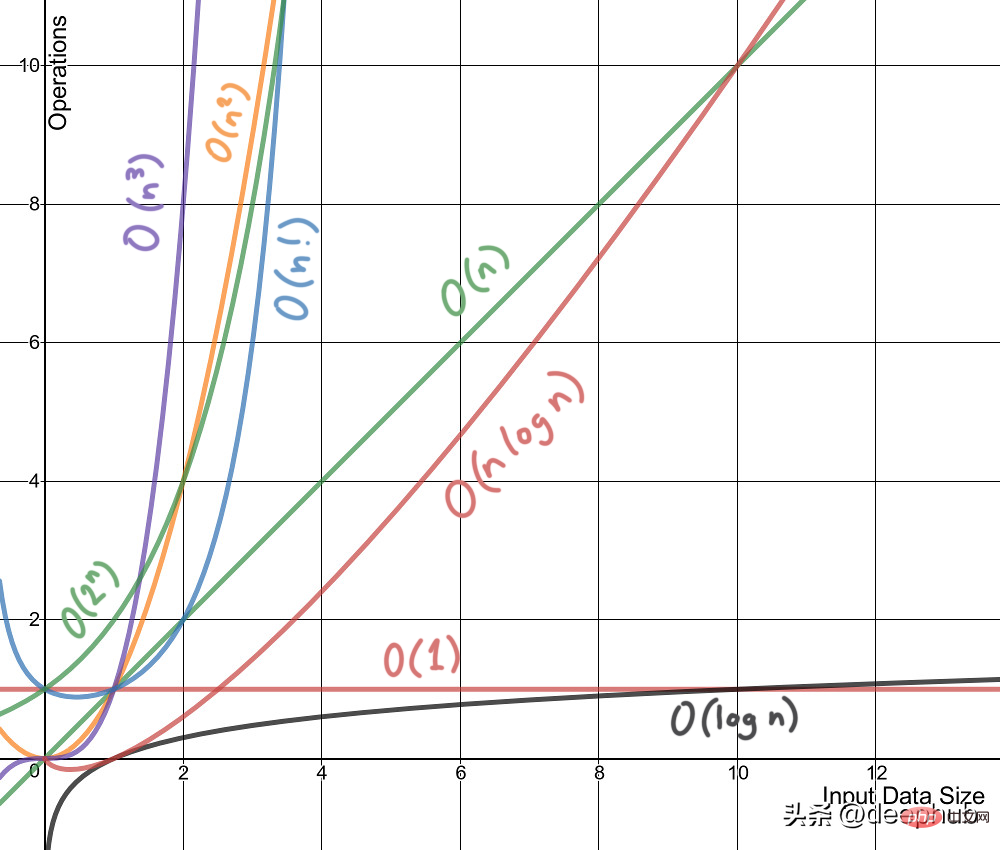
Sama seperti kerumitan masa ialah fungsi, begitu juga kerumitan ruang. Secara konsepnya ia sama dengan kerumitan masa, cuma gantikan masa dengan ruang. Wikipedia mentakrifkan kerumitan ruang sebagai:
Kerumitan ruang bagi algoritma atau program komputer ialah jumlah ruang storan yang diperlukan untuk menyelesaikan kejadian masalah pengiraan sebagai fungsi bilangan ciri sebagai input.
Di bawah ini kami telah menyusun kerumitan pengiraan beberapa algoritma pembelajaran mesin biasa.
n= bilangan sampel latihan, f = bilangan ciri, k= bilangan jiran terdekat
Brute:
kd-tree:
Atas ialah kandungan terperinci Ringkasan kerumitan pengiraan lapan algoritma pembelajaran mesin biasa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Algoritma penggantian halaman
Algoritma penggantian halaman
 Penggunaan kelas kalendar dalam java
Penggunaan kelas kalendar dalam java
 Bagaimana untuk menyambung semula penggunaan gas selepas pembayaran
Bagaimana untuk menyambung semula penggunaan gas selepas pembayaran
 Harga terkini riak
Harga terkini riak
 Bagaimana untuk memformat cakera keras dalam linux
Bagaimana untuk memformat cakera keras dalam linux
 Bagaimana untuk menyelesaikan masalah kegagalan pemasangan vs2008
Bagaimana untuk menyelesaikan masalah kegagalan pemasangan vs2008
 Kekunci pintasan penukaran tetingkap
Kekunci pintasan penukaran tetingkap
 Tukar teks kepada nilai angka
Tukar teks kepada nilai angka
 Perkhidmatan pecutan CDN tanpa pendaftaran
Perkhidmatan pecutan CDN tanpa pendaftaran




