 Peranti teknologi
Peranti teknologi
 AI
AI
 Bolehkah pembelajaran mesin benar-benar menghasilkan keputusan yang bijak?
Bolehkah pembelajaran mesin benar-benar menghasilkan keputusan yang bijak?
Bolehkah pembelajaran mesin benar-benar menghasilkan keputusan yang bijak?
Selepas tiga tahun, kami menamatkan pengajian pada 2022 Judy, pemenang Anugerah Turing, profesor sains komputer di University of California, Los Angeles, ahli akademik Akademi Sains Kebangsaan, dan dikenali sebagai "Bapa kepada Rangkaian Bayesian" Karya agung A. Perl "Penyebab: Model, Penaakulan dan Inferens".
Edisi pertama asal buku ini telah ditulis pada tahun 2000. Ia mempelopori idea dan kaedah analisis sebab akibat dan inferens yang mendapat pujian meluas sebaik sahaja ia diterbitkan dan mempromosikan sains data ., kecerdasan buatan, pembelajaran mesin, analisis sebab dan bidang lain telah memberi impak yang besar kepada komuniti akademik.
Kemudian, edisi kedua telah disemak pada tahun 2009. Kandungannya telah berubah dengan ketara berdasarkan perkembangan baharu dalam penyelidikan kausal pada masa itu. Versi bahasa Inggeris asal buku yang sedang kami terjemahkan telah diterbitkan pada tahun 2009, jadi sudah lebih sepuluh tahun yang lalu.
Penerbitan buku versi Cina ini akan membantu sarjana, pelajar dan pengamal Cina dalam pelbagai bidang memahami dan menguasai kandungan yang berkaitan dengan model sebab akibat, penaakulan dan inferens. Terutama dalam era semasa apabila statistik dan pembelajaran mesin popular, bagaimana untuk mencapai transformasi daripada "pemasangan data" kepada "pemahaman data"? Bagaimana untuk beralih daripada andaian dominan pada masa ini bahawa "semua pengetahuan datang daripada data itu sendiri" kepada paradigma pembelajaran mesin yang benar-benar baharu dalam dekad yang akan datang? Adakah ia akan mencetuskan "revolusi kecerdasan buatan kedua"?
Sama seperti Anugerah Turing dianugerahkan kepada Pearl, karyanya dinilai sebagai "sumbangan asas kepada bidang kecerdasan buatan. Dia mencadangkan algoritma penaakulan kemungkinan dan sebab, yang mengubah sepenuhnya peringkat awal kecerdasan buatan." Arah berdasarkan peraturan dan logik. "Kami menjangkakan paradigma ini membawa arah teknikal baharu dan momentum ke hadapan kepada pembelajaran mesin, dan akhirnya dapat memainkan peranan dalam aplikasi praktikal.
HanyaSeperti kata Pearl, "Pemasangan data pada masa ini dengan kukuh menguasai bidang semasa statistik dan pembelajaran mesin dan merupakan tumpuan utama kebanyakan penyelidik pembelajaran mesin hari ini. Paradigma penyelidikan, terutamanya mereka yang terlibat dalam sambungan, pembelajaran mendalam dan teknologi rangkaian saraf ini dengan "penyesuaian data" sebagai terasnya telah mencapai kejayaan besar dalam bidang aplikasi seperti penglihatan komputer, pengecaman pertuturan dan kejayaan yang menarik perhatian. Walau bagaimanapun, ramai penyelidik dalam bidang sains data juga menyedari bahawa, dalam amalan semasa, pembelajaran mesin tidak dapat menghasilkan jenis pemahaman yang diperlukan untuk membuat keputusan yang bijak. Isu ini termasuk: keteguhan, kebolehpindahan, kebolehtafsiran, dsb. Mari lihat contoh di bawah.
Adakah statistik boleh dipercayai?
Dalam beberapa tahun kebelakangan ini, ramai orang dalam media kendiri menganggap bahawa mereka adalah ahli statistik. Kerana "penyesuaian data" dan "semua pengetahuan datang daripada data itu sendiri" menyediakan asas statistik untuk banyak keputusan utama. Walau bagaimanapun, kita perlu berhati-hati semasa melakukan analisis ini. Lagipun, perkara mungkin tidak selalunya seperti yang kelihatan pada pandangan pertama! Kes yang berkait rapat dengan kehidupan kita. Sepuluh tahun yang lalu, harga rumah di pusat bandar ialah 8,000 yuan/meter persegi, dengan jumlah 10 juta meter persegi dijual di zon berteknologi tinggi, ia adalah 4,000 yuan/meter persegi, dengan jumlah 1 juta persegi; meter dijual secara keseluruhan, harga rumah purata di bandar ini ialah 7,636 yuan/meter persegi . Kini, harga di pusat bandar ialah 10,000 yuan/meter persegi, tetapi kerana bekalan tanah di pusat bandar kurang, hanya 2 juta meter persegi telah dijual zon berteknologi tinggi ialah 6,000 yuan/meter persegi, tetapi kerana terdapat lebih banyak tanah yang baru dibangunkan, 20 juta meter persegi telah dijual secara keseluruhan Lihatlah, harga purata rumah di bandar kini ialah 6,363 yuan/meter persegi; Oleh itu, melihat kawasan yang berbeza, harga perumahan telah meningkat secara individu, tetapi melihat secara keseluruhan, akan ada keraguan: Mengapa harga perumahan jatuh sekarang?
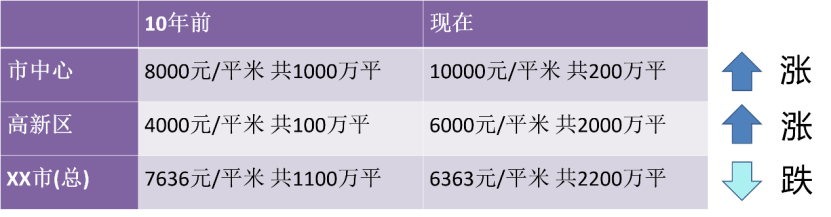
Rajah 1 Arah aliran harga perumahan dibahagikan dengan kawasan berbeza adalah bertentangan dengan kesimpulan keseluruhan
Kami tahu ini Fenomena itu dipanggil Simpson's Paradox. Kes-kes ini jelas menunjukkan bagaimana kita boleh mendapatkan model dan kesimpulan yang salah sepenuhnya daripada data statistik apabila kita tidak diberi pembolehubah yang diperhatikan yang mencukupi. Dalam kes wabak ini, kita biasanya mendapat statistik seluruh negara. Jika kita dikumpulkan mengikut wilayah atau bandar atau daerah, kita mungkin membuat kesimpulan yang sangat berbeza. Di seluruh negara, kita dapat melihat penurunan dalam bilangan kes COVID-19, walaupun sesetengah kawasan mengalami peningkatan kes (yang mungkin menandakan permulaan gelombang seterusnya). Ini juga mungkin berlaku jika terdapat kumpulan yang berbeza secara meluas, seperti kawasan dengan populasi yang berbeza secara meluas. Dalam data nasional, lonjakan dalam kes di kawasan kurang padat penduduk mungkin lebih kecil daripada penurunan di kawasan yang lebih padat penduduk.
Masalah statistik yang serupa berdasarkan "penyesuaian data" berlimpah. Ambil dua contoh menarik berikut.
Jika kami mengumpul data tentang bilangan filem yang dimainkan oleh Nicolas Cage dan bilangan lemas di Amerika Syarikat setiap tahun, kami akan mendapati bahawa kedua-dua pembolehubah ini sangat berkorelasi dan kesesuaian data adalah sangat tinggi.
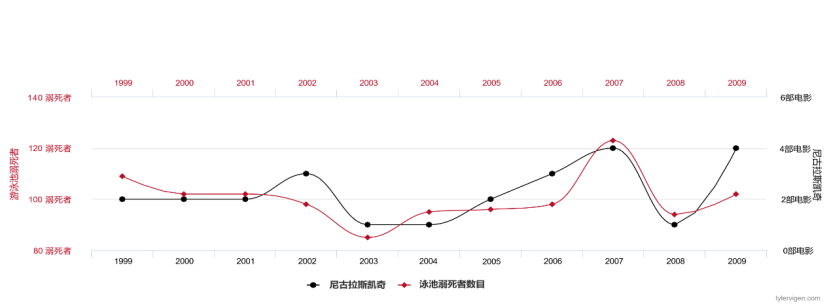
Rajah 2 Bilangan filem yang dimainkan oleh Nicolas Cage dan bilangan orang yang lemas di Amerika Syarikat setiap tahun
Jika kami mengumpul data jualan susu per kapita dan bilangan pemenang Hadiah Nobel di setiap negara, kami akan mendapati bahawa kedua-dua pembolehubah ini sangat berkorelasi.
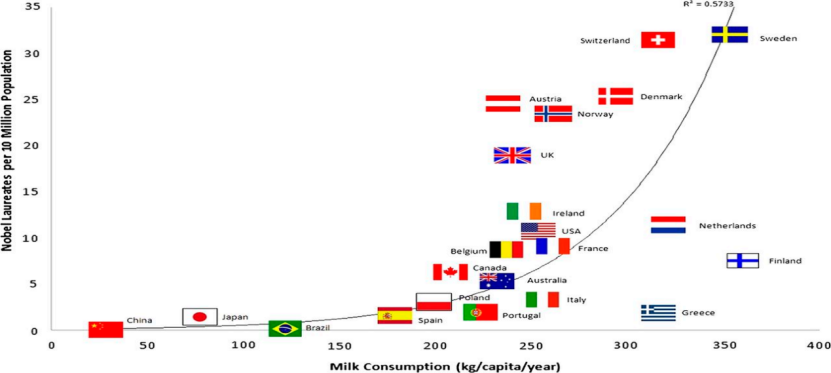
Rajah 3 Penggunaan susu per kapita dan bilangan Hadiah Nobel
Daripada akal kita Secara Intelek bercakap, ini adalah korelasi palsu, malah paradoks. Tetapi dari perspektif matematik dan teori kebarangkalian, kes-kes yang menunjukkan korelasi palsu atau paradoks tidak bermasalah kedua-duanya dari perspektif statistik dan pengiraan. Sesiapa sahaja yang mempunyai asas sebab-akibat tahu bahawa ini berlaku kerana terdapat apa yang dipanggil pembolehubah mengintai, pengacau yang tidak diperhatikan, tersembunyi dalam data.
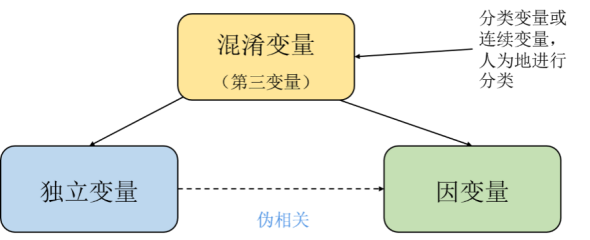
Rajah 4 Pembolehubah tidak bersandar membawa kepada korelasi palsu antara dua pembolehubah
Perl memberikan paradigma penyelesaian dalam "The Theory of Causation", menganalisis dan memperoleh masalah di atas secara terperinci, dan menekankan perbezaan penting antara sebab dan statistik, walaupun analisis sebab dan inferens masih berdasarkan statistik pembelajaran. Pearl mencadangkan model pengiraan asas operasi campur tangan (pengendali), termasuk prinsip pintu belakang dan formula pengiraan khusus Pada masa ini, ini merupakan perihalan sebab yang paling matematik. "Penyebab dan konsep yang berkaitan (seperti rawak, pengacau, campur tangan, dll.) bukanlah konsep statistik." Ini adalah prinsip asas yang dijalankan melalui pemikiran analisis sebab Pearl, yang disebut oleh Pearl sebagai prinsip pertama [2].
Jadi, kaedah pembelajaran mesin dipacu data semasa, terutamanya algoritma yang sangat bergantung pada kaedah statistik, berkemungkinan besar untuk mempelajari keputusan separuh benar dan separuh palsu . Ini kerana model-model ini cenderung untuk belajar berdasarkan pengedaran data yang diperhatikan, dan bukannya mekanisme yang mana data dijana.
2 Tiga isu yang perlu diselesaikan segera oleh pembelajaran mesin
Keteguhan: Dengan populariti kaedah pembelajaran mendalam, Computers Research dalam penglihatan, pemprosesan bahasa semula jadi dan pengecaman pertuturan menggunakan secara meluas struktur rangkaian neural dalam yang terkini. Tetapi masih terdapat fakta lama bahawa dalam dunia nyata, pengedaran data yang kami kumpulkan jarang lengkap dan mungkin tidak konsisten dengan pengedaran di dunia nyata. Dalam aplikasi penglihatan komputer, pengedaran set latihan dan data set ujian mungkin dipengaruhi oleh faktor seperti perbezaan piksel, kualiti mampatan atau anjakan kamera, putaran atau sudut. Pembolehubah ini sebenarnya adalah isu "intervensi" dalam konsep sebab dan akibat. Daripada ini, algoritma mudah telah dicadangkan untuk mensimulasikan campur tangan untuk menguji secara khusus kebolehan generalisasi model klasifikasi dan pengecaman, seperti pengimbangan ruang, kabur, perubahan dalam kecerahan atau kontras, kawalan latar belakang dan putaran, dan pemerolehan dalam pelbagai persekitaran dan lain-lain. Setakat ini, walaupun kami telah mencapai beberapa kemajuan dalam keteguhan menggunakan kaedah seperti penambahan data, pra-latihan dan pembelajaran penyeliaan kendiri, tidak ada konsensus yang jelas tentang cara menyelesaikan masalah ini. Telah dihujahkan bahawa pembetulan ini mungkin tidak mencukupi dan membuat generalisasi di luar andaian bebas dan teragih sama memerlukan pembelajaran bukan sahaja persatuan statistik antara pembolehubah tetapi juga model penyebab yang mendasari yang menjelaskan mekanisme yang mana data dijana dan membenarkan simulasi melalui campur tangan. konsep Perubahan taburan.
Kebolehpindahan: Pemahaman bayi tentang objek adalah berdasarkan penjejakan objek yang berkelakuan secara konsisten dari semasa ke semasa Pendekatan ini membolehkan bayi mempelajari tugas baharu dengan cepat kerana pengetahuan mereka tentang objek dan pemahaman intuitif boleh digunakan semula. Begitu juga, untuk dapat menyelesaikan tugas dunia sebenar dengan cekap memerlukan penggunaan semula pengetahuan dan kemahiran yang dipelajari dalam senario baharu. Penyelidikan telah membuktikan bahawa sistem pembelajaran mesin yang mempelajari pengetahuan alam sekitar adalah lebih cekap dan lebih serba boleh. Jika kita memodelkan dunia sebenar, banyak modul mempamerkan tingkah laku yang serupa dalam tugasan dan persekitaran yang berbeza. Oleh itu, apabila berhadapan dengan persekitaran atau tugas baharu, manusia atau mesin mungkin hanya perlu melaraskan beberapa modul dalam perwakilan dalaman mereka. Apabila mempelajari model kausal, memandangkan kebanyakan pengetahuan (iaitu, modul) boleh digunakan semula tanpa latihan lanjut, lebih sedikit sampel diperlukan untuk menyesuaikan diri dengan persekitaran atau tugasan baharu.
Kebolehtafsiran: Kebolehtafsiran ialah konsep halus yang tidak boleh diterangkan sepenuhnya menggunakan hanya bahasa logik Boolean atau kebarangkalian statistik, ia memerlukan konsep campur tangan tambahan, atau bahkan konsep kontrafaktual. Takrifan manipulasi dalam sebab bertumpu pada fakta bahawa kebarangkalian bersyarat ("Melihat orang membuka payung mereka menunjukkan bahawa hujan") tidak boleh meramalkan dengan pasti hasil campur tangan aktif ("Meletakkan payung anda tidak menghalangnya daripada hujan" ). Kausalitas dilihat sebagai sebahagian daripada rantaian inferens yang boleh memberikan ramalan untuk situasi yang jauh daripada taburan yang diperhatikan, malah boleh memberikan kesimpulan untuk senario hipotesis semata-mata. Dalam pengertian ini, menemui hubungan sebab akibat bermakna memperoleh pengetahuan yang boleh dipercayai yang tidak dihadkan oleh pengedaran data yang diperhatikan dan tugas latihan, sekali gus menyediakan spesifikasi yang tidak jelas untuk pembelajaran yang boleh ditafsir.
3. Tiga peringkat pemodelan pembelajaran kausal
Secara khusus, model pembelajaran mesin berdasarkan model statistik hanya boleh memodelkan hubungan korelasi, manakala Hubungan korelasi cenderung berubah dengan perubahan dalam pengedaran data; manakala model sebab adalah berdasarkan pemodelan hubungan sebab, yang menangkap intipati penjanaan data dan mencerminkan hubungan antara mekanisme penjanaan data lebih teguh dan mempunyai keupayaan untuk membuat generalisasi di luar pengedaran. Sebagai contoh, dalam teori keputusan, perbezaan antara sebab dan statistik adalah lebih jelas. Terdapat dua jenis masalah dalam teori keputusan Satu ialah persekitaran semasa diketahui, intervensi dirancang, dan hasilnya diramalkan. Jenis yang lain ialah mengetahui persekitaran dan keputusan semasa dan membuat kesimpulan punca. Yang pertama dipanggil masalah berbangkit, dan yang kedua dipanggil masalah penculikan [3].
Keupayaan ramalan di bawah keadaan bebas dan teragih serupa
Model statistik hanyalah penerangan cetek tentang dunia nyata yang diperhatikan kerana ia hanya menumpukan pada korelasi. Untuk sampel dan label, kami boleh menggunakan anggaran untuk menjawab soalan seperti: "Apakah kebarangkalian terdapat anjing dalam foto tertentu ini?" "Memandangkan beberapa simptom, apakah kebarangkalian kegagalan jantung?". Soalan sebegini boleh dijawab dengan memerhatikan data i.i.d yang cukup. Walaupun algoritma pembelajaran mesin boleh melakukan perkara ini dengan baik, ramalan yang tepat tidak mencukupi untuk membuat keputusan kami, dan pembelajaran kausal menyediakan tambahan yang berguna. Bagi contoh sebelumnya, kekerapan Nicolas Cage membintangi filem berkorelasi positif dengan kadar kematian lemas di Amerika Syarikat Kita sememangnya boleh melatih model pembelajaran statistik untuk meramalkan kadar kematian lemas di Amerika Syarikat berdasarkan kekerapan Nicolas Cage membintangi filem, tetapi jelas ini Tiada hubungan sebab akibat langsung antara kedua-duanya. Model statistik hanya tepat apabila ia diedarkan secara bebas dan sama Jika kita membuat sebarang intervensi untuk mengubah taburan data, ia akan menyebabkan ralat dalam model pembelajaran statistik.
Keupayaan meramal di bawah peralihan/intervensi pengedaran
Kami membincangkan lebih lanjut masalah intervensi, yang lebih mencabar kerana intervensi (operasi) akan membawa kita keluar daripada pengagihan bebas dan sama dalam pembelajaran statistik . Meneruskan contoh Nicolas Cage, "Adakah menambah bilangan filem Nicolas Cage tahun ini meningkatkan kadar lemas di Amerika Syarikat?" Jelas sekali, campur tangan manusia akan menyebabkan pengedaran data berubah, dan syarat untuk pembelajaran statistik untuk terus hidup akan dipecahkan, jadi ia akan gagal. Sebaliknya, jika kita boleh mempelajari model ramalan dengan adanya campur tangan, maka ini berpotensi membolehkan kita mendapatkan model yang lebih teguh kepada perubahan pengagihan dalam tetapan dunia sebenar. Sebenarnya, apa yang dipanggil campur tangan di sini bukanlah sesuatu yang baru, banyak perkara yang berubah mengikut masa, seperti pilihan minat orang ramai, atau terdapat ketidakpadanan dalam pengedaran set latihan dan set ujian itu sendiri. Seperti yang telah kami nyatakan sebelum ini, keteguhan rangkaian saraf telah mendapat lebih banyak perhatian dan telah menjadi topik penyelidikan yang berkait rapat dengan inferens sebab akibat. Ramalan dalam kes peralihan pengedaran tidak boleh dihadkan untuk mencapai ketepatan yang tinggi pada set ujian Jika kita berharap untuk menggunakan algoritma pembelajaran mesin dalam aplikasi praktikal, maka kita mesti percaya bahawa keputusan ramalan model juga akan berubah apabila keadaan persekitaran berubah. tepat. Kategori anjakan pengedaran dalam aplikasi praktikal mungkin pelbagai Model hanya mencapai keputusan yang baik pada beberapa set ujian tidak bermakna kita boleh mempercayai model ini dalam apa jua keadaan Set ujian ini hanya sesuai dengan set ujian ini . Agar kita boleh mempercayai model ramalan dalam seberapa banyak situasi yang mungkin, kita mesti menggunakan model yang mempunyai keupayaan untuk menjawab soalan intervensi, sekurang-kurangnya bukan hanya menggunakan model pembelajaran statistik.
Keupayaan untuk menjawab soalan berlawanan
Soalan berlawanan melibatkan penaakulan tentang mengapa perkara itu berlaku, membayangkan akibat daripada melakukan tindakan yang berbeza, dan daripada ini, anda boleh membuat keputusan untuk mengambil tindakan untuk mencapai hasil yang diinginkan. Menjawab soalan berlawanan adalah lebih sukar daripada campur tangan, tetapi ia juga merupakan cabaran kritikal untuk AI. Jika soalan intervensi ialah "Apakah yang akan berlaku kepada risiko kegagalan jantung pesakit jika kita mula bersenam secara teratur sekarang?", soalan balas yang sepadan ialah "Bagaimana jika pesakit yang telah mengalami kegagalan jantung ini mula bersenam setahun yang lalu?" , adakah dia masih akan mengalami kegagalan jantung?" Jelas sekali menjawab soalan berlawanan fakta adalah sangat penting untuk pembelajaran pengukuhan. Mereka boleh merenung keputusan mereka sendiri, merumuskan hipotesis berlawanan, dan kemudian mengesahkannya melalui amalan, sama seperti sains kita. Penyelidikan adalah sama.
4. Aplikasi pembelajaran kausal
Akhir sekali, mari kita lihat cara mengaplikasikan pembelajaran kausal dalam pelbagai bidang. Hadiah Nobel dalam Sains Ekonomi 2021 telah dianugerahkan kepada Joshua D. Angrist dan Guido W. Imbens untuk "sumbangan metodologi mereka kepada analisis hubungan sebab akibat." Mereka mengkaji aplikasi inferens sebab dalam ekonomi buruh empirikal. Jawatankuasa pemilihan Hadiah Nobel dalam Ekonomi percaya bahawa "eksperimen semula jadi (eksperimen rawak atau terkawal) boleh membantu menjawab soalan penting", tetapi cara "menggunakan data pemerhatian untuk menjawab hubungan sebab akibat" adalah lebih mencabar. Persoalan penting dalam ekonomi ialah persoalan sebab musabab. Sebagai contoh, bagaimanakah pendatang mempengaruhi prospek pasaran buruh penduduk tempatan? Bolehkah belajar untuk sekolah siswazah meningkatkan pendapatan? Apakah kesan gaji minimum terhadap prospek pekerjaan pekerja mahir? Soalan-soalan ini sukar untuk dijawab kerana kita tidak mempunyai cara yang betul untuk mentafsir kontrafaktual.
Sejak 1970-an, ahli statistik telah mencipta rangka kerja untuk mengira "counterfactuals" untuk mendedahkan kesan sebab akibat antara dua pembolehubah. Atas dasar ini, ahli ekonomi telah membangunkan lagi kaedah seperti regresi ketakselanjaran, perbezaan dalam perbezaan, dan skor kecenderungan, dan telah menggunakan kaedah tersebut secara meluas dalam penyelidikan kausal mengenai pelbagai isu dasar ekonomi. Daripada teks agama dari abad ke-6 hingga pembelajaran mesin penyebab pada tahun 2021, termasuk pemprosesan bahasa semula jadi penyebab, kita boleh menggunakan pembelajaran mesin, statistik dan ekonometrik untuk memodelkan kesan sebab akibat. Analisis dalam ekonomi dan sains sosial lain terutamanya berkisar pada anggaran kesan sebab akibat, iaitu kesan campur tangan pembolehubah ciri ke atas pembolehubah hasil. Sebenarnya, dalam kebanyakan kes, perkara yang kami minati ialah apa yang dipanggil kesan campur tangan. Kesan intervensi merujuk kepada kesan sebab akibat intervensi atau rawatan ke atas pembolehubah hasil. Sebagai contoh, dalam ekonomi, salah satu kesan campur tangan yang paling banyak dianalisis ialah kesan penyebab subsidi kepada syarikat terhadap pendapatan korporat. Untuk tujuan ini, Rubin mencadangkan rangka kerja hasil yang berpotensi.
Walaupun ahli ekonomi dan saintis sosial lain lebih berkebolehan menganggarkan kesan sebab akibat yang tepat berbanding ramalan, mereka juga berminat dengan kelebihan ramalan kaedah pembelajaran mesin. Contohnya, keupayaan ramalan sampel yang tepat atau keupayaan untuk mengendalikan sejumlah besar ciri. Tetapi seperti yang telah kita lihat, model pembelajaran mesin klasik tidak direka bentuk untuk menganggarkan kesan penyebab, dan menggunakan kaedah ramalan di luar rak daripada pembelajaran mesin boleh membawa kepada anggaran berat sebelah kesan sebab akibat. Kemudian, kita mesti menambah baik teknik pembelajaran mesin sedia ada untuk memanfaatkan pembelajaran mesin untuk menganggar kesan sebab akibat secara berterusan dan berkesan, yang membawa kepada kelahiran pembelajaran mesin penyebab!
Pada masa ini, pembelajaran mesin penyebab boleh dibahagikan secara kasar kepada dua arah penyelidikan mengikut jenis kesan penyebab yang akan dianggarkan. Satu hala tuju yang penting ialah memperbaik kaedah pembelajaran mesin untuk anggaran yang tidak berat sebelah dan konsisten bagi kesan intervensi purata. Model dalam bidang penyelidikan ini cuba menjawab soalan berikut: Apakah purata tindak balas pelanggan terhadap kempen pemasaran? Apakah kesan purata perubahan harga ke atas jualan? Tambahan pula, satu lagi barisan pembangunan dalam penyelidikan pembelajaran mesin kausal ditumpukan pada penambahbaikan kaedah pembelajaran mesin untuk mendedahkan kekhususan kesan intervensi, iaitu, mengenal pasti subpopulasi individu yang mempunyai kesan intervensi yang lebih besar atau lebih kecil daripada purata. Jenis model ini bertujuan untuk menjawab soalan berikut: Pelanggan manakah yang paling bertindak balas terhadap kempen pemasaran? Bagaimanakah kesan perubahan harga pada jualan berbeza mengikut umur pelanggan?
Selain contoh langsung ini, kami juga dapat merasakan bahawa sebab yang lebih mendalam mengapa pembelajaran mesin penyebab telah menarik minat saintis data ialah keupayaan generalisasi model. Model pembelajaran mesin yang menerangkan hubungan sebab akibat antara data boleh digeneralisasikan kepada persekitaran baharu, tetapi ini kekal sebagai salah satu cabaran terbesar dalam pembelajaran mesin hari ini.
Perl menganalisis isu ini pada tahap yang lebih mendalam dan percaya bahawa jika mesin tidak dapat menaakul secara bersebab, kita tidak akan pernah mencapai kecerdasan buatan peringkat manusia yang sebenar, kerana kausaliti adalah sesuatu yang kita manusia proses dan Memahami mekanisme utama dunia yang kompleks di sekeliling anda. Pearl menulis dalam kata pengantar kepada "On Causality" versi Cina bahawa "dalam dekad yang akan datang, rangka kerja ini akan digabungkan dengan sistem pembelajaran mesin sedia ada, yang berpotensi mencetuskan 'revolusi penyebab kedua.' Saya berharap buku ini juga boleh membolehkan bahasa Cina pembaca untuk mengambil bahagian secara aktif dalam revolusi yang akan datang ini.”
Atas ialah kandungan terperinci Bolehkah pembelajaran mesin benar-benar menghasilkan keputusan yang bijak?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Laman web ini melaporkan pada 27 Jun bahawa Jianying ialah perisian penyuntingan video yang dibangunkan oleh FaceMeng Technology, anak syarikat ByteDance Ia bergantung pada platform Douyin dan pada asasnya menghasilkan kandungan video pendek untuk pengguna platform tersebut Windows , MacOS dan sistem pengendalian lain. Jianying secara rasmi mengumumkan peningkatan sistem keahliannya dan melancarkan SVIP baharu, yang merangkumi pelbagai teknologi hitam AI, seperti terjemahan pintar, penonjolan pintar, pembungkusan pintar, sintesis manusia digital, dsb. Dari segi harga, yuran bulanan untuk keratan SVIP ialah 79 yuan, yuran tahunan ialah 599 yuan (nota di laman web ini: bersamaan dengan 49.9 yuan sebulan), langganan bulanan berterusan ialah 59 yuan sebulan, dan langganan tahunan berterusan ialah 499 yuan setahun (bersamaan dengan 41.6 yuan sebulan) . Di samping itu, pegawai yang dipotong juga menyatakan bahawa untuk meningkatkan pengalaman pengguna, mereka yang telah melanggan VIP asal
 Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
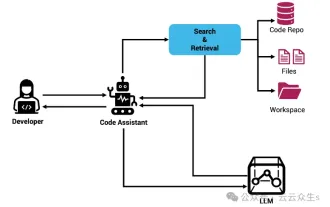
Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
Tingkatkan produktiviti, kecekapan dan ketepatan pembangun dengan menggabungkan penjanaan dipertingkatkan semula dan memori semantik ke dalam pembantu pengekodan AI. Diterjemah daripada EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, pengarang JanakiramMSV. Walaupun pembantu pengaturcaraan AI asas secara semulajadi membantu, mereka sering gagal memberikan cadangan kod yang paling relevan dan betul kerana mereka bergantung pada pemahaman umum bahasa perisian dan corak penulisan perisian yang paling biasa. Kod yang dijana oleh pembantu pengekodan ini sesuai untuk menyelesaikan masalah yang mereka bertanggungjawab untuk menyelesaikannya, tetapi selalunya tidak mematuhi piawaian pengekodan, konvensyen dan gaya pasukan individu. Ini selalunya menghasilkan cadangan yang perlu diubah suai atau diperhalusi agar kod itu diterima ke dalam aplikasi
 Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Untuk mengetahui lebih lanjut tentang AIGC, sila layari: 51CTOAI.x Komuniti https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou berbeza daripada bank soalan tradisional yang boleh dilihat di mana-mana sahaja di Internet memerlukan pemikiran di luar kotak. Model Bahasa Besar (LLM) semakin penting dalam bidang sains data, kecerdasan buatan generatif (GenAI) dan kecerdasan buatan. Algoritma kompleks ini meningkatkan kemahiran manusia dan memacu kecekapan dan inovasi dalam banyak industri, menjadi kunci kepada syarikat untuk kekal berdaya saing. LLM mempunyai pelbagai aplikasi Ia boleh digunakan dalam bidang seperti pemprosesan bahasa semula jadi, penjanaan teks, pengecaman pertuturan dan sistem pengesyoran. Dengan belajar daripada sejumlah besar data, LLM dapat menjana teks
 Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Model Bahasa Besar (LLM) dilatih pada pangkalan data teks yang besar, di mana mereka memperoleh sejumlah besar pengetahuan dunia sebenar. Pengetahuan ini dibenamkan ke dalam parameter mereka dan kemudiannya boleh digunakan apabila diperlukan. Pengetahuan tentang model ini "diperbaharui" pada akhir latihan. Pada akhir pra-latihan, model sebenarnya berhenti belajar. Selaraskan atau perhalusi model untuk mempelajari cara memanfaatkan pengetahuan ini dan bertindak balas dengan lebih semula jadi kepada soalan pengguna. Tetapi kadangkala pengetahuan model tidak mencukupi, dan walaupun model boleh mengakses kandungan luaran melalui RAG, ia dianggap berfaedah untuk menyesuaikan model kepada domain baharu melalui penalaan halus. Penalaan halus ini dilakukan menggunakan input daripada anotasi manusia atau ciptaan LLM lain, di mana model menemui pengetahuan dunia sebenar tambahan dan menyepadukannya
 Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) set data memainkan peranan penting dalam mempromosikan penyelidikan pemprosesan bahasa semula jadi (NLP). Set data QA berkualiti tinggi bukan sahaja boleh digunakan untuk memperhalusi model, tetapi juga menilai dengan berkesan keupayaan model bahasa besar (LLM), terutamanya keupayaan untuk memahami dan menaakul tentang pengetahuan saintifik. Walaupun pada masa ini terdapat banyak set data QA saintifik yang meliputi bidang perubatan, kimia, biologi dan bidang lain, set data ini masih mempunyai beberapa kekurangan. Pertama, borang data adalah agak mudah, kebanyakannya adalah soalan aneka pilihan. Ia mudah dinilai, tetapi mengehadkan julat pemilihan jawapan model dan tidak dapat menguji sepenuhnya keupayaan model untuk menjawab soalan saintifik. Sebaliknya, Soal Jawab terbuka
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada
 Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Editor |. KX Dalam bidang penyelidikan dan pembangunan ubat, meramalkan pertalian pengikatan protein dan ligan dengan tepat dan berkesan adalah penting untuk pemeriksaan dan pengoptimuman ubat. Walau bagaimanapun, kajian semasa tidak mengambil kira peranan penting maklumat permukaan molekul dalam interaksi protein-ligan. Berdasarkan ini, penyelidik dari Universiti Xiamen mencadangkan rangka kerja pengekstrakan ciri berbilang mod (MFE) novel, yang buat pertama kalinya menggabungkan maklumat mengenai permukaan protein, struktur dan jujukan 3D, dan menggunakan mekanisme perhatian silang untuk membandingkan ciri modaliti yang berbeza penjajaran. Keputusan eksperimen menunjukkan bahawa kaedah ini mencapai prestasi terkini dalam meramalkan pertalian mengikat protein-ligan. Tambahan pula, kajian ablasi menunjukkan keberkesanan dan keperluan maklumat permukaan protein dan penjajaran ciri multimodal dalam rangka kerja ini. Penyelidikan berkaitan bermula dengan "S
 Meletakkan pasaran seperti AI, GlobalFoundries memperoleh teknologi gallium nitrida Tagore Technology dan pasukan berkaitan
Jul 15, 2024 pm 12:21 PM
Meletakkan pasaran seperti AI, GlobalFoundries memperoleh teknologi gallium nitrida Tagore Technology dan pasukan berkaitan
Jul 15, 2024 pm 12:21 PM
Menurut berita dari laman web ini pada 5 Julai, GlobalFoundries mengeluarkan kenyataan akhbar pada 1 Julai tahun ini, mengumumkan pemerolehan teknologi power gallium nitride (GaN) Tagore Technology dan portfolio harta intelek, dengan harapan dapat mengembangkan bahagian pasarannya dalam kereta dan Internet of Things dan kawasan aplikasi pusat data kecerdasan buatan untuk meneroka kecekapan yang lebih tinggi dan prestasi yang lebih baik. Memandangkan teknologi seperti AI generatif terus berkembang dalam dunia digital, galium nitrida (GaN) telah menjadi penyelesaian utama untuk pengurusan kuasa yang mampan dan cekap, terutamanya dalam pusat data. Laman web ini memetik pengumuman rasmi bahawa semasa pengambilalihan ini, pasukan kejuruteraan Tagore Technology akan menyertai GLOBALFOUNDRIES untuk membangunkan lagi teknologi gallium nitride. G



