1. Penilaian ungkapan aritmetik
Untuk menghuraikan jenis teks ini, satu lagi peraturan tatabahasa yang khusus diperlukan. Kami memperkenalkan di sini peraturan tatabahasa Backus Normal Form (BNF) dan Extended Backus Normal Form (EBNF) yang boleh mewakili tatabahasa bebas konteks. Daripada sekecil ungkapan operasi aritmetik kepada sebesar hampir semua bahasa pengaturcaraan, ia ditakrifkan menggunakan tatabahasa tanpa konteks.
Untuk ungkapan operasi aritmetik yang mudah, diandaikan bahawa kami telah menggunakan teknologi pembahagian perkataan untuk menukarnya kepada aliran token input, seperti NUM+NUM*NUM (lihat catatan blog sebelumnya untuk kaedah pembahagian perkataan).
Atas dasar ini, kami mentakrifkan peraturan BNF seperti berikut:
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUMSalin selepas log masuk
Sudah tentu kaedah ini tidak cukup ringkas dan jelas Apa yang sebenarnya kami gunakan ialah borang EBNF:
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMSalin selepas log masuk
Setiap peraturan BNF dan EBNF (ungkapan dalam bentuk ::=) boleh dianggap sebagai penggantian, iaitu simbol di sebelah kiri boleh digantikan dengan simbol di sebelah kanan. Kami cuba menggunakan BNF/EBNF untuk memadankan teks input dengan peraturan tatabahasa semasa proses penghuraian untuk melengkapkan pelbagai penggantian dan pengembangan. Dalam EBNF, peraturan yang diletakkan dalam {...}* adalah pilihan dan * menunjukkan bahawa peraturan itu boleh diulang sifar atau lebih kali (bersamaan dengan ungkapan biasa).
Rajah berikut dengan jelas menunjukkan hubungan antara bahagian "rekursi" dan "keturunan" bagi penghurai turunan rekursif (penghurai) dan ENBF:
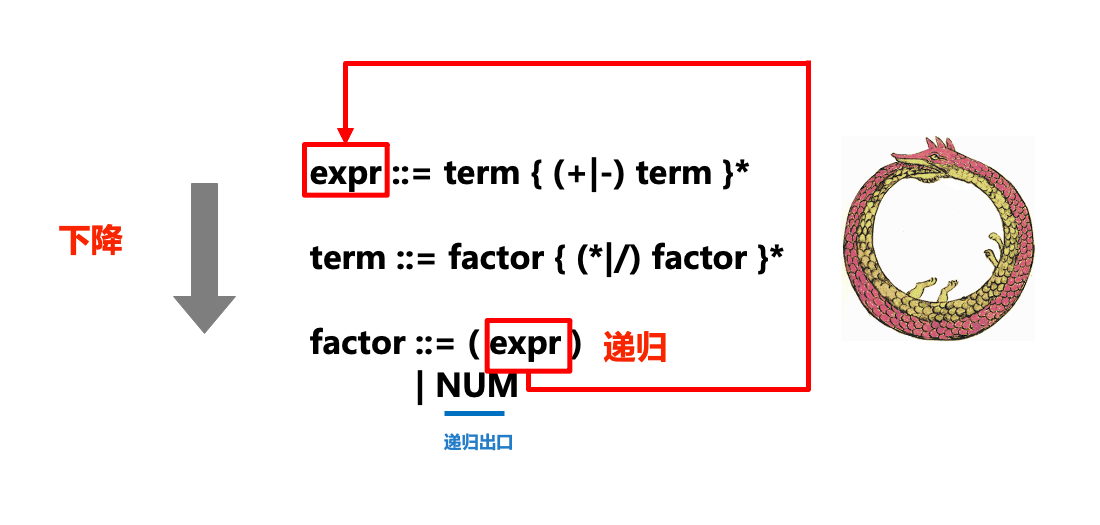
Dalam amalan Semasa proses penghuraian, kami mengimbas aliran token dari kiri ke kanan, dan memproses token semasa proses pengimbasan Jika ia tersekat, ralat sintaks akan dihasilkan. Setiap peraturan tatabahasa ditukar kepada fungsi atau kaedah Contohnya, peraturan ENBF di atas ditukar kepada kaedah berikut:
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...Salin selepas log masuk
Dalam proses memanggil kaedah yang sepadan dengan peraturan, jika kita menemui simbol seterusnya. Jika kita perlu menggunakan peraturan lain untuk dipadankan, kita akan "menurun" ke kaedah peraturan lain (seperti memanggil istilah dalam expr dan faktor dalam istilah), iaitu bahagian "menurun" daripada keturunan rekursif.
Kadangkala kaedah yang sudah dilaksanakan dipanggil (contohnya, istilah dipanggil dalam expr, faktor dipanggil dalam istilah, dan expr dipanggil dalam faktor, yang bersamaan dengan ouroboros), iaitu keturunan rekursif. Bahagian "rekursif".
Untuk bahagian berulang yang muncul dalam tatabahasa (seperti expr ::= term { (+|-) term }*), kami melaksanakannya melalui gelung sementara.
Mari kita lihat pelaksanaan kod khusus. Yang pertama ialah bahagian segmentasi perkataan Mari kita rujuk artikel sebelum ini untuk memperkenalkan kod blog segmentasi perkataan.
import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格，\s表示空格，+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tokSalin selepas log masuk
Berikut ialah pelaksanaan khusus penilai ungkapan:
class ExpressionEvaluator():
""" 递归下降的Parser实现，每个语法规则都对应一个方法，
使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token，下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配，则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配，如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则，每个语法规则对应一个方法
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")Salin selepas log masuk
Kami memasukkan ungkapan berikut untuk ujian:
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))Salin selepas log masuk
Hasil penilaian adalah seperti berikut:
2
5
14
37
Jika teks yang kami masukkan tidak mematuhi peraturan tatabahasa:
print(e.parse("2 + (3 + * 4)"))Salin selepas log masuk
, a Pengecualian SyntaxError akan dilemparkan: Expected NUMBER or LPAREN.
Ringkasnya, dapat dilihat bahawa algoritma penilaian ekspresi kami berjalan dengan betul.
2. Hasilkan pokok ekspresi
Di atas kita mendapat hasil ungkapan, tetapi bagaimana jika kita ingin menganalisis struktur ungkapan dan menjana pokok penghuraian ungkapan yang mudah? Kemudian kita perlu membuat pengubahsuaian tertentu kepada kaedah kelas di atas:
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")Salin selepas log masuk
Masukkan ungkapan berikut untuk menguji:
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))Salin selepas log masuk
Berikut ialah hasil yang dijana:
('+ ', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+' , 3, 4) , 5))
('+', ('+', 2, 3), 4)
Anda dapat melihat bahawa pokok ungkapan dijana dengan betul.
Contoh kami di atas adalah sangat mudah, tetapi penghurai keturunan rekursif juga boleh digunakan untuk melaksanakan penghurai yang agak kompleks Contohnya, kod Python dihuraikan melalui penghurai keturunan rekursif. Jika anda berminat dengan ini, anda boleh menyemak fail Grammar dalam kod sumber Python untuk mengetahui. Walau bagaimanapun, seperti yang akan kita lihat di bawah, menulis parser sendiri datang dengan pelbagai perangkap dan cabaran.
Rekursi kiri dan perangkap keutamaan pengendali
Sebarang peraturan tatabahasa yang melibatkan bentuk rekursi kiri tidak boleh diselesaikan oleh penghurai keturunan rekursif. Apa yang dipanggil rekursi kiri bermaksud bahawa simbol paling kiri di sebelah kanan ungkapan peraturan ialah pengepala peraturan Contohnya, untuk peraturan berikut:
items ::= items ',' item
| itemSalin selepas log masuk
Untuk melengkapkan analisis, anda boleh mentakrifkan kaedah berikut. :
def items(self):
itemsval = self.items() # 取第一项，然而此处会无穷递归！
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]Salin selepas log masuk
Ini akan Dalam baris pertama, self.items() dipanggil tak terhingga, mengakibatkan ralat pengulangan tak terhingga.
Terdapat juga ralat dalam peraturan tatabahasa itu sendiri, seperti keutamaan pengendali. Jika kita mengabaikan keutamaan pengendali, kita boleh secara langsung memudahkan ungkapan seperti berikut:
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUMSalin selepas log masuk
PYTHON Salin skrin penuh
Sintaks ini boleh dilaksanakan secara teknikal, tetapi konvensyen susunan pengiraan tidak diikuti, mengakibatkan "3+4 *5" menilai kepada 35 dan bukannya 23 yang dijangkakan. Oleh itu, peraturan expr dan istilah yang berasingan diperlukan untuk memastikan ketepatan keputusan pengiraan.
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan Parser keturunan rekursif dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
