Analisis kod contoh algoritma carian dan pengisihan Python

Cari

Carian binari

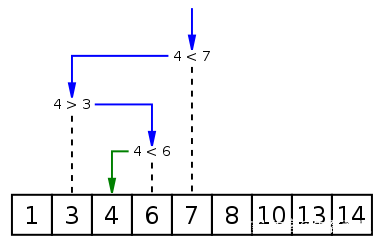
Carian binari ialah satu cara untuk mencari nilai tertentu dalam tatasusunan tertib Algoritma carian elemen. Proses carian bermula dari elemen tengah tatasusunan, dan jika elemen tengah menjadi elemen yang ditemui, proses carian akan tamat jika elemen tertentu lebih besar atau kurang daripada elemen tengah, carian dilakukan dalam separuh daripada tatasusunan yang lebih besar daripada atau kurang daripada elemen tengah, dan Sama seperti permulaan, mulakan perbandingan dari elemen tengah. Jika tatasusunan kosong pada langkah tertentu, ini bermakna ia tidak dapat ditemui. Algoritma carian ini mengurangkan julat carian sebanyak separuh dengan setiap perbandingan.

# 返回 x 在 arr 中的索引，如果不存在返回 -1
def binarySearch (arr, l, r, x):
    # 基本判断
    if r >= l:
        mid = int(l + (r - l)/2)
        # 元素整好的中间位置
        if arr[mid] == x:
            return mid
        # 元素小于中间位置的元素，只需要再比较左边的元素
        elif arr[mid] > x:
            return binarySearch(arr, l, mid-1, x)
        # 元素大于中间位置的元素，只需要再比较右边的元素
        else:
            return binarySearch(arr, mid+1, r, x)
    else:
        # 不存在
        return -1
 
# 测试数组
arr = [ 2, 3, 4, 10, 40]
x = int(input('请输入元素：'))
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
 
if result != -1:
    print("元素在数组中的索引为 %d" % result)
else:
    print("元素不在数组中")

Hasil jalankan:

Sila masukkan elemen: 4
Indeks elemen dalam tatasusunan ialah 2

Sila masukkan elemen: 5
Elemen tiada dalam tatasusunan

Carian linear

Carian linear: Ia merujuk kepada menyemak setiap elemen dalam tatasusunan dalam susunan tertentu sehingga nilai khusus yang anda cari ditemui.

def search(arr, n, x):
    for i in range (0, n):
        if (arr[i] == x):
            return i
    return -1
 
# 在数组 arr 中查找字符 D
arr = [ 'A', 'B', 'C', 'D', 'E' ]
x = input("请输入要查找的元素：")
n = len(arr)
result = search(arr, n, x)
if(result == -1):
    print("元素不在数组中")
else:
    print("元素在数组中的索引为", result)

Keputusan berjalan:

Sila masukkan elemen yang anda ingin cari: A
Indeks elemen dalam tatasusunan ialah 0

Sila masukkan elemen yang anda ingin cari: a
Elemen tiada dalam tatasusunan

Isih

Isih sisipan

Isih sisipan (Isih Sisipan): ialah algoritma pengisihan yang mudah dan intuitif. Ia berfungsi dengan membina urutan tersusun Untuk data yang tidak diisih, ia mengimbas dari belakang ke hadapan dalam urutan yang diisih, mencari kedudukan yang sepadan dan memasukkannya.

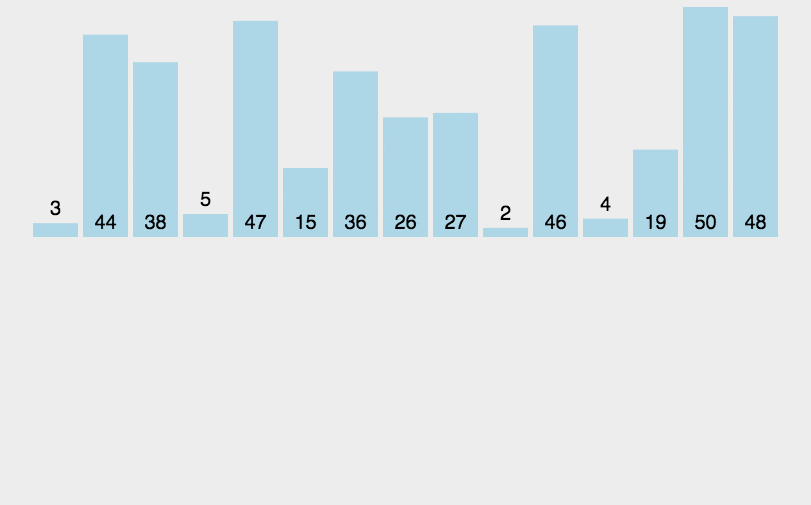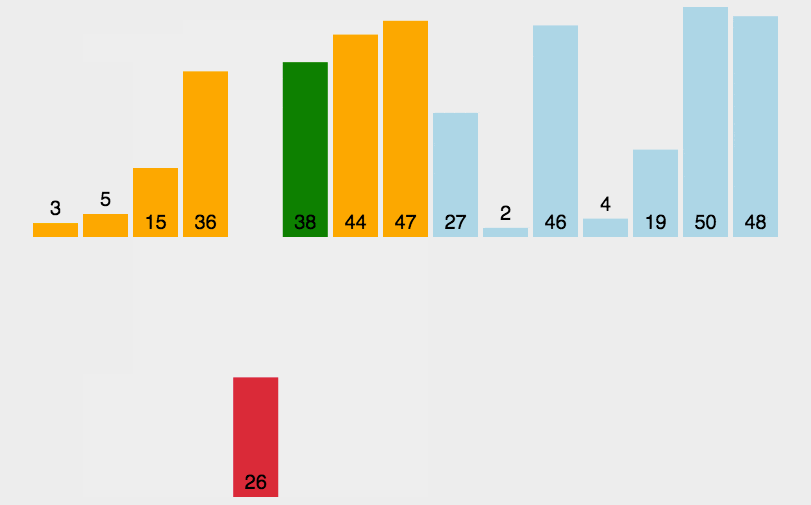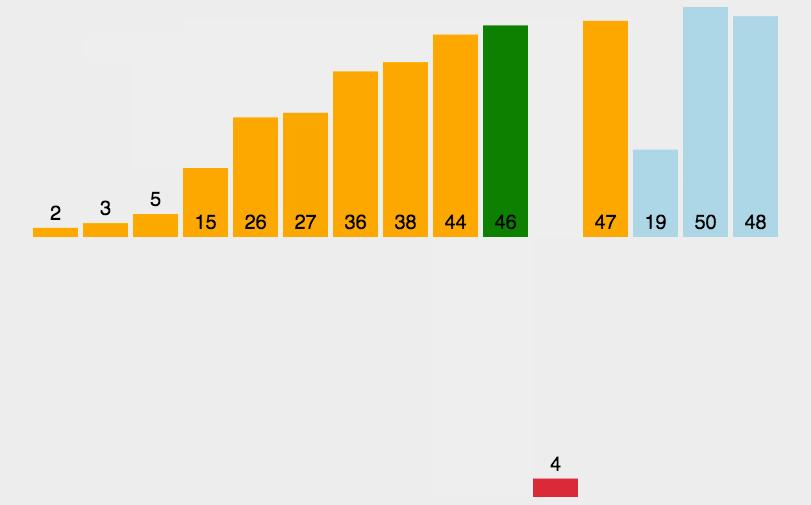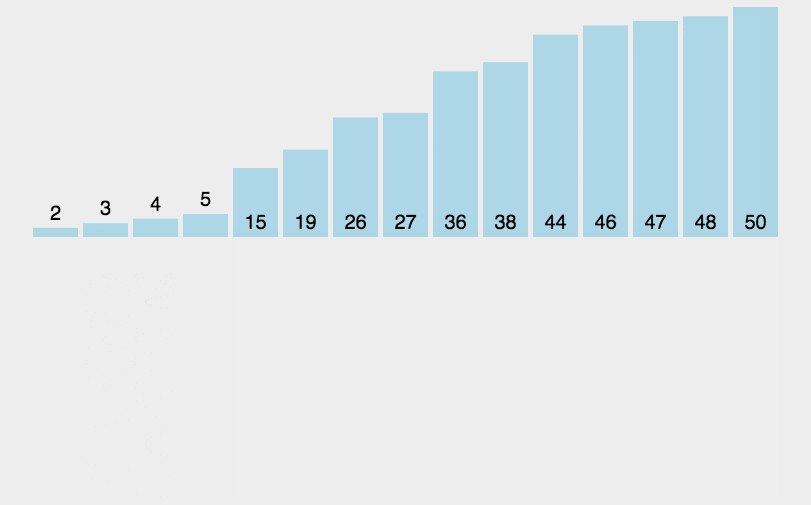
def insertionSort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >= 0 and key < arr[j]:
                arr[j+1] = arr[j]
                j -= 1
        arr[j+1] = key
 
arr = [12, 11, 13, 5, 6, 7, 9, 9, 17]
insertionSort(arr)
print("排序后的数组:")
print(arr)

Hasil jalankan:

Tatasusunan disusun:
[5, 6, 7, 9, 9 , 11, 12, 13, 17]

Sudah tentu boleh juga ditulis begini, yang lebih ringkas

list1 = [12, 11, 13, 5, 6, 7, 9, 9, 17]
for i in range(len(list1)-1, 0, -1):
    for j in range(0, i):
        if list1[i] < list1[j]:
            list1[i], list1[j] = list1[j], list1[i]
print(list1)

Isih cepat

Isih cepat;Gunakan strategi bahagi dan takluk untuk membahagikan urutan (senarai) kepada dua urutan, satu yang lebih kecil dan satu yang lebih besar, dan kemudian menyusun dua urutan secara rekursif.

Langkahnya ialah:

• Pilih nilai asas: Pilih elemen daripada jujukan, dipanggil "asas " (pivot);

• Split: Susun semula jujukan, semua elemen yang lebih kecil daripada nilai asas diletakkan di hadapan asas, dan semua elemen yang lebih besar daripada nilai asas diletakkan di hadapan pangkalan Di belakang pangkalan (nombor yang sama dengan nilai asas boleh pergi ke kedua-dua belah). Selepas pembahagian ini selesai, pengisihan nilai rujukan telah selesai

• Isih urutan secara rekursif: Isih urutan secara rekursif dengan elemen kurang daripada nilai rujukan dan lebih besar daripada Susunan Susunan unsur nilai asas.

Syarat penghakiman untuk mengulang ke bawah ialah saiz jujukan adalah sifar atau satu Pada masa ini, urutan itu jelas teratur.

Terdapat beberapa kaedah khusus untuk memilih nilai penanda aras Kaedah pemilihan ini mempunyai kesan yang menentukan pada prestasi masa pengisihan.

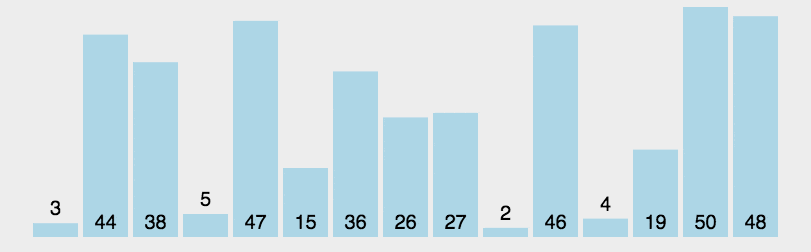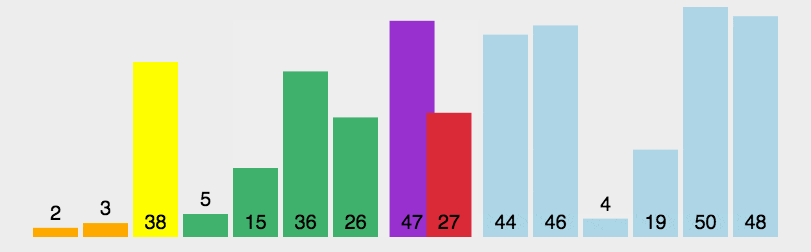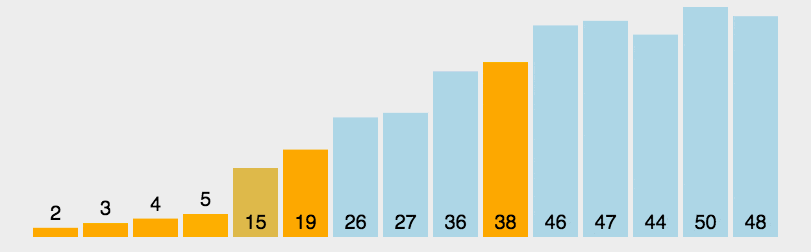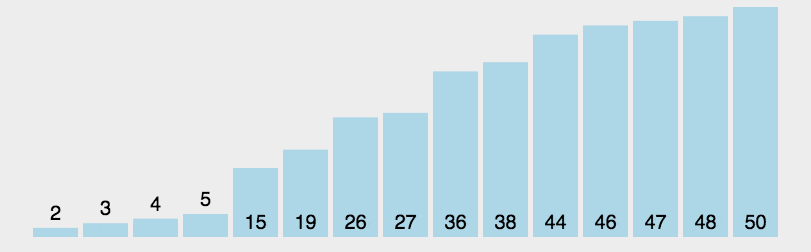
def partition(arr, low, high):
    i = (low-1)         # 最小元素索引
    pivot = arr[high]
 
    for j in range(low, high):
        # 当前元素小于或等于 pivot
        if arr[j] <= pivot:
            i = i+1
            arr[i], arr[j] = arr[j], arr[i]
 
    arr[i+1], arr[high] = arr[high], arr[i+1]
    return (i+1)
 
# arr[] --> 排序数组
# low  --> 起始索引
# high  --> 结束索引
 
# 快速排序函数
def quickSort(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quickSort(arr, low, pi-1)
        quickSort(arr, pi+1, high)
    return arr
 
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
 
print("排序后的数组:")
print(quickSort(arr, 0, n-1))

Keputusan berjalan:

Susun atur diisih:
[1, 5, 7, 8 , 9 , 10]

Isih pilihan

Isih pilihan: ialah algoritma pengisihan yang mudah dan intuitif. Begini cara ia berfungsi.

Mula-mula cari elemen terkecil (besar) dalam jujukan yang tidak diisih dan simpannya pada permulaan jujukan yang diisih Kemudian, teruskan mencari elemen terkecil (besar) daripada unsur-unsur yang tidak diisih yang tinggal dan masukkannya ke dalam urutan tersusun. Dan seterusnya sehingga semua elemen disusun.

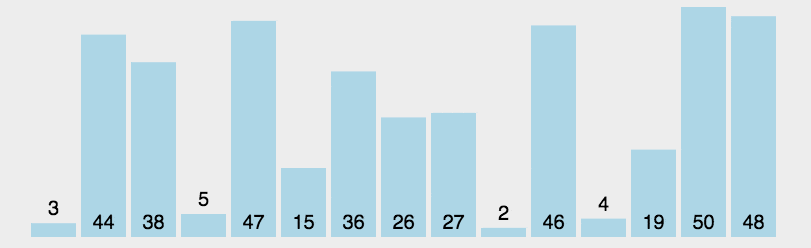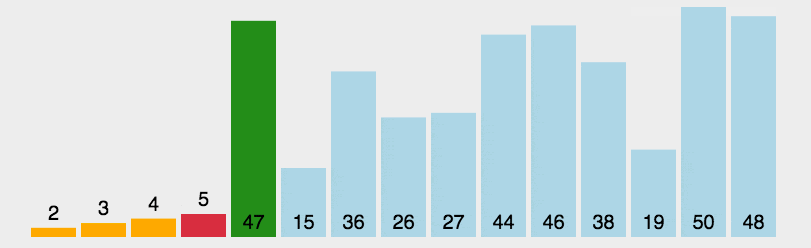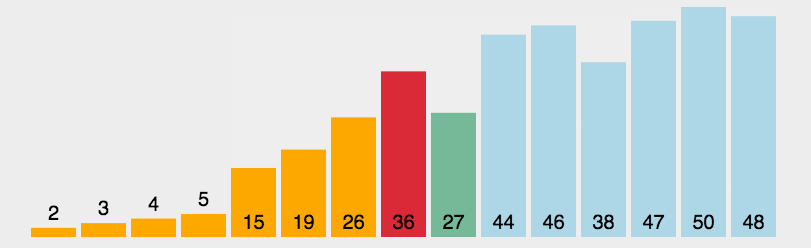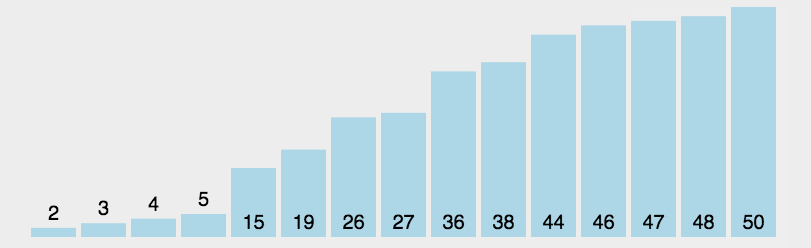
A = [64, 25, 12, 22, 11]
for i in range(len(A)): 
    min_idx = i
    for j in range(i+1, len(A)):
        if A[min_idx] > A[j]:
            min_idx = j
 
    A[i], A[min_idx] = A[min_idx], A[i]
 
print("排序后的数组：")
print(A)

Hasil jalankan:

Tatasusunan diisih:
[11, 12, 22, 25, 64 ]

Isih Buih

Isih Buih: juga merupakan algoritma pengisihan yang mudah dan intuitif. Ia berulang kali berjalan melalui urutan untuk diisih, membandingkan dua elemen pada satu masa dan menukarnya jika ia berada dalam susunan yang salah. Kerja melawat tatasusunan diulang sehingga tiada lagi pertukaran diperlukan, yang bermaksud tatasusunan telah diisih. Nama algoritma ini berasal dari fakta bahawa elemen yang lebih kecil akan perlahan-lahan "terapung" ke bahagian atas tatasusunan melalui pertukaran.

def bubbleSort(arr):
    n = len(arr)
    # 遍历所有数组元素
    for i in range(n):
        # Last i elements are already in place
        for j in range(0, n-i-1):
 
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr
 
arr = [64, 34, 25, 12, 22, 11, 90]
 
print("排序后的数组:")
print(bubbleSort(arr))

Hasil jalankan:

Tatasusunan disusun:
[11, 12, 22, 25, 34 , 64, 90]

归并排序

归并排序（Merge sort，或mergesort）：，是创建在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

分治法:

• 分割：递归地把当前序列平均分割成两半。

• 集成：在保持元素顺序的同时将上一步得到的子序列集成到一起（归并）。

def merge(arr, l, m, r):
    n1 = m - l + 1
    n2 = r - m
 
    # 创建临时数组
    L = [0] * (n1)
    R = [0] * (n2)
 
    # 拷贝数据到临时数组 arrays L[] 和 R[]
    for i in range(0, n1):
        L[i] = arr[l + i]
 
    for j in range(0, n2):
        R[j] = arr[m + 1 + j]
 
    # 归并临时数组到 arr[l..r]
    i = 0     # 初始化第一个子数组的索引
    j = 0     # 初始化第二个子数组的索引
    k = l     # 初始归并子数组的索引
 
    while i < n1 and j < n2:
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1
 
    # 拷贝 L[] 的保留元素
    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1
 
    # 拷贝 R[] 的保留元素
    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1
 
def mergeSort(arr, l, r):
    if l < r:
        m = int((l+(r-1))/2)
        mergeSort(arr, l, m)
        mergeSort(arr, m+1, r)
        merge(arr, l, m, r)
    return arr
 
print ("给定的数组")
arr = [12, 11, 13, 5, 6, 7, 13]
print(arr)
n = len(arr)
mergeSort(arr, 0, n-1)
print("排序后的数组")
print(arr)

运行结果：

给定的数组
[12, 11, 13, 5, 6, 7, 13]
排序后的数组
[5, 6, 7, 11, 12, 13, 13]

堆排序

堆排序（Heapsort）：是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2
    if l < n and arr[i] < arr[l]:
        largest = l
    if r < n and arr[largest] < arr[r]:
        largest = r
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 交换
def heapSort(arr):
    n = len(arr)
    # Build a maxheap.
    for i in range(n, -1, -1):
        heapify(arr, n, i)
    # 一个个交换元素
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]   # 交换
        heapify(arr, i, 0)
    return arr
arr = [12, 11, 13, 5, 6, 7, 13, 18]
heapSort(arr)
print("排序后的数组")
print(heapSort(arr))

运行结果：

排序后的数组
[5, 6, 7, 12, 11, 13, 13, 18]

计数排序

计数排序：的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

def countSort(arr):
    output = [0 for i in range(256)]
    count = [0 for i in range(256)]
    ans = ["" for _ in arr]
    for i in arr:
        count[ord(i)] += 1
    for i in range(256):
        count[i] += count[i-1] 
    for i in range(len(arr)):
        output[count[ord(arr[i])]-1] = arr[i]
        count[ord(arr[i])] -= 1
    for i in range(len(arr)):
        ans[i] = output[i]
    return ans
arr = "wwwnowcodercom"
ans = countSort(arr)
print("字符数组排序 %s" %("".join(ans)))

运行结果：

字符数组排序 ccdemnooorwwww

希尔排序

希尔排序：也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

def shellSort(arr):
    n = len(arr)
    gap = int(n/2)
 
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j-gap] > temp:
                arr[j] = arr[j-gap]
                j -= gap
            arr[j] = temp
        gap = int(gap/2)
    return arr
 
arr = [12, 34, 54, 2, 3, 2, 5]
 
print("排序前:")
print(arr)
print("排序后:")
print(shellSort(arr))

运行结果：

排序前:
[12, 34, 54, 2, 3, 2, 5]
排序后:
[2, 2, 3, 5, 12, 34, 54]

拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。拓扑排序是一种将集合上的偏序转换为全序的操作。

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（英语：Topological sorting）：

每个顶点出现且只出现一次；若A在序列中排在B的前面，则在图中不存在从B到A的路径。

from collections import defaultdict
class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)
        self.V = vertices
    def addEdge(self, u, v):
        self.graph[u].append(v)
    def topologicalSortUtil(self, v, visited, stack):
 
        visited[v] = True
 
        for i in self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        stack.insert(0,v)
    def topologicalSort(self):
        visited = [False]*self.V
        stack = []
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        print(stack)
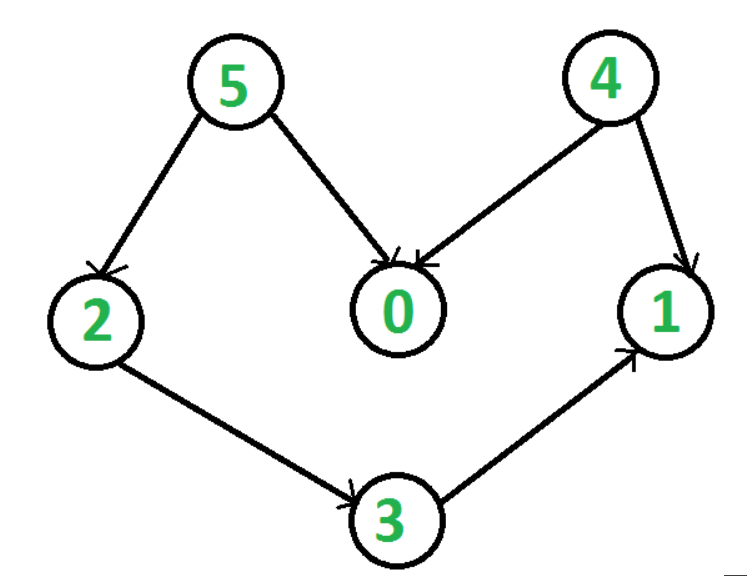
g= Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print("拓扑排序结果：")
g.topologicalSort()

运行结果：   

拓扑排序结果：
[5, 4, 2, 3, 1, 0]

Atas ialah kandungan terperinci Analisis kod contoh algoritma carian dan pengisihan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!