Bagaimana untuk memanggil dan melaksanakan kaedah kuasa dua terkecil dalam Python

Kaedah kuasa dua terkecil linear boleh difahami sebagai kesinambungan penyelesaian persamaan Perbezaannya ialah apabila kuantiti yang tidak diketahui jauh lebih kecil daripada bilangan persamaan, masalah yang tidak boleh diselesaikan akan diperolehi. Intipati kaedah kuasa dua terkecil adalah untuk memberikan nilai kepada nombor yang tidak diketahui sambil memastikan ralat minimum.

Kaedah kuasa dua terkecil ialah algoritma yang sangat klasik dan kami telah didedahkan kepada nama ini di sekolah menengah, dan ia merupakan algoritma yang sangat biasa digunakan. Saya sebelum ini telah menulis tentang prinsip kuasa dua terkecil linear dan melaksanakannya dalam Python: kuasa dua terkecil dan pelaksanaan Pythonnya dan cara memanggil kuasa dua terkecil tak linear dalam scipy: kuasa dua terkecil tak linear (Kandungan tambahan pada akhir artikel) ;Terdapat juga kaedah kuasa dua terkecil bagi matriks jarang: kaedah kuasa dua terkecil matriks jarang.

Berikut menerangkan kaedah kuasa dua terkecil linear yang dilaksanakan dalam numpy dan scipy, dan membandingkan kelajuan kedua-duanya.

pelaksanaan numpy

Kaedah kuasa dua terkecil dilaksanakan dalam numpy, iaitu, lstsq(a,b) digunakan untuk menyelesaikan x serupa dengan a@x=b, dengan a ialah M× N matriks; maka apabila b ialah vektor bagi baris M, ia hanya setara dengan menyelesaikan sistem persamaan linear. Untuk sistem persamaan seperti Ax=b, jika A ialah simulasi peringkat penuh, ia boleh dinyatakan sebagai x=A^&tolak;1b, jika tidak, ia boleh dinyatakan sebagai x=(A^TA )^&tolak;1A^Tb.

Apabila b ialah matriks M×K, maka bagi setiap lajur, set x akan dikira.

Terdapat 4 nilai pulangan, iaitu x yang diperoleh dengan pemasangan, ralat pemasangan, pangkat matriks a, dan bentuk nilai tunggal bagi matriks a.

import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]

pakej scipy

scipy.linalg juga menyediakan fungsi kuasa dua terkecil, nama fungsi juga lstsq, dan senarai parameternya ialah

lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

di mana a, b ialah Ax = b. Kedua-duanya menyediakan suis yang boleh dibatalkan Menetapkannya kepada Benar boleh menjimatkan masa berjalan Selain itu, fungsi ini juga menyokong semakan keterbatasan, yang merupakan pilihan yang ada pada banyak fungsi. Nilai pulangannya adalah sama dengan fungsi kuasa dua terkecil dalam numpy.

cond ialah parameter titik terapung, menunjukkan ambang nilai tunggal Apabila nilai tunggal kurang daripada cond, ia akan dibuang.

lapack_driver ialah pilihan rentetan, yang menunjukkan enjin algoritma dalam LAPACK dipilih, secara pilihan 'gelsd', 'gelsy', 'gelss'.

import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]

Perbandingan kelajuan

Akhir sekali, buat perbandingan kelajuan antara dua set fungsi kuasa dua terkecil

from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807

Kali ini, kedua-duanya tidak terlalu jauh Perbezaannya ialah walaupun dimensi matriks dibesarkan kepada 500, kedua-duanya adalah lebih kurang sama.

N = 500
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173

Tambahan

Python memanggil kaedah kuasa dua terkecil tak linear

Pengenalan dan pembina

In In scipy , tujuan kaedah kuasa dua terkecil tak linear adalah untuk mencari set fungsi yang meminimumkan jumlah kuasa dua fungsi ralat, yang boleh dinyatakan sebagai formula berikut

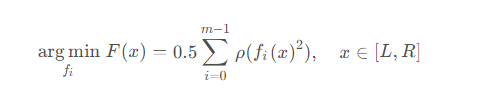
di mana ρ mewakili fungsi kehilangan , boleh difahami sebagai prapemprosesan f_i(x).

scipy.optimize merangkum fungsi kuasa dua terkecil tak linear least_squares, yang ditakrifkan sebagai

least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs)

Antaranya, func dan x0 adalah parameter yang diperlukan, func ialah fungsi yang perlu diselesaikan, dan x0 ialah input fungsi Nilai awal , tiada nilai lalai untuk kedua-dua parameter ini, ia adalah parameter yang mesti dimasukkan.

terikat ialah selang penyelesaian, lalainya ialah (&tolak;∞,∞). Di samping itu, parameter berikut digunakan untuk mengawal ralat, yang agak mudah.

< tr>

Nilai lalai

Catatan

ftol

10

	默认值	备注
ftol	10-8	函数容忍度
xtol	10-8	自变量容忍度
gtol	10-8	梯度容忍度
x_scale	1.0	变量的特征尺度
f_scale	1.0	残差边际值

-8<🎜>

Toleransi fungsi

xtol

10<🎜>-8<🎜>

Toleransi pembolehubah bebas

gtol

10<🎜> -8 <🎜>

Toleransi kecerunan

x_scale

1.0

Skala ciri pembolehubah

f_scale

1.0

Nilai margin baki

loss为损失函数，就是上面公式中的ρ \rhoρ，默认为linear，可选值包括

迭代策略

上面的公式仅给出了算法的目的，但并未暴露其细节。关于如何找到最小值，则需要确定搜索最小值的方法，method为最小值搜索的方案，共有三种选项，默认为trf

• trf：即Trust Region Reflective，信赖域反射算法

• dogbox：信赖域狗腿算法

• lm：Levenberg-Marquardt算法

这三种方法都是信赖域方法的延申，信赖域的优化思想其实就是从单点的迭代变成了区间的迭代，由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数，故而仅对其原理做简略的介绍。

其中r为置信半径，假设在这个邻域内，目标函数可以近似为线性或二次函数，则可通过二次模型得到区间中的极小值点s_k。然后以这个极小值点为中心，继续优化信赖域所对应的区间。

雅可比矩阵

在了解了信赖域方法之后，就会明白雅可比矩阵在数值求解时的重要作用，而如何计算雅可比矩阵，则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法，主要提供了三种方案，分别是基于两点的2-point；基于三点的3-point；以及基于复数步长的cs。一般来说，三点的精度高于两点，但速度也慢一倍。

此外，可以输入自定义函数来计算雅可比矩阵。

测试

最后，测试一下非线性最小二乘法

import numpy as np
from scipy.optimize import least_squares

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
    return _sum

x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
'''
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
'''

Atas ialah kandungan terperinci Bagaimana untuk memanggil dan melaksanakan kaedah kuasa dua terkecil dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!