Walaupun objek dalam dunia objektif adalah tiga dimensi, imej yang kami perolehi adalah dua dimensi, tetapi kita boleh Maklumat tiga dimensi sasaran dikesan dalam imej dua dimensi ini. Teknologi pembinaan semula tiga dimensi memproses imej dengan cara tertentu untuk mendapatkan maklumat tiga dimensi yang boleh dikenali oleh komputer, dengan itu menganalisis sasaran. Pembinaan semula 3D monokular mensimulasikan penglihatan binokular berdasarkan pergerakan kamera tunggal untuk mendapatkan maklumat visual tiga dimensi objek di angkasa, di mana monokular merujuk kepada satu kamera.
Dalam proses pembinaan semula objek 3D bermata, persekitaran operasi yang berkaitan adalah seperti berikut:
termasuk Langkah berikut: (1) Penentukuran kamera (2) Pengekstrakan ciri imej dan pemadanan (3) Pembinaan semula tiga dimensi Seterusnya , kita Mari kita lihat secara terperinci pelaksanaan khusus setiap langkah: (1) Penentukuran kamera Terdapat banyak kamera dalam kehidupan seharian kita, seperti kamera pada telefon mudah alih, kamera digital dan jenis modul berfungsi, dsb. Parameter setiap kamera adalah berbeza, iaitu, resolusi, mod, dsb. foto yang diambil oleh kamera. Dengan mengandaikan bahawa apabila kita melakukan pembinaan semula tiga dimensi objek, kita tidak mengetahui parameter matriks kamera kita terlebih dahulu, maka kita harus mengira parameter matriks kamera. Langkah ini dipanggil penentukuran kamera. Saya tidak akan memperkenalkan prinsip penentukuran kamera yang berkaitan Ramai orang di Internet telah menerangkannya secara terperinci. Pelaksanaan khusus penentukuran adalah seperti berikut:matplotlib 3.3.4
utamanya>
numpy 1.19.5
opencv-contrib-python 3.4.2.16
opencv-python 3.4.2.16
bantal 8.2.0
python 3.6.2
def camera_calibration(ImagePath):
# 循环中断
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 棋盘格尺寸（棋盘格的交叉点的个数）
row = 11
column = 8
objpoint = np.zeros((row * column, 3), np.float32)
objpoint[:, :2] = np.mgrid[0:row, 0:column].T.reshape(-1, 2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
batch_images = glob.glob(ImagePath + '/*.jpg')
for i, fname in enumerate(batch_images):
img = cv2.imread(batch_images[i])
imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# find chess board corners
ret, corners = cv2.findChessboardCorners(imgGray, (row, column), None)
# if found, add object points, image points (after refining them)
if ret:
objpoints.append(objpoint)
corners2 = cv2.cornerSubPix(imgGray, corners, (11, 11), (-1, -1), criteria)
imgpoints.append(corners2)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (row, column), corners2, ret)
cv2.imwrite('Checkerboard_Image/Temp_JPG/Temp_' + str(i) + '.jpg', img)
print("成功提取:", len(batch_images), "张图片角点！")
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, imgGray.shape[::-1], None, None)
Antara algoritma pengekstrakan titik ciri imej, terdapat tiga algoritma yang biasa digunakan, iaitu: algoritma SIFT, algoritma SURF dan algoritma ORB. Melalui analisis dan perbandingan yang komprehensif, kami menggunakan algoritma SURF untuk mengekstrak titik ciri imej dalam langkah ini. Jika anda berminat untuk membandingkan kesan pengekstrakan titik ciri bagi tiga algoritma, anda boleh mencari dalam talian dan lihat saya tidak akan membandingkannya satu per satu di sini. Pelaksanaan khusus adalah seperti berikut:
def epipolar_geometric(Images_Path, K):
IMG = glob.glob(Images_Path)
img1, img2 = cv2.imread(IMG[0]), cv2.imread(IMG[1])
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# Initiate SURF detector
SURF = cv2.xfeatures2d_SURF.create()
# compute keypoint & descriptions
keypoint1, descriptor1 = SURF.detectAndCompute(img1_gray, None)
keypoint2, descriptor2 = SURF.detectAndCompute(img2_gray, None)
print("角点数量：", len(keypoint1), len(keypoint2))
# Find point matches
bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
matches = bf.match(descriptor1, descriptor2)
print("匹配点数量：", len(matches))
src_pts = np.asarray([keypoint1[m.queryIdx].pt for m in matches])
dst_pts = np.asarray([keypoint2[m.trainIdx].pt for m in matches])
# plot
knn_image = cv2.drawMatches(img1_gray, keypoint1, img2_gray, keypoint2, matches[:-1], None, flags=2)
image_ = Image.fromarray(np.uint8(knn_image))
image_.save("MatchesImage.jpg")
# Constrain matches to fit homography
retval, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 100.0)
# We select only inlier points
points1 = src_pts[mask.ravel() == 1]
points2 = dst_pts[mask.ravel() == 1]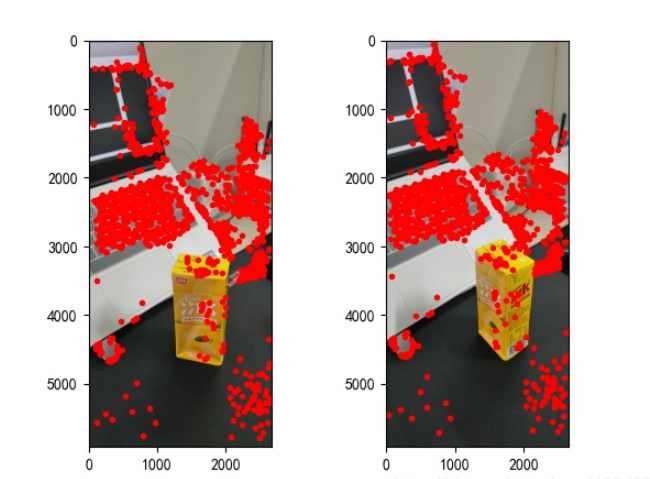
points1 = cart2hom(points1.T)
points2 = cart2hom(points2.T)
# plot
fig, ax = plt.subplots(1, 2)
ax[0].autoscale_view('tight')
ax[0].imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB))
ax[0].plot(points1[0], points1[1], 'r.')
ax[1].autoscale_view('tight')
ax[1].imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB))
ax[1].plot(points2[0], points2[1], 'r.')
plt.savefig('MatchesPoints.jpg')
fig.show()
#
points1n = np.dot(np.linalg.inv(K), points1)
points2n = np.dot(np.linalg.inv(K), points2)
E = compute_essential_normalized(points1n, points2n)
print('Computed essential matrix:', (-E / E[0][1]))
P1 = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2s = compute_P_from_essential(E)
ind = -1
for i, P2 in enumerate(P2s):
# Find the correct camera parameters
d1 = reconstruct_one_point(points1n[:, 0], points2n[:, 0], P1, P2)
# Convert P2 from camera view to world view
P2_homogenous = np.linalg.inv(np.vstack([P2, [0, 0, 0, 1]]))
d2 = np.dot(P2_homogenous[:3, :4], d1)
if d1[2] > 0 and d2[2] > 0:
ind = i
P2 = np.linalg.inv(np.vstack([P2s[ind], [0, 0, 0, 1]]))[:3, :4]
Points3D = linear_triangulation(points1n, points2n, P1, P2)
fig = plt.figure()
fig.suptitle('3D reconstructed', fontsize=16)
ax = fig.gca(projection='3d')
ax.plot(Points3D[0], Points3D[1], Points3D[2], 'b.')
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.view_init(elev=135, azim=90)
plt.savefig('Reconstruction.jpg')
plt.show()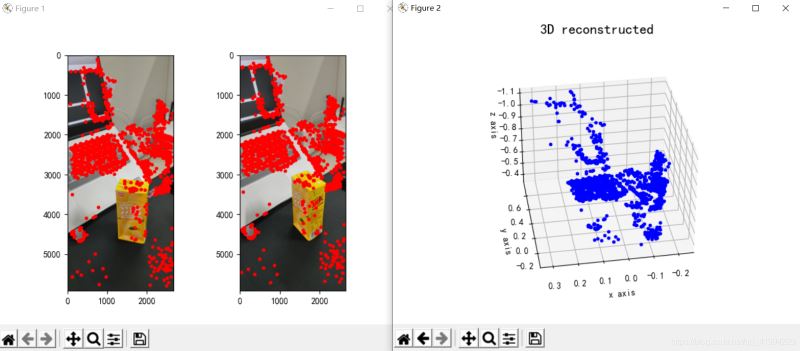
(2) Persekitaran sekeliling apabila gangguan menangkap gambar. Adalah lebih baik untuk memilih satu lokasi penangkapan untuk mengurangkan gangguan daripada objek yang tidak berkaitan; Lokasi foto yang dipilih mesti memastikan kecerahan yang sesuai (anda perlu menguji situasi khusus untuk mengetahui sama ada sumber cahaya anda memenuhi standard), dan apabila menggerakkan kamera, anda juga mesti memastikan bahawa sumber cahaya adalah konsisten antara detik sebelumnya dan ini. seketika.
Malah, prestasi pembinaan semula 3D monokular biasanya lemah Walaupun semua keadaan optimum, kesan pembinaan semula yang terhasil tidak begitu baik. Atau kita boleh pertimbangkan untuk menggunakan pembinaan semula binokular 3D Kesan pembinaan semula binokular adalah lebih baik daripada kesan monokular. Sebenarnya, operasinya tidak rumit Bahagian yang paling menyusahkan ialah merakam dan menentukur kedua-dua kamera itu agak mudah.
4. Kod
import cv2
import json
import numpy as np
import glob
from PIL import Image
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def cart2hom(arr):
""" Convert catesian to homogenous points by appending a row of 1s
:param arr: array of shape (num_dimension x num_points)
:returns: array of shape ((num_dimension+1) x num_points)
"""
if arr.ndim == 1:
return np.hstack([arr, 1])
return np.asarray(np.vstack([arr, np.ones(arr.shape[1])]))
def compute_P_from_essential(E):
""" Compute the second camera matrix (assuming P1 = [I 0])
from an essential matrix. E = [t]R
:returns: list of 4 possible camera matrices.
"""
U, S, V = np.linalg.svd(E)
# Ensure rotation matrix are right-handed with positive determinant
if np.linalg.det(np.dot(U, V)) < 0:
V = -V
# create 4 possible camera matrices (Hartley p 258)
W = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
P2s = [np.vstack((np.dot(U, np.dot(W, V)).T, U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W, V)).T, -U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W.T, V)).T, U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W.T, V)).T, -U[:, 2])).T]
return P2s
def correspondence_matrix(p1, p2):
p1x, p1y = p1[:2]
p2x, p2y = p2[:2]
return np.array([
p1x * p2x, p1x * p2y, p1x,
p1y * p2x, p1y * p2y, p1y,
p2x, p2y, np.ones(len(p1x))
]).T
return np.array([
p2x * p1x, p2x * p1y, p2x,
p2y * p1x, p2y * p1y, p2y,
p1x, p1y, np.ones(len(p1x))
]).T
def scale_and_translate_points(points):
""" Scale and translate image points so that centroid of the points
are at the origin and avg distance to the origin is equal to sqrt(2).
:param points: array of homogenous point (3 x n)
:returns: array of same input shape and its normalization matrix
"""
x = points[0]
y = points[1]
center = points.mean(axis=1) # mean of each row
cx = x - center[0] # center the points
cy = y - center[1]
dist = np.sqrt(np.power(cx, 2) + np.power(cy, 2))
scale = np.sqrt(2) / dist.mean()
norm3d = np.array([
[scale, 0, -scale * center[0]],
[0, scale, -scale * center[1]],
[0, 0, 1]
])
return np.dot(norm3d, points), norm3d
def compute_image_to_image_matrix(x1, x2, compute_essential=False):
""" Compute the fundamental or essential matrix from corresponding points
(x1, x2 3*n arrays) using the 8 point algorithm.
Each row in the A matrix below is constructed as
[x'*x, x'*y, x', y'*x, y'*y, y', x, y, 1]
"""
A = correspondence_matrix(x1, x2)
# compute linear least square solution
U, S, V = np.linalg.svd(A)
F = V[-1].reshape(3, 3)
# constrain F. Make rank 2 by zeroing out last singular value
U, S, V = np.linalg.svd(F)
S[-1] = 0
if compute_essential:
S = [1, 1, 0] # Force rank 2 and equal eigenvalues
F = np.dot(U, np.dot(np.diag(S), V))
return F
def compute_normalized_image_to_image_matrix(p1, p2, compute_essential=False):
""" Computes the fundamental or essential matrix from corresponding points
using the normalized 8 point algorithm.
:input p1, p2: corresponding points with shape 3 x n
:returns: fundamental or essential matrix with shape 3 x 3
"""
n = p1.shape[1]
if p2.shape[1] != n:
raise ValueError('Number of points do not match.')
# preprocess image coordinates
p1n, T1 = scale_and_translate_points(p1)
p2n, T2 = scale_and_translate_points(p2)
# compute F or E with the coordinates
F = compute_image_to_image_matrix(p1n, p2n, compute_essential)
# reverse preprocessing of coordinates
# We know that P1' E P2 = 0
F = np.dot(T1.T, np.dot(F, T2))
return F / F[2, 2]
def compute_fundamental_normalized(p1, p2):
return compute_normalized_image_to_image_matrix(p1, p2)
def compute_essential_normalized(p1, p2):
return compute_normalized_image_to_image_matrix(p1, p2, compute_essential=True)
def skew(x):
""" Create a skew symmetric matrix *A* from a 3d vector *x*.
Property: np.cross(A, v) == np.dot(x, v)
:param x: 3d vector
:returns: 3 x 3 skew symmetric matrix from *x*
"""
return np.array([
[0, -x[2], x[1]],
[x[2], 0, -x[0]],
[-x[1], x[0], 0]
])
def reconstruct_one_point(pt1, pt2, m1, m2):
"""
pt1 and m1 * X are parallel and cross product = 0
pt1 x m1 * X = pt2 x m2 * X = 0
"""
A = np.vstack([
np.dot(skew(pt1), m1),
np.dot(skew(pt2), m2)
])
U, S, V = np.linalg.svd(A)
P = np.ravel(V[-1, :4])
return P / P[3]
def linear_triangulation(p1, p2, m1, m2):
"""
Linear triangulation (Hartley ch 12.2 pg 312) to find the 3D point X
where p1 = m1 * X and p2 = m2 * X. Solve AX = 0.
:param p1, p2: 2D points in homo. or catesian coordinates. Shape (3 x n)
:param m1, m2: Camera matrices associated with p1 and p2. Shape (3 x 4)
:returns: 4 x n homogenous 3d triangulated points
"""
num_points = p1.shape[1]
res = np.ones((4, num_points))
for i in range(num_points):
A = np.asarray([
(p1[0, i] * m1[2, :] - m1[0, :]),
(p1[1, i] * m1[2, :] - m1[1, :]),
(p2[0, i] * m2[2, :] - m2[0, :]),
(p2[1, i] * m2[2, :] - m2[1, :])
])
_, _, V = np.linalg.svd(A)
X = V[-1, :4]
res[:, i] = X / X[3]
return res
def writetofile(dict, path):
for index, item in enumerate(dict):
dict[item] = np.array(dict[item])
dict[item] = dict[item].tolist()
js = json.dumps(dict)
with open(path, 'w') as f:
f.write(js)
print("参数已成功保存到文件")
def readfromfile(path):
with open(path, 'r') as f:
js = f.read()
mydict = json.loads(js)
print("参数读取成功")
return mydict
def camera_calibration(SaveParamPath, ImagePath):
# 循环中断
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 棋盘格尺寸
row = 11
column = 8
objpoint = np.zeros((row * column, 3), np.float32)
objpoint[:, :2] = np.mgrid[0:row, 0:column].T.reshape(-1, 2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
batch_images = glob.glob(ImagePath + '/*.jpg')
for i, fname in enumerate(batch_images):
img = cv2.imread(batch_images[i])
imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# find chess board corners
ret, corners = cv2.findChessboardCorners(imgGray, (row, column), None)
# if found, add object points, image points (after refining them)
if ret:
objpoints.append(objpoint)
corners2 = cv2.cornerSubPix(imgGray, corners, (11, 11), (-1, -1), criteria)
imgpoints.append(corners2)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (row, column), corners2, ret)
cv2.imwrite('Checkerboard_Image/Temp_JPG/Temp_' + str(i) + '.jpg', img)
print("成功提取:", len(batch_images), "张图片角点！")
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, imgGray.shape[::-1], None, None)
dict = {'ret': ret, 'mtx': mtx, 'dist': dist, 'rvecs': rvecs, 'tvecs': tvecs}
writetofile(dict, SaveParamPath)
meanError = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)
meanError += error
print("total error: ", meanError / len(objpoints))
def epipolar_geometric(Images_Path, K):
IMG = glob.glob(Images_Path)
img1, img2 = cv2.imread(IMG[0]), cv2.imread(IMG[1])
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# Initiate SURF detector
SURF = cv2.xfeatures2d_SURF.create()
# compute keypoint & descriptions
keypoint1, descriptor1 = SURF.detectAndCompute(img1_gray, None)
keypoint2, descriptor2 = SURF.detectAndCompute(img2_gray, None)
print("角点数量：", len(keypoint1), len(keypoint2))
# Find point matches
bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
matches = bf.match(descriptor1, descriptor2)
print("匹配点数量：", len(matches))
src_pts = np.asarray([keypoint1[m.queryIdx].pt for m in matches])
dst_pts = np.asarray([keypoint2[m.trainIdx].pt for m in matches])
# plot
knn_image = cv2.drawMatches(img1_gray, keypoint1, img2_gray, keypoint2, matches[:-1], None, flags=2)
image_ = Image.fromarray(np.uint8(knn_image))
image_.save("MatchesImage.jpg")
# Constrain matches to fit homography
retval, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 100.0)
# We select only inlier points
points1 = src_pts[mask.ravel() == 1]
points2 = dst_pts[mask.ravel() == 1]
points1 = cart2hom(points1.T)
points2 = cart2hom(points2.T)
# plot
fig, ax = plt.subplots(1, 2)
ax[0].autoscale_view('tight')
ax[0].imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB))
ax[0].plot(points1[0], points1[1], 'r.')
ax[1].autoscale_view('tight')
ax[1].imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB))
ax[1].plot(points2[0], points2[1], 'r.')
plt.savefig('MatchesPoints.jpg')
fig.show()
#
points1n = np.dot(np.linalg.inv(K), points1)
points2n = np.dot(np.linalg.inv(K), points2)
E = compute_essential_normalized(points1n, points2n)
print('Computed essential matrix:', (-E / E[0][1]))
P1 = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2s = compute_P_from_essential(E)
ind = -1
for i, P2 in enumerate(P2s):
# Find the correct camera parameters
d1 = reconstruct_one_point(points1n[:, 0], points2n[:, 0], P1, P2)
# Convert P2 from camera view to world view
P2_homogenous = np.linalg.inv(np.vstack([P2, [0, 0, 0, 1]]))
d2 = np.dot(P2_homogenous[:3, :4], d1)
if d1[2] > 0 and d2[2] > 0:
ind = i
P2 = np.linalg.inv(np.vstack([P2s[ind], [0, 0, 0, 1]]))[:3, :4]
Points3D = linear_triangulation(points1n, points2n, P1, P2)
return Points3D
def main():
CameraParam_Path = 'CameraParam.txt'
CheckerboardImage_Path = 'Checkerboard_Image'
Images_Path = 'SubstitutionCalibration_Image/*.jpg'
# 计算相机参数
camera_calibration(CameraParam_Path, CheckerboardImage_Path)
# 读取相机参数
config = readfromfile(CameraParam_Path)
K = np.array(config['mtx'])
# 计算3D点
Points3D = epipolar_geometric(Images_Path, K)
# 重建3D点
fig = plt.figure()
fig.suptitle('3D reconstructed', fontsize=16)
ax = fig.gca(projection='3d')
ax.plot(Points3D[0], Points3D[1], Points3D[2], 'b.')
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.view_init(elev=135, azim=90)
plt.savefig('Reconstruction.jpg')
plt.show()
if __name__ == '__main__':
main()Atas ialah kandungan terperinci Bagaimana untuk merealisasikan pembinaan semula 3D monokular berdasarkan python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
