 pembangunan bahagian belakang
pembangunan bahagian belakang
 Tutorial Python
Tutorial Python
 Bagaimana untuk melaksanakan gabungan jenis algoritma pengisihan python
Bagaimana untuk melaksanakan gabungan jenis algoritma pengisihan python
Bagaimana untuk melaksanakan gabungan jenis algoritma pengisihan python
Penerangan Algoritma
Algoritma pengisihan lanjutan pertama dalam bahagian ini ialah isihan gabungan. Perkataan "penggabungan" bermaksud "untuk bergabung". Seperti namanya, algoritma isihan cantuman ialah algoritma yang mula-mula membahagikan jujukan kepada sub-jujukan, mengisih sub-jujukan, dan kemudian menggabungkan sub-jujukan tersusun ke dalam urutan tertib yang lengkap. Ia sebenarnya mengamalkan idea bahagi dan takluk.
Purata kerumitan masa isihan gabungan ialah O(nlgn), kerumitan masa dalam kes terbaik ialah O(nlgn), dan kerumitan masa dalam kes terburuk juga O(nlgn). Kerumitan ruangnya ialah O(1). Selain itu, pengisihan gabungan ialah algoritma pengisihan yang stabil.
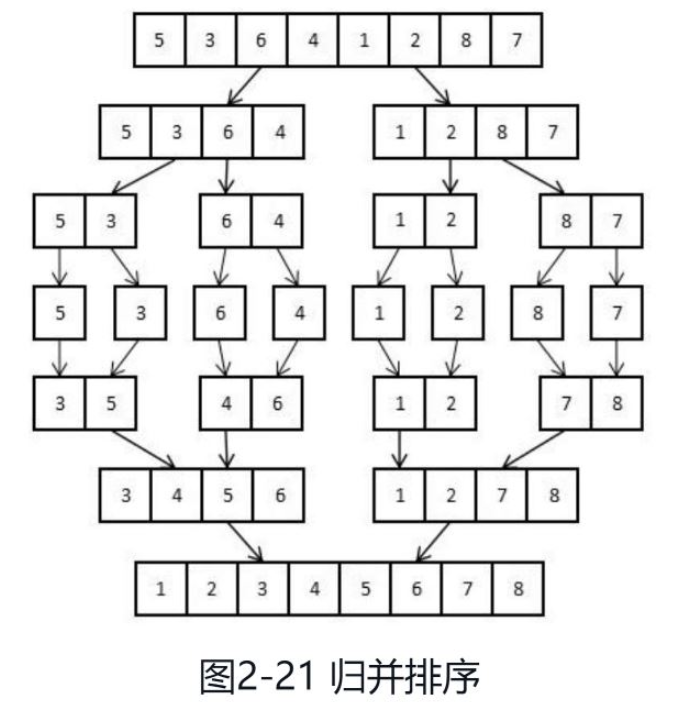
Mengambil isihan menaik sebagai contoh, proses algoritma cantuman ditunjukkan dalam Rajah 2-21.
Tatasusunan asal ialah tatasusunan tidak tertib 8 nombor. Selepas satu operasi, tatasusunan 8 nombor dibahagikan kepada dua tatasusunan tidak tertib 4 nombor. Setiap operasi membahagikan tatasusunan tidak tertib kepada separuh sehingga semua subarray terkecil mengandungi hanya satu elemen. Apabila terdapat hanya satu elemen dalam tatasusunan, tatasusunan mesti dipesan. Kemudian, program ini mula menggabungkan setiap dua tatasusunan tertib kecil ke dalam tatasusunan tertib yang besar. Mula-mula, gabungkan dua tatasusunan yang mengandungi satu nombor ke dalam tatasusunan yang mengandungi dua nombor, kemudian cantumkan dua tatasusunan yang mengandungi dua nombor ke dalam tatasusunan yang mengandungi empat nombor, dan akhirnya cantumkannya ke dalam tatasusunan yang mengandungi lapan nombor. Apabila semua tatasusunan tersusun digabungkan, tatasusunan terpanjang yang terbentuk akan diisih.
Pelaksanaan kod
Gabung kod isihan:
#归并排序
nums = [5,3,6,4,1,2,8,7]
def MergeSort(num):
if(len(num)<=1): #递归边界条件
return num #到达边界时返回当前的子数组
mid = int(len(num)/2) #求出数组的中位数
llist,rlist = MergeSort(num[:mid]),MergeSort(num[mid:])#调用函数分别为左右数组排序
result = []
i,j = 0,0
while i < len(llist) and j < len(rlist): #while循环用于合并两个有序数组
if rlist[j]<llist[i]:
result.append(rlist[j])
j += 1
else:
result.append(llist[i])
i += 1
result += llist[i:]+rlist[j:] #把数组未添加的部分加到结果数组末尾
return result #返回已排序的数组
print(MergeSort(nums))Jalankan program, hasil output ialah:
[1,2,3,4,5,6,7,8]
Dalam MergeSort Dalam fungsi (), langkah pertama adalah untuk menilai syarat sempadan. Apabila tatasusunan yang mengandungi hanya satu elemen diluluskan sebagai parameter fungsi, unsur itu sahaja wujud dalam tatasusunan, jadi tatasusunan telah mencapai saiz minimumnya. Sebaik sahaja anda selesai dengan tugas menguraikan tatasusunan secara rekursif, hanya kembalikan tatasusunan terurai ke tahap rekursi sebelumnya.
Jika panjang tatasusunan yang tidak diisih masih lebih besar daripada 1, maka gunakan pembolehubah pertengahan untuk menyimpan subskrip tengah tatasusunan dan bahagikan tatasusunan yang tidak diisih kepada dua subarray di sebelah kiri dan kanan. Kemudian, cipta dua tatasusunan baharu untuk menyimpan subarray kiri dan kanan yang diisih. Idea rekursi digunakan di sini. Kami hanya memikirkan fungsi MergeSort() sebagai fungsi yang mengisih senarai, walaupun di dalam fungsi MergeSort(), fungsi itu sendiri juga boleh dipanggil untuk mengisih dua subarray.
Kemudian, gunakan gelung sementara untuk menggabungkan dua tatasusunan yang telah diisih. Memandangkan saiz relatif elemen dalam dua tatasusunan tidak dapat ditentukan, kami menggunakan dua pembolehubah, i dan j, untuk menandakan kedudukan elemen yang menunggu untuk ditambah dalam sub-tatasusunan kiri dan sub-tatasusunan kanan masing-masing. Apabila gelung while tamat, mungkin terdapat beberapa elemen terbesar yang tinggal di penghujung subarray yang belum ditambahkan pada senarai hasil, jadi pernyataan result+=llist[i:]+rlist[j:] adalah untuk menghalang elemen ini daripada dirindui. Selepas penggabungan tatasusunan selesai, fungsi mengeluarkan tatasusunan tertib.
Atas ialah kandungan terperinci Bagaimana untuk melaksanakan gabungan jenis algoritma pengisihan python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 Bagaimanakah Feathering PS mengawal kelembutan peralihan?
Apr 06, 2025 pm 07:33 PM
Bagaimanakah Feathering PS mengawal kelembutan peralihan?
Apr 06, 2025 pm 07:33 PM
Kunci kawalan bulu adalah memahami sifatnya secara beransur -ansur. PS sendiri tidak menyediakan pilihan untuk mengawal lengkung kecerunan secara langsung, tetapi anda boleh melaraskan radius dan kelembutan kecerunan dengan pelbagai bulu, topeng yang sepadan, dan pilihan halus untuk mencapai kesan peralihan semula jadi.
 Cara Menggunakan MySQL Selepas Pemasangan
Apr 08, 2025 am 11:48 AM
Cara Menggunakan MySQL Selepas Pemasangan
Apr 08, 2025 am 11:48 AM
Artikel ini memperkenalkan operasi pangkalan data MySQL. Pertama, anda perlu memasang klien MySQL, seperti MySqlworkbench atau Command Line Client. 1. Gunakan perintah MySQL-Uroot-P untuk menyambung ke pelayan dan log masuk dengan kata laluan akaun root; 2. Gunakan CreateTatabase untuk membuat pangkalan data, dan gunakan Pilih pangkalan data; 3. Gunakan createtable untuk membuat jadual, menentukan medan dan jenis data; 4. Gunakan InsertInto untuk memasukkan data, data pertanyaan, kemas kini data dengan kemas kini, dan padam data dengan padam. Hanya dengan menguasai langkah -langkah ini, belajar menangani masalah biasa dan mengoptimumkan prestasi pangkalan data anda boleh menggunakan MySQL dengan cekap.
 Adakah Mysql perlu membayar
Apr 08, 2025 pm 05:36 PM
Adakah Mysql perlu membayar
Apr 08, 2025 pm 05:36 PM
MySQL mempunyai versi komuniti percuma dan versi perusahaan berbayar. Versi komuniti boleh digunakan dan diubahsuai secara percuma, tetapi sokongannya terhad dan sesuai untuk aplikasi dengan keperluan kestabilan yang rendah dan keupayaan teknikal yang kuat. Edisi Enterprise menyediakan sokongan komersil yang komprehensif untuk aplikasi yang memerlukan pangkalan data yang stabil, boleh dipercayai, berprestasi tinggi dan bersedia membayar sokongan. Faktor yang dipertimbangkan apabila memilih versi termasuk kritikal aplikasi, belanjawan, dan kemahiran teknikal. Tidak ada pilihan yang sempurna, hanya pilihan yang paling sesuai, dan anda perlu memilih dengan teliti mengikut keadaan tertentu.
 Bagaimana cara menyediakan bulu ps?
Apr 06, 2025 pm 07:36 PM
Bagaimana cara menyediakan bulu ps?
Apr 06, 2025 pm 07:36 PM
PS Feathering adalah kesan kabur tepi imej, yang dicapai dengan purata piksel berwajaran di kawasan tepi. Menetapkan jejari bulu dapat mengawal tahap kabur, dan semakin besar nilai, semakin kaburnya. Pelarasan fleksibel radius dapat mengoptimumkan kesan mengikut imej dan keperluan. Sebagai contoh, menggunakan jejari yang lebih kecil untuk mengekalkan butiran apabila memproses foto watak, dan menggunakan radius yang lebih besar untuk mewujudkan perasaan kabur ketika memproses karya seni. Walau bagaimanapun, perlu diperhatikan bahawa terlalu besar jejari boleh dengan mudah kehilangan butiran kelebihan, dan terlalu kecil kesannya tidak akan jelas. Kesan bulu dipengaruhi oleh resolusi imej dan perlu diselaraskan mengikut pemahaman imej dan kesan genggaman.
 Apakah kesan PS Feathering pada kualiti imej?
Apr 06, 2025 pm 07:21 PM
Apakah kesan PS Feathering pada kualiti imej?
Apr 06, 2025 pm 07:21 PM
PS Feathering boleh menyebabkan kehilangan butiran imej, ketepuan warna yang dikurangkan dan peningkatan bunyi. Untuk mengurangkan kesan, disarankan untuk menggunakan radius bulu yang lebih kecil, menyalin lapisan dan kemudian bulu, dan berhati -hati membandingkan kualiti imej sebelum dan selepas bulu. Di samping itu, bulu tidak sesuai untuk semua kes, dan kadang -kadang alat seperti topeng lebih sesuai untuk mengendalikan tepi imej.
 Cara mengoptimumkan prestasi pangkalan data selepas pemasangan MySQL
Apr 08, 2025 am 11:36 AM
Cara mengoptimumkan prestasi pangkalan data selepas pemasangan MySQL
Apr 08, 2025 am 11:36 AM
Pengoptimuman prestasi MySQL perlu bermula dari tiga aspek: konfigurasi pemasangan, pengindeksan dan pengoptimuman pertanyaan, pemantauan dan penalaan. 1. Selepas pemasangan, anda perlu menyesuaikan fail my.cnf mengikut konfigurasi pelayan, seperti parameter innodb_buffer_pool_size, dan tutup query_cache_size; 2. Buat indeks yang sesuai untuk mengelakkan indeks yang berlebihan, dan mengoptimumkan pernyataan pertanyaan, seperti menggunakan perintah menjelaskan untuk menganalisis pelan pelaksanaan; 3. Gunakan alat pemantauan MySQL sendiri (ShowProcessList, ShowStatus) untuk memantau kesihatan pangkalan data, dan kerap membuat semula dan mengatur pangkalan data. Hanya dengan terus mengoptimumkan langkah -langkah ini, prestasi pangkalan data MySQL diperbaiki.
 Bagaimana untuk mengoptimumkan prestasi MySQL untuk aplikasi beban tinggi?
Apr 08, 2025 pm 06:03 PM
Bagaimana untuk mengoptimumkan prestasi MySQL untuk aplikasi beban tinggi?
Apr 08, 2025 pm 06:03 PM
Panduan Pengoptimuman Prestasi Pangkalan Data MySQL Dalam aplikasi yang berintensifkan sumber, pangkalan data MySQL memainkan peranan penting dan bertanggungjawab untuk menguruskan urus niaga besar-besaran. Walau bagaimanapun, apabila skala aplikasi berkembang, kemunculan prestasi pangkalan data sering menjadi kekangan. Artikel ini akan meneroka satu siri strategi pengoptimuman prestasi MySQL yang berkesan untuk memastikan aplikasi anda tetap cekap dan responsif di bawah beban tinggi. Kami akan menggabungkan kes-kes sebenar untuk menerangkan teknologi utama yang mendalam seperti pengindeksan, pengoptimuman pertanyaan, reka bentuk pangkalan data dan caching. 1. Reka bentuk seni bina pangkalan data dan seni bina pangkalan data yang dioptimumkan adalah asas pengoptimuman prestasi MySQL. Berikut adalah beberapa prinsip teras: Memilih jenis data yang betul dan memilih jenis data terkecil yang memenuhi keperluan bukan sahaja dapat menjimatkan ruang penyimpanan, tetapi juga meningkatkan kelajuan pemprosesan data.
 Penyelesaian ralat pemasangan mysql
Apr 08, 2025 am 10:48 AM
Penyelesaian ralat pemasangan mysql
Apr 08, 2025 am 10:48 AM
Alasan dan penyelesaian yang sama untuk kegagalan pemasangan MySQL: 1. Nama pengguna atau kata laluan yang tidak betul, atau perkhidmatan MySQL tidak dimulakan, anda perlu menyemak nama pengguna dan kata laluan dan memulakan perkhidmatan; 2. Konflik pelabuhan, anda perlu menukar pelabuhan pendengaran MySQL atau menutup program yang menduduki port 3306; 3. Perpustakaan Ketergantungan hilang, anda perlu menggunakan Pengurus Pakej Sistem untuk memasang perpustakaan ketergantungan yang diperlukan; 4. Kebenaran yang tidak mencukupi, anda perlu menggunakan hak sudo atau pentadbir untuk menjalankan pemasang; 5. Fail konfigurasi yang salah, anda perlu menyemak fail konfigurasi My.cnf untuk memastikan konfigurasi adalah betul. Hanya dengan bekerja dengan mantap dan teliti boleh mysql dipasang dengan lancar.



