Bagaimana untuk menggunakan @cache dalam Python

Apakah kegunaan hebat @cache dalam Python?

Dengan mengguna pakai strategi caching, ruang boleh ditukar kepada masa, dengan itu meningkatkan prestasi sistem komputer. Peranan caching dalam kod adalah untuk mengoptimumkan kelajuan berjalan kod, walaupun ia akan meningkatkan jejak memori.

Dalam functools modul terbina dalam Python, cache() fungsi tertib tinggi disediakan untuk melaksanakan caching, yang digunakan sebagai penghias: @cache.

Pengenalan fungsi caching @cache

Dalam kod sumber cache, perihalan cache ialah: Cache tanpa had ringan yang ringkas Kadang-kadang dipanggil "memoize Diterjemahkan ke dalam bahasa Cina: Cache tanpa had ringan yang ringkas. Hadkan caching. Kadang-kadang dipanggil "memoization".

def cache(user_function, /):
    'Simple lightweight unbounded cache.  Sometimes called "memoize".'
    return lru_cache(maxsize=None)(user_function)

cache() hanya mempunyai satu baris kod, memanggil fungsi lru_cache() dan menghantar parameter maxsize=None. lru_cache() juga merupakan fungsi dalam modul functools Semak kod sumber lru_cache() Nilai lalai maxsize ialah 128, yang bermaksud bahawa data cache maksimum ialah 128. Jika data melebihi 128, ia akan dipadamkan mengikut. kepada data LRU (Paling Lama Tidak Digunakan). cache() menetapkan saiz maksimum kepada Tiada, maka ciri LRU dinyahdayakan dan bilangan cache boleh berkembang tanpa had, jadi ia dipanggil "cache tidak terhad".

lru_cache() menggunakan algoritma LRU (Paling Tidak Digunakan Baru-baru ini), yang sudah lama tidak digunakan Inilah sebabnya terdapat tiga huruf lru dalam nama fungsi. Mekanisme algoritma yang paling kurang digunakan ialah dengan mengandaikan data tidak diakses dalam tempoh baru-baru ini, kemungkinan ia diakses pada masa hadapan juga sangat kecil Algoritma LRU memilih untuk menghapuskan data yang paling kurang digunakan baru-baru ini dan mengekalkannya data yang kerap digunakan.

cache() baharu dalam Python 3.9, lru_cache() baharu dalam Python 3.2, cache() membatalkan had bilangan cache berdasarkan lru_cache(), sebenarnya Ia berkaitan dengan kemajuan teknologi dan peningkatan ketara prestasi perkakasan cache() dan lru_cache() hanyalah versi berbeza bagi fungsi yang sama.

lru_cache() pada asasnya ialah penghias yang menyediakan fungsi caching untuk fungsi Ia menyimpan cache kumpulan bersaiz maksimum parameter masuk dan secara langsung mengembalikan hasil sebelumnya apabila fungsi dipanggil dengan parameter yang sama pada kali berikutnya. untuk menjimatkan wang. Masa panggilan untuk overhed tinggi atau fungsi I/O tinggi.

Senario aplikasi @cache

Cache mempunyai pelbagai senario aplikasi, seperti caching kandungan web statik Anda boleh terus menambah penghias @cache pada fungsi tempat pengguna akses laman web statik.

Dalam sesetengah kod rekursif, parameter yang sama dihantar berulang kali untuk melaksanakan kod fungsi Menggunakan cache boleh mengelakkan pengiraan berulang dan mengurangkan kerumitan masa kod.

Seterusnya, saya akan menggunakan jujukan Fibonacci sebagai contoh untuk menggambarkan peranan @cache Jika anda masih mempunyai sedikit pemahaman mengenainya selepas membaca kandungan sebelumnya, saya percaya anda akan mendapat pencerahan selepas membaca contoh tersebut .

Jujukan Fibonacci merujuk kepada urutan nombor: 1, 1, 2, 3, 5, 8, 13, 21, 34,..., bermula dari nombor ketiga, setiap nombor ialah Jumlah dua nombor pertama. Kebanyakan pemula mempunyai kod bertulis untuk urutan Fibonacci Perlaksanaannya tidak sukar Dalam Python, kodnya sangat ringkas. Seperti berikut:

def feibo(n):
    # 第0个数和第1个数为1
    a, b = 1, 1
    for _ in range(n):
        # 将b赋值给a,将a+b赋值给b,循环n次
        a, b = b, a+b
    return a

Sudah tentu, terdapat banyak cara untuk melaksanakan jujukan Fibonacci (sekurang-kurangnya lima atau enam untuk menggambarkan senario aplikasi @cache, artikel ini menggunakan kaedah rekursif untuk menulis Fibonacci). kod urutan. Seperti berikut:

def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    # 根据斐波那契数列的定义，其他情况递归返回前两个数之和
    return feibo_recur(n-1) + feibo_recur(n-2)

Apabila kod rekursif dilaksanakan, ia akan mengulang sehingga ke feibo_recur(1) dan feibo_recur(0), seperti yang ditunjukkan dalam rajah di bawah (mengambil nombor keenam sebagai contoh).

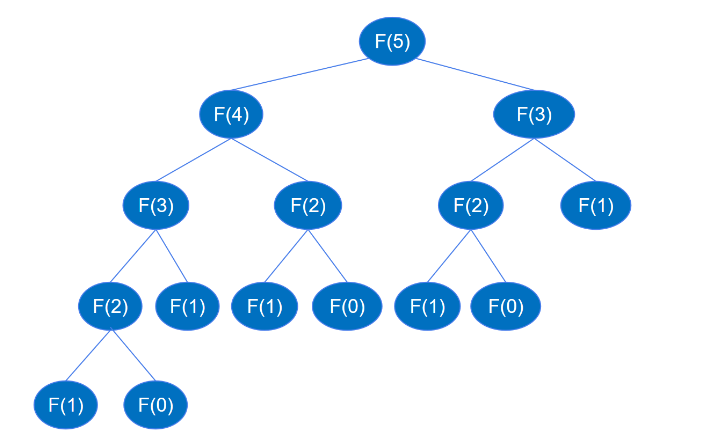
Apabila mencari F(5), anda mesti mencari F(4) dan F(3 dahulu apabila mencari F(4), anda mesti mencari F(3 dahulu ) dan F( 2), … Secara analogi, proses rekursif adalah serupa dengan proses lintasan kedalaman-pertama bagi pokok binari. Adalah diketahui bahawa pokok binari dengan ketinggian k boleh mempunyai sehingga 2k-1 nod Menurut rajah panggilan rekursif di atas, ketinggian pokok binari ialah n dan nod paling banyak 2n-1 panggilan fungsi rekursif adalah paling banyak 2n-1 kali , jadi kerumitan masa rekursi ialah O(2^n).

Apabila kerumitan masa ialah O(2^n), masa pelaksanaan berubah dengan sangat keterlaluan apabila n meningkat.

import time
for i in [10, 20, 30, 40]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

Nombor Fibonacci ke-10: 89
n=10 Masa Kos: 0.0
Nombor Fibonacci ke-20: 10946
n=20 Masa Kos: 0.0015988349914550781
Nombor Fibonacci ke-30: 1346269
n=30 Masa Kos: 0.17051291465759277
Nombor Fibonacci ke-40: 1645 ke-40: 20.90010976791382

Ia dapat dilihat dari masa larian bahawa apabila n adalah sangat kecil, masa larian adalah sangat cepat Apabila n meningkat, masa larian meningkat dengan cepat, terutamanya apabila n secara beransur-ansur meningkat kepada 30 dan 40, masa larian berubah dengan ketara. Bagi melihat corak perubahan masa dengan lebih jelas, ujian lanjut telah dijalankan.

for i in [41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

Nombor Fibonacci ke-41: 267914296

n=41 Masa Kos: 33.77224683761597
Nombor Fibonacci ke-4: 4 42 Kos Masa: 55.86398696899414
Nombor Fibonacci ke-43: 701408733
n=43 Masa Kos: 92.55108690261841

从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。

根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。

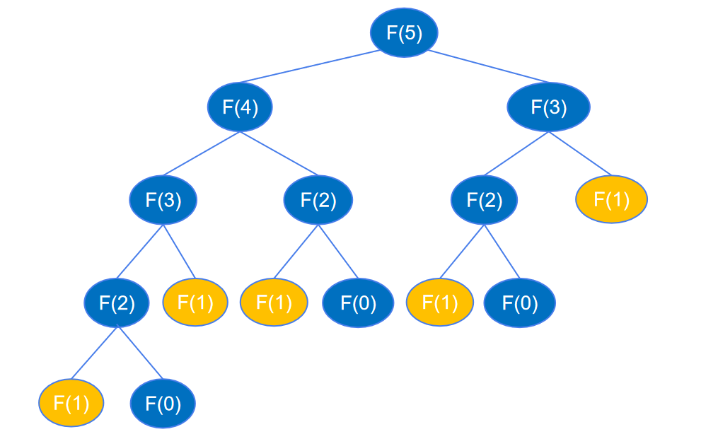
假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。

temp = {}  # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    if n in temp:  # 如果temp字典中有n,则直接返回值,不调用递归代码
        return temp[n]
    else:
        # 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
        temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
        return temp[n]

上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。

下面看一下代码的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)
print(temp)

Output:

第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}

可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。

上面的代码也可以用列表来当“备忘录”，代码如下。

temp = [1, 1]
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    if n < len(temp):
        return temp[n]
    else:
        # 第一次执行时，将结果保存到列表中，后续直接从列表中取
        temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
        return temp[n]

现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。

所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：

from functools import cache
@cache
def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    return feibo_recur(n-1) + feibo_recur(n-2)

使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0

完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。

补充：Python @cache装饰器

@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。

例：

@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
    print('开始计算a+b的值...')
    return a + b

可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。

Atas ialah kandungan terperinci Bagaimana untuk menggunakan @cache dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!