Bagaimana untuk melaksanakan algoritma klasifikasi pokok keputusan dalam python

Pra-maklumat

1. Pokok keputusan

Ayat yang ditulis semula: Dalam pembelajaran diselia, algoritma pengelasan yang biasa digunakan ialah pepohon keputusan, yang berdasarkan kumpulan sampel, setiap sampel mengandungi set atribut dan hasil pengelasan yang sepadan. Menggunakan sampel ini untuk pembelajaran, algoritma boleh menghasilkan pepohon keputusan yang boleh mengklasifikasikan data baharu dengan betul

2. Data sampel

Andaikan terdapat 14 pengguna sedia ada, dan atribut peribadi mereka Data pada sama ada untuk membeli produk tertentu adalah seperti berikut:

编号	年龄	收入范围	工作性质	信用评级	购买决策
01		高	不稳定	较差	否
02		高	不稳定	好	否
03	30-40	高	不稳定	较差	是
04	>40	中等	不稳定	较差	是
05	>40	低	稳定	较差	是
06	>40	低	稳定	好	否
07	30-40	低	稳定	好	是
08		中等	不稳定	较差	否
09		低	稳定	较差	是
10	>40	中等	稳定	较差	是
11		中等	稳定	好	是
12	30-40	中等	不稳定	好	是
13	30-40	高	稳定	较差	是
14	>40	中等	不稳定	好	否

Algoritma pengelasan pokok tertentu

1 Bina set data

Untuk memudahkan pemprosesan, data simulasi ditukar kepada data senarai berangka mengikut peraturan berikut:

Umur: < ;30 diberikan nilai 0; 30-40 diberikan nilai 1; ialah 2

Sifat kerja: tidak stabil 0; stabil ialah 1

Penilaian kredit: buruk ialah 0; baik ialah 1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,'N'],
            [0,2,0,1,'N'],
            [1,2,0,0,'Y'],
            [2,1,0,0,'Y'],
            [2,0,1,0,'Y'],
            [2,0,1,1,'N'],
            [1,0,1,1,'Y'],
            [0,1,0,0,'N'],
            [0,0,1,0,'Y'],
            [2,1,1,0,'Y'],
            [0,1,1,1,'Y'],
            [1,1,0,1,'Y'],
            [1,2,1,0,'Y'],
            [2,1,0,1,'N'],]
    labels=['age','income','job','credit']
    return dataSet,labels

Panggil fungsi untuk mendapatkan data:

ds1,lab = createdataset()
print(ds1)
print(lab)

[[0, 2 , 0, 0, ‘N’], [0, 2, 0, 1, ‘N’], [1, 2, 0, 0, ‘ Y’], [2, 1, 0, 0, ‘Y’], [2, 0, 1, 0, ‘Y’], [2, 0, 1, 1, ‘N’], [ 1, 0, 1, 1, ‘Y’] , [0, 1, 0, 0, ‘N’], [0, 0, 1, 0, ‘Y’], [2, 1, 1 , 0, ‘Y’], [0, 1 , 1, 1, ‘Y’], [1, 1, 0, 1, ‘Y’], [1, 2, 1, 0, ‘ Y’], [2, 1, 0, 1, ‘N’]]

[‘umur’, ‘pendapatan’, ‘pekerjaan’, ‘kredit’]

2. Entropi maklumat set data

Entropi maklumat, juga dikenali sebagai entropi Shannon, ialah jangkaan pembolehubah rawak. Mengukur tahap ketidakpastian maklumat. Semakin besar entropi maklumat, semakin sukar untuk mengetahui maklumat tersebut. Memproses maklumat adalah untuk menjelaskan maklumat, iaitu proses pengurangan entropi.

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

Contoh entropi maklumat data:

shan = calcShannonEnt(ds1)
print(shan)

0.9402859586706309

3 Kurangkan sumbangan set sampel X entropi. Lebih besar perolehan maklumat, lebih sesuai untuk mengelaskan X.

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

Kod di atas melaksanakan algoritma pembelajaran pokok keputusan ID3 berdasarkan perolehan entropi maklumat. Prinsip logik terasnya ialah: pilih setiap atribut dalam set atribut secara bergilir-gilir, dan bahagikan set sampel kepada beberapa subset mengikut nilai atribut ini, hitung entropi maklumat bagi subset ini, dan perbezaan antaranya dan entropi maklumat; sampel ialah Keuntungan entropi maklumat bagi pembahagian oleh atribut ini, cari atribut yang sepadan dengan keuntungan terbesar antara semua keuntungan, yang merupakan atribut yang digunakan untuk membahagikan set sampel.

Kira atribut sampel pecahan terbaik bagi sampel, dan hasilnya dipaparkan dalam lajur 0, iaitu atribut umur:

col = chooseBestFeatureToSplit(ds1)
col

0

4. Keputusan pembinaan Fungsi pokok

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

digunakan untuk mengendalikan situasi berikut: apabila pokok keputusan ideal akhir harus mencapai bahagian bawah di sepanjang cawangan keputusan, semua sampel harus mempunyai hasil pengelasan yang sama. Walau bagaimanapun, dalam sampel sebenar, tidak dapat dielakkan bahawa semua atribut adalah konsisten tetapi keputusan pengelasan adalah berbeza Dalam kes ini,

melaraskan label pengelasan sampel tersebut kepada hasil pengelasan dengan kejadian yang paling banyak.

majorityCnt ialah fungsi tugas teras, yang secara berurutan memanggil algoritma perolehan entropi maklumat ID3 untuk pemprosesan pengiraan pada semua atribut, dan akhirnya menghasilkan pepohon keputusan. majorityCnt

5. Bina pepohon keputusan melalui instantiasi

createTreeBina pepohon keputusan menggunakan data sampel:

Tree = createTree(ds1, lab)
print("样本数据决策树：")
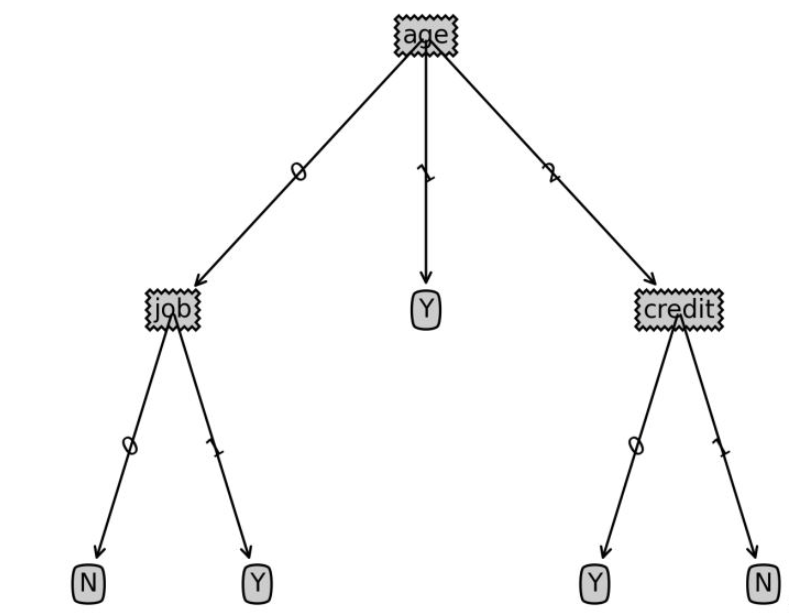
print(Tree)

Sampel pepohon keputusan data:

{‘umur&rsquo ;: {0: {‘pekerjaan’: {0: ‘N’, 1: ‘Y’}},

1: ‘Y’,

2: {‘kredit’: { 0: ‘Y’, 1: ‘N’}}}}

6 Pengkelasan sampel ujian

Berikan pengguna baharu Maklumat untuk menentukan sama ada dia akan membeli produk tertentu:

def classify(inputtree,featlabels,testvec):
    firststr = list(inputtree.keys())[0]
    seconddict = inputtree[firststr]
    featindex = featlabels.index(firststr)
    for key in seconddict.keys():
        if testvec[featindex]==key:
            if type(seconddict[key]).__name__=='dict':
                classlabel=classify(seconddict[key],featlabels,testvec)
            else:
                classlabel=seconddict[key]
    return classlabel

labels=['age','income','job','credit']
tsvec=[0,0,1,1]
print('result:',classify(Tree,labels,tsvec))
tsvec1=[0,2,0,1]
print('result1:',classify(Tree,labels,tsvec1))

hasil: Y

hasil1: N

年龄	收入范围	工作性质	信用评级
<30	低	稳定	好
<30	高	不稳定	好

Maklumat siaran: melukis pokok keputusan kod

Kod berikut digunakan untuk melukis grafik pepohon keputusan, bukan fokus algoritma pepohon keputusan Jika anda berminat, anda boleh merujuknya untuk mempelajari

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.savefig('决策树.png',dpi=300,bbox_inches='tight')
    plt.show()

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan algoritma klasifikasi pokok keputusan dalam python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!