Bagaimana untuk melaksanakan keluasan graf dan kedalaman algoritma carian laluan pertama dalam Python

Kata Pengantar

Graf ialah struktur data abstrak, yang pada asasnya sama dengan struktur pokok.

Berbanding dengan pokok, graf ditutup Struktur pokok boleh dianggap sebagai pendahulu struktur graf. Jika anda menggunakan sambungan mendatar antara nod adik beradik atau nod anak pada struktur pokok, anda boleh membuat struktur graf.

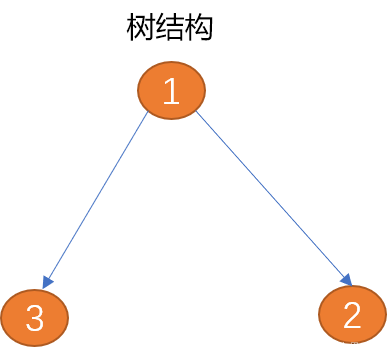
Tree sesuai untuk menerangkan struktur data satu-ke-banyak dari atas ke bawah, seperti struktur organisasi syarikat.

Graf sesuai untuk menerangkan struktur data banyak-ke-banyak yang lebih kompleks, seperti perhubungan sosial kumpulan yang kompleks.

1. Teori graf

Apabila menggunakan komputer untuk menyelesaikan masalah di dunia nyata, selain menyimpan data dalam maklumat dunia sebenar, dan juga perlu menerangkan dengan betul hubungan antara maklumat tersebut.

Sebagai contoh, semasa membangunkan atur cara peta, adalah perlu untuk mensimulasikan dengan betul hubungan antara bandar atau jalan raya di bandar pada komputer. Hanya atas dasar ini algoritma boleh digunakan untuk mengira laluan terbaik dari satu bandar ke bandar lain, atau dari titik permulaan yang ditentukan ke titik destinasi.

Begitu juga, terdapat peta laluan penerbangan, peta laluan kereta api dan peta komunikasi sosial.

Struktur graf secara berkesan boleh mencerminkan hubungan kompleks antara maklumat seperti yang diterangkan di atas dalam dunia nyata. Algoritma ini boleh digunakan untuk mengira laluan terpendek dengan mudah dalam laluan penerbangan, pelan pemindahan terbaik dalam laluan kereta api, siapa yang mempunyai hubungan terbaik dengan siapa dalam kalangan sosial dan siapa yang paling serasi dengan siapa dalam rangkaian perkahwinan. ..

1.1 Konsep graf

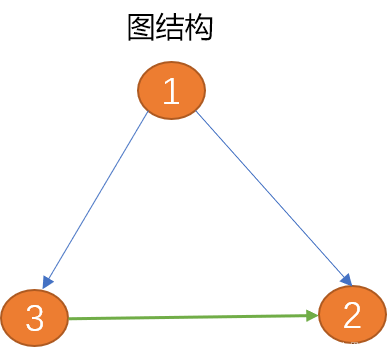
Puncak: Pucuk juga dipanggil nod, dan graf boleh dianggap sebagai himpunan bucu. Bucu itu sendiri mempunyai makna data, jadi bucu akan membawa maklumat tambahan, dipanggil "muatan".

Bucu boleh menjadi bandar, nama tempat, nama stesen, orang di dunia nyata...

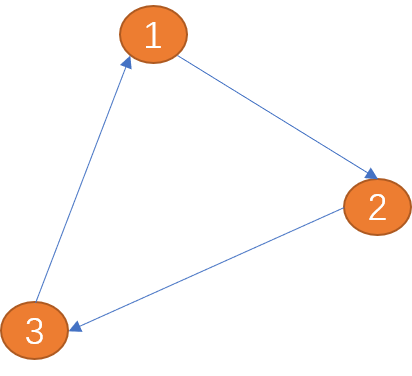
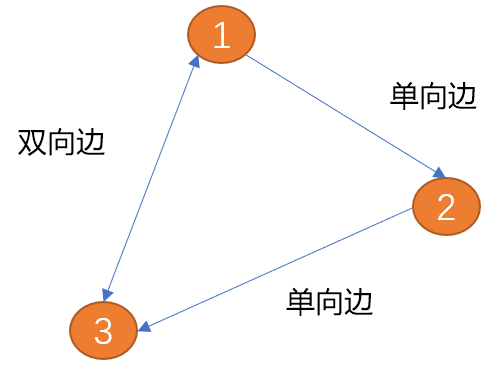
Tepi: dalam gambar Tepi digunakan untuk menerangkan hubungan antara bucu. Tepi boleh mempunyai arah atau tiada arah Tepi arah boleh dibahagikan kepada tepi satu arah dan tepi dua arah.

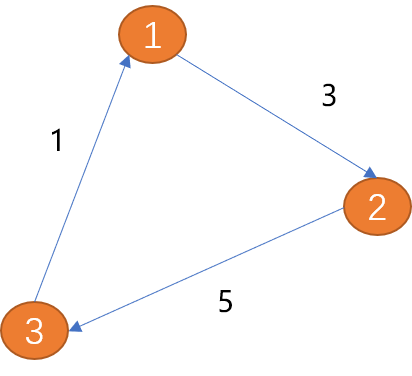
Tepi antara (titik 1) dan (bucu 2) dalam rajah di bawah hanya mempunyai satu arah (arah yang ditunjukkan oleh anak panah), dipanggil tepi sehala . Sama seperti jalan sehala di dunia nyata. Tepi antara

(bucu 1) dan (bucu 2) mempunyai dua arah (anak panah dua arah), dan dipanggil tepi dua arah. Hubungan antara bandar adalah kelebihan dua hala.

Berat: Maklumat nilai boleh ditambah pada tepi, dan nilai tambah dipanggil berat. Tepi berwajaran menerangkan kekuatan sambungan dari satu bucu ke bucu yang lain.

Sebagai contoh, dalam laluan kereta api bawah tanah sebenar, pemberat boleh menerangkan panjang masa, kilometer dan tambang antara dua stesen...

Tepi menerangkan hubungan antara bucu , berat menerangkan perbezaan hubungan.

Laluan:

Mula-mula faham konsep jalan di dunia nyata

Contohnya: Untuk memandu dari satu bandar ke bandar lain, anda perlu menentukan laluan terlebih dahulu. Itulah Bandar apa yang perlu anda lalui dari tempat berlepas ke destinasi? Berapa batu yang diperlukan?

Kita boleh katakan bahawa laluan ialah jujukan bucu yang disambungkan dengan tepi. Oleh kerana terdapat lebih daripada satu laluan, penerangan laluan dari satu titik item ke titik item lain tidak merujuk kepada satu jenis.

Bagaimana untuk mengira laluan dalam struktur graf?

• Panjang laluan tidak berwajaran ialah bilangan tepi pada laluan.

• Panjang laluan berwajaran ialah jumlah pemberat tepi pada laluan itu.

Seperti yang ditunjukkan di atas, panjang laluan dari (bucu 1) hingga (bucu 3) ialah 8.

Gelung: Bermula dari titik permulaan dan akhirnya kembali ke titik permulaan (titik akhir juga merupakan titik permulaan) akan membentuk gelung Gelung ialah laluan khas. Seperti di atas (V1, V2, V3, V1) ialah cincin.

Jenis gambar:

Ringkasnya, gambar boleh dibahagikan kepada kategori berikut:

• Graf terarah: Graf dengan tepi berarah dipanggil graf berarah.

• Graf tidak berarah: Graf yang tepinya tidak mempunyai arah dipanggil graf tidak berarah.

• Graf berwajaran: Graf dengan maklumat berat di tepinya dipanggil graf berwajaran.

• Graf asiklik: Graf tanpa kitaran dipanggil graf asiklik.

• Graf asiklik terarah: Graf terarah tanpa kitaran, dirujuk sebagai DAG.

1.2 Definisi graf

Mengikut ciri-ciri graf, struktur data graf mesti mengandungi sekurang-kurangnya dua jenis maklumat:

Semua bucu membentuk satu set maklumat, di sini diwakili oleh V (contohnya, dalam program peta, semua bandar dibentuk dalam set bucu).

Semua tepi membentuk maklumat yang ditetapkan, diwakili di sini oleh E (perihalan hubungan antara bandar).

Bagaimana untuk menerangkan tepi?

Tepi digunakan untuk mewakili hubungan antara titik item. Jadi kelebihan boleh merangkumi 3 metadata (titik mula, titik akhir, berat). Sudah tentu, pemberat boleh diabaikan, tetapi secara amnya apabila mengkaji graf, mereka merujuk kepada graf berwajaran.

Jika G digunakan untuk mewakili graf, maka G = (V, E). Setiap tepi boleh diterangkan dengan tuple (fv, ev) atau triplet （fv,ev,w）.

fv mewakili titik permulaan dan ev mewakili titik akhir. Dan fv, ev data mesti dirujuk dalam koleksi V.

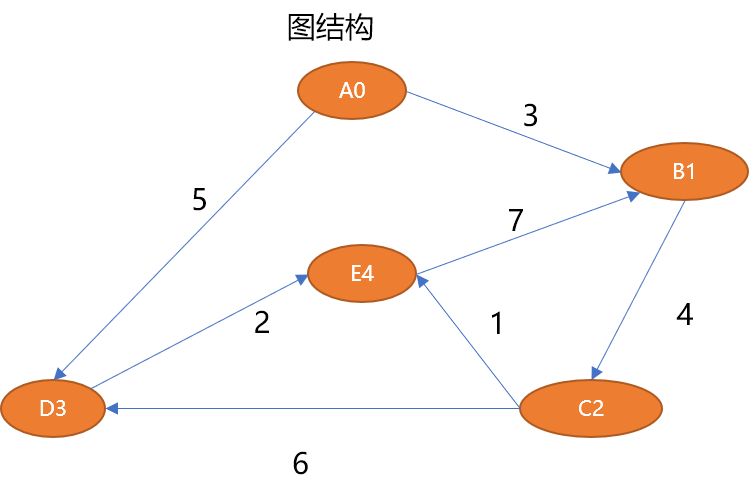
Struktur graf di atas boleh dihuraikan seperti berikut:

# 5 个顶点
V={A0,B1,C2,D3,E4}
# 7 条边
E={ (A0,B1,3),(B1,C2,4),(C2,D3,6),(C2,E4,1),(D3,E4,2),(A0,D3,5),(E4,B1,7)}

1.3 Struktur data abstrak graf

Penerangan data abstrak daripada graf mesti sekurang-kurangnya Beberapa kaedah:

• Graph ( ): Digunakan untuk mencipta gambar baharu.

• add_vertex( vert ): Tambahkan nod baharu pada graf, parameter hendaklah objek jenis nod.

• add_edge(fv，tv ): Wujudkan hubungan kelebihan antara 2 mata item.

• add_edge(fv，tv，w ): Wujudkan kelebihan antara 2 titik item dan nyatakan berat sambungan.

• find_vertex( key ): Cari bucu dalam graf berdasarkan kunci kata kunci.

• find_vertexs( ): Tanya semua maklumat bucu.

• find_path( fv,tv): Cari laluan dari satu bucu ke bucu yang lain.

2. Pelaksanaan storan graf

Terdapat dua pelaksanaan storan graf arus perdana: matriks bersebelahan dan senarai pautan.

2.1 Matriks bersebelahan

Gunakan matriks dua dimensi (tatasusunan) untuk menyimpan hubungan antara bucu.

Sebagai contoh, graph[5][5] boleh menyimpan data perhubungan 5 bucu Nombor baris dan nombor lajur mewakili bucu Nilai dalam sel yang bersilang dengan baris ke-v dan lajur ke-w tepi dari bucu v ke bucu w. Berat, seperti grap[2][3]=6 bermaksud bucu C2 dan bucu D3 bersambung (bersebelahan), beratnya ialah 6

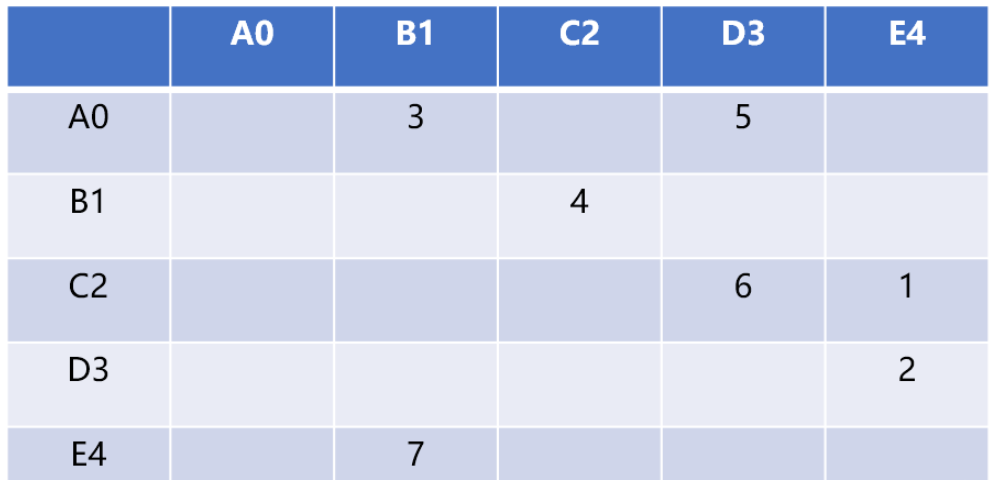
Kelebihan matriks bersebelahan ialah ia mudah dan boleh dinyatakan dengan jelas Bucu-bucu itu disambungkan. Oleh kerana tidak setiap pasangan bucu disambungkan, terdapat banyak ruang yang tidak digunakan dalam matriks, selalunya dipanggil "matriks jarang."

Matriks hanya akan diisi jika setiap bucu mempunyai hubungan dengan bucu lain. Jika hubungan antara struktur graf tidak terlalu kompleks, menggunakan struktur ini untuk menyimpan data graf akan membazirkan banyak ruang.

Matriks bersebelahan sesuai untuk mewakili struktur graf dengan hubungan yang kompleks, seperti pautan antara halaman web di Internet dan hubungan sosial antara orang dalam kalangan sosial...

2.2 Pengekodan ke implement adjacency Matrix

Oleh kerana bucu itu sendiri mempunyai makna data, jenis bucu perlu ditakrifkan terlebih dahulu.

Kelas bucu:

"""
节（顶）点类
"""
class Vertex:
    def __init__(self, name, v_id=0):
        # 顶点的编号
        self.v_id = v_id
        # 顶点的名称
        self.v_name = name
        # 是否被访问过:False 没有 True:有
        self.visited = False

    # 自我显示
    def __str__(self):
        return '[编号为 {0}，名称为 {1} ] 的顶点'.format(self.v_id, self.v_name)

Dalam kelas bucu, v_id dan v_name mudah difahami. Mengapa menambah visited?

Pembolehubah ini digunakan untuk merekodkan sama ada bucu telah dicari semasa proses carian laluan untuk mengelakkan pengiraan carian berulang.

Kelas graf: Kelas graf mempunyai banyak kaedah, di sini kami akan memperkenalkannya satu persatu.

Kaedah permulaan

class Graph:
    """
    nums:相邻矩阵的大小
    """

    def __init__(self, nums):
        # 一维列表，保存节点，最多只能有 nums 个节点
        self.vert_list = []
        # 二维列表，存储顶点及顶点间的关系(权重)
        # 初始权重为 0 ，表示节点与节点之间还没有建立起关系
        self.matrix = [[0] * nums for _ in range(nums)]
        # 顶点个数
        self.v_nums = 0
        # 使用队列模拟队列或栈，用于广度、深度优先搜索算法
        self.queue_stack = []
        # 保存搜索到的路径
        self.searchPath = []
        
    # 暂省略……

Kaedah permulaan digunakan untuk memulakan jenis data dalam graf:

Senarai satu dimensi vert_list Simpan semua data puncak.

Senarai dua dimensi matrix Menyimpan data perhubungan antara bucu.

queue_stack Gunakan senarai untuk mensimulasikan baris gilir atau tindanan untuk carian keluasan dan kedalaman berikutnya.

Bagaimana untuk menggunakan senarai untuk mensimulasikan baris gilir atau tindanan?

Senarai ini mempunyai 2 kaedah berharga: append() dan pop().

append() digunakan untuk menambah data pada senarai, dan setiap kali ia ditambahkan dari penghujung senarai.

pop() memadam dan memaparkan data dari penghujung senarai secara lalai, pop(参数) boleh memberikan nilai indeks untuk memadam dan meletuskan data dari kedudukan yang ditentukan.

Menggunakan kaedah append() dan pop() boleh mensimulasikan tindanan dan masuk dan keluar data dari tempat yang sama.

Gunakan kaedah append() dan pop(0) untuk mensimulasikan baris gilir, tambah data dari belakang dan dapatkan data dari hadapan

searchPath: Digunakan untuk menyimpan keluasan atau depth first path Keputusan dalam carian.

Tambah kaedah titik nod (puncak) baharu:

    """
    添加新顶点
    """
    def add_vertex(self, vert):
        if vert in self.vert_list:
            # 已经存在
            return
        if self.v_nums >= len(self.matrix):
            # 超过相邻矩阵所能存储的节点上限
            return
        # 顶点的编号内部生成
        vert.v_id = self.v_nums
        self.vert_list.append(vert)
        # 数量增一
        self.v_nums += 1

上述方法注意一点，节点的编号由图内部逻辑提供，便于节点编号顺序的统一。

添加边方法

此方法是邻接矩阵表示法的核心逻辑。

  '''
    添加节点与节点之间的边，
    如果是无权重图，统一设定为 1 
    '''
    def add_edge(self, from_v, to_v):
        # 如果节点不存在
        if from_v not in self.vert_list:
            self.add_vertex(from_v)
        if to_v not in self.vert_list:
            self.add_vertex(to_v)
        # from_v 节点的编号为行号，to_v 节点的编号为列号
        self.matrix[from_v.v_id][to_v.v_id] = 1

    '''
    添加有权重的边
    '''
    def add_edge(self, from_v, to_v, weight):
        # 如果节点不存在
        if from_v not in self.vert_list:
            self.add_vertex(from_v)
        if to_v not in self.vert_list:
            self.add_vertex(to_v)
        # from_v 节点的编号为行号，to_v 节点的编号为列号
        self.matrix[from_v.v_id][to_v.v_id] = weight

添加边信息的方法有 2 个，一个用来添加无权重边，一个用来添加有权重的边。

查找某节点

使用线性查找法从节点集合中查找某一个节点。

    '''
    根据节点编号返回节点
    '''
    def find_vertex(self, v_id):
        if v_id >= 0 or v_id <= self.v_nums:
            # 节点编号必须存在
            return [tmp_v for tmp_v in self.vert_list if tmp_v.v_id == v_id][0]

查询所有节点

  '''
    输出所有顶点信息
    '''
    def find_only_vertexes(self):
        for tmp_v in self.vert_list:
            print(tmp_v)

此方法仅为了查询方便。

查询节点之间的关系

    '''
    迭代节点与节点之间的关系（边）
    '''
    def find_vertexes(self):
        for tmp_v in self.vert_list:
            edges = self.matrix[tmp_v.v_id]
            for col in range(len(edges)):
                w = edges[col]
                if w != 0:
                    print(tmp_v, '和', self.vert_list[col], '的权重为：', w)

测试代码：

if __name__ == "__main__":
    # 初始化图对象
    g = Graph(5)
    # 添加顶点
    for _ in range(len(g.matrix)):
        v_name = input("顶点的名称（ q 为退出）：")
        if v_name == 'q':
            break
        v = Vertex(v_name)
        g.add_vertex(v)

    # 节点之间的关系
    infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
    for i in infos:
        v = g.find_vertex(i[0])
        v1 = g.find_vertex(i[1])
        g.add_edge(v, v1, i[2])
    # 输出顶点及边a
    print("-----------顶点与顶点关系--------------")
    g.find_vertexes()
    '''
    输出结果：
    顶点的名称（ q 为退出）：A
    顶点的名称（ q 为退出）：B
    顶点的名称（ q 为退出）：C
    顶点的名称（ q 为退出）：D
    顶点的名称（ q 为退出）：E
    [编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3
[编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5
[编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4
[编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6
[编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1
[编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2
[编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7
    '''

3. 搜索路径

在图中经常做的操作，就是查找从一个顶点到另一个顶点的路径。如怎么查找到 A0 到 E4 之间的路径长度：

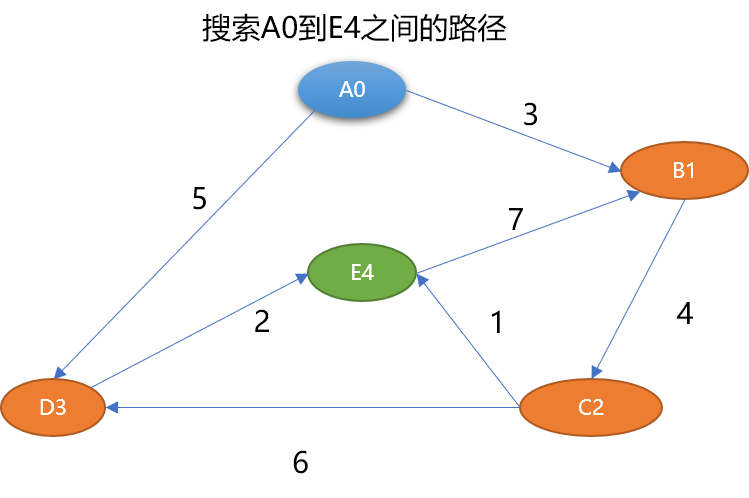
从人的直观思维角度查找一下，可以找到如下路径：

• {A0，B1，C2，E4}路径长度为 8。

• {A0，D3，E4} 路径长度为 7。

• {A0，B1，C2，D3，E4} 路径长度为 15。

在路径查找时，人的思维具有知识性和直观性特点，因此不存在所谓的尝试或碰壁问题。而计算机是试探性思维，就会出现这条路不通，再找另一条路的现象。

所以路径算法中常常会以错误为代价，在查找过程中会走一些弯路。常用的路径搜索算法有 2 种：

• 广度优先搜索

• 深度优先搜索

3.1 广度优先搜索

先看一下广度优先搜索的示意图：

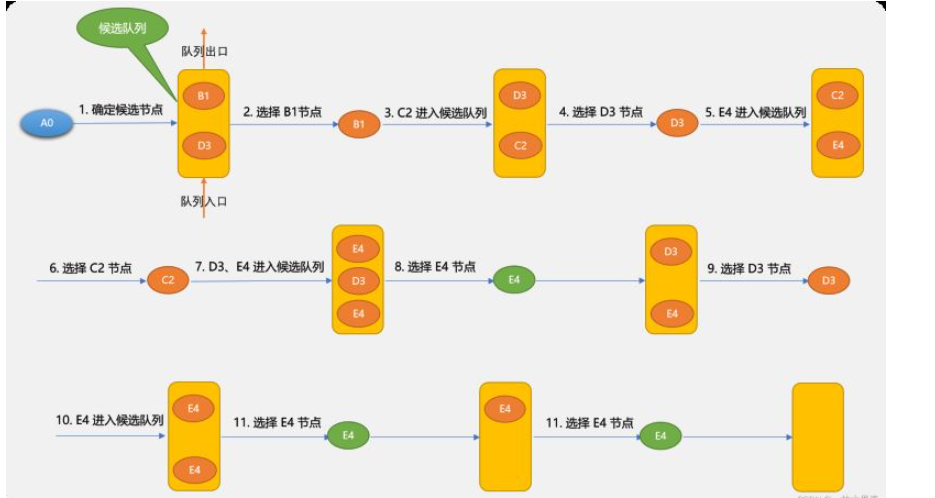
广度优先搜索的基本思路：

• 确定出发点，本案例是 A0 顶点。

• 以出发点相邻的顶点为候选点，并存储至队列。

• 从队列中每拿出一个顶点后，再把与此顶点相邻的其它顶点做为候选点存储于队列。

• 不停重复上述过程，至到找到目标顶点或队列为空。

使用广度搜索到的路径与候选节点进入队列的先后顺序有关系。如第 1 步确定候选节点时 B1 和 D3 谁先进入队列，对于后面的查找也会有影响。

上图使用广度搜索可找到 A0~E4 路径是：

{A0，B1，D3，C2，E4}

其实 {A0，B1，C2，E4} 也是一条有效路径，有可能搜索不出来，这里因为搜索到 B1 后不会马上搜索 C2，因为 B3 先于 C2 进入，广度优先搜索算法只能保证找到路径，而不能保存找到最佳路径。

编码实现广度优先搜索：

广度优先搜索需要借助队列临时存储选节点，本文使用列表模拟队列。

在图类中实现广度优先搜索算法的方法：

class Graph():
    
    # 省略其它代码

    '''
    广度优先搜索算法
    '''
    def bfs(self, from_v, to_v):
        # 查找与 fv 相邻的节点
        self.find_neighbor(from_v)
        # 临时路径
        lst_path = [from_v]
        # 重复条件：队列不为空
        while len(self.queue_stack) != 0:
            # 从队列中一个节点（模拟队列）
            tmp_v = self.queue_stack.pop(0)
            # 添加到列表中
            lst_path.append(tmp_v)
            # 是不是目标节点
            if tmp_v.v_id == to_v.v_id:
                self.searchPath.append(lst_path)
                print('找到一条路径', [v_.v_id for v_ in lst_path])
                lst_path.pop()
            else:
                self.find_neighbor(tmp_v)
    '''
    查找某一节点的相邻节点，并添加到队列（栈）中
    '''
    def find_neighbor(self, find_v):
        if find_v.visited:
            return
        find_v.visited = True
        # 找到保存 find_v 节点相邻节点的列表
        lst = self.matrix[find_v.v_id]
        for idx in range(len(lst)):
            if lst[idx] != 0:
                # 权重不为 0 ，可判断相邻
                self.queue_stack.append(self.vert_list[idx])

广度优先搜索过程中，需要随时获取与当前节点相邻的节点，find_neighbor() 方法的作用就是用来把当前节点的相邻节点压入队列中。

测试广度优先搜索算法：

if __name__ == "__main__":
    # 初始化图对象
    g = Graph(5)
    # 添加顶点
    for _ in range(len(g.matrix)):
        v_name = input("顶点的名称（ q 为退出）：")
        if v_name == 'q':
            break
        v = Vertex(v_name)
        g.add_vertex(v)

    # 节点之间的关系
    infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
    for i in infos:
        v = g.find_vertex(i[0])
        v1 = g.find_vertex(i[1])
        g.add_edge(v, v1, i[2])

    print("----------- 广度优先路径搜索--------------")
    f_v = g.find_vertex(0)
    t_v = g.find_vertex(4)
    g.bfs(f_v,t_v)
    '''
    输出结果
    顶点的名称（ q 为退出）：A
    顶点的名称（ q 为退出）：B
    顶点的名称（ q 为退出）：C
    顶点的名称（ q 为退出）：D
    顶点的名称（ q 为退出）：E


    ----------- 广度优先路径搜索--------------
    找到一条路径 [0, 1, 3, 2, 4]
    找到一条路径 [0, 1, 3, 2, 3, 4]
    '''

使用递归实现广度优先搜索算法：

   '''
    递归方式实现广度搜索
    '''
    def bfs_dg(self, from_v, to_v):
        self.searchPath.append(from_v)
        if from_v.v_id != to_v.v_id:
            self.find_neighbor(from_v)
        if len(self.queue_stack) != 0:
            self.bfs_dg(self.queue_stack.pop(0), to_v)

3.2 深度优先搜索算法

先看一下深度优先算法的示意图。

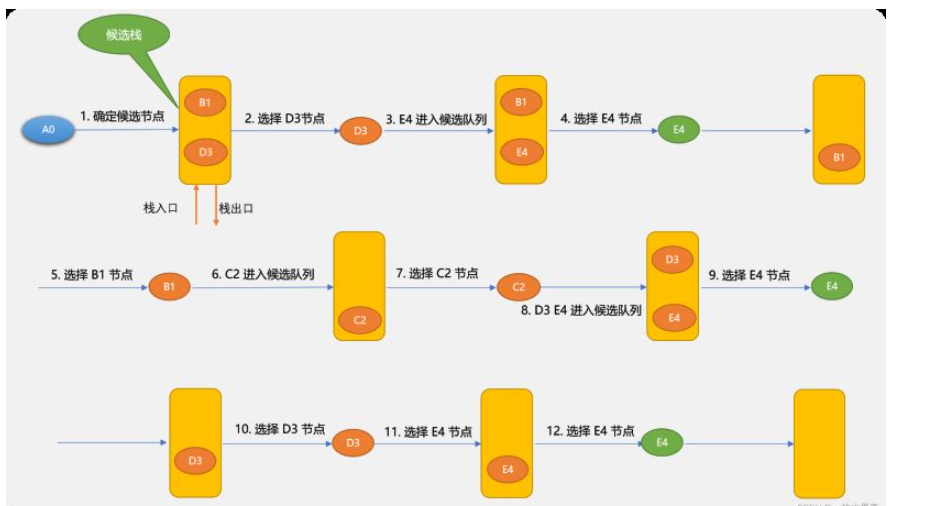
深度优先搜索算法和广度优先搜索算法不同的地方在于：深度优先搜索算法将候选节点放在堆栈中。因栈是先进后出，所以，搜索到的节点顺序不一样。

使用循环实现深度优先搜索算法：

深度优先搜索算法需要用到栈，本文使用列表模拟。

    '''
    深度优先搜索算法
    使用栈存储下一个需要查找的节点
    '''
    def dfs(self, from_v, to_v):
        # 查找与 from_v 相邻的节点
        self.find_neighbor(from_v)
        # 临时路径
        lst_path = [from_v]
        # 重复条件：栈不为空
        while len(self.queue_stack) != 0:
            # 从栈中取一个节点（模拟栈）
            tmp_v = self.queue_stack.pop()
            # 添加到列表中
            lst_path.append(tmp_v)
            # 是不是目标节点
            if tmp_v.v_id == to_v.v_id:
                self.searchPath.append(lst_path)
                print('找到一条路径:', [v_.v_id for v_ in lst_path])
                lst_path.pop()
            else:
                self.find_neighbor(tmp_v)

测试：

if __name__ == "__main__":
    # 初始化图对象
    g = Graph(5)
    # 添加顶点
    for _ in range(len(g.matrix)):
        v_name = input("顶点的名称（ q 为退出）：")
        if v_name == 'q':
            break
        v = Vertex(v_name)
        g.add_vertex(v)

    # 节点之间的关系
    infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
    for i in infos:
        v = g.find_vertex(i[0])
        v1 = g.find_vertex(i[1])
        g.add_edge(v, v1, i[2])
    # 输出顶点及边a
    print("-----------顶点与顶点关系--------------")
    g.find_vertexes()

    print("----------- 深度优先路径搜索--------------")
    f_v = g.find_vertex(0)
    t_v = g.find_vertex(4)
    g.dfs(f_v, t_v)
    '''
    输出结果
    顶点的名称（ q 为退出）：A
    顶点的名称（ q 为退出）：B
    顶点的名称（ q 为退出）：C
    顶点的名称（ q 为退出）：D
    顶点的名称（ q 为退出）：E
    -----------顶点与顶点关系--------------
[编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3
[编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5
[编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4
[编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6
[编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1
[编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2
[编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7
    ----------- 深度优先路径搜索--------------
    找到一条路径: [0, 3, 4]
    找到一条路径: [0, 3, 1, 2, 4]
    '''

使用递归实现深度优先搜索算法：

    '''
    递归实现深度搜索算法
    '''
    def def_dg(self, from_v, to_v):
        self.searchPath.append(from_v)
        if from_v.v_id != to_v.v_id:
            # 查找与 from_v 节点相连的子节点
            lst = self.find_neighbor_(from_v)
            if lst is not None:
                for tmp_v in lst[::-1]:
                    self.def_dg(tmp_v, to_v)
    """
    查找某一节点的相邻节点，以列表方式返回
    """
    def find_neighbor_(self, find_v):
        if find_v.visited:
            return
        find_v.visited = True
        # 查找与 find_v 节点相邻的节点
        lst = self.matrix[find_v.v_id]
        return [self.vert_list[idx] for idx in range(len(lst)) if lst[idx] != 0]

递归实现时，不需要使用全局栈，只需要获到当前节点的相邻节点便可。

Atas ialah kandungan terperinci Bagaimana untuk melaksanakan keluasan graf dan kedalaman algoritma carian laluan pertama dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!