 Peranti teknologi
Peranti teknologi
 AI
AI
 Bagaimanakah rantai pemikiran melepaskan keupayaan tersembunyi model bahasa? Penyelidikan teori terkini mendedahkan misteri di sebaliknya
Bagaimanakah rantai pemikiran melepaskan keupayaan tersembunyi model bahasa? Penyelidikan teori terkini mendedahkan misteri di sebaliknya
Bagaimanakah rantai pemikiran melepaskan keupayaan tersembunyi model bahasa? Penyelidikan teori terkini mendedahkan misteri di sebaliknya
Salah satu fenomena paling misteri dalam kemunculan model besar ialah Petua Rantaian Pemikiran (CoT), yang telah menunjukkan hasil yang menakjubkan dalam menyelesaikan masalah penaakulan matematik dan membuat keputusan. Betapa pentingnya CoT? Apakah mekanisme di sebalik kejayaannya? Dalam artikel ini, beberapa penyelidik dari Universiti Peking membuktikan bahawa CoT amat diperlukan dalam merealisasikan inferens model bahasa besar (LLM), dan mendedahkan cara CoT boleh mengeluarkan potensi besar LLM dari perspektif teori dan eksperimen.
Penyelidikan terkini mendapati bahawa Rangkaian Pemikiran (CoT) boleh meningkatkan prestasi model bahasa besar (LLM) dengan ketara, terutamanya untuk memproses masalah kompleks yang melibatkan matematik atau penaakulan. Tetapi walaupun banyak kejayaan, mekanisme di sebalik CoT dan cara membuka kunci potensi LLM masih sukar difahami.
Baru-baru ini, satu kajian baharu dari Universiti Peking mendedahkan misteri di sebalik CoT dari perspektif teori.

Pautan kertas: https://arxiv.org/abs/2305.15408
Model bahasa besar berasaskan pengubah telah menjadi model biasa dalam pemprosesan bahasa semula jadi dan telah digunakan secara meluas dalam pelbagai tugas. Model besar arus perdana biasanya dilaksanakan berdasarkan paradigma autoregresif Secara khusus, pelbagai tugas (seperti terjemahan teks, penjanaan teks, menjawab soalan, dll.) boleh dianggap secara seragam sebagai masalah penjanaan urutan, di mana input soalan dan penerangan. daripada soalan dikodkan bersama-sama ke dalam urutan perkataan (token), dipanggil prompt (prompt);

Sebilangan besar kajian dalam bidang model besar telah menunjukkan bahawa reka bentuk yang baik kata-kata gesaan Memainkan peranan penting dalam prestasi model. Terutama apabila ia berkaitan dengan aritmetik atau tugas yang berkaitan dengan penaakulan, CoT telah ditunjukkan untuk meningkatkan dengan ketara ketepatan jawapan yang dijana. Seperti yang ditunjukkan dalam rajah di bawah, untuk tugasan yang memerlukan penaakulan matematik, jawapan yang dijana secara langsung oleh model besar selalunya salah (angka a,b di bawah). Walau bagaimanapun, jika anda mengubah suai gesaan supaya model besar mengeluarkan keseluruhan rantaian pemikiran (langkah derivasi perantaraan), anda akhirnya akan dapat jawapan yang betul (c, d di bawah).

Dalam amalan, terdapat dua cara arus perdana untuk melaksanakan gesaan rantaian pemikiran: satu ialah menambah Frasa tertentu seperti " Mari kita fikir langkah demi langkah" dicetuskan (seperti ditunjukkan dalam c di atas); yang lain adalah untuk menyediakan sebilangan kecil contoh demonstrasi rantai pemikiran untuk membolehkan model besar mensimulasikan proses terbitan yang sepadan (seperti ditunjukkan dalam d di atas).
Walau bagaimanapun, walaupun CoT telah mencapai prestasi yang luar biasa dalam sebilangan besar eksperimen, mekanisme teori di sebaliknya kekal sebagai misteri. Di satu pihak, adakah model besar sememangnya mempunyai kelemahan teori yang wujud dalam menjawab soalan secara langsung tentang matematik, penaakulan, dsb.? Sebaliknya, mengapakah CoT boleh meningkatkan keupayaan model besar pada tugasan ini? Kertas kerja ini menjawab soalan di atas dari perspektif teori.
Khususnya, penyelidik mengkaji CoT dari perspektif kebolehan ekspresi model: Untuk tugasan matematik dan tugasan membuat keputusan am, kertas kerja ini mengkaji model Transformer berdasarkan autoregresi dalam dua keupayaan Ekspresif berikut dari segi: (1) menjana jawapan secara langsung, dan (2) menggunakan CoT untuk menjana langkah penyelesaian yang lengkap.
CoT ialah kunci untuk menyelesaikan masalah matematik
Model besar yang diwakili oleh GPT-4 telah menunjukkan keupayaan matematik yang menakjubkan. Contohnya, ia boleh menyelesaikan kebanyakan masalah matematik sekolah menengah dengan betul dan juga telah menjadi pembantu penyelidik untuk ahli matematik.
Untuk mengkaji keupayaan matematik model besar, artikel ini memilih dua tugasan matematik yang sangat asas tetapi teras: aritmetik dan persamaan (rajah berikut menunjukkan input kedua-dua contoh output tugasan ini ). Oleh kerana ia adalah komponen asas untuk menyelesaikan masalah matematik yang kompleks, dengan mengkaji dua masalah matematik teras ini, kita boleh memperoleh pemahaman yang lebih mendalam tentang keupayaan model besar mengenai masalah matematik umum.

Para penyelidik mula-mula meneroka sama ada Transformer boleh mengeluarkan jawapan kepada soalan di atas tanpa mengeluarkan langkah perantaraan. Mereka menganggap andaian yang sangat konsisten dengan realiti - Transformer ketepatan log, iaitu, setiap neuron Transformer hanya boleh mewakili nombor titik terapung ketepatan terhad (ketepatan ialah log n bit), di mana n ialah panjang maksimum daripada ayat tersebut. Andaian ini sangat hampir dengan realiti, contohnya dalam GPT-3, ketepatan mesin (16 atau 32 bit) biasanya jauh lebih kecil daripada panjang ayat output maksimum (2048).
Di bawah andaian ini, penyelidik membuktikan hasil teras yang mustahil: Untuk model Transformer autoregresif dengan lapisan malar dan lebar d, untuk mengeluarkan secara langsung Jawapannya ialah apabila menyelesaikan dua masalah matematik di atas, lebar model yang sangat besar d perlu digunakan. Secara khusus, d perlu berkembang lebih besar daripada polinomial apabila panjang input n bertambah.
Sebab penting untuk keputusan ini ialah tiada algoritma selari yang cekap untuk dua masalah di atas, jadi Transformer, sebagai model selari biasa, tidak dapat menyelesaikannya. Artikel ini menggunakan teori kerumitan litar dalam sains komputer teori untuk membuktikan dengan teliti teorem di atas.
Jadi, bagaimana jika model tidak mengeluarkan jawapan secara langsung, tetapi mengeluarkan langkah-langkah terbitan perantaraan dalam bentuk rajah di atas? Para penyelidik seterusnya membuktikan melalui pembinaan bahawa apabila model boleh mengeluarkan langkah perantaraan, model Transformer autoregresif dengan saiz tetap (tidak bergantung pada panjang input n) boleh menyelesaikan dua masalah matematik di atas.
Membandingkan keputusan sebelumnya, dapat dilihat bahawa penambahan CoT sangat meningkatkan keupayaan ekspresi model besar. Para penyelidik seterusnya memberikan pemahaman intuitif tentang perkara ini: Ini kerana pengenalan CoT akan terus menyuap semula perkataan output yang dijana ke lapisan input, yang meningkatkan kedalaman berkesan model, menjadikannya berkadar dengan panjang output CoT, sekali gus meningkatkan kecekapan model Kerumitan selari Transformer telah bertambah baik.
CoT ialah kunci untuk menyelesaikan masalah umum membuat keputusan
Selain masalah matematik, penyelidik mempertimbangkan lagi keupayaan CoT untuk menyelesaikan tugasan umum. Bermula dari masalah membuat keputusan, mereka menganggap rangka kerja umum untuk menyelesaikan masalah membuat keputusan, yang dipanggil pengaturcaraan dinamik.
Idea asas pengaturcaraan dinamik (DP) adalah untuk menguraikan masalah yang kompleks kepada satu siri sub-masalah berskala kecil yang boleh diselesaikan mengikut turutan. Penguraian masalah memastikan wujud perkaitan (tindih) yang ketara antara pelbagai sub-masalah, supaya setiap sub-masalah dapat diselesaikan dengan cekap menggunakan jawapan kepada sub-masalah sebelumnya.
Jujukan menaik terpanjang (LIS) dan menyelesaikan jarak suntingan (ED) ialah dua masalah DP terkenal yang dicadangkan dalam buku "Pengenalan kepada Algoritma" Jadual berikut menyenaraikan fungsi Pengagregatan ini nyatakan ruang, fungsi peralihan untuk dua masalah.

Para penyelidik membuktikan bahawa model Transformer autoregresif boleh menyelesaikan sub-masalah seperti berikut Urutan mengeluarkan rantai pemikiran pengaturcaraan dinamik yang lengkap, supaya jawapan yang betul boleh dikeluarkan untuk semua tugas yang boleh diselesaikan dengan pengaturcaraan dinamik. Begitu juga, penyelidik seterusnya menunjukkan bahawa rantai pemikiran generatif adalah perlu: untuk banyak masalah pengaturcaraan dinamik yang sukar, model Transformer bersaiz polinomial lapisan malar tidak boleh mengeluarkan jawapan yang betul secara langsung. Artikel itu memberikan contoh balas kepada masalah ujian keahlian tatabahasa tanpa konteks.
Eksperimen
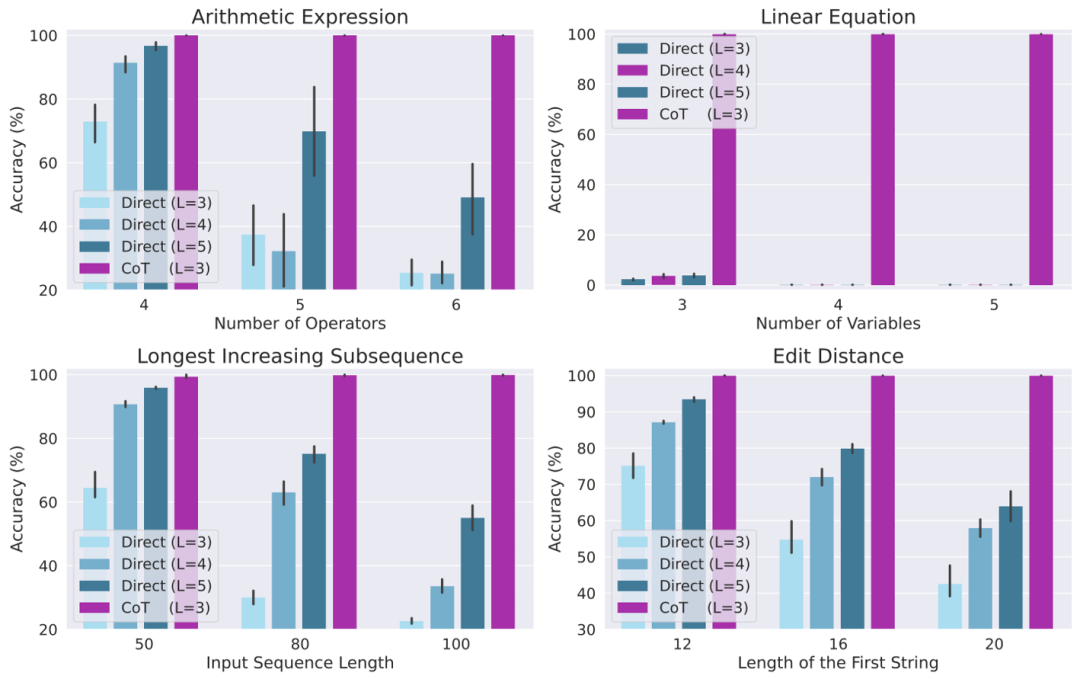
Penyelidik akhirnya mereka bentuk sebilangan besar eksperimen untuk mengesahkan teori di atas, dengan mengambil kira empat tugas yang berbeza: menilai ungkapan aritmetik, menyelesaikan persamaan linear, dan menyelesaikan urutan naik terpanjang dan menyelesaikan jarak suntingan.
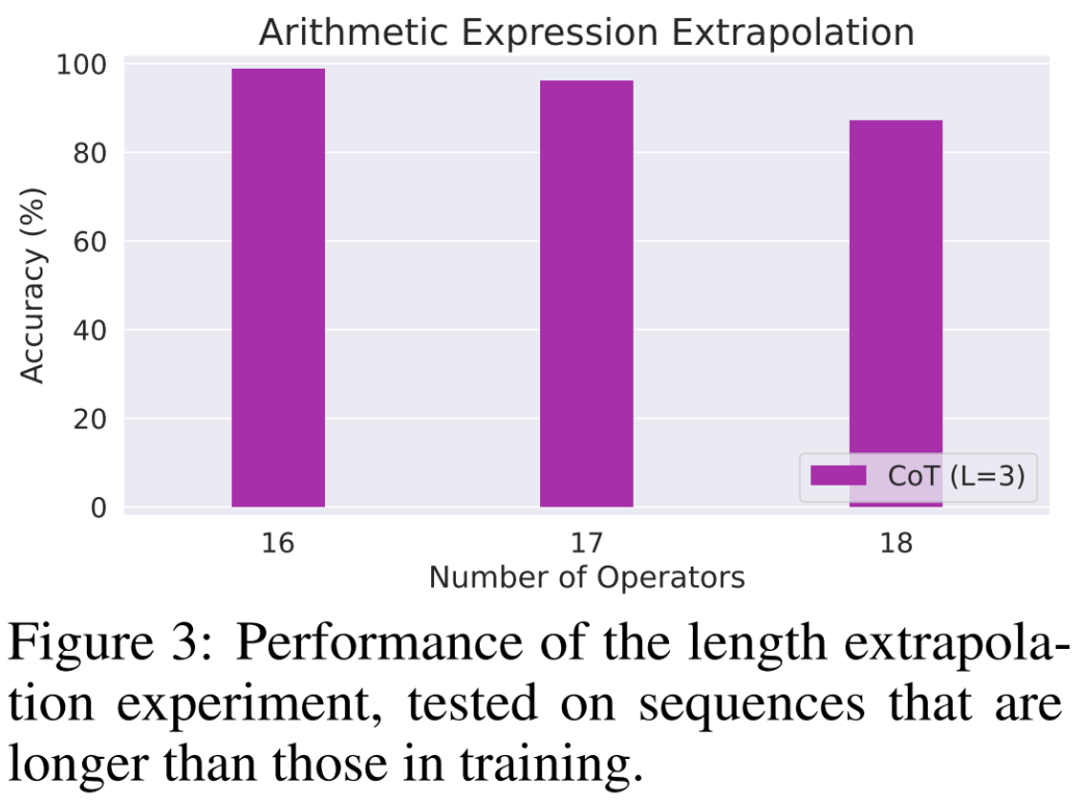
Hasil eksperimen menunjukkan bahawa apabila dilatih menggunakan data CoT, model Transformer autoregresif 3 lapisan telah dapat mencapai prestasi yang hampir sempurna pada semua tugas. Walau bagaimanapun, secara langsung mengeluarkan jawapan yang betul menunjukkan prestasi yang buruk pada semua tugas (walaupun dengan model yang lebih mendalam). Keputusan ini jelas menunjukkan keupayaan Autoregressive Transformer untuk menyelesaikan pelbagai tugas yang kompleks dan menunjukkan kepentingan CoT dalam menyelesaikan tugasan ini.
Atas ialah kandungan terperinci Bagaimanakah rantai pemikiran melepaskan keupayaan tersembunyi model bahasa? Penyelidikan teori terkini mendedahkan misteri di sebaliknya. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Model MoE sumber terbuka paling berkuasa di dunia ada di sini, dengan keupayaan bahasa Cina setanding dengan GPT-4, dan harganya hanya hampir satu peratus daripada GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Model MoE sumber terbuka paling berkuasa di dunia ada di sini, dengan keupayaan bahasa Cina setanding dengan GPT-4, dan harganya hanya hampir satu peratus daripada GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Bayangkan model kecerdasan buatan yang bukan sahaja mempunyai keupayaan untuk mengatasi pengkomputeran tradisional, tetapi juga mencapai prestasi yang lebih cekap pada kos yang lebih rendah. Ini bukan fiksyen sains, DeepSeek-V2[1], model MoE sumber terbuka paling berkuasa di dunia ada di sini. DeepSeek-V2 ialah gabungan model bahasa pakar (MoE) yang berkuasa dengan ciri-ciri latihan ekonomi dan inferens yang cekap. Ia terdiri daripada 236B parameter, 21B daripadanya digunakan untuk mengaktifkan setiap penanda. Berbanding dengan DeepSeek67B, DeepSeek-V2 mempunyai prestasi yang lebih kukuh, sambil menjimatkan 42.5% kos latihan, mengurangkan cache KV sebanyak 93.3% dan meningkatkan daya pemprosesan penjanaan maksimum kepada 5.76 kali. DeepSeek ialah sebuah syarikat yang meneroka kecerdasan buatan am
 Apr 09, 2024 am 11:52 AM
Apr 09, 2024 am 11:52 AM
AI memang mengubah matematik. Baru-baru ini, Tao Zhexuan, yang telah mengambil perhatian terhadap isu ini, telah memajukan keluaran terbaru "Buletin Persatuan Matematik Amerika" (Buletin Persatuan Matematik Amerika). Memfokuskan pada topik "Adakah mesin akan mengubah matematik?", ramai ahli matematik menyatakan pendapat mereka Seluruh proses itu penuh dengan percikan api, tegar dan menarik. Penulis mempunyai barisan yang kuat, termasuk pemenang Fields Medal Akshay Venkatesh, ahli matematik China Zheng Lejun, saintis komputer NYU Ernest Davis dan ramai lagi sarjana terkenal dalam industri. Dunia AI telah berubah secara mendadak Anda tahu, banyak artikel ini telah dihantar setahun yang lalu.
 Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Prestasi JAX, yang dipromosikan oleh Google, telah mengatasi Pytorch dan TensorFlow dalam ujian penanda aras baru-baru ini, menduduki tempat pertama dalam 7 penunjuk. Dan ujian tidak dilakukan pada TPU dengan prestasi JAX terbaik. Walaupun dalam kalangan pembangun, Pytorch masih lebih popular daripada Tensorflow. Tetapi pada masa hadapan, mungkin lebih banyak model besar akan dilatih dan dijalankan berdasarkan platform JAX. Model Baru-baru ini, pasukan Keras menanda aras tiga hujung belakang (TensorFlow, JAX, PyTorch) dengan pelaksanaan PyTorch asli dan Keras2 dengan TensorFlow. Pertama, mereka memilih satu set arus perdana
 Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas secara rasmi memasuki era robot elektrik! Semalam, Atlas hidraulik hanya "menangis" menarik diri daripada peringkat sejarah Hari ini, Boston Dynamics mengumumkan bahawa Atlas elektrik sedang berfungsi. Nampaknya dalam bidang robot humanoid komersial, Boston Dynamics berazam untuk bersaing dengan Tesla. Selepas video baharu itu dikeluarkan, ia telah pun ditonton oleh lebih sejuta orang dalam masa sepuluh jam sahaja. Orang lama pergi dan peranan baru muncul. Ini adalah keperluan sejarah. Tidak dinafikan bahawa tahun ini adalah tahun letupan robot humanoid. Netizen mengulas: Kemajuan robot telah menjadikan majlis pembukaan tahun ini kelihatan seperti manusia, dan tahap kebebasan adalah jauh lebih besar daripada manusia Tetapi adakah ini benar-benar bukan filem seram? Pada permulaan video, Atlas berbaring dengan tenang di atas tanah, seolah-olah terlentang. Apa yang berikut adalah rahang-jatuh
 KAN, yang menggantikan MLP, telah diperluaskan kepada konvolusi oleh projek sumber terbuka
Jun 01, 2024 pm 10:03 PM
KAN, yang menggantikan MLP, telah diperluaskan kepada konvolusi oleh projek sumber terbuka
Jun 01, 2024 pm 10:03 PM
Awal bulan ini, penyelidik dari MIT dan institusi lain mencadangkan alternatif yang sangat menjanjikan kepada MLP - KAN. KAN mengatasi MLP dari segi ketepatan dan kebolehtafsiran. Dan ia boleh mengatasi prestasi MLP berjalan dengan bilangan parameter yang lebih besar dengan bilangan parameter yang sangat kecil. Sebagai contoh, penulis menyatakan bahawa mereka menggunakan KAN untuk menghasilkan semula keputusan DeepMind dengan rangkaian yang lebih kecil dan tahap automasi yang lebih tinggi. Khususnya, MLP DeepMind mempunyai kira-kira 300,000 parameter, manakala KAN hanya mempunyai kira-kira 200 parameter. KAN mempunyai asas matematik yang kukuh seperti MLP berdasarkan teorem penghampiran universal, manakala KAN berdasarkan teorem perwakilan Kolmogorov-Arnold. Seperti yang ditunjukkan dalam rajah di bawah, KAN telah
 Robot Tesla bekerja di kilang, Musk: Tahap kebebasan tangan akan mencapai 22 tahun ini!
May 06, 2024 pm 04:13 PM
Robot Tesla bekerja di kilang, Musk: Tahap kebebasan tangan akan mencapai 22 tahun ini!
May 06, 2024 pm 04:13 PM
Video terbaru robot Tesla Optimus dikeluarkan, dan ia sudah boleh berfungsi di kilang. Pada kelajuan biasa, ia mengisih bateri (bateri 4680 Tesla) seperti ini: Pegawai itu juga mengeluarkan rupanya pada kelajuan 20x - pada "stesen kerja" kecil, memilih dan memilih dan memilih: Kali ini ia dikeluarkan Salah satu sorotan video itu ialah Optimus menyelesaikan kerja ini di kilang, sepenuhnya secara autonomi, tanpa campur tangan manusia sepanjang proses. Dan dari perspektif Optimus, ia juga boleh mengambil dan meletakkan bateri yang bengkok, memfokuskan pada pembetulan ralat automatik: Berkenaan tangan Optimus, saintis NVIDIA Jim Fan memberikan penilaian yang tinggi: Tangan Optimus adalah robot lima jari di dunia paling cerdik. Tangannya bukan sahaja boleh disentuh
 FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: algoritma pengesanan sasaran pertama berdasarkan kamera fisheye
Apr 26, 2024 am 11:37 AM
Pengesanan objek ialah masalah yang agak matang dalam sistem pemanduan autonomi, antaranya pengesanan pejalan kaki adalah salah satu algoritma terawal untuk digunakan. Penyelidikan yang sangat komprehensif telah dijalankan dalam kebanyakan kertas kerja. Walau bagaimanapun, persepsi jarak menggunakan kamera fisheye untuk pandangan sekeliling agak kurang dikaji. Disebabkan herotan jejari yang besar, perwakilan kotak sempadan standard sukar dilaksanakan dalam kamera fisheye. Untuk mengurangkan perihalan di atas, kami meneroka kotak sempadan lanjutan, elips dan reka bentuk poligon am ke dalam perwakilan kutub/sudut dan mentakrifkan metrik mIOU pembahagian contoh untuk menganalisis perwakilan ini. Model fisheyeDetNet yang dicadangkan dengan bentuk poligon mengatasi model lain dan pada masa yang sama mencapai 49.5% mAP pada set data kamera fisheye Valeo untuk pemanduan autonomi
 DualBEV: mengatasi BEVFormer dan BEVDet4D dengan ketara, buka buku!
Mar 21, 2024 pm 05:21 PM
DualBEV: mengatasi BEVFormer dan BEVDet4D dengan ketara, buka buku!
Mar 21, 2024 pm 05:21 PM
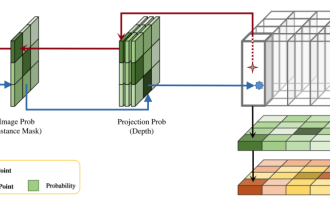
Kertas kerja ini meneroka masalah mengesan objek dengan tepat dari sudut pandangan yang berbeza (seperti perspektif dan pandangan mata burung) dalam pemanduan autonomi, terutamanya cara mengubah ciri dari perspektif (PV) kepada ruang pandangan mata burung (BEV) dengan berkesan dilaksanakan melalui modul Transformasi Visual (VT). Kaedah sedia ada secara amnya dibahagikan kepada dua strategi: penukaran 2D kepada 3D dan 3D kepada 2D. Kaedah 2D-ke-3D meningkatkan ciri 2D yang padat dengan meramalkan kebarangkalian kedalaman, tetapi ketidakpastian yang wujud dalam ramalan kedalaman, terutamanya di kawasan yang jauh, mungkin menimbulkan ketidaktepatan. Manakala kaedah 3D ke 2D biasanya menggunakan pertanyaan 3D untuk mencuba ciri 2D dan mempelajari berat perhatian bagi kesesuaian antara ciri 3D dan 2D melalui Transformer, yang meningkatkan masa pengiraan dan penggunaan.





