Dia mahu mengelakkan peperiksaan 70 tahun lalu, tetapi dia mempengaruhi seluruh Internet

Siapa sangka "kesediaan" pelajar tidak mahu mengambil peperiksaan nanti akan menjejaskan keseluruhan Internet.

Dalam kelas teori maklumat di MIT 70 tahun yang lalu, seorang guru mengemukakan soalan aneka pilihan untuk "mengurangkan" tekanan pelajar.

Sama ada ambil peperiksaan akhir atau tulis kertas kerja untuk menambah baik algoritma sedia ada, pilihan anda.

Nama guru itu ialah Robert Fanno Apa yang dia tidak beritahu pelajar ialah "algoritma sedia ada" ini betul-betul Shannon-Fanno pengekodan yang dia tulis bersama Shannon, pengasas teori maklumat. Untuk memperbaiki kelemahan algoritma, dia sendiri telah melabur banyak masa dalam penyelidikan.

(OS dalaman guru: Saya tidak menjangkakannya.)

Walaupun ia agak merosakkan, helah ini benar-benar berkesan. Kumpulan pelajar ini tidak perlu mengambil peperiksaan sebaik sahaja mereka mendengar "tangan dalam kertas" dan memutuskan untuk menulis kertas dengan segera, termasuk David Huffman.

Anda tidak akan tahu jika anda tidak memilih, tetapi anda akan terkejut jika anda memilih. Huffman, yang baru bermula, dengan cepat menyedari perangkap yang telah digali oleh guru - kertas ini terlalu sukar untuk diselesaikan.

Ia mengambil masa beberapa bulan untuk menulis ini, dan walaupun bekerja keras, Huffman masih tidak mendapat apa-apa.

Tapi takdir sangat pelik kadang-kadang. Hanya apabila Huffman akhirnya menyerah "ponteng peperiksaan" dan hendak membuang nota kertas ke dalam tong sampah, dia tiba-tiba mendapat idea! Jawapannya muncul!

Huffman meninggalkan penyelidikan tentang pengekodan sedia ada dan beralih kepada penerokaan baharu, dan akhirnya menemui kaedah berdasarkan pengekodan pokok perduaan kekerapan yang dipesan.

Kecekapan idea yang dicadangkannya ini berjaya mengatasi metodologi gurunya. Malah dalam perkembangan seterusnya, kaedah pengekodan yang dinamakan sempena namanya - Pengekodan Huffman, secara langsung mengubah paradigma mampatan data.

Bagi laporan akhir pada masa itu, ia telah dipetik hampir 10,000 kali.

Kaedah pengekodan tradisional yang tidak cekap

Pada tahun 1951, Robert Fanno, yang mengajar di MIT, memikirkan masalah sukar dalam teori maklumat:

Bagaimana menggunakan kod binari dengan cekap untuk mewakili nombor, huruf atau simbol lain?

Kaedah yang paling biasa dan langsung pada masa itu adalah untuk menetapkan nombor binari yang unik kepada setiap aksara.

Sebagai contoh, huruf A boleh diwakili sebagai 01000001,! Diwakili sebagai 00100001, setiap nombor lapan digit sepadan dengan satu aksara.

Ini menjadikan kod mudah dihuraikan, tetapi kecekapannya sangat rendah.

Terdapat juga kaedah pengoptimuman, serupa dengan kod Morse. Huruf biasa E diwakili oleh hanya satu titik, tetapi Q yang tidak biasa memerlukan "————··——” yang lebih panjang dan susah payah.

Kaedah ini akan membawa kepada panjang kod yang berbeza dan maklumat tidak mudah difahami dan jurang perlu ditambah antara aksara semasa penghantaran, jika tidak, kombinasi aksara yang berbeza tidak dapat dibezakan.

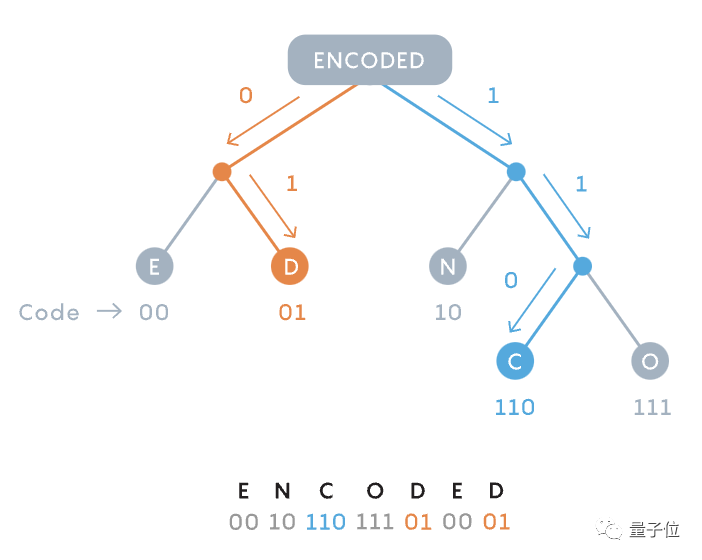
Fanno menyedari bahawa mungkin kelebihan kedua-dua kaedah ini boleh digabungkan - mewakili aksara dalam kod binari dengan panjang yang berbeza. Tambahan pula, untuk mengelakkan kod "bertindih", dia juga membina pokok binari.

Gambar

Dia menguji secara menyeluruh kemungkinan setiap pilihatur untuk kecekapan maksimum, dan akhirnya mendapat situasi yang berkesan:

Setiap mesej dibahagikan kepada dua cabang mengikut kekerapan, dan seberapa banyak yang mungkin Biarkan kekerapan penggunaan huruf pada kedua-dua belah pada asasnya adalah sama.

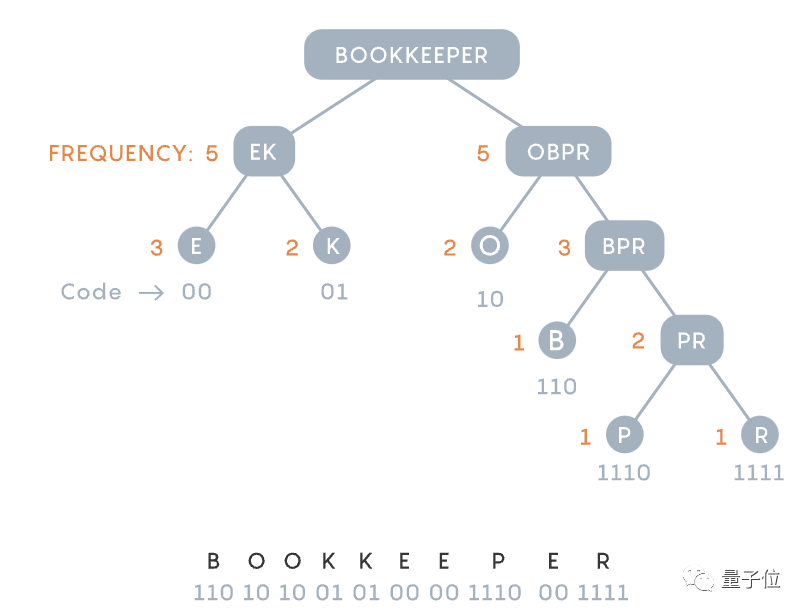Gambar

Dengan cara ini, aksara yang biasa digunakan akan berada pada dahan yang lebih pendek dan kurang padat.

Pada tahun 1948, Shannon, bapa teori maklumat, mencadangkan kaedah ini dalam artikel "Teori Komunikasi Matematik" yang memperkenalkan teori maklumat tidak lama kemudian, Fanno juga menerbitkannya secara bebas dalam bentuk laporan teknikal. Oleh itu, kaedah ini dipanggil

Shannon-Fano coding.

Tetapi kaedah ini tidak selalu berkesan. Sebagai contoh, apabila kebarangkalian kejadian huruf ialah {0.35, 0.17, 0.17, 0.16, 0.15}, pengekodan yang ideal tidak boleh diberikan.

Fano percaya bahawa mesti ada strategi pemampatan yang lebih baik. Sejak itu, tugas penting itu diletakkan di tangan pelajarnya.

Sekitar inspirasi, kertas abad ini

Jika ada, kaedah Profesor Fanno ialah membina pokok watak dari atas ke bawah dan mengekalkan simetri sebanyak mungkin antara pasangan dahan.

Kemudian kaedah Huffman secara langsung mematahkan proses ini -

Bina pokok binari dari bawah ke atas.

Dia percaya bahawa, tidak kira apa yang berlaku, dalam sekeping kod yang sah,

dua aksara yang paling kurang biasa harus mempunyai dua kod terpanjang.

Jadi mula-mula kenal pasti dua aksara yang paling kurang biasa, gabungkan mereka bersama-sama sebagai pasangan cawangan, dan kemudian ulangi proses untuk mencari aksara yang paling kurang biasa daripada aksara yang tinggal dan pasangan aksara yang baru dibina (pasangan ).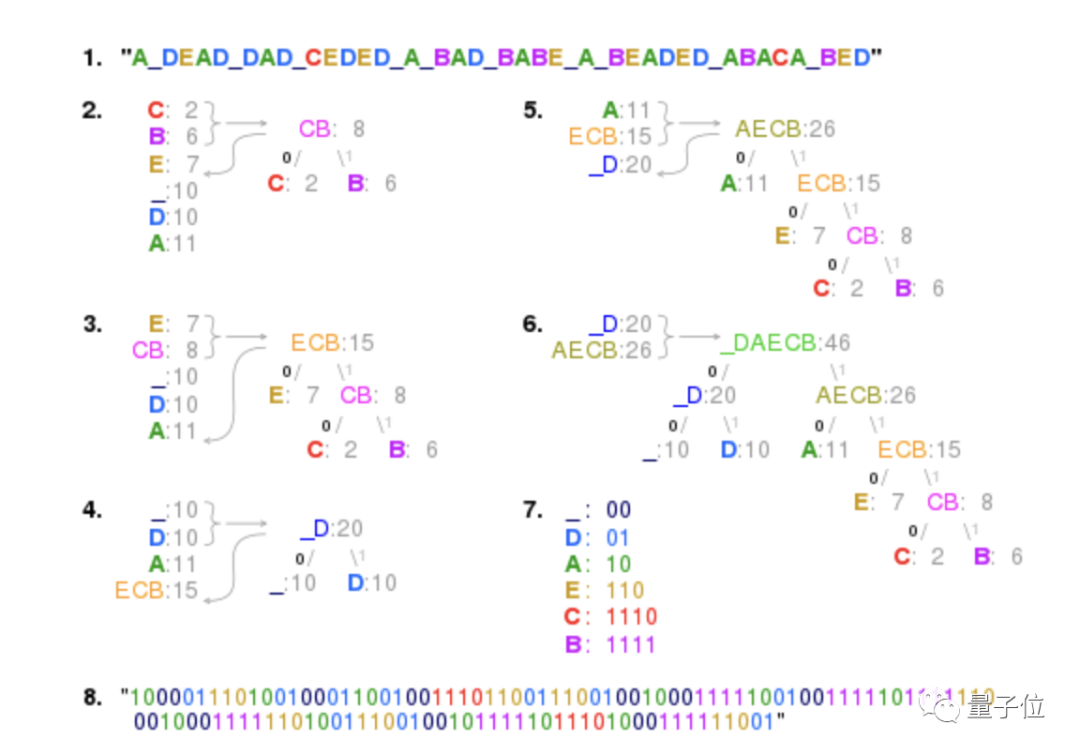

Gambar

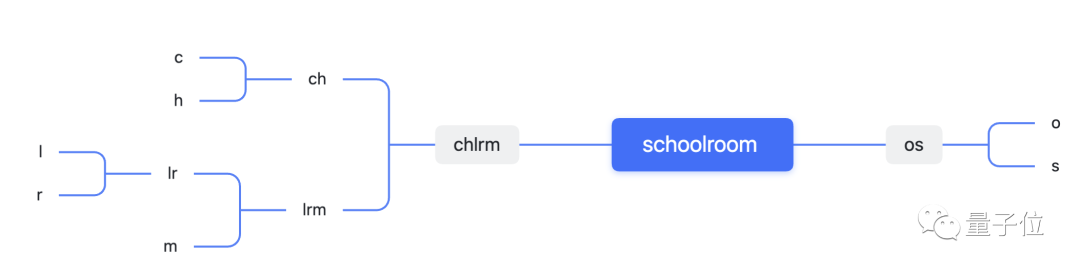
Ambil bilik sekolah sebagai contoh, di mana O muncul empat kali, dan S, C, H, L, R dan M muncul sekali setiap satu.

Kaedah Fano adalah untuk menetapkan O dan satu lagi huruf dahulu ke cawangan kiri, supaya kedua-dua belah mempunyai jumlah penggunaan sebanyak 5 kali, dan kod yang dihasilkan berjumlah 27 bit.

Gambar

Sebaliknya, kaedah Huffman, sebagai contoh, bermula daripada r dan m yang tidak lazim dan menggabungkannya menjadi pasangan huruf.

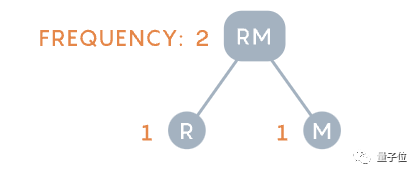Gambar

Selepas digabungkan, aksara sedia ada (berpasangan) termasuk: O (4 kali), RM (2 kali) dan huruf tunggal S, C, H dan L.

Bahagikan mengikut kekerapan kejadian, ulangi operasi sebelumnya - kumpulkan dua pilihan yang tidak biasa, dan kemudian kemas kini pepohon nombor dan rajah kekerapan.

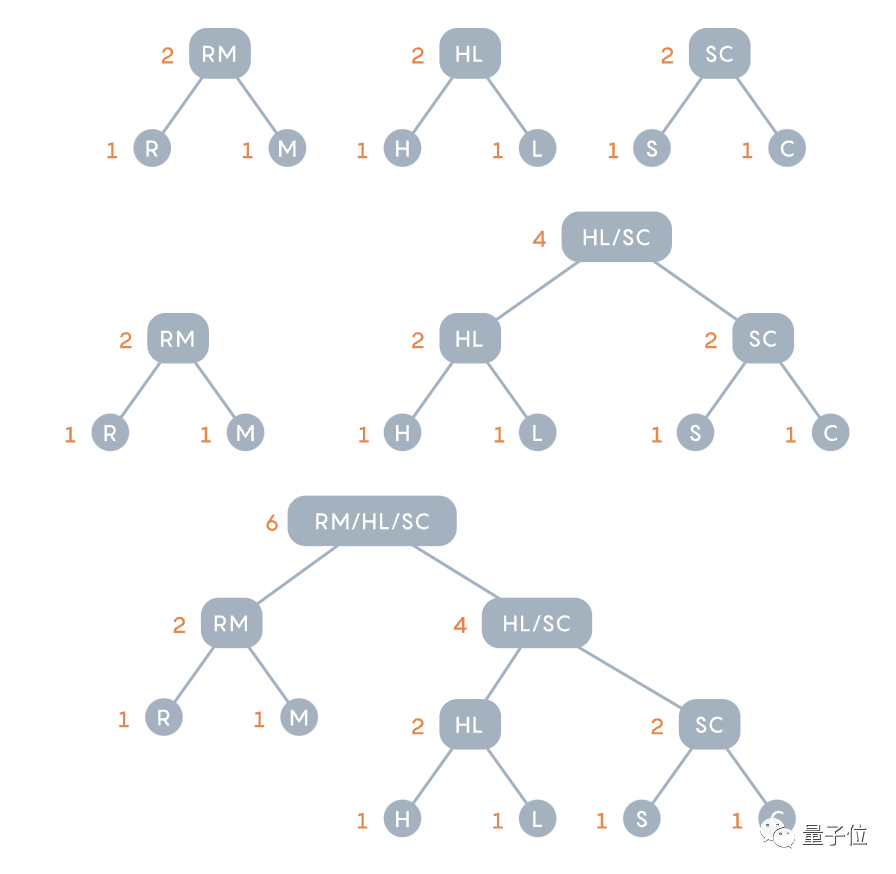
Akhirnya, "bilik sekolah" menjadi 11101111110000110110000101, iaitu 1 sedikit kurang daripada pendekatan atas ke bawah Fano.

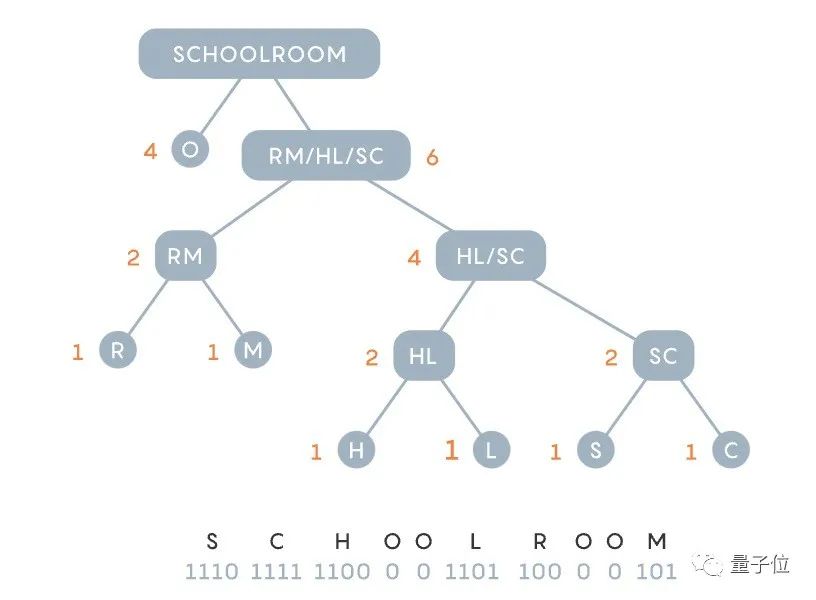Gambar

Walaupun 1 bit tidak banyak di sini, apabila dikembangkan kepada berbilion bait, ini adalah penjimatan yang besar.

Malah, kaedah Huffman telah terbukti sangat berkuasa Menurut statistik Google Scholar, kertas pada tahun itu telah dipetik sebanyak 9570 kali.

Gambar

Bagi kaedah gurunya, hampir tidak pernah digunakan lagi.

Sehingga hari ini, hampir semua kaedah pemampatan tanpa kerugian menggunakan kaedah Huffman secara keseluruhan atau sebahagian, yang boleh memampatkan imej, audio, jadual, dll. Ia menyokong segala-galanya daripada standard imej PNG kepada perisian PKZip yang ada di mana-mana.

Knuth, perintis sains komputer moden dan pemenang Anugerah Turing, pernah menggambarkan pencapaian Huffman dengan cara ini:

Dalam bidang sains komputer dan komunikasi data, pengekodan Huffman ialah idea asas yang digunakan oleh orang ramai.

Kemudian, Huffman teringat detik "eureka" ketika itu, dia hendak membuang nota kertas ke dalam tong sampah, tetapi tiba-tiba fikirannya datang bersama-sama, dan jawapannya muncul di fikirannya:

Itulah yang paling pelik. perkara dalam detik hidup saya.

Makrifat secara tiba-tiba, seperti kilat.

Dan menyatakan bahawa jika dia tahu bahawa profesornya Fano telah bergelut dengan masalah ini, dia mungkin tidak pernah cuba menyelesaikannya, apatah lagi mengambil risiko pada usia 25 tahun.

Rasa pencapaian dan pesanan, bermain seni dengan matematik

Pengekodan Huffman mengubah paradigma pemampatan data dan memenangi banyak penghormatan dan pingat.

Sebagai contoh, Huffman memenangi Anugerah Jubli Emas untuk Inovasi Teknikal daripada Persatuan Teori Maklumat IEEE pada tahun 1998, dan Pingat Richard Hamming dari Institut Jurutera Elektrik dan Elektronik (IEEE) pada tahun 1999.

Namun begitu, dalam perjalanan hidupnya, berbanding dengan ciptaan kaedah pemampatan lossless, apa yang paling dibanggakannya ialah tesis kedoktoran ini.

Tajuk: Sintesis Litar Pensuisan Berjujukan.

Picture

Semasa Huffman belajar untuk PhD di MIT, dia menerbitkan kertas kerja penting ini membincangkan litar pensuisan berjujukan. Pada masa itu, Huffman hampir merupakan sarjana pertama yang menerangkan cara mereka bentuk litar pensuisan berjujukan tak segerak, dan teori ini kemudiannya memberikan sokongan logik yang penting untuk pembangunan komputer. Penerbitan kertas kerja ini bukan sahaja membantunya memperoleh Pingat Louis E. Levy daripada Institut Franklin, tetapi juga secara semulajadi membolehkannya memperoleh kelayakan untuk kekal di sekolah dan mengajar kursus mengenai litar pensuisan.

GambarSemasa di sekolah, Huffman juga mencadangkan formula matematik inovatif yang boleh menukar

jujukan nombor binari kepada satu lagi urutan nombor binari

tanpa kehilangan sebarang maklumat dan telah memainkan peranan penting pada masa itu jawatan penting.

William O. Baker, kemudian Naib Presiden Penyelidikan di Bell Labs, merekrutnya ke jawatankuasa semakan yang bertanggungjawab terutamanya untuk menyemak rancangan teknologi masa depan untuk Agensi Keselamatan Negara. Dr. Baker berkhidmat sebagai penasihat saintifik kepada lima presiden: Eisenhower, Kennedy, Johnson, Nixon, dan Reagan.

Hoffman, yang sudah menjadi profesor penuh pada tahun 1967, memilih untuk meninggalkan MIT dan menyertai Universiti California, Santa Cruz (UCSC) Dalam tempoh ini, beliau mengetuai penubuhan Jabatan Sains Komputer dan mengambil bahagian dalam pembangunan kursus akademik, meletakkan asas penting untuk pembangunan seterusnya Jabatan Sains Komputer.

Matematik boleh dikatakan sebagai salah satu usaha sepanjang hayat Huffman, sehinggakan apabila dia kemudiannya terlibat dalam seni, dia tidak boleh melakukannya tanpa matematik.

Gambar

Bermula pada tahun 1970-an, Huffman mula berminat dengan origami pada masa yang sama mempelajari matematik dan seni origami, menghasilkan ratusan karya origami melengkung, dan menerbitkan kertas kerja secara khusus analisis mathematik. . , menjadi perintis dalam bidang matematik origami.

Mengimbas kembali, Huffman telah memenangi pelbagai penghormatan dan pujian sepanjang hayatnya, tetapi dia tidak pernah memohon paten untuk mana-mana ciptaannya.

Akhirnya, izinkan saya meminjam petikan daripada Huffman sendiri.

Sebagai seorang saintis dan guru, saya memang gigih. Jika saya merasakan bahawa saya tidak menemui penyelesaian yang paling mudah untuk masalah, saya menjadi sangat tidak berpuas hati, dan rasa tidak puas hati ini akan berterusan sehingga saya menemui penyelesaian yang terbaik. Bagi saya, inilah intipati menjadi seorang saintis.

Atas ialah kandungan terperinci Dia mahu mengelakkan peperiksaan 70 tahun lalu, tetapi dia mempengaruhi seluruh Internet. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!